数列探索性问题分类和对应解题思路分析
2022-09-03黄保球
黄保球
(江苏省清江中学)
数列问题是高中数学重要的考查题型,主要包含求数列的通项、数列求和以及以数列为载体的综合问题.近年来,数列相关的探索性问题考查频率在逐渐提升,要求学生在掌握数列基础知识的前提下求解相关探索性问题,具有一定的综合性和难度.本文主要介绍三类不同的数列探索问题:条件探索性问题、结论探索性问题、存在性探索问题,并结合例题对不同类型问题的方法和思路进行分析.
1 条件探索性问题
与数列相关的条件探索性问题常常会给出确切的结论,要求考生对满足结论的条件进行分析和探索,运用分析法解题的关键在于从结论着手找出必要条件.解答条件探索类数列问题,具体的解题思路如下:
1)根据问题给出的结论得到相关必要条件,结合已知条件将必要条件转化为具体的关系式;
2)结合题意,给关系式添加限制条件,求解关系式,即可得到使结论成立的条件.
例1已知数列{an}为等差数列,a1=2,{an}的前n项和为Sn,数列{bn}为等比数列,且a1b1+a2b2+…+anbn=(n-1)2n+2+4对任意n∈N*恒成立.
(1)求数列{an},{bn}的通项公式;
(2)各项均为正整数的无穷等差数列{cn}满足c39=a1007,且存在正整数k使c1,c39,ck成等比数列.若数列{cn}的公差为d,求d的所有可能取值之和.
分析聚焦第(2)问,首先问题给出已经成立的结论:c1,c39,ck为等比数列,由该结论可推导出必要条件.结合第(1)问的通项公式和条件c39=a1007可求出c1,c39,ck的表达式,将其代入必要条件得到具体等式.结合题意给等式添加限制条件,此时可求得充分条件d的值,进而求出d的所有可能取值之和.
解(1)an=2n,bn=2n(求解过程略).
(2)当d=0时,符合题意.
当d>0,由c39=c1+38d=2014,可得
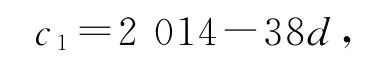
ck=c39+(k-39)d=2014+(k-39)d,将c1,ck带入中,可得
(2014-38d)[2014+(k-39)d]=20142,化简得kd-39d=53k-53×77,则
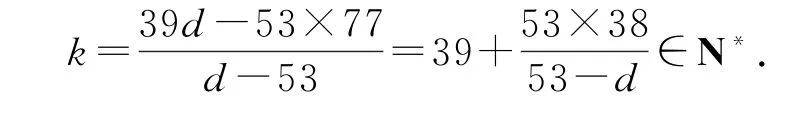
又因为c1=2014-38d=38(53-d)>0,d>0,所以d=34,51,52,故d的所有可能取值之和为137.
变式已知数列{an}是首项为a,公差为1的等差数列,若对任意n∈N*都有bn≥b8成立,则实数a的取值范围为_________.
分析首先对结论bn≥b8进行分析,结合{an}是递增数列且公差为1,可得与a有关的不等式组,求出的范围即为a的取值范围.
解因为,若对任意n∈N*都有bn≥b8,即bn-b8≥0,则,又因为{an}是递增数列且公差为1,所以a9>0且a8<0,所以解得-8<a<-7.
综上,实数a的取值范围为(-8,-7).
2 结论探索性问题
与数列有关的结论探索性问题主要是根据具体的条件推导具体结论或判断所给结论的正误,解答这类问题可采取特例法,即从特殊情况着手分析、探索得到结论后,验证一般情况下该结论成立与否.求解数列的结论探索性问题,解题思路通常如下:
1)对问题题意进行分析,根据已知条件对结论进行猜想;
2)通过数列求通项和前n项和的运算方法,判断猜想的结论正确;
3)证明猜想结论.
例2已知各项均为正数的数列{an}满足,且a2+a4=2a3+4,其 中n∈N*.
(1)求数列{an}的通项公式;
分析主要对第(2)问进行分析,要比较Tn和2的大小关系,首先凭借第(1)问{an}的通项公式,求出数列{cn}的通项公式,分析通项公式的结构特点,采取错位相减法求解Tn的表达式为.易得到Tn<2的大小关系,故猜想结论Tn<2,证明过程即对应整个推理过程.
解(1)an=2n(求解过程略).
(2)结论为Tn<2,证明过程如下.

3 存在性探索问题
存在性探索问题是指在已知条件下对与数列有关的某一参数或某一结论成立存在的可能性进行探索,通常运用反证法进行解答,即假设问题给出的结论成立,在该前提下进行逻辑推理,若推断过程中存在矛盾,则假设不成立,反之则可得到存在的对应具体值.解答数列的存在性探索问题,常见的解题思路如下:
1)假设问题中需要探索的存在性条件或结论成立,得到对应的关系等式;
2)结合已知条件,对推导得到的关系等式进行验证;
3)若验证过程中存在矛盾,对应的假设不成立,该条件或结论不存在;反之,若无矛盾之处,则假设成立.
例3设数列{an}的前n项和为Sn,且Sn=n2,数列{bn}满足),是否存在m使得数列{bn}中某项bt满足b1,b4,bt(t∈N*,t≥5)成为等差数列? 若存在,写出符合题意的m的个数;若不存在,说明理由.
分析问题对参数m的存在性进行探索,解题时要先求出an,bn的通项公式,假设存在m使得数列{bn}中b1,b4,bt(t∈N*,t≥5)成等差数列这一结论成立,则2b4=b1+bt,根据已知条件求出b1,b4,bt的具体表达式,并代入2b4=b1+bt中,判断等式是否成立.若成立,则可求得参数m的具体个数,此时应结合m∈N,t∈N*,t≥5进行判断,求出符合结论的m的个数.
解因为Sn=n2,Sn-1=(n-1)2,所以当n≥2时,有an=Sn-Sn-1=2n-1.
又因为当n=1时,a1=S1=1符合an=2n-1,即{an}的通项公式为an=2n-1,所以
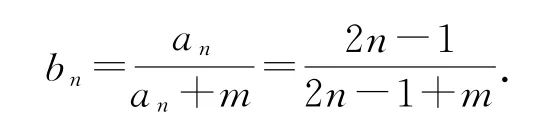
由题意得2b4=b1+bt,则
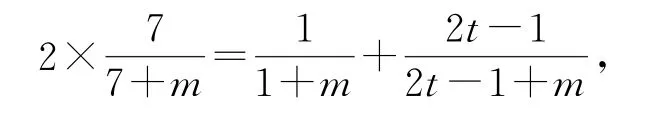
综上,当m=6,7,8,9,11,14,17,23,41时,存在t=43,25,19,16,13,11,10,9,8 满足题意,即存在m∈N 使得b1,b4,bt(t∈N*,t≥5)成等差数列,满足题意的m有9个.
数列探索性问题的考查具有一定的意义,不仅要求学生熟练掌握并运用数列求通项以及数列求和方法,还要求学生具有一定的逻辑思维和创新能力.分析上述三类数列探索性问题不难发现,不同类型问题对应不同的解题策略和思路,学生应熟悉和掌握这些内容,才能灵活运用不同方法解题.
(完)
