寻找同型，同构函数，利用共性

孟美金

(山东省青岛西海岸新区第二高级中学)

同构意识是破解数学问题比较常见的一种解题意识,特别是在解决一些比较复杂的等式或不等式问题时,可以结合关系式结构特征对等式或不等式进行变形与转化,合理同构函数,再利用函数的基本性质解题.

1 地位同等要同构

含有地位同等的两个变量x1,x2或x,y的等式或不等式,如果进行恒等变形与整理后,等式或不等式两边具有关系式结构特征的一致性,往往可以巧妙同构函数,应用函数的基本性质(单调性、奇偶性等)分析与解决.

例1若cos5θ－sin5θ＜7(sin3θ－cos3θ),θ∈[0,2π),则θ的取值范围是_________.

根据题目条件,结合三角不等式进行“同名”变形、合理移项处理,找到不等号两边的同型结构,进而构造函数,利用所构造函数的奇偶性与单调性,巧妙转化三角不等式,再利用三角函数中的辅助角公式以及三角函数的图像与性质确定θ的取值范围.

因为cos5θ＋7cos3θ＜sin5θ＋7sin3θ,设f(x)＝x5＋7x3,则f(x)是R 上的奇函数且单调递增,所以不等式f(cosθ)＜f(sinθ)等价于cosθ＜sinθ,即sinθ－cosθ＞0,整理可得,解得,结合θ∈[0,2π),可得

利用地位同等策略构造函数时,往往需要对题目条件中的等式或不等式以同名、同次、同级别、同类型等形式加以恒等变形转化,使得等号或不等号两边关系式的结构特征相一致,进而合理构造函数,借助同一函数的共性分析与处理问题.

变式若2x－2y＜3－x－3－y,则( ).

对2x－2y＜3－x－3－y移项变形得2x－3－x＜2y－3－y,设f(x)＝2x－3－x,因为y＝2x,y＝－3－x单调递增,所以f(x)是定义在R 上的增函数,故由2x－3－x＜2y－3－y,得x＜y,所以yx＞0,即y－x＋1＞1,从而ln(y－x＋1)＞0,故选A.

2 指对(数)跨阶同构

涉及指数式与对数式混合的等式或不等式,往往需要跨阶转化与处理,均转化为类指数函数型或类对数函数型,进而巧妙同构一个函数,这个函数需要满足指对跨阶、单调性和最值易求等,从而实现跨阶同构解决问题.

例2若实数x1,x2满足x1ex1＝e3,x2(lnx2－2)＝e5,那么x1x2＝_____.

根据题目条件,要求解x1x2,就要考虑将两个等式加以统一结构化处理,可以化对数式为指数式,也可以化指数式为对数式,进而巧妙同构函数求解.

方法1由实数x1,x2满足x1ex1＝e3,x2(lnx2－2)＝e5,可得x1＞0,x2＞e2.

设lnx2－2＝t＞0,则有lnx2＝t＋2,将对数式转化为指数式可得x2＝et＋2,代入x2(lnx2－2)＝e5,并整理可得tet＝e3.

设f(x)＝xex(x＞0),则f′(x)＝(x＋1)ex＞0(x＞0),所以f(x)在(0,＋∞)上单调递增,而f(x1)＝f(t)＝e3,可得x1＝t＝lnx2－2,所以

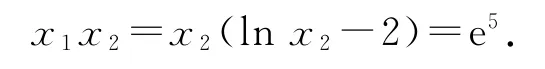
方法2对x1ex1＝e3两边同时取自然对数,可得lnx1＋x1＝3,对x2(lnx2－2)＝e5两边同时取自然对数得

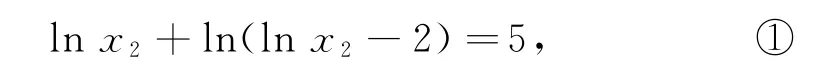
为使两式结构特征相同,将①进一步变形为

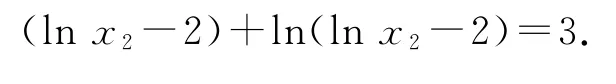
设f(x)＝lnx＋x(x＞0),则0,所以f(x)在(0,＋∞)上单调递增,则方程f(x)＝3的解只有一个,可得x1＝lnx2－2,所以x1x2＝(lnx2－2)x2＝e5.

在解决一些涉及指数、对数三阶的综合问题时,往往可以通过等式或不等式的恒等变形转化,借助指对(数)跨阶函数的同构,将原问题转化为同一个函数背景下的问题进行求解.

变式已知x0是方程x3ex－4＋2lnx－4＝0的一个根,那么的值是( ).

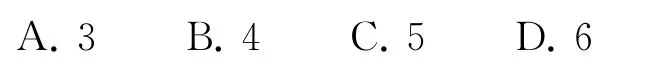
由x3ex－4＋2lnx－4＝0,配凑可得

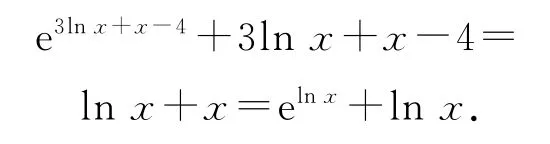
设f(x)＝ex＋x,则f′(x)＝ex＋1＞0恒成立,故函数f(x)在R上单调递增.

由f(3lnx＋x－4)＝f(lnx),可得

故选B.

3 无中生有去同构

若题目条件中的一些相关式子无法直接进行变形与巧妙同构,往往需要通过配凑常数、参数或变量(如同时乘x或同时加x)等,构建指对(数)跨阶形式,进而巧妙解决问题.

例3若2a＋log2a＝4b＋2log4b,则( ).

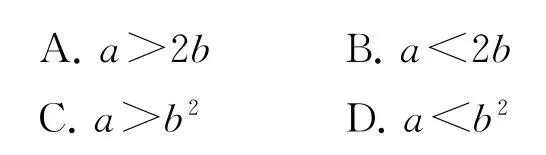
根据题目条件,对等式中等号两边相应的关系式进行结构特征一致化变形处理.借助常数进行“无中生有”,从而巧妙放缩处理,化等式为不等式,借助同构函数的单调性确定相关函数所对应变量间的大小关系.

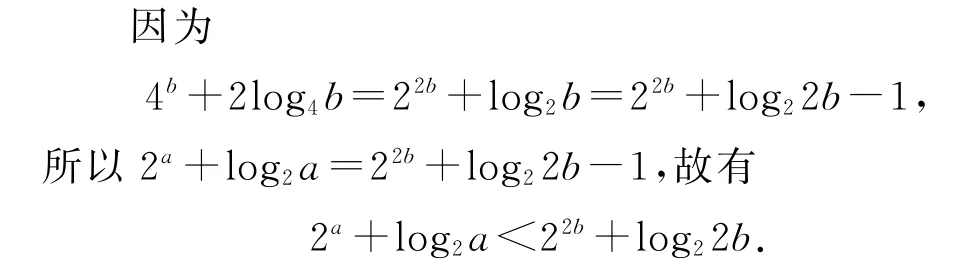
设f(x)＝2x＋log2x(x＞0),则函数f(x)在(0,＋∞)上为增函数,所以由f(a)＜f(2b),可得a＜2b.而

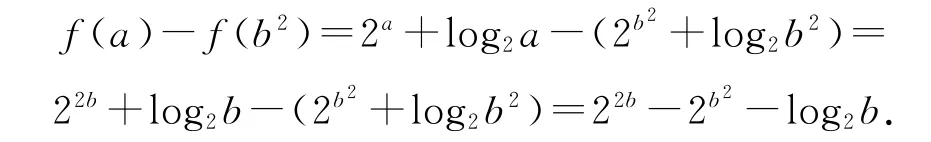
当b＝1时,f(a)－f(b2)＝2＞0,此时f(a)＞f(b2),则a＞b2.

当b＝2时,f(a)－f(b2)＝－1＜0,此时f(a)＜f(b2),则a＜b2,故选B.

为了利用地位同等或指对(数)跨阶策略同构函数,进而利用同构函数的共性求解问题,经常采用放缩变形,通过配凑常数、参数或变量等方式进行结构特征一致化处理,从而使等号或不等号两边函数类型相同.

变式若asina－4bsinbcosb＝4b2－a2＋1,则( ).

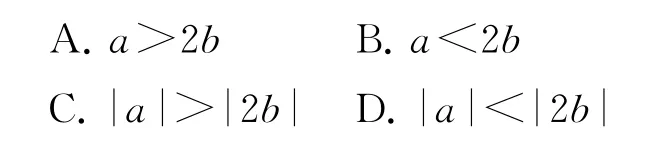
由asina－2bsin 2b＝4b2－a2＋1,可得asina＋a2＝4b2＋2bsin2b＋1,则有asina＋a2＝(2b)2＋2bsin2b＋1＞(2b)2＋2bsin2b.

设f(x)＝xsinx＋x2,因为f(－x)＝－xsin(－x)＋(－x)2＝f(x),所以f(x)为偶函数,求导可得

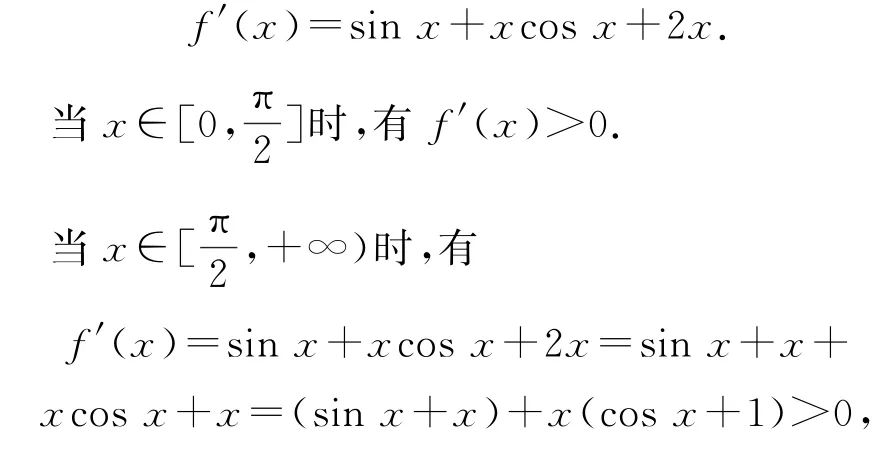
所以当x≥0时,f′(x)＞0,函数f(x)在[0,＋∞)上为增函数,由asina＋a2＞(2b)2＋2bsin2b,可得f(a)＞f(2b).

又由于f(x)为偶函数,则f(|a|)≥f(|2b|),所以|a|＞|2b|,故选C.

在破解一些数学问题时,“寻同型找共性”,需借助我们的慧眼去识别问题中的代数式或不等式等结构特征的相似之处,通过不断感知、抽象、认同、同构、建模等过程,链接题中涉及知识与所学知识的密切联系,将不熟悉的问题转化为熟悉的问题处理,不断增强创新意识、同构意识与创新应用.

(完)