函数零点与导数的完美邂逅

于广续

(山东省济南市章丘中学)

函数的零点问题是函数的重要内容之一,通过导数的学习,不难发现,利用导数工具来研究函数的零点是常用的方法,该类试题不仅能够较好地考查学生的数学核心素养,还能够较好地考查学生的运算求解能力和转化与化归能力,因此受到命题者的青睐.

1 证明函数的零点个数

例1已知函数f(x)＝xlnx－4x,g(x)＝

(1)求函数f(x)的最小值;

(2)证明:函数h(x)＝f(x)＋g(x)仅有一个零点.

解析(1)函数f(x)的定义域为(0,＋∞),且f′(x)＝lnx－3.

当0＜x＜e3时,f′(x)＜0,函数f(x)在(0,e3)上单调递减;当x＞e3时,f′(x)＞0,函数f(x)在(e3,＋∞)上单调递增,所以

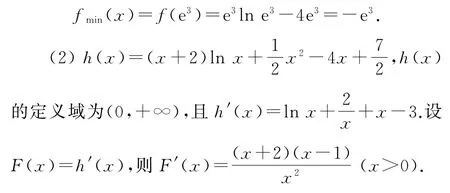
当0＜x＜1时,F′(x)＜0;当x＞1时,F′(x)＞0,即函数F(x)在(0,1)上单调递减,在(1,＋∞)上单调递增,所以当x＞0时,F(x)≥F(1)＝0(当且仅当x＝1时取等号),即当x＞0时,h′(x)≥0(当且仅当x＝1时取等号),所以函数h(x)在(0,＋∞)上单调递增,h(x)至多有一个零点.

因为h(1)＝0,则x＝1 是函数h(x)唯一的零点,所以函数h(x)＝f(x)＋g(x)仅有一个零点.

点评函数零点个数的判定与证明主要通过三种方法进行处理,一是直接求解f(x)＝0,该方程的解的个数即为零点的个数;二是图像法,通过函数的图像,观察图像与x轴交点的个数或是转化为两个函数图像,观察两个函数图像的交点个数;三是利用零点存在定理进行判定,也可结合最值、极值进行处理.

2 零点偏移问题

例2已知函数)在点(1,f(1))处的切线方程与x轴平行.

(1)求函数f(x)的极值;

(2)若函数g(x)＝f(x)－k有两个不同的零点x1,x2.

(ⅰ)求k的取值范围;

(ⅱ)证明:x1x2＜1.

解析(1),f′(1)＝,故a＝0,,当0＜x＜1时,f′(x)＜0;当x＞1时,f′(x)＞0,故f(x)在(0,1)上单调递减,在(1,＋∞)上单调递增,故f(x)在x＝1处有极小值f(1)＝e,无极大值.

(2)(ⅰ)g(x)＝f(x)－k有两个零点等价于h(x)＝ex－kx有两个零点,又h′(x)＝ex－k,当k≤1时,h′(x)＝ex－k＞0在R 上恒成立,所以h(x)在R 上单调递增,不可能有两个零点.

当k＞1 时,令h′(x)＞0,解得x＞lnk;令h′(x)＜0,解得0＜x＜lnk,所以h(x)在(0,lnk)上单调递减,在(lnk,＋∞)上单调递增.

因为函数h(x)＝ex－kx有两个零点,所以h(lnk)＜0,k＞1,所以elnk－klnk＜0,解得k＞e.

令h(k)＝ek－k2,h′(k)＝ek－2k,h″(k)＝ek－2,所以h′(k)在(e,＋∞)上单调递增,故h′(k)＞h′(e)＝ee－2e＞0,故h(k)在(e,＋∞)上单调递增,故h(k)＝ek－k2＞ee－e2＞0,故h(x)在(1,k)上存在唯一零点.

综上,k的取值范围为k＞e.

点评解决此类问题的关键在于消参,常见的消参方法是对所给式子进行变形,然后引入新的变量,此目的在于减少变量的个数,进而构建新的函数,通过研究新函数的单调性求解问题.

3 隐零点问题

例3若函数f(x)＝axex(a∈R).

(1)当a＜0时,求函数f(x)的单调区间;

(2)设b为实数,若不等式f(x)≥2x2＋bx对任意的a≥1及任意的x＞0恒成立,求b的取值范围;

(3)若函数g(x)＝f(x)＋x＋lnx(x＞0)有两个相异的零点,求a的取值范围.

解析(1)函数f(x)的单调递增区间为(－∞,－1),单调递减区间为(－1,＋∞).

(2)b≥2－2ln2(求解过程略).

(3)由g(x)＝axex＋x＋lnx,得g′(x)＝,其中x＞0.

当a≥0时,g′(x)＞0,函数g(x)在(0,＋∞)上单调递增,函数g(x)至多有一个零点,不符合题意.

当a＜0时,令g′(x)＝0,得,求导可知,当x＞0时,ex－2x≥2－2ln2＞0,所以ex＞2x,则xex＞2x2,所以当x＞0时,函数xex的值域为(0,＋∞),所以存在x0＞0,使得ax0ex0＋1＝0,即

当x＜x0时,g′(x)＞0,当x＞x0时,g′(x)＜0,所以函数g(x)在(0,x0)上单调递增,在(x0,＋∞)上单调递减.

因为函数g(x)有两个零点x1,x2,所以

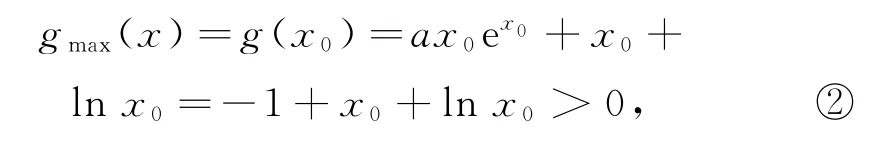
设φ(x)＝－1＋x＋lnx(x＞0),则0,所以φ(x)在(0,＋∞)上单调递增,由于φ(1)＝0,所以当x＞1时,φ(x)＞0,所以式②中的x0＞1.

点评导数是研究函数的有力工具,其核心是由导数值的正、负确定函数的单调性.用导数研究函数f(x)的单调性,往往需要解方程f′(x)＝0.若该方程不易求解,这就是隐零点问题,这类问题的解决关键是要明确所研究函数的零点所在的区间.

(完)