函数图像及性质在解题中的应用

董梦茹

(山东省邹平市第一中学)

函数图像及性质是高考中的重要考点.部分习题较为抽象,解题需要运用一定的技巧.为提高学生的解题能力,教师应结合近年来高考常考题型,为学生讲解函数图像及性质在解题中的具体应用,进一步深化学生对函数图像及性质的理解,促使其积累不同题型的解题经验与技巧,促进其解题能力的提升.

1 比较数值大小

解答该类习题主要运用函数的单调性,部分问题还会涉及函数的奇偶性、对称性等,当题目中给出的函数为抽象函数时往往还需要学生结合题干已知条件构造新的函数,判断函数的单调性.

例1已知f(x)是定义在(0,＋∞)上的减函数,其导函数为f′(x).若,则下列不等式成立的是( ).

解析该题涉及的函数为抽象函数,具有一定的难度.解题时应认真观察,冷静分析.因题干中涉及导函数,因此可考虑构造函数.

2 确定零点个数

函数零点问题是近年来高考的热点,主要考查学生运用数形结合思想求解问题的能力.解答该类问题首先应明确零点表示的含义,能够根据已知条件对零点问题进行合理转化,化陌生为熟悉,如将复杂函数进行拆分,将零点问题转化成函数图像交点问题.同时,在绘制函数图像时应注重把握两个细节:其一,明确不同定义域内函数的表达式;其二,能够结合题干条件绘制准确的函数图像.

例2已知函数f(x)的定义域为R,且满足f(1＋x)＝f(x－1),当x∈[－1,1]时,f(x)＝1－则函数h(x)＝f(x)－g(x)在区间[－5,5]内的零点个数为( ).

解析题目仅给出了f(x)在[－1,1]上的表达式,需要研究其周期.分段函数给出的函数较为常见,不难画出其图像,因此,解题时可在同一直角坐标系中画出f(x)和g(x)的函数图像,再观察其在[－5,5]内的交点个数即可.

因为f(1＋x)＝f(x－1),所以将x换为x＋1,可得f(x＋2)＝f(x),所以f(x)的周期为2.画出两个函数的图像,如图1所示.

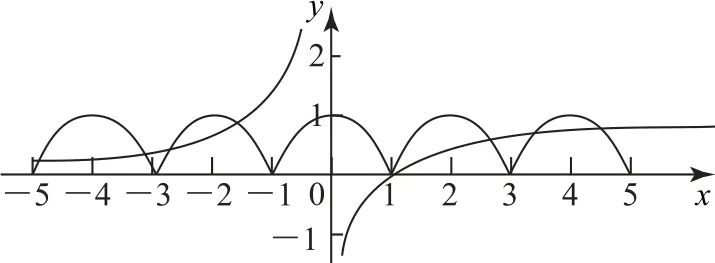
图1

由函数图像可以清晰地看到两个函数图像在[－5,5]内的交点个数为8,因此,函数h(x)的零点个数为8,故选B.

3 解不等式

不等式是高考的必考知识点.问题类型多样且灵活多变,难度也存在较大差别,解题时应注重联系函数性质,充分挖掘题干隐含条件,对要求解的问题进行合理转化.同时,运用函数的单调性、对称性等性质,化复杂为简单.

例3已知f(x)＝ex－1－e1－x＋(x－1)3＋x是定义在R 上的函数,则不等式f(x－4)＋f(2－3x)≥2的解集为( ).

A.(－∞,－2] B.(－∞,2]

C.[－2,2] D.[2,＋∞)

解析根据经验需要借助函数的奇偶性、对称性以及单调性,将比较函数值的大小问题转化为比较函数自变量的大小问题.

令t＝x－1,则f(t)＝et－e－t＋t3＋t＋1,令g(t)＝et－e－t＋t3＋t,显然其为单调递增的奇函数,则f(x)关于点(1,1)对称,满足f(2－x)＋f(x)＝2,又因为f(x－4)＋f(2－3x)≥2,所以f(x－4)≥2－f(2－3x)＝f(3x),即x－4≥3x,解得x≤－2,故选A.

4 求解函数值

该类问题要求学生求解较大自变量的函数值或求多个函数值之和,解答该类题一般不要直接将自变量的值代入,应充分运用已知条件找到函数的周期,借助函数的周期性进行解答.

例4已知f(x)是定义在R 上的奇函数,且满足f(x)＝f(2－x),当x∈[0,1]时,f(x)＝4x－1,则的值为( ).

解析题目仅给出了当x∈[0,1]时函数f(x)的解析式,而并不在该定义域中,因此,需要根据已知条件“f(x)＝f(2－x)”推导出函数的周期性.

因为f(x)＝f(2－x),所以将x换成x＋2可得f(x＋2)＝f(－x)＝－f(x).再将x换成x＋2可得f(x＋4)＝－f(x＋2)＝f(x),则f(x)的周期为4,所以,又x∈[0,1]时,f(x)＝4x－1,则,故选C.

5 求解参数的范围

求解参数的范围是高中数学的热门考点,问题情境复杂多变.该类问题常常要转化为求解函数的最值问题.需要注意的是该类问题中的恒成立与存在性问题之间的区别与联系,避免将两个问题混淆,确定求解问题是求最大值还是最小值.

例5若关于x的不等式在[2,4]上有解,则实数m的取值范围是( ).

解析需要注意的是该题属于存在性问题,分离变量后应注重求解对应函数的最大值而非最小值.运用导数研究函数的单调性时,若求导后无法判断导函数与零的关系,需再次构造函数,直到能够判断出函数在给定区间的单调性为止.

6 小结

高中数学函数图像以及性质内容较多,教师既要鼓励学生积极动手画出常见的函数图像,进一步加深其印象,又要鼓励学生推导、总结函数的单调性、奇偶性、周期性以及对称性的数学表达式,真正吃透函数性质,进而在解题中能够从已知条件中迅速地判断出函数的性质.另外,针对较为复杂的函数,应注重提高导数应用意识,借助导数判断其单调性,力求高效、顺利地求解相关问题.

(完)