加强代数推理 发展理性思维——以“有理数的乘法（1）”的教学为例

陈世文，张宗余

（浙江师范大学附属嘉善实验学校；浙江省教育厅教研室）

《义务教育数学课程标准（2022年版）》（以下简称《标准》）指出，数与代数领域的学习，有助于学生形成抽象能力、推理能力和模型观念，发展几何直观与运算能力.特别强调，在“数与代数”的教学中要加强推理能力的培养，理解逻辑推理在形成数学概念、法则、定理和解决问题中的重要性，初步掌握推理的基本形式和规则；对于一些简单问题，能通过特殊结果推断一般结论；感悟数学的严谨性，初步形成逻辑表达与交流的习惯.如何在代数教学中，尤其是运算法则教学中培养学生的代数推理能力，发展理性思维，是我们需要实践与思考的一个话题.下面以“有理数的乘法（1）”的教学为例进行说明.

一、教学内容分析

“有理数的乘法（1）”选自浙教版《义务教育教科书·数学》七年级上册第2章“有理数的运算”的第3节，是学生经历数系扩充后学习的又一种运算.前面学生学习了有理数的加减运算，经历了“从生活实例抽象—从数学角度推理—抽象归纳法则”这一学习过程，积累了一定的学习经验.但在有理数的乘法运算中，生活中很少有学生容易理解的两个负数相乘的实例，其发现、推理的过程比较复杂、抽象，需要经历从“生活—数学”“数学—数学”的二次抽象，以及“数”与“形”的多角度推理表征.因此，这对学生来说是难点，对学生的抽象能力、推理能力等提出了较高的要求.但这也是发展学生的抽象能力、推理能力等数学核心素养的良好载体.

二、制订素养导向的教学目标

《标准》指出，教学目标的确定要充分考虑核心素养在教学中的达成.每一个特定的学习内容都具有培养相关核心素养的作用，要注重建立具体内容与核心素养主要表现的关联，在制订教学目标时将核心素养的主要表现体现在教学要求中，要处理好核心素养与“四基”“四能”的关系.基于以上理念和课程内容，针对本节课，制订如下素养导向的教学目标.

（1）掌握有理数的乘法法则，发展运算能力与推理能力.

（2）经历从实际问题中抽象出数学算式，通过对数学算式的关联类比、抽象、推断出一般结论与乘法法则的过程，发展抽象能力和推理能力.

（3）从“数”与“形”多角度探索“正数×负数”“负数×负数”的代数推理，发展推理能力和几何直观.

（4）理解逻辑推理在形成数学法则和解决问题过程中的重要性，初步掌握推理的基本形式和规则，形成实事求是的科学态度与理性精神.

三、教学过程设计

1.情境引入，现实抽象

图1中显示的是位于三峡白鹤梁的用做水位测量标志的线刻石鱼.

图1 三峡白鹤梁线刻石鱼

（1）假设水位按每小时3厘米的速度上升，经过2小时后水位上升多少？

（2）假设水位按每小时3厘米的速度下降，经过2小时后水位下降多少？

师：若把水位上升记为正，水位下降记为负，由此你能得到怎样的算式？

学生根据已有经验可知：第（1）小题中，水位上升了6厘米，据此可得算式3×2=6；第（2）小题中，水位下降了6厘米，据此可得算式（-3）×2=-6.

追问：你还能列举出生活中类似的实例并用数学算式来表示吗？

学生继续从“盈利、亏损”“进货、出货”等生活实例中抽象出4×2=8，（-4）×2=-8，4×（-2）=-8和5×3=15，（-5）×3=-15，5×（-3）=-15等系列式子.

【设计意图】数学源于对现实世界的抽象.通过从生活实例中抽象出类似于3×2=6，（-3）×2=-6和3×（-2）=-6等式子，激活学生的思维，唤醒学生的已有经验，使学生自然地进行认知体系的再建构、再扩充，感受“正数×负数”和“负数×正数”的存在性与合理性.

2.探究缘由，尝试推理

师：刚才我们从生活实例中抽象出了（-3）×2=-6和3×（-2）=-6，你能从数学角度解释所列算式（-3）×2=-6，3×（-2）=-6的正确性吗？

学生类比3×2=3+3=6或3×2=2+2+2=6，推理得出（-3）× 2=（-3）+（-3）=-6，3 ×（-2）=（-2）+（-2）+（-2）=-6.

【设计意图】回归乘法的意义，类比3×2=6，推理得到（-3）×2=-6和3×（-2）=-6，注重知识的类比推理，使学生初步感受代数推理的方法，形成理性思维和理性精神.

师：刚才同学们从“数”的角度解释了（-3）×2=-6和3×（-2）=-6，你还能从“形”的角度解释一下吗？

学生类比3×2=3+3，是从原点出发向右移3个单位长度后，再移3个单位长度，那么（-3）×2就是从原点出发向左移3个单位长度后，再移3个单位长度，所以（-3）×2=-6，用数轴表示如图2所示.同理，3×（-2）=-6就是从原点出发向左移3次2个单位长度，用数轴表示如图3所示.

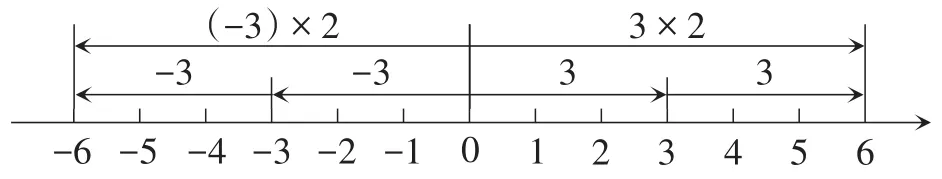
图2 用数轴表示（-3）×2

图3 用数轴表示3×（-2）

【设计意图】从3×2=6出发，从“形”的角度继续类比推理（-3）×2=-6和3×（-2）=-6，从“数”到“形”，在发展学生推理能力的同时，使学生进一步感受“正数×负数”和“负数×正数”运算的合理性.

3.关联类比，抽象结论

师：观察前面抽象得到的三组算式，每组算式的后两个算式与第一个算式的不同，你有什么发现？

（1）3× 2=6，（-3）× 2=-6，3×（-2）=-6；

（2）4× 2=8，（-4）× 2=-8，4×（-2）=-8；

（3）5×3=15，（-5）×3=-15，5×（-3）=-15.

教师引导学生从因数和积的符号变化观察思考，得出结论：两个数相乘，当改变其中一个数的符号时，其积就变为原来的相反数.

【设计意图】通过对“正数×负数”“负数×正数”的符号运算、形式推理，然后与“正数×正数”进行关联类比，从而抽象、推理出数学的一般结论和方法.在数学结论的抽象过程中发展学生的推理能力.

4.运用结论，再次推理

师：根据你发现的结论计算下列式子，并说明理由.

（1）（-4）×（-2）= ______；

（2）（-5）×（-3）= ______.

学生运用刚发现的结论“两个数相乘，当改变其中一个数的符号时，其积就变为原来的相反数”，从（-4）×2=-8或4×（-2）=-8出发，推理说明（-4）×（-2）=8.同理，从（-5）×3=-15或5×（-3）=-15出发，推理说明（-5）×（-3）=15.

追问：你还能用其他的方法来计算（-4）×（-2）与（-5）×（-3）吗？

因为（-4）× 0=（-4）×（-2+2）=（-4）×（-2）+（-4）× 2，所以0=（-4）×（-2）+（-8）.所以（-4）×（-2）=8.同理，可推导出（-5）×（-3）的运算结果.

【设计意图】基于“正数×负数”或“负数×正数”的运算结果，引导学生运用“两个数相乘，当改变其中一个数的符号时，其积就变为原来的相反数”和“数系扩充，保持原有的运算律”，从多角度推理“负数×负数”的运算结果，大力发展学生的推理能力，同时，使学生感受运算的合理性与一致性.

师：你还能从“形”的角度解释一下（-4）×（-2）=8和（-5）×（-3）=15吗？

通过“正数×负数”和“负数×正数”的数轴表示，学生发现乘上一个负号（改变其中一个数的符号），意味着将该数在数轴上所在的点绕原点逆时针旋转了180°（数轴上的反向运动），那么（-4）×（-2）就是把（-4）×2绕原点逆时针旋转180°，用数轴表示如图4所示.同理，（-5）×（-3）就是把（-5）×3绕原点逆时针旋转180°，用数轴表示如图5所示.

图4 用数轴表示（-4）×（-2）

图5 用数轴表示（-5）×（-3）

【设计意图】进一步类比“负数×正数”，从“形”的角度推理“负数×负数”的运算结果.这样，也与数系的再次扩充及“形”的再表征紧密联系起来了.之后随着虚数单位i的加入，使原有的实数系更新至复数系，乘以虚数单位i，意味着旋转90°，很好地体现了运算的一致性和思维方法的连贯性.

5.法则抽象，尝试运用

练习1：根据前面的推理，试写出下列各算式的结果.

（1）3×7= ______；

（2）（-3）× 7= ______；

（3）3×（-7）= ______；

（4）（-3）×（-7）= _____；

（5）（-4）× 5= ______；

（6）（-4）×（-5）= _____；

（7）0×7= ______；

（8）0×（-7）= ______.

师：观察上述算式，你认为两个数相乘，积的符号与这两个数的符号有什么关系？积的绝对值呢？

【设计意图】通过计算“正数×正数”“正数×负数”“负数×正数”“负数×负数”“0×正数”“0×负数”等，整体建构有理数的乘法运算，从而自然归纳、抽象出乘法法则.

练习2：用“＞”“＜”或“=”填空.

（1）（-3）+（-4）______0；

（2）（-3）×（-4）______0；

（3） 3×4 _____0；

（4）（-3）+（+4）______0；

（5）（-3）×（+4）______0；

（6）（-3）× 0 ____0.

练习3：计算下列各式.

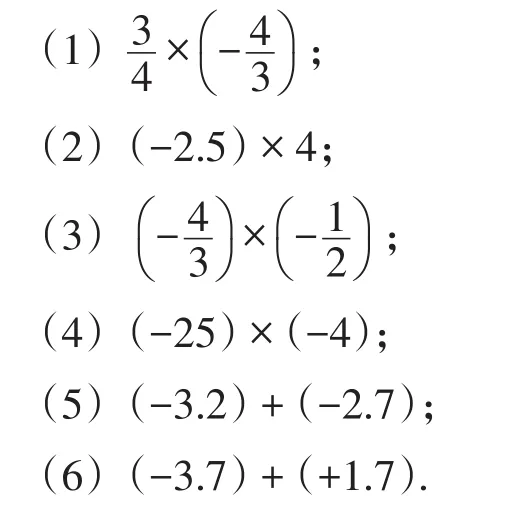
【设计意图】通过有理数的乘法和加法运算的关联类比、运用辨析，使学生感受有理数的乘法法则与加法法则的相同点与不同点，进一步熟悉、内化法则.同时，在运算过程中要求体现法则、说明算理，在发展学生运算能力的同时进一步培养其理性思维.

四、对加强代数推理路径的思考

在传统的认识中，人们往往忽视“数与代数”对培养学生推理能力的作用和价值，常常把培养推理能力的任务交给几何.事实上，几何证明中的演绎推理，并不是数学推理的全部，代数中也需要推理.在初中数学运算法则的教学中，教师要充分认识“数与代数”对培养学生推理能力的作用与价值，寻找和发现培养学生推理能力的途径.在运算法则的发现、探究过程与运用过程中融入推理能力的培养，发展学生的数学核心素养.

1.蕴“理”于数学抽象，感悟推理之意

数学源于对现实世界的抽象.通过对数量和数量关系、图形与图形关系的抽象，得到数学的研究对象及其关系；基于抽象结构，通过对研究对象的符号运算、形式推理、模型建构等，形成数学的结论和方法.数学抽象是数学的基本思想，是形成理性思维的重要基础，反映了数学的本质特征，贯穿于数学知识的产生、发展、应用的过程中.有理数乘法法则的探究过程，就是一个不断从现实问题到数学问题，再从数学问题到数学结论的抽象过程.例如，“情境引入，现实抽象”环节从现实问题中抽象出数学算式；“关联类比，抽象结论”环节与练习1中，通过对数学算式的符号运算、关联类比、抽象出数学的一般结论和乘法法则，在这个过程中，学生不断地通过特殊结果推断一般结论，感受推理之意.

2.强“理”于法则推理，习得推理之术

在乘法法则的探究过程中加强代数推理，从回归乘法本原，对“正数×负数”进行推理，然后运用“两个数相乘，当改变其中一个数的符号时，其积就变为原来的相反数”对“负数×负数”进行推理，使学生感悟数学的严谨性，逐步养成重论据、合乎逻辑的思维习惯，形成实事求是的科学态度与理性精神.数学史表明，几何表征比代数表征早了1 800年，因此乘法法则的推理不只是体现在抽象的“数”方面，还可以呈现在直观的“形”上面.例如，“探究缘由，尝试推理”和“运用结论，再次推理”环节，体现了“数”与“形”的完美结合与相互转换，升华了学生对代数推理的认识，发展了几何直观，促进了学生对乘法法则的理解和代数推理能力的进一步发展，习得推理之术.

3.重“理”于法则运用，夯实推理之基

运算能力主要是指根据法则和运算律进行正确运算的能力.运算本身是严格的演绎推理，能够促进学生推理能力的发展，有助于形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学态度.运算的每一步都是根据运算律或运算法则进行的，在法则运用过程中不仅要求学生会算，而且要明确每一步的依据是什么，即要知道算理，理解算法与算理之间的关系.例如，通过练习2和练习3，在运用法则过程中强化算理，同时通过关联、类比、辨析、拓展等，注重引导学生对法则的深度理解和整体建构，在发展学生运算能力的同时促进推理能力的发展.