意蕴悠长 自然流畅
——对“一元二次方程的根与系数的关系”一课的品赏与评析
2022-09-02郑瑄
郑 瑄
(浙江省宁波市江北区教育局教研室)
张晓鹏老师(以下统称“执教教师”)在“第十二届初中青年数学教师课例展示活动”(以下简称“展示活动”)中,为全国同仁们呈现了“一元二次方程的根与系数的关系”一课的教学及陈述分享,令笔者印象深刻,并且由此生发了有关教育教学的诸多思考.本文表达的正是笔者对这一教学展示课的欣赏与品析、感悟与感动,期盼得到思想的碰撞与谬误的指正.
一、教学理解
1.教材解读
“一元二次方程的根与系数的关系”是人教版《义务教育教科书·数学》(以下统称“人教版教材”)九年级上册第21章第2.4节的内容.该内容作为选学内容,不作为考试要求.各个版本初中数学教材对此内容的呈现方式略有不同,如表1所示.
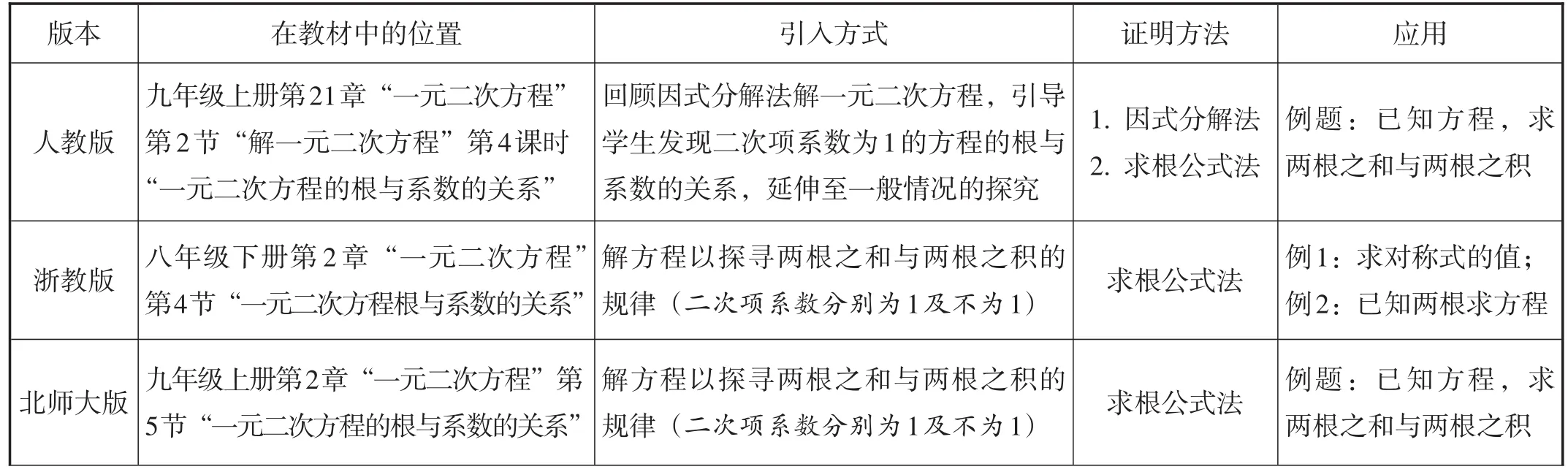
表1 各版本教材中一元二次方程的根与系数的关系编排对比分析表

续表
对于“一元二次方程的根与系数的关系”一课,以上版本教材中的相同之处为:大多安排在“一元二次方程”一章的章末;证明方法基本上采用求根公式法.
不同之处为:导入的方式各有千秋;例题及习题的编排位置等大同小异.
特别关注:人教版《〈义务教育教科书·数学〉教师教学用书》教材教师教学用书中有如下建议,虽然“21.2.4一元二次方程的根与系数的关系”是选学内容,但从一元二次方程理论的完整性、初高中知识衔接等角度考虑,本节内容都是需要学生学习的.因此,教师应当认真地完成本节内容的教学.
2.课程标准分析
早年,一元二次方程的根与系数的关系作为必学内容在教材中呈现.后来,《义务教育数学课程标准(2011年版)》将这部分内容作为选学内容,打上“*”,不作为考试要求.
现在,《义务教育数学课程标准(2022年版)》(以下简称《标准》)在这块内容的处理上有所回归,调整为必学内容.《标准》对此内容的要求为:了解一元二次方程的根与系数的关系.学生要能利用一元二次方程的根与系数的关系解决一些简单的问题,要关注基于代数的逻辑推理,如根与系数的关系的论证.
特别指出,本节课——一元二次方程的根与系数的关系,也正是本次展示活动8个指定课题之一.展示活动对这一指定课题的要求如下.
内容与要求:知道一元二次方程的根与系数的关系,能通过系数表述方程的根,能用方程的根表示系数.
教学提示:了解一元二次方程一般表达式ax2+bx+c=0(a≠0)的关键是用字母表示方程的系数,可以写出方程根的一般表达式;知道这样的表达是算术转变为代数的关键步骤.要在一般观念的引领下引导学生发现和提出研究方程的根与系数关系的问题,要引导学生通过用数学符号进行一般性推理得出根与系数的关系(韦达定理)的猜想,并能通过代数推理论证给出证明,在此过程中感悟符号表达对于数学发展的作用,积累用数学符号进行一般性推理的经验.
3.教学思考
客观地说,对教学实施而言,由于之前一元二次方程的根与系数的关系是选学内容,不作为考试要求,因此教师在教学中处理这块知识内容时存在着如下一些现象:有些教师将其作为阅读材料,有些教师让学生自学,有些教师甚至直接放弃教学,但也有些教师严格按照教材呈现的知识有序地进行教学,还补充一些利用一元二次方程根与系数关系的知识解决一些经典习题,等等.
对一元二次方程的根与系数的关系,教师可以思考以下问题:
(1)教,还是不教?
(2)教,教到何种程度?
(3)教学目标如何定位?重点、难点究竟何在?
进而引发如下更深层次的思考:
(4)何以想到要去发现和探究一元二次方程的根与系数的关系?(来自逆向思维的启示:譬如乘法公式与因式分解、几何图形的性质与判定等,抑或其他?)
(5)为何确定两根之和与两根之积为研究对象?
(而非两根之差与两根之商?)
(6)研究方法、证明思路从何而来?每一种证明其合理性何在?(来自数学历史文化进程相似性的类比.)
(7)方程的根与系数之间的联系还有其他表现形式吗?(来自培养研究意识、研究方法、研究能力的目标启思.)
事实上,在平常的教学中,尽管这是一节选学内容,但还是有许多教师对这节课感兴趣,对教学方法进行深入地思考、实践和研究,并且为其撰文、发表观点.为什么?以笔者的理解,这是一节以数学探究为载体,几乎经历了探究全过程(感觉—提问—观察—猜想—发现—归纳—验证—推理—结论)的一节课,还有什么比探索新知、发现新奇、收获新得更令人痴迷而向往的呢?执教教师正是对于本节课秉持十分审慎而认真的态度,以专业的学术精神来对本节课的内容进行诠释.
二、亮点赏析
可以用明快的词语概括本节课:意蕴悠长,自然流畅.
意蕴悠长:悠,表达着时间;而长,表达着空间.本节课中蕴含着悠长的数学历史文化,又彰显着数学探究过程充满理性、严谨的数学思维.
自然流畅:理解数学——顺应数学学科教育教学的发生、发展规律;理解学生——顺应学生学习认知的生长、成长、发展规律,在这双重信念的追求之下架起理解教学的桥梁,让数学教育教学自然生发,静水深流.
通常来说,对于“一元二次方程的根与系数的关系”的教学,最便捷的教学方法是快速找到一元二次方程两根之和、两根之积与系数的关系,然后以较多的时间来进行形成性、巩固性、拓展性的练习和强化训练.而“引导学生发现和提出研究方程根与系数关系的问题”(即来自指定课题的教学建议),这一知识的发生、发展过程恰恰会被忽视和轻视.忽视,即无意识;轻视,导致重点转移.
在此环节,从诸多公开课及文章文献中可以看出广大同仁的行动和作为.例如,给定一些一元二次方程,计算两根之和与两根之积以发现规律;为了追求数学的简洁美,计算两根的和、差、积、商,以发现规律;已知一元二次方程,计算关于其两根的对称代数式;利用求根公式直接计算两根之和与两根之积;因式分解观察法;设而不求法;等等.
所有的种种努力都希冀探索、发现一元二次方程的根与系数的关系,方法各有千秋,背后都有其数学思考和历史渊源.例如,韦达、拉克洛瓦的设而不求;欧拉的因式分解,19世纪以来教材中的求根公式法.
本节课中,执教教师的教学思考与设计非常令笔者欣赏.具体体现在如下几个方面.
1.引人入胜的问题提出
问题情境:已知矩形的长和宽分别是一元二次方程x2-1 234x+5 678=0的两个实数根,求这个矩形的周长和面积.
教学中,学生认为用学过的方法解这个方程会很麻烦,于是思考是否还有其他方法,不解方程是否能快速求出矩形的周长和面积,即求方程的两根之和与两根之积.
尽管这个方程本身有些许不自然的人为痕迹,但是它引发了学生的思考,不动声色地指向了今天的课题,即两根之和、两根之积与一元二次方程系数的关系.这样的行为避免了教师的主观和指令,而且它还有良好的数学历史文化意蕴.
古巴比伦泥板书上出现了历史上第一批一元二次方程,其中一个问题为:一块矩形田地面积为55,长边比短边多6,问长边多长?后续,有教师将其改编为“已知矩形的周长与面积,求长和宽”的问题;而今,执教教师在教学中又赋予其新的生命力和生长力.如何自然而科学地发现问题、提出问题,是培养学生拥有探究意识、找准研究方向的重中之重.
2.耐人寻味的过程探究
正因为问题提出得自然合理,所以使得探究活动1及探究活动2的填表、观察、猜想各司其职,使表格目标明确,使观察一目了然,使猜想接近真相.
探究的过程,是逐步走近真理的过程,更是数学思维进阶的过程.本节课中,如下几个细节较为出色.
其一,执教教师的整个探究过程的设计逻辑清晰、框架合理、设计精妙、脉络自然,给予学生以数学研究途径与方法的指引,并且使得数学探究的思维可视化,还为学生在今后其他知识内容的探究甚至其他领域的探究提供了可供迁移的素材.
其二,执教教师在引导学生经历、领略各种证明方法(因式分解法、求根公式法)的探究过程中,不仅开阔了学生的视野,潜移默化地培养学生通过用数学符号进行一般性推理的能力,还培养了学生的代数推理能力.对于数学思想方法的归纳,也同样自然而为——从二次项系数为1到不为1所彰显的从特殊到一般思想,以及系数不为1时各种推导方法之间的转化思想,均在教学中自然而然地生成.
其三,也是令笔者最为感动的——师生互动.教师的询问与学生的呼应很精彩.我们依稀看见执教教师正带领学生一步一步地走向科学之路.同时,执教教师十分注重细节的处理.
例如,如下对话.
师:对于分子,你是怎么处理的?
生:可以运用平方差公式.
师:能直接除吗?
生:能直接除,因为a≠0.
蓦然联想到苏轼在《文说》中有言:吾文如万斛泉源,不择地而出,在平地滔滔汩汩,虽一日千里无难.及其与山石曲折、随物赋形而不可知也.其中,随物赋形,是否可以这样理解——水遇到平地,是缓缓而流;遇到阻隔,则婉转环绕;遇到陡峭之处,疾泻而下;遇到沙土腐叶,浸润其中.所谓“以生为本”是也.
三、教育省思
本节课中有一个细节发人深省.教学片断如下.
师:请编写一个方程,来验证刚才的猜想对不对?
生1:2x2+3x+9=0.
师:找一个更简单的二次项系数为1的方程.
生1:x2+2x+3=0.
……
其实这个细节值得关注.学生列举的两个方程,其实它们的根的判别式都小于0,这很有价值.在本节课中,有三次涉及判别式Δ:一次是在开课伊始回顾求根公式时;一次是在典例示范时直接给出;还有一次是在最后小结时用一句话提点,但稍有飘忽.教师在此处是否可以有所设疑?有所留白?因为当Δ<0时,两根之和与两根之积确实可以由计算得到,但仔细考量,在初中阶段,两根之和与两根之积并无意义.而在更大的数域范围内,一元二次方程根与系数的关系仍然成立.况且本节课所说的根与系数的关系仅仅只是韦达定理的一种特殊情况,它有更为广阔的天地.
圣·埃克苏佩里撰写的《小王子》一书中有这样一段话:如果你要造船,不要招揽人来搬木柴,不要给人指派任务和工作,而是要教他们去渴望那广袤的大海.
而设疑和留白,也许会激发更为深远的好奇之心、探究之意和品赏之乐!
四、结束语
本节课中,执教教师立于本源之地,在一般观念的引领下,引导学生发现和提出研究方程的根与系数关系的问题,并通过观察、猜想、验证、推理、归纳以经历探究的全过程,最终使学生获得的不仅仅是知识,更多的是数学研究意识、研究方法和研究能力.而由此引发的数学探究的态度和精神,必将超越知识的存在而根植于学生的心中,此乃数学独特的育人价值和希望所在.这样的课例展示具有启发与示范作用.而本文品赏与评析的要义也正基于此.
为期两天半的展示活动是全国初中数学教育教学研讨的盛会.于笔者而言,观摩与学习的同时,更增添了检审与省思,进一步引发了我们数学教师的哲学思考:数学教育教学究竟要带给学生什么?
为人师者,立德树人;数学教育,任重而道远.
