基于试验对标法的轿车行李箱扭杆耐久性研究

程雪利，陆志成，安林超

（1.河南工学院 机械工程系，河南 新乡 453000；2.神龙汽车有限公司 技术中心，湖北 武汉 430056）

0 序 言

扭杆铰链组件是轿车行李箱盖的关键部件之一，利用扭杆变形产生扭矩实现行李箱盖的启闭。扭杆结构简单，成本低，目前大多数家用轿车采用弯管式铰链配扭杆启闭行李箱。在轿车行李箱耐久性试验中，会出现扭杆断裂失效，影响行李箱耐久目标性能和人机操作性能。国内外学者围绕轿车行李箱扭杆开展了各种研究：李世泽等［1］建立扭杆行李箱系统动力学分析模型，对四连杆尺寸及扭杆参数进行DOE优化，提高了扭杆疲劳耐久性能；张智千［2］应用力学原理和数学方法对扭杆弹簧受力原理进行分析，建立了用户手部作用力与行李箱盖开启角度之间的数学关系；张晓东等［3］将某款SUV车型直线扭杆结构优化为弯曲扭杆结构，并利用仿真分析软件证明了优化结构的合理性；董炳健等［4］提出了自由杆式扭杆弹簧平衡机构的设计校核方法，给出一种改良行李箱盖平衡区域的方法；邢艺文等［5］提出了一种空心杆结构形式扭杆；张克俭［6］提出了一种提高大直径扭杆弹簧淬火态硬度的新方法，采用该方法可以大大提高扭杆的疲劳寿命；徐璐［7］重点对扭杆弹簧典型结构、制造工艺及材料、装配工艺及设计应用进行了论述；李超帅等［8］采用Excel对行李箱全开闭角度的开闭力进行了计算，提出行李箱盖开闭力与平衡角度的一种设计优化方法；胡宏等［9］采用VB对行李箱盖扭杆四连杆铰链布置的计算方法程序化，寻找出最优的连杆铰链布置方案；曾毅［10］分析了轿车的行李箱盖平衡铰链的力学原理并给出扭杆设计过程；刘福强等［11］通过调整扭杆的角度对整个行李箱盖开闭状态进行了优化；杨潆奎等［12］提出了一种对汽车开闭件进行关闭冲击仿真的建模方法，基于该模型对汽车行李箱盖的耐久性进行了仿真分析和试验验证。以上研究为提高行李箱扭杆性能做出了贡献，但大多是对扭杆进行结构优化、参数设计以及进行静力学和动力学仿真分析，直接针对扭杆采用试验对标法开展耐久性试验的研究比较少。

本文针对扭杆在耐久试验中出现的断裂失效问题，首先确定对标参数，然后对影响扭杆的外载荷、CAE仿真结果的网格类型、网格尺寸大小、扭杆驱动方式及连接方式等参数进行试验对标；基于对标参数结果对扭杆结构进行优化，通过优化迭代分析找到扭杆的最优结构方案，最后通过仿真结果和试验结果对标验证优化结构的合理性。

1 扭杆试验对标参数确定

间接式行李箱扭杆结构如图1所示，主要由扭杆、鹅颈管、扭杆支架和固定支架组成。扭杆一端固结在固定支架上，另一端与扭杆支架连接，扭杆支架和鹅颈管铰接在一起。通过对扭杆弹簧的参数优化及合理布置，可以提高行李箱盖的开闭性能［13］。在行李箱扭杆耐久性研究过程中，扭杆承受的外扭矩、扭杆网格单元类型和尺寸大小、扭杆驱动方式和扭杆连接方式对耐久性结果影响较大，因此选取这些参数作为对标参数，将其CAE数据与试验结果对标［14］。

图1 间接式行李箱扭杆结构Fig.1 Structure of indirect trunk torsion bar

2 扭杆仿真模型建立与对标试验

2.1 扭杆外载荷试验标定

图（1）中，扭杆、鹅颈管、扭杆支架和固定支架构成四连杆机构OHMN，如图2所示。其中，固定支架OH为机架，扭杆ON和鹅颈管HM构成连架杆，扭杆支架MN为连杆，扭杆ON转角变形提供动力。

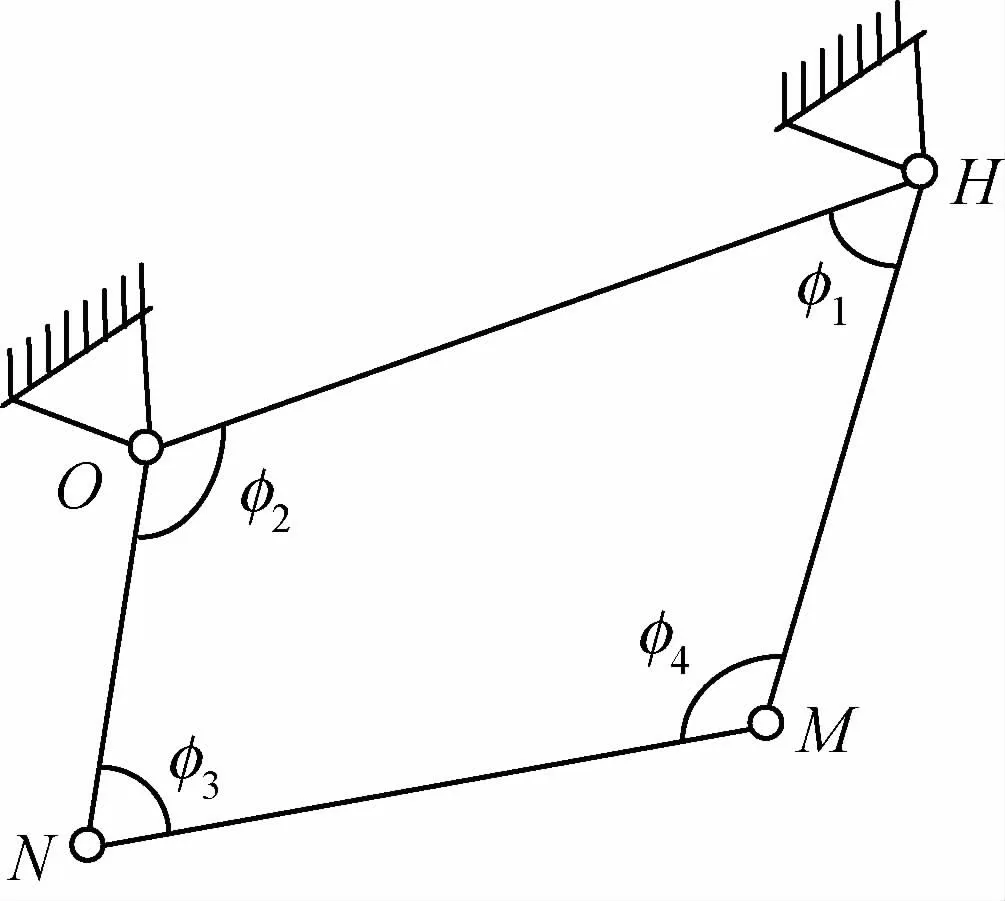
图2 间接式行李箱扭杆的四连杆机构Fig.2 Four connecting rod mechanism of indirect trunk torsion bar

2.1.1 扭杆作用力计算

扭杆扭矩由其变形角产生，单根扭杆重力矩

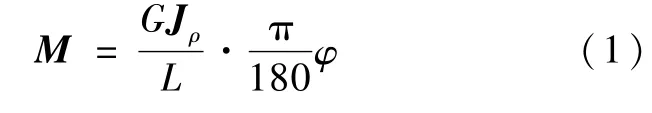
式中：G为冷轧LAC340Y410T钢材料的剪切弹性模量，8.2×104MPa；Jρ为截面的抗惯性扭矩，Jρ＝πd4／32，d为扭杆直径，6.5 mm；L为扭杆的有效长度，1 030 mm；φ为扭杆变形角。

式（1）中，材料的剪切弹性模量G、截面的抗惯性扭矩Jρ以及扭杆的有效长度L为恒定值，扭杆变形角φ随着行李箱盖的启闭发生变化。通过试验标定可知四连杆的初始角φ为140.85°，随着行李箱开启，φ逐渐减小，修正后，

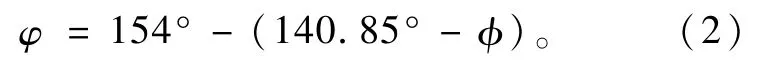
考虑到扭杆的初变形和整车在涂装车间的烘烤，扭杆有5%的失效率，继续对扭杆变形角修正，修正后为

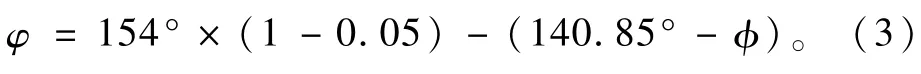
将式（3）代入式（1）中，得到单根弹簧扭矩的标定计算公式为

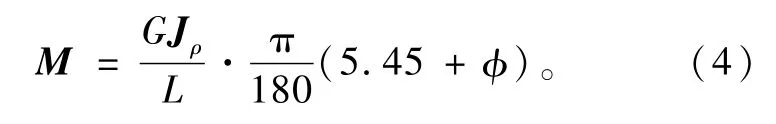
2.1.2 扭杆摩擦力矩计算

扭杆在工作过程中，除了承受扭矩M之外，和扭杆支架之间还存在摩擦力矩，为精确计算扭杆平衡力矩，需考虑摩擦力偶距的作用。扭杆产生的力矩M由平衡力矩M′HM和扭杆支架的摩擦力矩Mf平衡，力矩平衡方程为

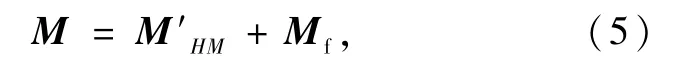
扭杆ON的力矩平衡方程为

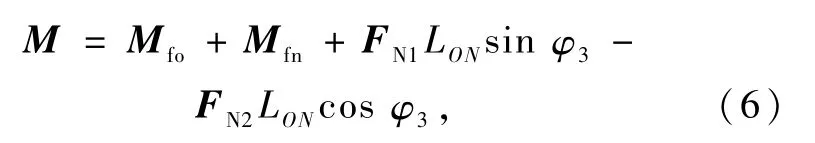
连架杆HM所受的力矩平衡方程为

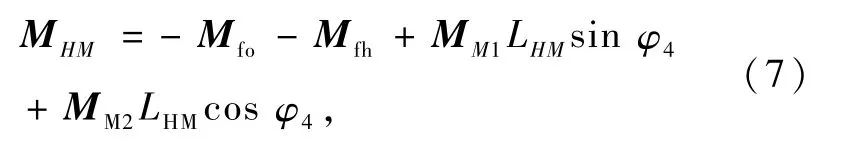
根据式（5）～（7）推导摩擦力偶矩计算式

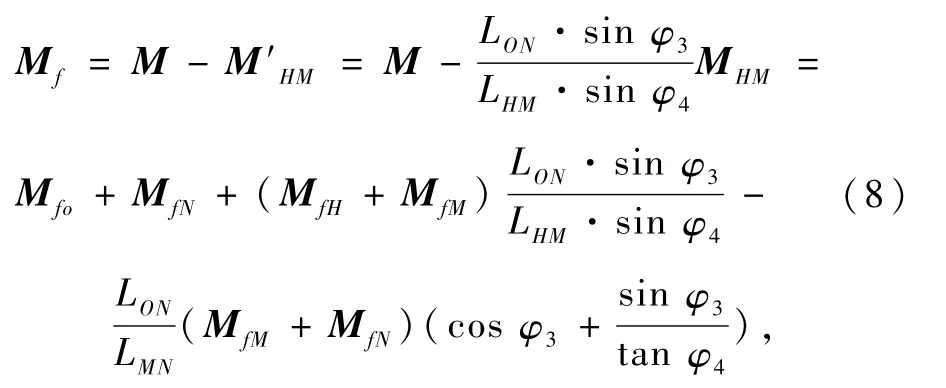
式中单点摩擦力矩根据试验标定为

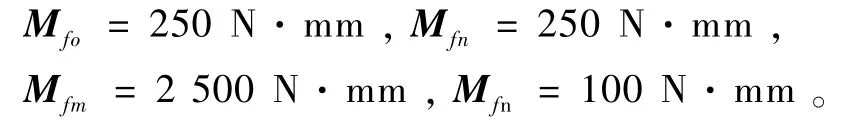
2.2 网格单元类型和尺寸大小试验标定

扭杆CAE模型采用实体四面体或六面体单元。建立扭杆CAE模型，并比较四面体和六面体单元在位移、应力和计算时间上的差异，如表1所示。由表1可知，一阶线性单元在计算时出现剪切自锁，造成单元刚度大，计算精度低；二阶缩减积分单元计算时无剪切自锁，应力计算结果精确，计算时间比完全积分时间短，适于模拟应力集中，故选用C3D20R二阶缩减积分单元［15］。

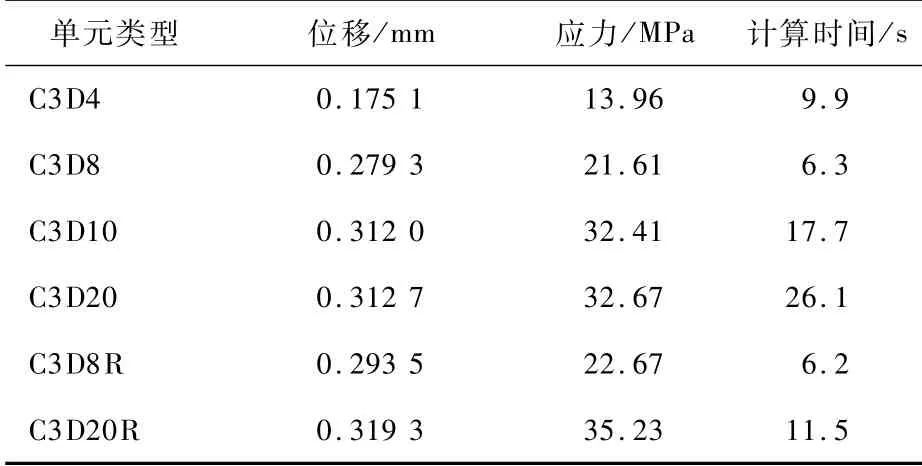
表1 网格单元类型的比较Tab.1 Comparisons of grid cell types

扭杆截面为圆形，在圆周方向单元尺寸越小、单元数目越多，与实际几何模型贴合性越好，但单元尺寸过小，会使计算时间过长。因此，在保证计算精度的前提下，确定单元尺寸为1.5 mm。

参照扭杆试验的边界条件，选择C3D20R网格单元，对扭杆安装到行李箱盖上转过的角度和行李箱从开启到关闭状态转过的角度进行CAE仿真计算和试验标定（图3），对标结果如表2所示。从表2可以看出，扭杆扭矩的仿真值和试验值在两个位置的误差均小于1%，吻合度较好。

图3 扭杆网格对标试验Fig.3 Benchmarking test of torsion bar grid

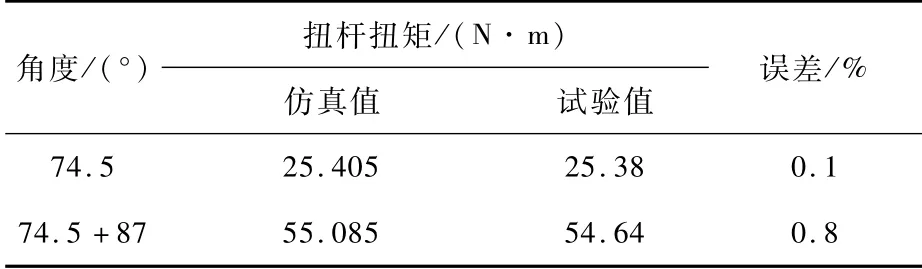
表2 扭杆网格对标数据Tab.2 Benchmarking data of torsion bar grid

2.3 扭杆驱动方式标定

CAE分析过程中，扭杆的驱动方式有角度驱动和位移驱动。将建立的扭杆模型导入ADAMS软件中，并施加约束进行运动学仿真分析，得到扭杆中心线在X／Z方向上位移与角度之间的函数关系，将其转化为位移与时间的关系曲线，如图4所示。运用ABAQUS进行求解分析，发现转角驱动不能使扭杆达到启闭的极限位置，而双位移驱动可近似达到，比转角驱动的结果更接近扭杆实际工况，如图5所示，CAE分析时为扭杆添加双位移驱动［15］。

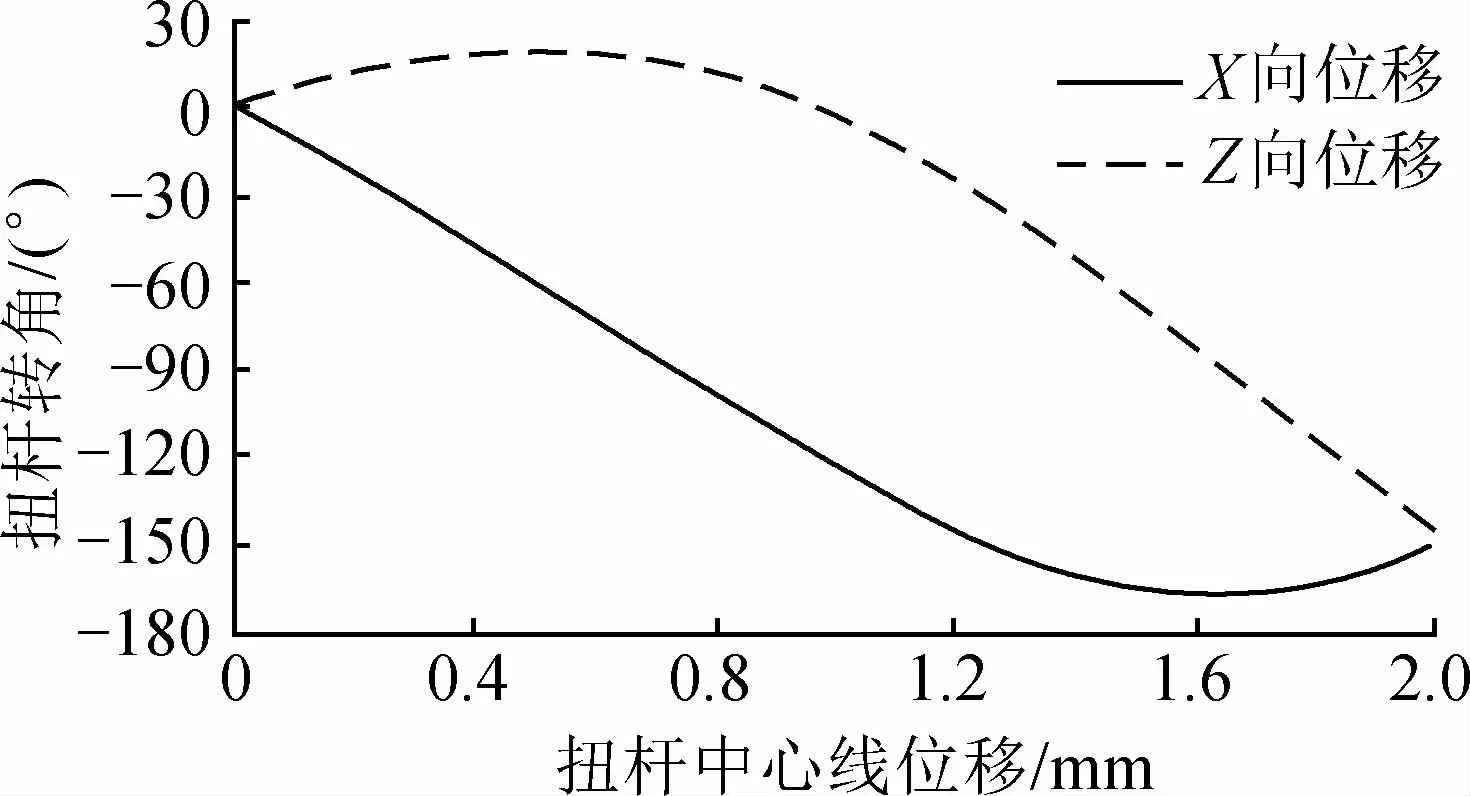
图4 X／2方向位移与角度关系Fig.4 Relationship between the direction displacement and the angle of X／Z

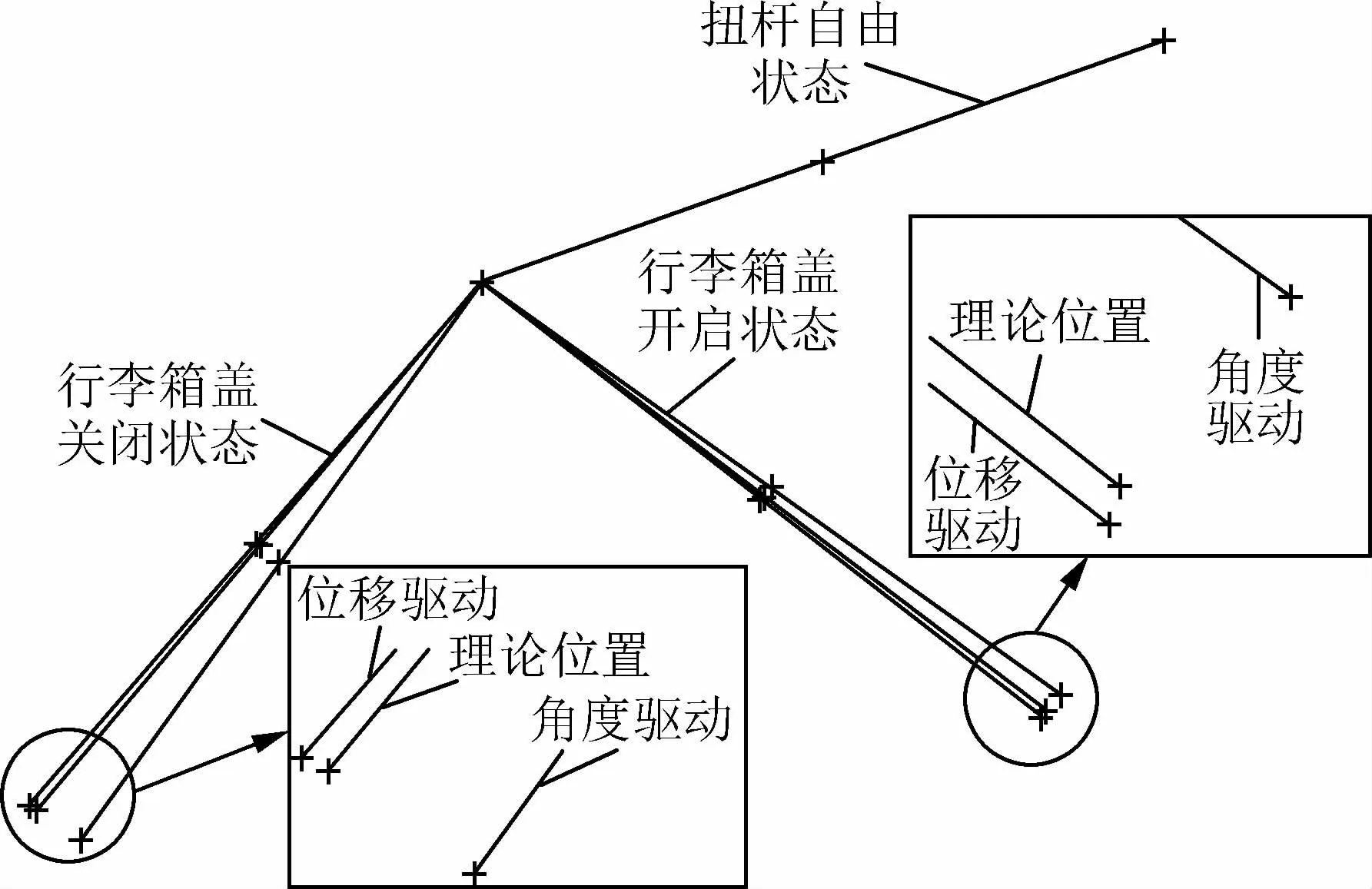
图5 扭杆驱动方式比较Fig.5 Comparisons of torsion bar driving modes

2.4 扭杆连接方式确定

在行李箱开闭过程中，扭杆与扭杆支架之间实际存在相对转动，如图6（a）所示。通过仿真结果比较发现，考虑扭杆与扭杆支架之间的相对转动，危险区域最大应力为1 509.1 MPa，如图6（b）所示；不考虑扭杆与支架之间的相对转动，危险区域最大应力为1 509 MPa，如图6（c）所示，所以该因素对分析结果几乎无影响。但如果考虑相对转动关系，系统需增加一个转动自由度，计算时间增加4倍，且易导致计算过程不稳定。因此，最终的仿真模型不再考虑扭杆与扭杆支架的相对转动。

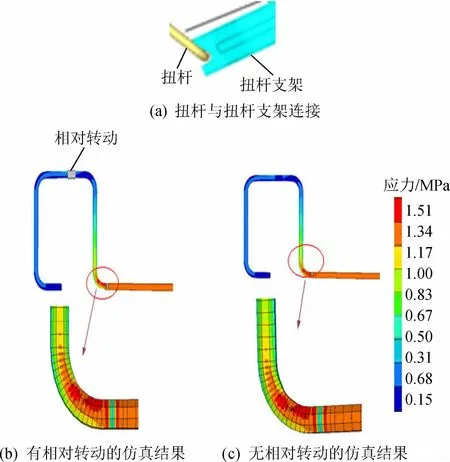
图6 扭杆的应力分析Fig.6 Stress analysis of torsion bar

根据行李箱盖开闭耐久试验的要求及上述影响因素的分析，采用缩减二次积分单元，单元大小为1.5 mm，运用双位移驱动方式对扭杆进行分析计算，得到扭杆应力结果，如图7所示。

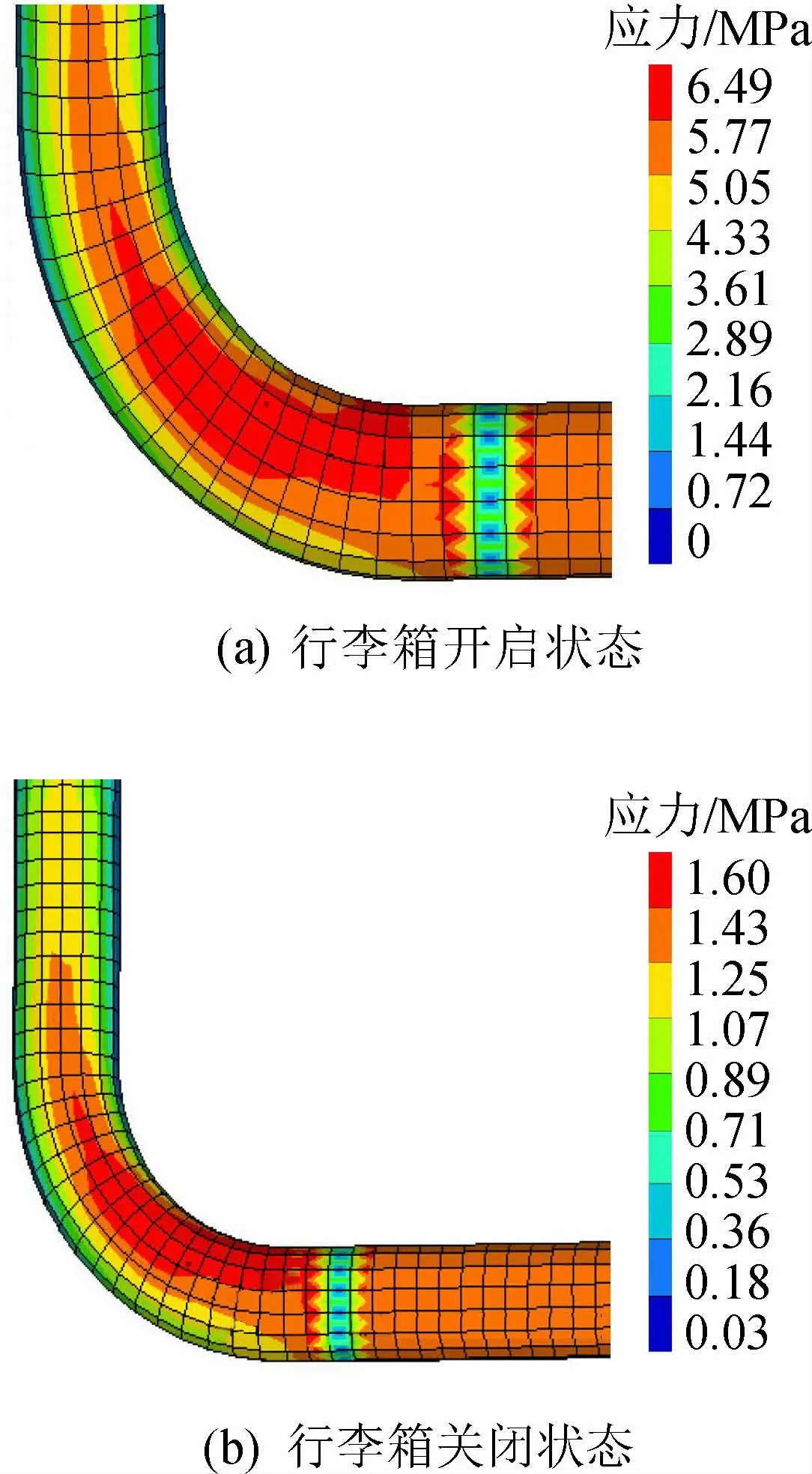
图7 扭杆应力结果Fig.7 Stress result of torsion bar

从图7可以看出，应力最大区域出现在折边过渡区，与耐久性试验断裂区域吻合。行李箱开启状态扭杆应力值为649 MPa，行李箱关闭状态扭杆应力值为1 603 MPa，开启到关闭过程中扭杆应力的变化为954 MPa。

耐久损伤寿命N的Basquin公式为

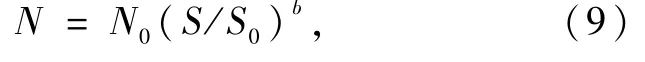
式中：N0为参考寿命50 000次；S为计算的应力值；S0为应力标准886 MPa；b为Basquin斜率。

根据式（9），计算出扭杆的寿命为27 672次，试验值为27 950次，仿真值与试验值对标较好，验证了所建模型的有效性。

3 扭杆结构优化设计及试验验证

3.1 结构优化方案

通过对扭杆CAE分析可知，扭杆工作时应力最大区域出现在折边过渡区，降低折边过渡区应力是提高扭杆耐久性能的关键。对扭杆可从以下方面进行优化：（1）改变扭杆矩形区域和杆长（方案1和方案2）；（2）优化破坏区域折弯半径，使过渡平滑（方案3）；（3）增加扭杆自由状态下的扭转角（方案4）。具体优化结构如图8所示。

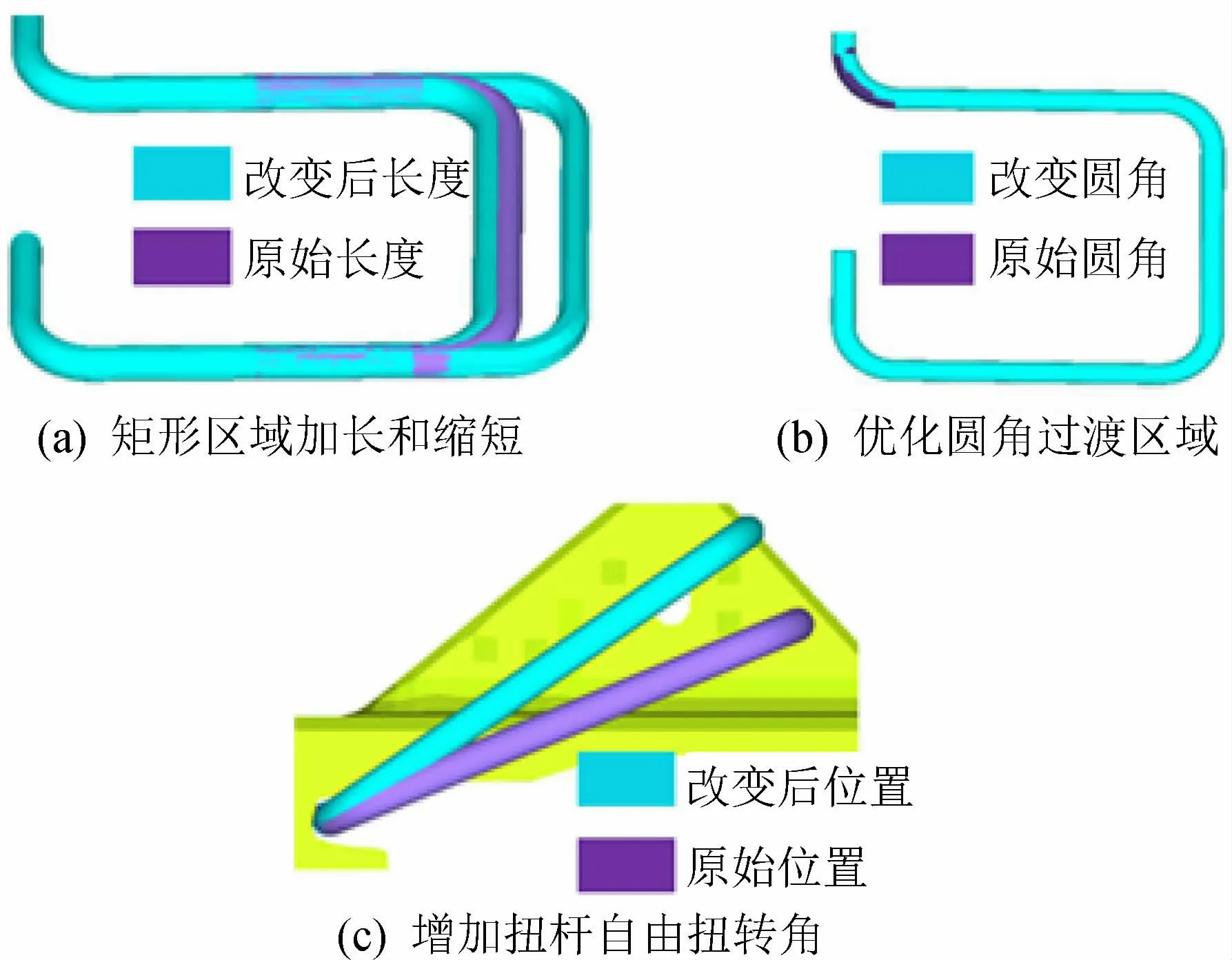
图8 扭杆结构优化方案Fig.8 Structure optimization schemes of torsion bar

以文中试验标定的参数为依据，进行不同方案的CAE计算和优化迭代分析，结果见表3。

从表3可以看出，扭杆矩形区域的尺寸变化对应力值影响不大；将断裂区域的圆角平顺后，最大应力降低33 MPa；增加扭杆的自由扭转角，使扭杆装配到整车上的预备力矩增大，最大应力降低56 MPa；结合方案3和方案4，优化圆角过渡区域的同时增加扭杆自由扭转角，使扭杆应力传递平稳，结构强化，最大应力和计算寿命满足5万次的耐久性能要求。

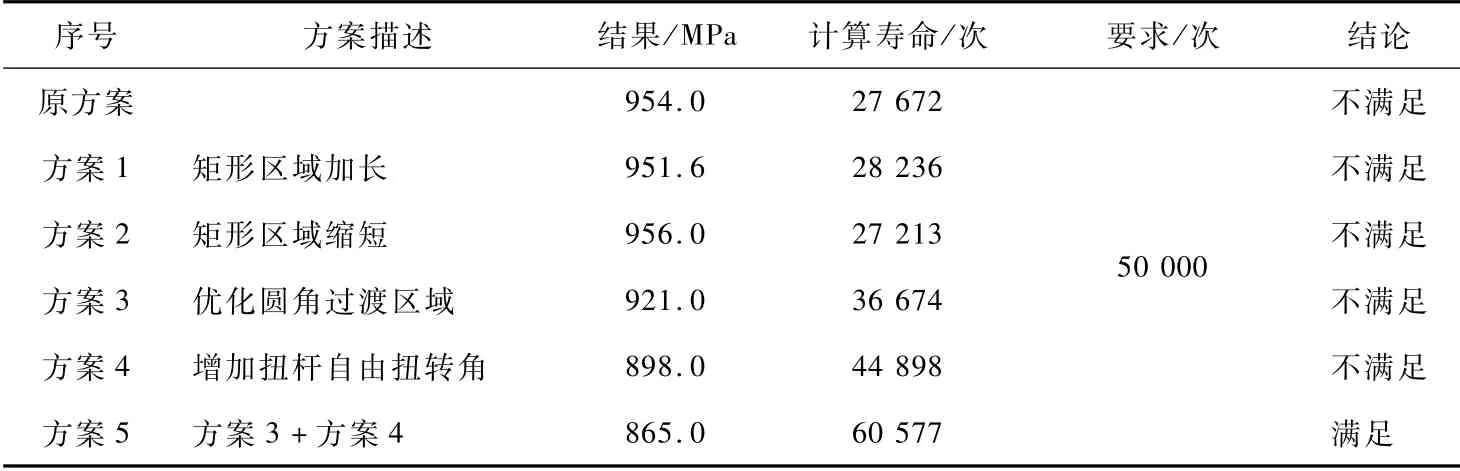
表3 扭杆结构优化结果Tab.3 Optimization results of torsion bar structure

3.2 优化方案试验验证

以上述试验标定的参数和优化结果建立仿真模型，在ADAMS软件中对扭杆启闭进行运动学仿真分析，结果如图9所示。根据优化方案制作试验样件，在行李箱盖耐久试验台架上对改进后的扭杆进行启闭耐久试验，如图10所示。

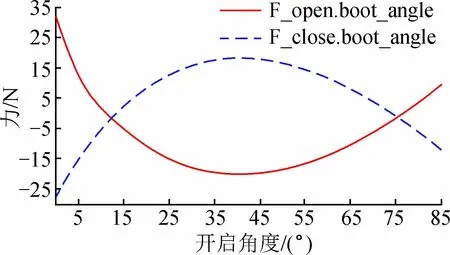
图9 开启／关闭力随行李箱盖开启角度的变化曲线Fig.9 Change curves of opening and closing force with opening angle of trunk lid

图10 优化后扭杆开闭耐久试验Fig.10 Endurance test of torsion bar opening and closing after optimization

由图9分析可知，最大开启操作力和最大关闭操作力分别为32.3 N和27.1 N，启闭第一平衡角为12.9°，第二平衡角为75°，启闭力和启闭平衡角均满足人机操作性能要求。试验结果显示，优化后行李箱盖的耐久性能大幅提高，在性能要求的50 000次范围内，扭杆无断裂，功能完好，满足行李箱盖启闭耐久性能要求。

将CAE仿真分析结果和试验结果对比标定，结果如表4所示。从表4可以看出，CAE分析结果与试验结果一致性较高，证明了该对标分析在扭杆优化过程中的有效性。

表4 行李箱开闭仿真与试验结果对标Tab.4 Simulation and test results benchmarking with the trunk opening and closing

4 结 论

（1）针对轿车行李箱扭杆断裂问题，分析识别出影响扭杆CAE仿真的网格类型、网格尺寸大小、扭杆驱动方式和连接方式等参数，通过试验标定，确立四连杆机构的外载荷，建立有效的有限元分析模型，为扭杆优化研究提供了理论基础。

（2）提出改变扭杆矩形区域长度、圆角过渡区域平顺性以及自由状态下扭转角等结构优化方案，在标定参数结果的基础上，对不同优化方案进行了CAE计算及优化迭代分析，得出优化圆角过渡区域+增加扭杆自由扭转角能满足最大应力和计算寿命要求，是最优方案。

（3）对优化方案进行CAE分析结果和试验结果对标，可得：最大开启操作力、最大关闭操作力、启闭第一平衡角和第二平衡角均满足人机操作性能的要求；在性能要求的50 000次范围内，扭杆无断裂，功能完好，满足行李箱盖开闭耐久性能要求。对标结果的一致性，证明了该对标分析在扭杆优化过程中的有效性，可为类似结构设计及优化提供参考。