瓦斯爆炸冲击波作用下防爆门应力分布及动态响应特性研究
2022-09-02马尚祯温小萍
马尚祯,温小萍
(1.河南能源化工集团鹤煤公司 陕西富源煤业有限公司,陕西 延安 727502;2.河南理工大学 机械与动力工程学院,河南 焦作 454000)
0 引 言
煤矿风井防爆门是一种可防止瓦斯、煤尘爆炸时毁坏主要通风机的安全设备,且在主要通风机停运时可以打开,起到防止井下硐室和主要回风巷道瓦斯积聚的作用[1-4]。当瓦斯爆炸发生时,防爆门在强大爆炸冲击压力波作用下,容易发生变形甚至损坏而无法关闭,致使反风时风流短路,井下有毒气体排出困难,影响井下救援工作[5]。针对该问题,国内外已有学者对防爆门的密封结构、冬季易结冰、备用防爆门快速复位及锁扣等问题进行了相关研究[6-8],但考虑实际爆炸冲击波作用下的防爆门动态响应过程进行分析仍然较少,与此同时,通过数值模拟分析防爆门强度及结构优化也不常见[9-12]。因此,针对某煤矿风井进行防爆门结构设计的基础上,利用FLUENT软件对瓦斯爆炸冲击波压力作用下防爆门动态响应过程进行数值模拟,得出瓦斯爆炸冲击波在不同时刻作用于防爆门上的压力分布及其运动规律,同时运用ANSYS软件对防爆门进行动态受力分析,在此基础上,对防爆门现有结构进行了优化和强度校核。
1 防爆门结构设计
目前,煤矿风井防爆门结构形式主要有伞式、花瓣式、蝴蝶式等[13]。在矿井灾变时期,瓦斯爆炸或瓦斯与煤尘复合爆炸当量不可估计,因此防爆门抗冲击强度无法准确确定,容易导致在受到爆炸冲击作用时压力在防爆门中心底部积聚,致使防爆门变形破坏。本文设计的风井防爆门为双开式结构,两扇门可以绕各自转动轴自由转动,转动角度为0~90°,其作用是在风井需要密封时,双开式防爆门将井口封盖,当瓦斯发生二次爆炸或多次爆炸时,防爆门能自动开启,并在爆炸过后自动复位。
双开式防爆门结构如图1所示。风井直径为4.8 m,方形密封池为7.5 m×7.5 m×4.1 m;单扇防爆门为2.735 m×5.2 m,厚度3 mm,门框为50角钢,单扇防爆门质量为480 kg,配重质量为775 kg。为了简化井筒示意图,配重在图1中未画出,但在防爆门运动计算过程中加以考虑。
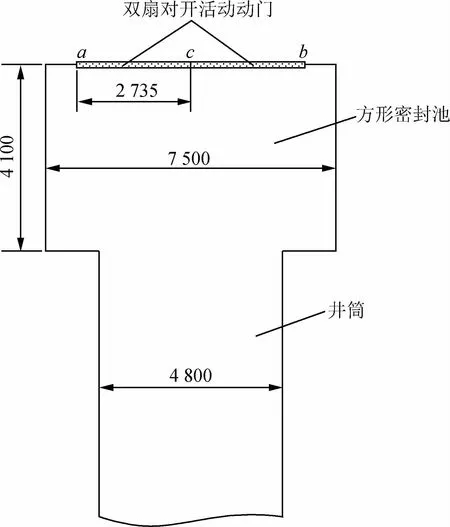
图1 防爆门总体结构设计Fig.1 Overall structure design of explosion-proof door
2 防爆门动态响应特性
为了分析防爆门在瓦斯爆炸冲击波作用下的安全可靠性,采用FLUENT软件对瓦斯爆炸压力场进行数值模拟,得出防爆门上的压力分布及防爆门运动情况。
防爆门物理模型是根据实际防爆门尺寸按照1∶1建立,为提高计算精度,靠近壁面处的计算网格进行局部加密[14-15],如图2所示。图2中ac和bc为双开式防爆门,分别设为可绕a点和b点转动的刚体,其余均为固定壁面。防爆门转动角加速度根据牛顿第二定律确定,即与所受压力和重力(包括活动门和配重)的力矩代数和成正比。井筒和方形密封池充满化学当量比的CH4和空气预混气体。初始时刻,在井筒底部利用局部高温(2 400℃)方法点火引爆。流动为非稳态湍流流动,湍流模型采用k-ε湍流方程,壁面采用标准壁面函数,燃烧反应采用适用于湍流燃烧的EBU涡扩散模型,并采用收敛较好的PISO算法进行迭代求解,时间步长设为1×10-5s。模拟获得混合气体最大爆炸压力为782 kPa,爆炸冲击波传播计算时间为100 ms。

图2 煤矿风井防爆门物理模型及计算网格Fig.2 Physical model and computational grid of explosion-proof door of coal mine air shaft
爆炸冲击波到达活动门的初始压力较小,由于气流受阻而使压力升高。在点火后24 ms时刻,活动门压力分布最高仅为26 kPa。图3(a),(b),(c),(d)分别为爆炸冲击波作用下防爆门开启至5°,25°,45°,90°时的压力场。可以看出,防爆门开启初期,由于防爆门开启角度小,泄爆口较小,使气流积聚,压力持续升高,防爆门所受的最高压力由26 kPa上升至782 k Pa,活动门上平均压力由23 k Pa上升至467 k Pa。当防爆门开启角度增大时,所积聚压力得到足够释放,压力开始逐渐下降。

图3 不同角度时防爆门的压力场Fig.3 Dynamic opening process of explosion-proof door at different angles
图4(a),(b),(c),(d)显示了防爆门角度分别为5°,25°,45°,90°时防爆门下方的压力分布。当开启角度为25°时,防爆门上压力分布不均匀,靠近转动轴位置的压力最高,泄爆口附近压力最低,说明防爆门泄爆作用十分显著,但由于泄爆口较小,使防爆门上的最高压力仍然较高。当开启角度为90°时,防爆门上的压力较为均匀,已下降至220 k Pa左右。可以看出,由于冲击波的初始压力较小,防爆门在刚开启时角加速度较小,开启速度较慢,之后角加速度随之增大,开启速度增加较快。因此在满足材料强度前提下,应尽可能减小活动门及配重的质量,从而提高防爆门开启速度,这样可以防止压力过高。
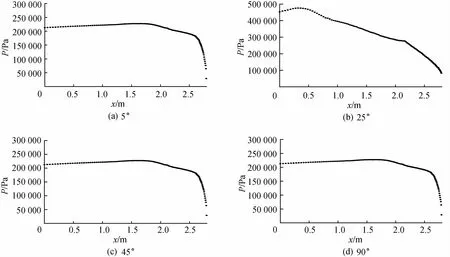
图4 不同角度时防爆门下方的压力分布Fig.4 Pressure distributions under explosion-roof door with different angles
3 防爆门强度分析
采用ANSYS(9.0版本)结构分析软件,对单扇活动门在动态非线性压力作用下的应力及变形进行分析计算,并通过校核材料强度,判断变形类型属于弹性变形还是塑性变形,从而检验活动门的安全可靠性。
单扇防爆门尺寸为2.735 m×5.2 m,门框为50角钢,门框中间部分为米字型布置,门框与门板焊接,门板厚度3 mm,防爆门局部结构如图5所示。在应力分析过程中,门框选用Beam188梁结构,防爆门和门框50角钢局部如图6所示。门板选用Shell6+3薄板结构。定义防爆门弹性模量2.06×1011Pa,泊松比0.3,密度7 800 kg/m3。施加运动自由度约束条件:左门框(轴承附件)进行自由度约束,Ux=Uy=Uz=Rx=Rz=0,仅保留y方向的转动自由度。施加载荷包括压力载荷和重力载荷,其中压力是随时间变化的非线性动态载荷,如表1所示。在应力计算中,将流场计算中的24 ms时刻作为初始时刻,建立活动门上所受平均压力与时间的变化关系。与最高压力相比,平均压力更能反映对活动门整体的冲击作用。选择大位移瞬态求解器进行迭代求解。求解控制时间与防爆门总开启时间对应,总时间为0.03 s,时间步长为0.001 s,每一时间步的载荷与压力分析结果对应。
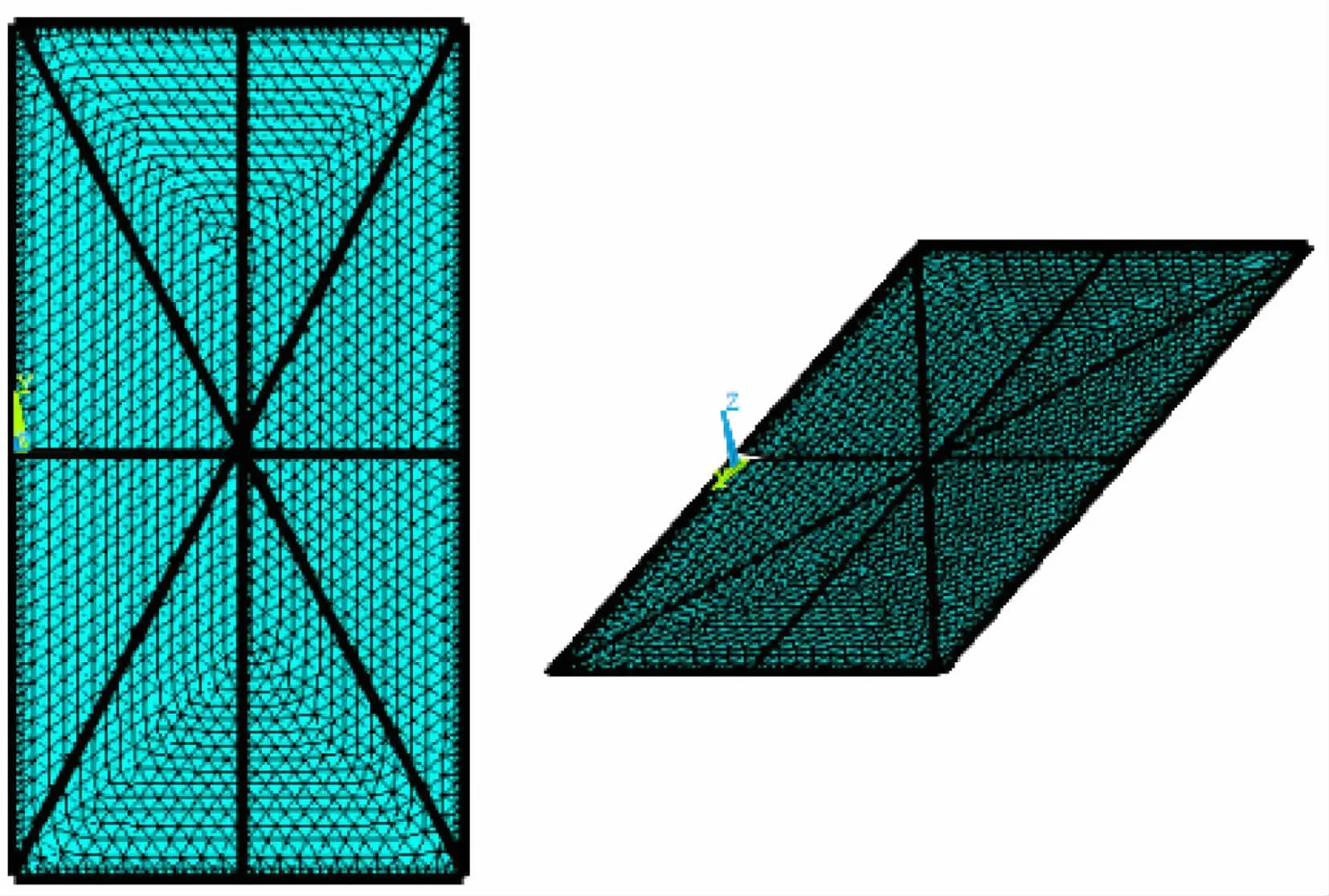
图5 单扇防爆门几何模型Fig.5 Geometric model of single explosion-proof door
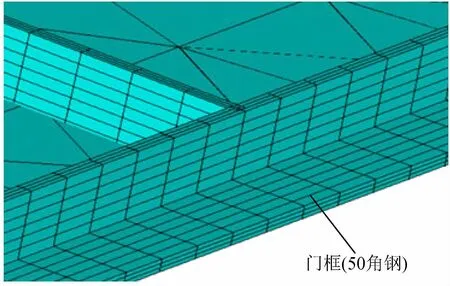
图6 防爆门局部结构Fig.6 Local structure of explosion-proof door
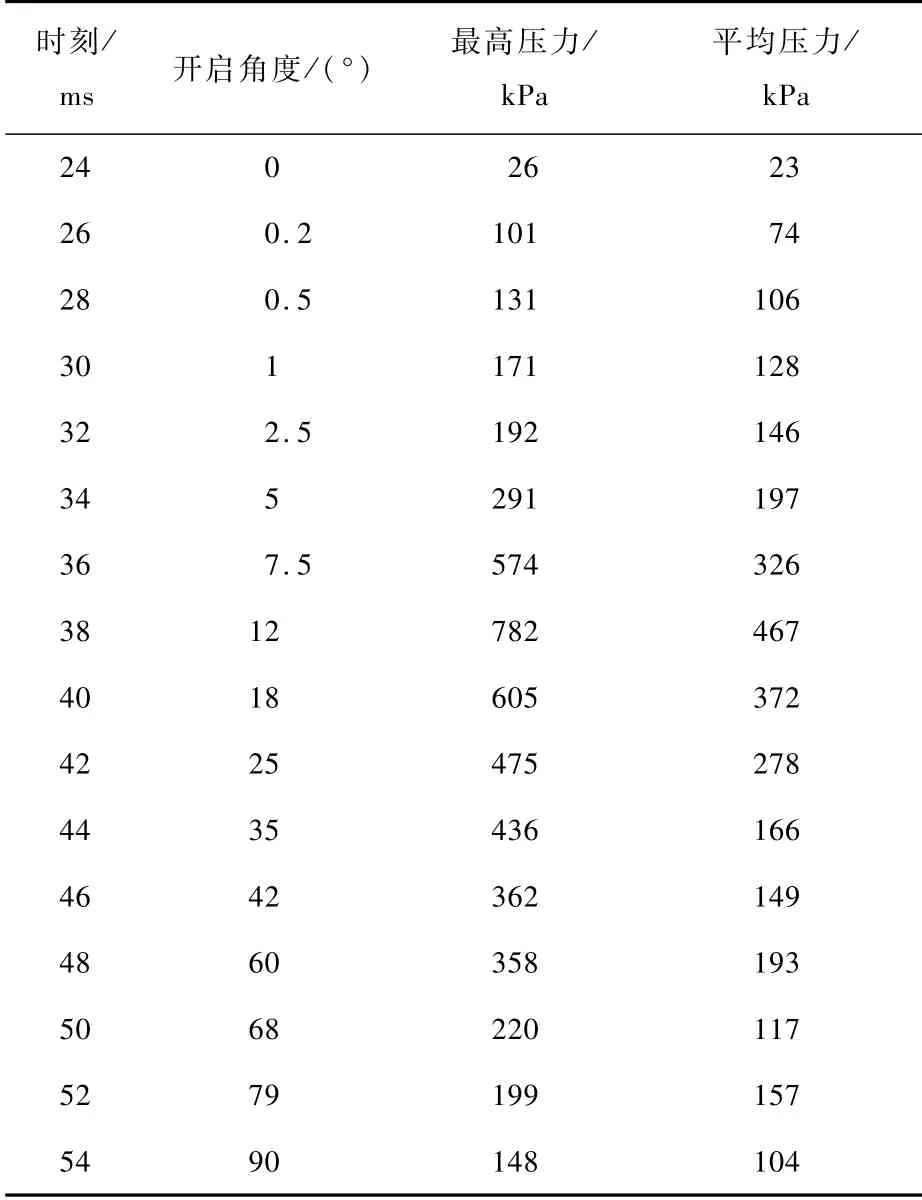
表1 不同时刻防爆门所受的压力Tab.1 The pressures on the explosion-proof door at different time
图7为防爆门的应力分布。可以看出,最大应力为230 MPa,接近钢的许用应力245 MPa;最大变形量为38.9 mm,主要为弹性变形。由于防爆门受到冲击波强大的扭力作用,因此应力集中在防爆门左侧(图7),主要表现为弯曲应力。
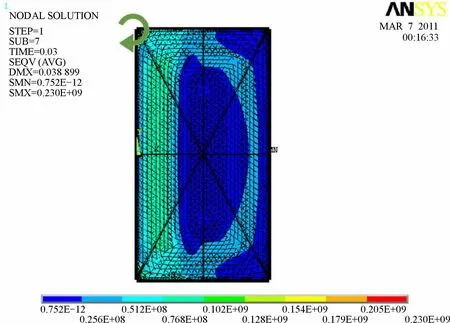
图7 防爆门应力分布Fig.7 Stress distribution of explosion-proof door
4 防爆门结构优化
单扇门在受力运动时除了满足强度要求之外,还需要满足刚度要求。这主要是因为门的刚度不够,会造成门受力发生弯曲变形,使门在再次关闭时出现问题,所以必须提高防爆门的抗弯强度。从以上受力分析可知,防爆门在冲击波压力作用下所受最大应力主要集中在左侧,即靠近转动轴侧附近,因此可在防爆门左侧加装两根加强筋,以进一步降低应力,提高材料安全性。其几何结构和优化后应力分布结果如图8所示。可以看出,结构优化后的最大应力下降为189 MPa,低于钢的许用应力245 MPa,最大变形量为32 mm,未发生塑性变形,说明防爆门结构优化方案合理,防爆门整体可靠性符合要求,优化后效果较好。
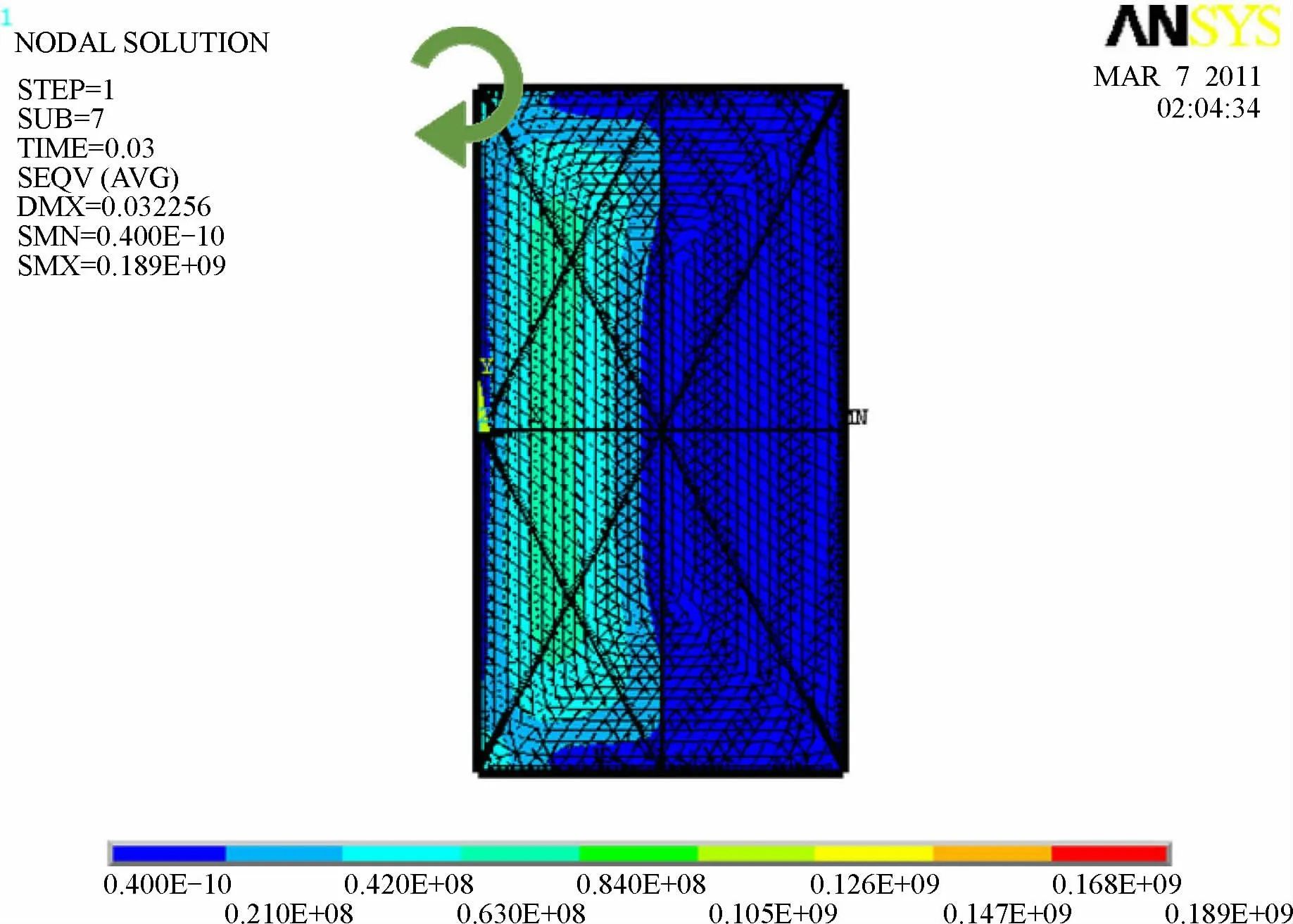
图8 结构优化后防爆门应力分布Fig.8 Stress distribution of explosion-proof door after structural optimization
5 结 论
在防爆门结构设计基础上,利用FLUENT软件对瓦斯爆炸流场进行数值模拟,获得了不同时刻防爆门上的压力分布及其动态响应规律。CH4体积分数9.5%,爆炸冲击波压力为26 kPa时防爆门开始打开,当防爆门开度为12°时压力达到峰值782 kPa。
将不同时刻压力载荷导入ANSYS受力分析软件,进而对防爆门进行动态受力分析,得到了防爆门应力分布,在此基础上进行了结构优化,材料强度校核结果显示优化效果较好,结构优化后的防爆门整体可靠性符合要求。
