基于TOPSIS法和RSR法的江苏省病床使用效率研究

王璐瑶 ，曾智

(南京中医药大学卫生经济管理学院，南京市 210023)

病床作为医院最重要的医疗资源之一，病床的配置是否合理直接影响着医疗活动能否顺利进行，影响着患者的健康保障程度。近年来，国内外很多医院都出现了病床供应不足的压力[1]，尤其是在三级医院经常出现“一床难求”的现象，“看病难”的问题日趋严重[2]。因此，合理配置和有效利用病床资源是医院亟需解决的重点问题，这不仅能够提高医院的工作效率和管理水平，一定程度上也有效缓解了“看病难”的民生问题。本研究利用优劣解距离法(Technique for Order Preference by Similarity to Ideal Solution，TOPSIS)和秩和比法(Rank-sum ratio,RSR)综合评价2020年江苏省13个市的医院病床使用情况，旨在发现存在的问题，掌握各地区之间的差距，为优化病床资源配置，提高利用效率提供参考依据。

1 材料与方法

1.1 资料来源

数据资料来源于江苏省卫生健康委员会发布的《江苏卫生健康年鉴》(2021卷)。选取病床周转次数(X1)、病床工作日(X2)、病床使用率(X3)和出院者平均住院日(X4)4个指标进行综合评价[3]。其中，X1、X2、X3均为高优指标，即该指标对病床使用效率的影响是正向的，指标值越大，越有利于病床效率的提升；而X4为低优指标，即该指标对病床使用效率的影响是负向的，出院者平均住院日越长，病床使用效率越低。

1.2 方法

本研究首先利用Excel录入所有指标数据，通过Excel实现TOPSIS的综合评价过程，然后再运用SPSS 22.0软件确定RSR的分布并求出回归方程和相关系数，最后再利用Excel对综合结果进行排序分档处理。

1.2.1 TOPSIS法。TOPSIS法是一种比较常用的综合评价方法，其基本思想是：对原始数据进行标准化处理后,找出有限方案中的最优和最劣方案,再分别计算各评价对象与最优方案和最劣方案之间的距离,并得出各评价对象与最优方案的相对接近程度,以此作为方案排序的决策准则[4]。目前，TOPSIS法在医疗卫生服务质量评价中被广泛运用[5-6]。本研究根据 TOPSIS 法进行如下处理。

(1)评价指标正向化：本研究四个指标中出院者平均住院日为低优指标，需进行高优化处理，即进行倒数法变换后再扩大100倍[3]。

(3)计算权重值Wj：即为各项指标标准化后的合计数占总和数的比重。

1.2.2 RSR法。RSR法的基本思想是：在一个n×m的数据矩阵中，通过对各指标进行编秩，从而获得无量纲的统计量RSR，根据RSR值的大小对评价对象进行排序[6]。本研究将TOPSIS法和RSR法相结合进行如下处理：

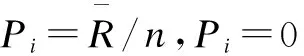
(2)求出回归方程RSR=a+b×probit。

(3)参照《常用分档数及对应概率单位表》要求，对13个地市进行分档排序，从而做出综合评价[8]。

2 结果

2.1 TOPSIS法的评价结果

2020年江苏省13市的病床使用情况如表1所示，病床周转次数(X1)最高为31.4，是扬州市，最低为22.8，是无锡市，除4个市偏低以外，其余市都在28.0之上；病床工作日(X2)最高为300.5，是扬州市，最低为256.3，是连云港市；病床使用率(X3)最高为82.1%，是扬州市，除扬州市和淮安市外，其余均低于80.0%；出院者平均住院日(X4)最高为10.9，是苏州市，最低为8.5，是盐城市。

表1 2020年江苏省13市的病床使用基本情况

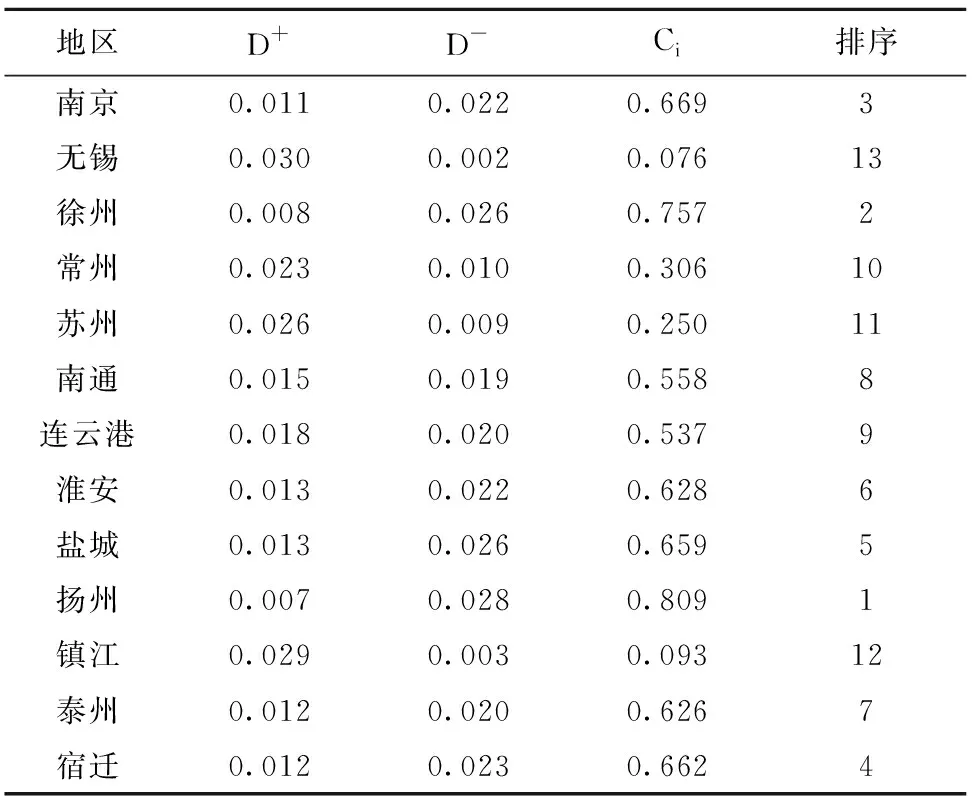
表2 2020年江苏省13市病床使用综合评价及排序

2.2 RSR法的综合评价结果

表3 Ci值的频数分布及概率单位值

2.2.2 回归方程及分档排序。将概率单位Probit值作为自变量，Ci值作为因变量，进行相关和回归分析。结果表明，概率单位Probit与Ci值之间存在线性相关关系(r=0.918，P<0.05)，回归方程为：Ci=0.226Probit-0.657。并对回归方程进行方差分析，认为其具有统计学意义(F=59.321，P<0.001)。

根据《常用分档数及对应概率单位表》[8]，将RSR法分3档的概率单位界值带入回归方程，算出理论Ci值的分档界值，将结果分为优、一般、差三个档次。由分档结果可知，优、差两档的地级市较少，优档为徐州和扬州，差档为无锡和镇江，其余地级市都分布在一般档。根据分档结果计算三档综合评价理论Ci值均值分别为差档0.084 5、一般档0.543 9、优档0.783 0，各档均值差异较大，其中优档是差档的9.3倍[10]。说明江苏省13个市的病床使用效率存在较大差异(见表4)。

表4 江苏省13个市病床使用效率RSR法评价分档情况

3 讨论

2020年江苏省13市的病床使用效率同时存在使用过度和使用不足的现象，并且各地区之间的差异较为明显。由表4的分档情况可见，扬州、徐州等地的病床使用效率较高，处于领先地位；无锡、镇江等地的病床使用效率较低，处于落后地位，其他市的病床使用效率均处于中档水平。

3.1 高效能地区分析

各地区病床使用效率的差异可能是由地区经济发展水平、人口结构和数量、地理位置、卫生资源分布不平衡等因素导致的。以扬州市为例，扬州市病床使用效率为全省最高，但根据2020年江苏统计年鉴结果显示，其平均开放床位数(1.79万张)和每千人口床位数(5.77)均排名全省11[11]。从人口结构来看，扬州市老年人口比重排名全省第3，而老年人对医疗卫生服务的利用远高于年轻人，因此对病床资源需求更大。《全国医疗卫生服务体系规划纲要(2015—2020 年)》中明确规定，到2020年每千常住人口医疗卫生机构床位数(张)要达到 6 张[12]，扬州市为5.77，略低于此标准，资源配置上尚显不足。徐州市人口数量较多(排名第3)，经济发展相对落后(人均GDP排名第11)[11]，且地处苏北，资源配置整体劣于苏南地区[13]，因此病床使用效率较高。而病床开放数量不足、使用率过高、工作负荷较大，可能会导致病床来不及消毒处理，引起交叉感染，带来各种医疗安全隐患，容易造成患者就医感受差、满意度低等现象，甚至会引起医患纠纷[14]。

3.2 低效能地区分析

无锡、镇江等地的病床使用效率较低，这可能与当地的经济发展、地理位置和床位资源配置有关。以无锡市为例，其经济基础好、发展水平较高，人均GDP排名全省第1，资源配置水平较高，每千人口床位数为6.91，排名全省第1[11]。床位配置较多，周转次数较低，可能存在供大于求的情况，导致病床利用效率偏低。此外，病床使用效率低也有可能是这些地区与其他经济发达、医疗水平更高的地区邻近，居民外出就医的比例较高[15](例如：镇江距离南京较近),导致本地区的床位使用效率低。病床使用率过低，开放的床位闲置、冗余，造成了卫生资源的浪费。

4 建议

4.1 将需求和需要相结合，优化病床资源的配置

卫生资源配置具有规模效应和马太效应，大多卫生资源均集中在经济发展水平较高的苏南地区，而苏中、苏北地区经济相对落后，加上基础薄弱、竞争力不足导致获得卫生资源的机会相对较少[16]。因此，政府部门应在考虑各地区的人口数量和结构、经济水平、地理位置等多种因素的基础上，结合各地的卫生服务需要与需求加以综合考量，合理配置病床资源，减少资源的浪费，提高病床利用效率。

4.2 坚持政府主导，鼓励引入社会资本

政府应在卫生资源配置中发挥主导作用，对病床资源匮乏的地区加大经费投入和政策支持；对病床资源配置较好的地区，注重优化结构，提高利用效率；对资源过剩的地区加以管理，并促进资源合理流动，使各地区资源分布保持相对均衡，满足广大群众的医疗服务需求又不至于造成资源的浪费。同时，政府可以鼓励社会资本投资卫生资源薄弱地区，形成多元筹资渠道，既可缓解政府负担，又可以满足人们多元化的就医需求[17]。

4.3 不断提高医疗水平，完善相关管理制度

除了资源配置外，病床周转次数、病床使用率处于较低水平还与医院的医疗水平和内部管理有关[18]。由于诊疗水平不高、诊疗不当，会导致患者延长住院时间，从而也就影响了病床周转次数。同时，诊疗水平低也会导致患者的满意度低和就诊率低，相应地影响了病床使用率。此外，住院流程不合理、门诊与住院之间的工作不协调、出入院安排不够紧凑、病房管理质量较差、各科室间病床配置不合理等都会降低病床利用效率。因此，医院要不断提高医疗水平和服务质量，满足患者的就医需求，为患者提供更优质的服务，从而吸引更多患者就医。另一方面，医院要不断完善相关管理制度，优化住院流程，加强病房管理，协调好门诊与病房工作，优化各科室间的病床配置，努力提高医院管理效率和病床利用效率。

5 研究优势与不足

目前， TOPSIS法和RSR法已被广泛运用于医院管理、卫生政策、整体和部门效益评价等多个领域，其主要优点是应用方便灵活、易于操作使用。TOPSIS法很大程度上降低了极端值对结果的影响，且对样本的数量、数据的分布没有特定要求，能比较充分地利用原有的数据信息。但它也存在一定的缺点：它可以对每个评价对象进行排序，但不能对排序进行分档管理，因此它的灵敏度不高[19]。RSR法不受异常值影响,并可对评价方案进行排序和分档[20]；但在指标值进行秩代换的过程中原始信息损失过大，导致信息不能完全利用，使结果显得不够精确。鉴于此，本研究将TOPSIS法和RSR法相结合，综合评价2020年江苏省13市的病床使用情况，既弥补了TOPSIS法不能分档的缺憾，又避免了RSR法原始信息损失的不足，取长补短，使统计结果更加全面、客观、科学。

本研究仅以江苏省各地级市作为研究样本，但对各市不同级别、不同类型的医疗机构以及同一医疗机构的不同科室之间的差异并未涉及。同时，以地区作为研究样本，在一定程度上反映了不同地区之间病床使用效率的差异，但并未对影响效率的因素进行深入详细的分析，后期还需进一步研究。