从心知到芯知——浅谈测量与计算

陈凯 上海市位育中学

庄子在《应帝王》中以一篇著名的故事来收尾：倏与忽时相与遇于浑沌之地，浑沌待之甚善。倏与忽谋报浑沌之德，曰：“人皆有七窍以视听食息，此独无有，尝试凿之。”日凿一窍，七日而浑沌死。读者在读完之后大概很难这样发问：浑沌是什么？到底是什么死了？因为即便给出答案，所指的必定是已死之物而非浑沌。虽难言浑沌为何，但可猜测庄子想要启示的是世界的本来状态，是那个无为而又能量充盈之所在。从故事中可以看出，浑沌之死与视听食息有关，且倏忽之间就发生了。这多少会让人联想到量子力学中波函数观测即坍塌的神秘特性，或者还会想起那只处于叠加态因观测而命运截然不同的薛定谔之猫。曾有不少作者撰文讨论庄子的浑沌与量子力学之间可能存在的联系，即便其中所说多有穿凿，但既然能够联系到，那至少是存在可联系之物。

从遥远的先秦思想转回到日常生活，这种由观测所造成的坍塌或许无处不在，它和每个人的心灵有关，却需要十分细密的心思去发现。设想某人附庸风雅学习茶道，在茶席之前跪坐品茶，一开始只觉茶水味美，忽觉腿痛且麻，不由喊了一声“痛”。痛和不痛也就在一念之间，跪坐所造成的腿痛慢慢累积，直到这个人意识到这种痛，当他意识到这个“痛”的时候，此“痛”就不再是未意识到的“痛”本身，根据科学研究的结果，主观情绪会改变痛的感觉，所以说，痛的浑沌在痛被观测到的倏忽之间就成为意识中的另一种痛。而当旁边的听者听到那一声“痛”的时候，这个“痛”又变换为一个离散的信号，是绝不可能让听者真实还原出那种“痛”的现场感受的。唐代裴休在《黄蘖山断际禅师传心法要》中说“明於言下忽然默契……如人饮水，冷暖自知”，这种“自知”是感觉的私有领域，无法与他人言说，且每一次感知都实质上导致水温的变化，所谓的真实状态永远隐藏在感知动作的倏忽之前。

人们研究生物体的结构与工作原理，并据此发明出新的设备和工具，人们在设计自动计算装置之初，便想要借助对人的头脑的仿生来实现这些装置。这个想法看上去合理，但实际尝试却是困难重重。首先，人脑神经元的信号传递兼具连续和离散的特点，其工作方式如何与人的决策行为关联，至今仍有诸多未解；其次，如神经元那样的信号传递方式的再现也颇为困难。数字计算机的广为使用当然是巨大的成功，但这也可以看成是无法从底层功能模拟人脑运行机制的一种妥协。虽然当前信息技术学科教学总是要围绕数字计算机的软硬件来开展，但学习者也应该在“何以如此”这样的发问过程中得到思维的成长。譬如，对某简单的程序代码“a=3;b=a;print(a);print(b)”这般发问：a和b本质上是什么？3又是什么？b是怎么得到3的？b得到3后a还能保持原样吗？如何让人知晓a和b所代表的数字？看似无理取闹的问题背后往往另藏玄机，在诸多问题中，本文暂且只关注如“b=a”这种语句中所隐含的测量问题，如果用颇为专业的遣词琢句来描述“b=a”，当称为“将变量a的值赋值给变量b”，试着将此描述解构并以展现出语句如何可行的目的而对其进行重组后，这种描述可能是“获知用a符号所代表的数字，并将b符号所代表的数字使其与a符号一致”。在这看似如此简单的给变量赋值的过程中，在机器底层又是如何做到那所谓的“获知”的，一个赋值语句其实隐含了测量的问题。若仅仅满足于知晓“b=a是一句赋值语句”这样的道理，那就是满足于当前枝杈上的果实，却错过回溯到树枝分叉处，寻得新的分枝的可能。

● 用测量来计算的方法以及计算精度

在一定精度要求内，用测量的方法来实现计算是可行的，如用计算尺计算3.2乘以2.2，计算尺采用了对数运算的原理来实现乘法运算的一定程度的自动化。大家如手边没有计算尺，可以利用网络上的计算尺模拟器（很容易通过slide rule simulator关键字搜索到）来实施计算模拟，简单滑动计算尺，就可以获得结果，如图1所示。可以从游标的位置看出，这个结果大于7，小于7.1，但游标所指向的位置到底是什么呢？因为两个参与运算的数字末尾都是2，所以可以推算出结果7.04。虽然理论上说，可以用计算尺计算有更多小数的数字的乘法，如3.216乘以2.214，但就算十分小心地移动滑尺，也不可能得出7.120224这样精确的结论。神奇的是，只要操作足够小心，还是能知道这个乘法的结果略大于7.12。

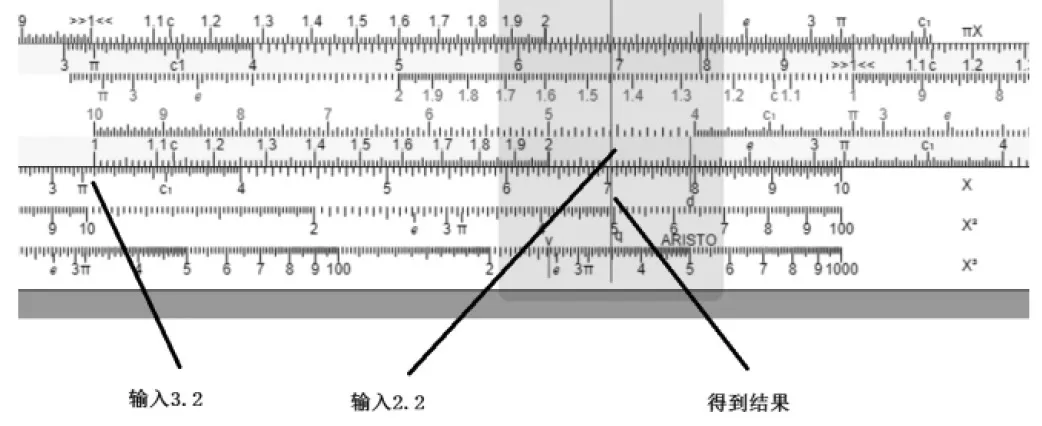
图1 用计算尺进行乘法运算

计算尺是不是一个自动计算装置？从某种意义上说可以算是，它获取了输入数据，并自动给出输出数据。按这样的思路，一个有刻度的量杯也可以算是能够实现自动加减法运算的自动计算装置了。不过此类装置都存在一个大问题，它依赖人的观测，这导致了两个后果，其一是必然存在的误差，其二是运算结果不能自动用于新一轮的运算，而需要由人来再次实施数据输入的动作。在一个复杂的自动计算系统中，观测者不是人而是某器物。

● 观测者的影响

因为只是看了一眼对象，就改变了对象的状态，这样的事情不只发生在微观粒子上，用于计算的装置中也有类似的情况。例如，有某个用电容来储存数据的装置，数据的读数就是电容的电量，每次打开开关读取数据，电容的电量就下降一些，观测得越多，距离原来的结果就越不准确。图2所示的是使用电流表来检测电容电量的情况，在这个电路中，首先断开2号电键，闭合1号电键给电容充电，这样，电容中电量多少的程度就可以用来代表特定的数据，然而，想要知道这个数据到底是多少，就必须进行检测，在检测时，1号电键是断开的，短暂闭合2号电键，从电流表中就可以读出电流量。然而问题是，每一次检测就造成电量的流失，这也意味着数据的损失。

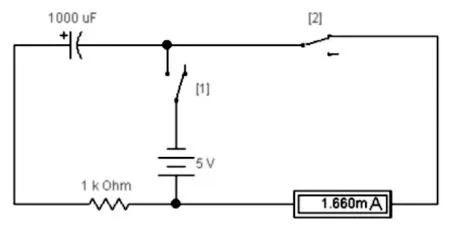
图2 通过电流表检测电容的电量

另一种方法是借助电压来获得信号的数据，如图3所示，首先断开2号电键，闭合1号电键给电容充电来存储数据，其后就可以通过检测电压的方式获取数据，但每次测试，电压数据都会下降一些。

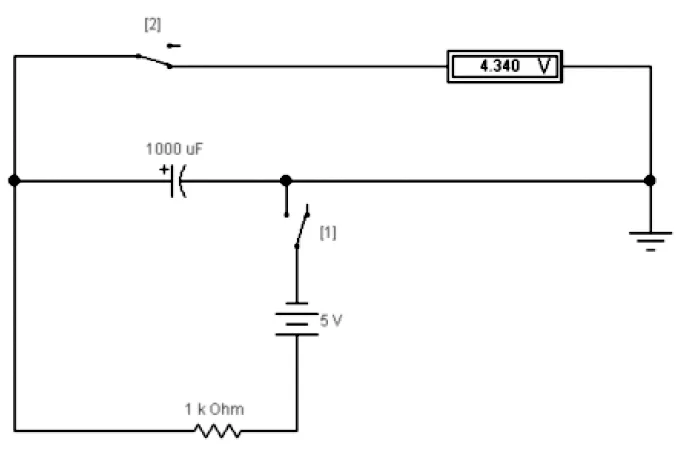
图3 通过电压表检测电容的电量

相比而言，采用检测电压的方式获取数据，比检测电流的方式损耗要小得多，这是因为检测电压的设备旁路于被测系统，只有很少的电流分流到检测设备中，不过这带来了另一个问题，这样获得的电信号无法驱动功率稍大一些的设备，限于篇幅本文暂不讨论。

即便对于一个稳定的对象，如将电容替换成一个理论上电量不会变化的电源，只要检测设备接入到系统中，获得的数据就已经不准确了。图4是数据获取中存在误差的一种证明。

图4 观测设备获取数据过程中产生误差

● 消除观测误差与量化

如果观测时的误差是必然的，那么，不妨将数据连续变化的范围分为不重叠的若干个子区间，每个子区间用一个确定数值表示，落入其内的信号就以该数值来输出。大家难免会联想起数字计算机在模拟信号输入时所做的采样和量化。设想一下，教师可能会对“为什么要实施量化”这样的问题回答道：“为了将数据编码成数字计算机可处理的二进制代码的形式。”这样的回答当然是对的，但却没有揭示出技术思想进化的源头，正如地理上真正存在的大江大河，它是由许多支流汇聚而成的，量化这个工具的成型，有其众多的思想源头，为消除观测带来的误差而产生出的方法，是其中一个源头。试举一例，图5是帕斯卡加法器内部结构示意图，它由许多齿轮组成的，齿轮的齿的转动的位置是连续平滑的，但借助连杆和独齿的结构，当转动个位数上的齿轮后，只有个位数上的数字有可能存在模棱两可的情况，而从观测窗口中所看到的十位上的以及更高位上的数码的符号在每个时刻都是唯一的。

图5 帕斯卡齿轮加法器原理

如果转动齿轮的不是人，而是持续流动的水流，那么用类似的齿轮装置就能够观测水流量的多少了。个位数上齿轮的转动真正匹配了水流量，但却难以精确读取，十位以及更高位上的齿轮能够很清晰地被读取，但不完全匹配水流量，不过，它们的数值还是能基本对应水流量变化的一定区间。生活中，当水表读数以表盘的指针形式呈现时，人们通常不会去读（因为很难读出）最小位的指针数据，这其实就隐含了用量化的思想来解决问题的方法。将这个齿轮加法装置视作系统，误差只是在外部状态输入到系统内部的边界上发生，而在系统内部，齿轮转动具有离散的特点，误差不再持续产生。产生开关量信号的电路是量化的一种极端的例子，如某种很常见的光敏传感器，当环境光弱时输出高电平信号代表开关量数据1，环境光强时输出低电平信号代表开关量数据0。

● 消除观测带来损耗的思路

设想一下，用齿轮加法器测量水流量会存在这样的问题，如果需要记录的数据的位数很多，则需要用到的齿轮组也很多，那么，当连杆推动齿轮时的摩擦和阻力就有可能造成数据记录的误差。为了避免这种情况，可以想象采用这样的方法：每一个数位上的齿轮都得到一定量的水流冲击，但这种冲击本身不足以推动齿轮，只有当来自低位齿轮的连杆的推动结合自身位置上原本的水流冲击，才能推动齿轮前进一格。这个方案解决了两个问题：其一，它保证计算系统内部的数值一定处在某个量上；其二，它避免了内部模块中的误差在信号传递过程中逐级累积起来。

在考察真实的电子电路的计算装置如何解决问题之前，不妨先来看一个抽象的软件模型。假设有某个Python的编译环境，在变量之间不允许使用“=”符号来赋值，也就是说，虽然允许执行“a=3”，但“b=a”这样的语句是不允许出现的，可以使用的只有教师事先自定义的get函数和put函数（自定义函数内是可以使用“=”的，但可以设定规则，要求不能修改函数），get函数从一个列表中获得数值，不过，在获得数值的时候，列表中的数值就会随机减少一定量，显然，get动作做得越多，数值距离原始的值就越不准。而put函数的作用是向某个列表存入某个数值。相关代码如图6所示。程序运行后可知，即便列表中原来存储数值是10，只要将其赋值给另一个列表，那么这个数值就会随机减少一定量。所以，需要思考在这种情况下如何做到准确地在列表之间传递数据。

图6 自定义函数get和put

应当如何消除这种随机数据减少而带来的影响呢？可以试着将发生偏差的数据用量化的方法来使其归位。具体实现也很简单，可以设定一个阈值，用分支语句判别输入数据是大于还是小于阈值。可以发现，将数据量化为0和1两个二进制数码，实现起来最为容易。代码如图7所示，从表面看是变量间传输了两个数字10，但实际上，程序代码的作用是在变量间传递二进制数11，也就是十进制数3。

图7 在一个存在数据损耗的系统中准确传输数据的模拟

● 观察电路的行为并猜测芯片的行为

现实中的计算装置为解决观测时所产生的数据误差和损耗的问题，与上述函数模型的行为有一定的相似。图8所示的是一个可以互动的实验装置，既可以实际搭建出来，也可以只在面包板模拟器上模拟其行为。装置中的4069是一种非门芯片，它的功能就是检测开关量信号并取反输出。笔者试图借助这个互动实验装置，将简单的功能需求背后隐藏的复杂行为揭示出来：其一，通过光敏电阻的变化可以看出，4069芯片内部存在一个阈值，根据这个阈值将输入的电压信号归入0和1这两个量，并取反输出；其二，无论输入情况如何，芯片输出的信号都采用尽可能高的电压和尽可能低的电压表示1和0这两个量，这样，芯片之间数据的传输就具有了一定的抗干扰能力，可以通过调整干扰电阻的阻值在两个芯片的信号传输线路上施加电压上的干扰，来验证芯片具有一定程度的数据“归位”能力。

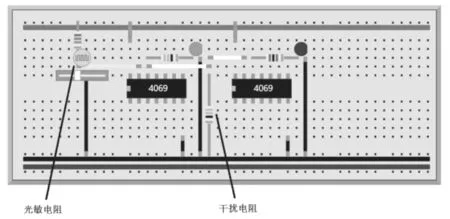
图8 4069芯片的数据输入与输出实验

除去4069芯片自身特有的取反功能，其获取数据和输出数据的行为与之前用Python自定义的get和put函数的行为是非常类似的。显然，真正的底层电路不可能是因为程序代码而产生出此行为，那么，这种能将数据回复和归位的行为是如何实现的？另一个值得深究的问题是，无论怎样调整干扰电阻的阻值，只能影响右侧芯片的工作，而不会影响左侧芯片的工作，在电路中，正是左侧芯片通过输出引脚，将数据传输给右侧芯片，可以说，观测者对被观测对象的影响被降到了极低的水平，那么，使得芯片有此行为的底层原理又是怎样的？这些问题的解决都需要进一步将芯片解封才有可能知晓，那将是另一段值得探索的旅程。