基于改进型状态变量控制算法的再热汽温控制研究
2022-09-01倪向红范常浩易秉恒
陈 刚,倪向红,范常浩,胡 勇,易秉恒
(1.国能南京电力试验研究有限公司,江苏 南京 210023;2.华北电力大学控制与计算机工程学院,北京 100085;3.国能(泉州)热电有限公司,福建 泉州 362804 )
1 引言
状态变量控制算法作为一种事前调节手段经常被用来解决大惯性时滞系统的控制问题[1-9],通过建立控制对象的数据模型提前预判控制对象的变化情况,让调节器提前动作进而起到事先调节的作用。由于算法原理与物理过程的紧密联系,使其成为先进算法中易于被工程人员理解并掌握的控制算法,例如火电厂再热汽温控制中就常用到状态变量控制技术。
针对状态变量控制技术的理论研究和工程应用,诸多专家学者进行了大量研究。文献[10]由锅炉蒸汽流程关联状态观测进而提出应用状态变量控制技术进行单级再热汽温控制的构想。文献[11]将状态观测得到的汽温变化量引入调节器的前馈环节,实现对再热汽温变化的超前调节。文献[12]提出基于Hammerstein模型的增量式函数观测器IFO-KΔx,通过理论推导得出增量式观测器IFO-KΔx的鲁棒性要优于鲁棒Luenberger观测器,并且具有较大的稳定裕度。文献[13-15]用状态空间方程对状态变量控制进行数学分析,并通过使性能指标函数最优的方法计算得出状态系数矩阵,最后根据艾克曼公式和对偶原理计算出状态观测器的增益矩阵。文献[16]将增量式状态变量控制器应用于W形火焰直流锅炉过热汽温控制。文献[17]将基于线性矩阵不等式(linear matrix inequality,LMI)方法的线性时滞系统鲁棒H∞控制技术应用到电站锅炉再热汽温控制中。可见,状态变量控制技术在解决大迟延、大惯性对象自动控制问题具有明显优势,但大多研究仅限于理论推到和仿真试验,并未真正实现工程应用。
为有效解决再热汽温自动调节效果欠佳的问题[18-22],提出一种改进型状态变量控制算法,采用等效传递函数法计算状态反馈增益矩阵,采用状态空间方程极点配置法计算状态观测增益矩阵,其次通过仿真试验分析状态变量反馈回路对于控制对象动态特性和开环增益的补偿作用,控制效果优于传统PID控制,将其应用到某电厂660MW超临界机组再热汽温控制系统中,汽温控制效果得到明显改善,大大提高了自动投入率。
2 算法分析
2.1 改进型增量式状态控制变量算法
典型状态控制变量算法是以调节器输出作为控制算法的输入,由于调节器的输出一般不为零,此时用带有静态参数的传递函数表征控制对象,而静态参数在不同负荷工况下均不同,精确获取这种带有静态参数的传递函数难度较高,所以典型状态控制变量算法在工程应用时有一定难度。实际现场一般是根据系统输入和输出的变化获取控制对象的传递函数,由此提出一种改进型的增量式状态变量控制算法。控制算法结构示意图如下。
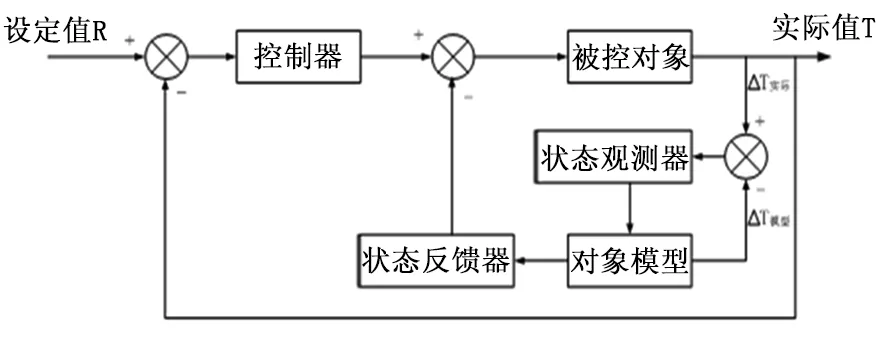
图1 增量式状态变量控制算法结构示意图Fig.1 Structure diagram of incremental state variable control algorithm
根据火电厂再热汽温控制系统汽水流程[27-30],可列出调节器输出(再热汽温减温水调节阀指令)与再热器出口汽温(以下称出口汽温)的关系为:

(1)
式中:△U为调节器输出变化;△T0为出口汽温变化;K为调节器输出与出口汽温传递函数增益;T为调节器输出与出口汽温传递函数惯性时间;m为调节器输出与出口汽温传递函数阶数;S为拉普拉斯变换算子。传递函数中待定参数可通过再热器减温水调门特性试验获得。
△U和△T0可列分解式如下:
△U=Uk+P-Uk
(2)
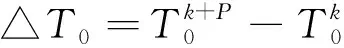
(3)

根据上述关系式设计出改进型增量式状态变量控制算法如下(式(1)中m=4)。
2.2 状态反馈增益矩阵
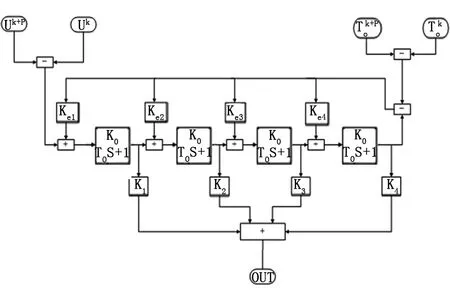
图2 改进型增量式状态变量控制算法Fig.2 Improved incremental state variable control algorithm
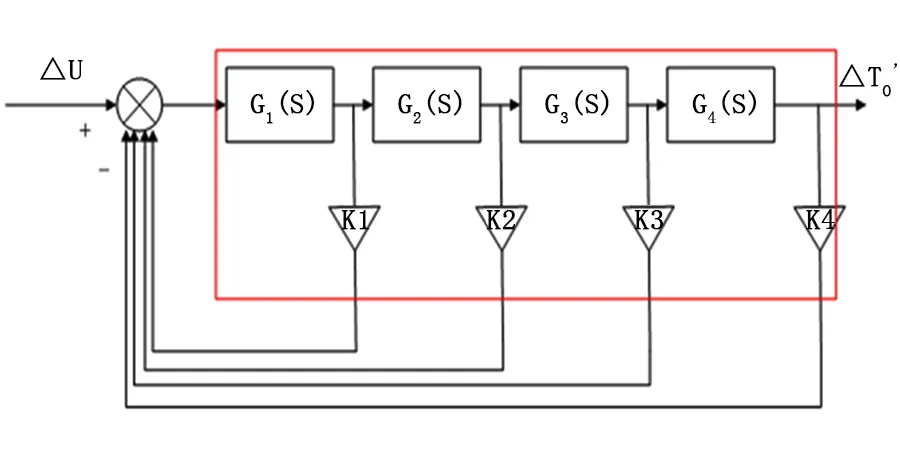
图3 4阶改进型增量式状态反馈结构图Fig.3 Structure diagram of fourth-order improved incremental state feedback
将图3中方框内结构用等效传递函数Ge(S)表示(以下简写为Ge),定义其表达式为
(4)
式中:K0为等效传递函数增益;T0为等效传递函数惯性时间;β为压缩因子,其大小反映状态反馈对系统的加速程度,取值范围为0<β<1。
实际系统的传递函数Gi一般不完全相同,为应用等效函数法此处可将其简化为式(4)形式,由于控制算法的鲁棒性,据此计算出的状态反馈增益矩阵完全能够满足工程应用要求。
图3方框内结构可以直接表示为:
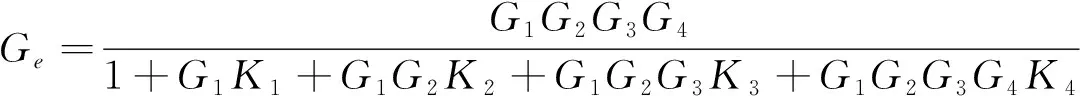
(5)
将Gi表达式代入(5),则有:
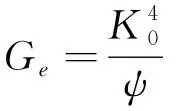
(6)
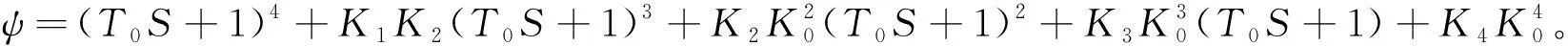
将式(4)按牛顿二项式定理展开并与式(6)比较,可得:
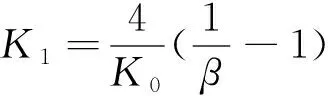
(7)
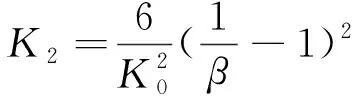
(8)

(9)
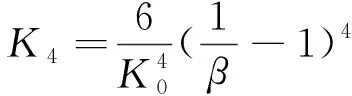
(10)
进一步推广可得状态反馈增益的一般计算式:
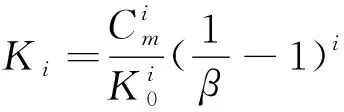
(11)
2.3 状态观测增益矩阵
图4观测器的状态空间表达式可写为:

图4 4阶改进型增量式状态观测器状态空间结构图Fig.4 State space structure diagram of fourth-order improved incremental state observer
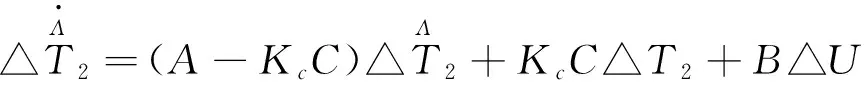
(12)

(13)
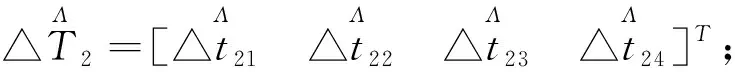

(14)
代入式(12)和式(13)可得:

(15)
f(S)=det[SI-(A-KcC)]
=S4+a1S3+a2S2+a3S+a4
(16)
其中ai为T0、K0、kci的多项式。
再取负实部的期望极点,由此构成期望特征多项式:
f*(S)=S4+b1S3+b2S2+b3S+b4
(17)
其中bi为常数。将式(16)与(17)对应系数比较即可计算出Kc。需注意Kc的大小决定对象模型输出收敛于实际对象的速度,Kc过大时就会放大噪声干扰从而影响系统的稳定性。
3 仿真试验
3.1 状态反馈回路的补偿作用
选取某电厂660MW超临界机组的再热汽温对象模型进行仿真试验,其传递函数为:

(18)
根据式(11)计算状态反馈增益,其中压缩因子βi(i=1~5)分别取0.1、0.25、0.5、0.75、0.9,经计算状态反馈增益矩阵分别为:
K1=[30 337.5 1687.5 3164.06];
K2=[10 37.5 62.5 39.06];
K3=[3.33 4.17 2.31 0.48];
K4=[1.11 0.46 0.086 0.006];
K5=[0.37 0.051 0.00318 7.35e-05]。
为分析压缩因子β对系统动态特性的补偿作用,将β取不同值时分别进行仿真系统的单位阶跃响应。系统不同响应情况如下图,其中β=1时为不经过状态反馈补偿的原始系统。由图5可以看出状态反馈可以减小系统的开环增益及稳态时间,其中β取值过小时(β取0.1或0.25时),系统增益过小不利于调节器参数整定;当β取值在0.5至0.9之间系统特性改善的同时也便于调节器参数整定。
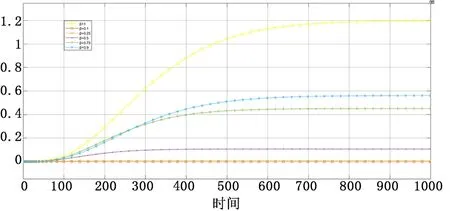
图5 β不同取值时状态反馈补偿作用对比图Fig.5 β Comparison diagram of state feedback compensation effect under different values
3.2 算法控制仿真
增量式状态变量控制技术与PID调节器联合使用效果较好,改进型算法也同样可以与PID算法联合使用,并且使用方法完全一致,有所区别的是式(2)与(3)中的变化时间间隔P的参数选择对控制效果有一定影响,P的取值可参考系统近似纯延时时间。控制对象传递函数为式(18),状态反馈增益矩阵K=[7.53 5.24 3.20 2.07],状态观测增益矩阵Kc=[0.85 0.8 0.65 0.55],P=25。分别采用改进型增量式状态变量—PID控制与常规PID控制的系统阶跃响应情况对比如下图,从图中可以明显看出改进型增量式状态变量—PID控制动态响应时间和超调量指标均优于常规PID控制。
4 现场应用实例
选取某电厂660MW超临界机组作为工程应用平台,该机组A、B两侧再热汽温通过再热器减温水调节阀调节。机组自投产以来,由于常规PID控制算法无法实现再热器减温水调节阀自动控制,日常运行过程中再热汽温的调整主要通过运行人员手动调整,调节方式比较粗放,汽温调节效果欠佳。
将改进型增量式状态变量—PID控制算法应用于本台机组再热汽温控制系统后,再热汽温控制效果得到明显改善,如下图所示。
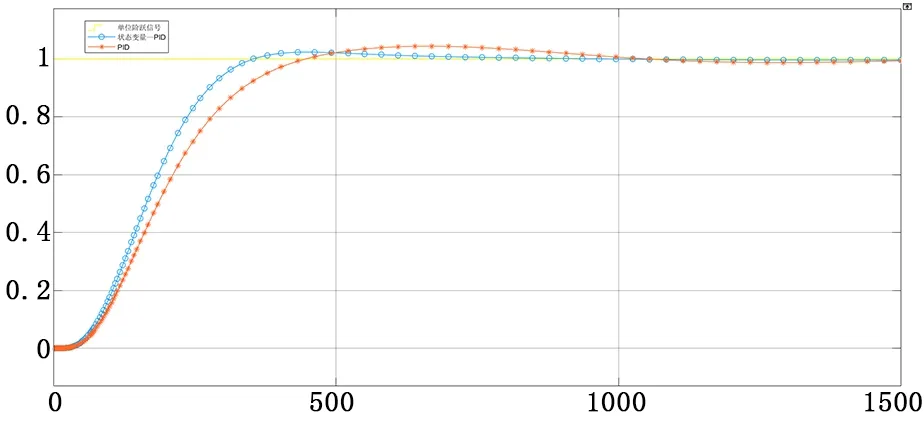
图6 改进型增量式状态变量—PID控制与常规PID控制的阶跃响应比较图Fig.6 Comparison diagram of step response between improved incremental state variable PID control and conventional PID control
对以上试验过程分析:
(1)由图7可知,A侧再热汽温设定值正向阶跃改变5℃,则再热汽温实际值调节时间为12min,最大超调量为1.2℃,则稳态偏差小于±0.5℃;设定值负向阶跃改变5℃,则再热汽温实际值调节时间为11min,最大超调量为1.2℃,且稳态偏差小于±0.5℃。
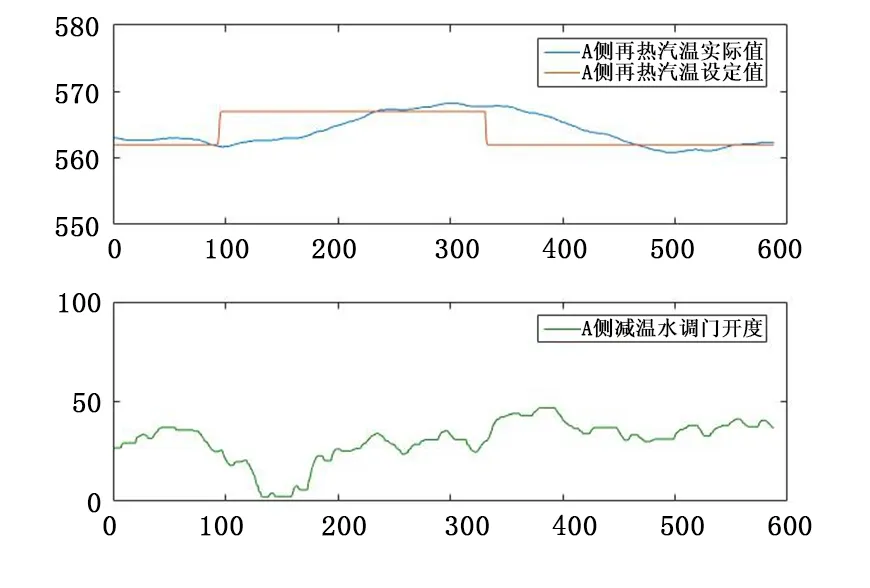
图7 A侧再热汽温定值扰动试验Fig.7 disturbance test of reheat steam temperature on side A
(2)由图8可知,B侧再热汽温的设定值正向阶跃改变5℃,则再热汽温实际值调节时间为12min,最大超调量为1.2℃,稳态偏差小于±0.5℃;设定值负向阶跃改变5℃,则再热汽温实际值调节时间为14min,最大超调量为0.6℃,且稳态偏差小于±0.5℃。
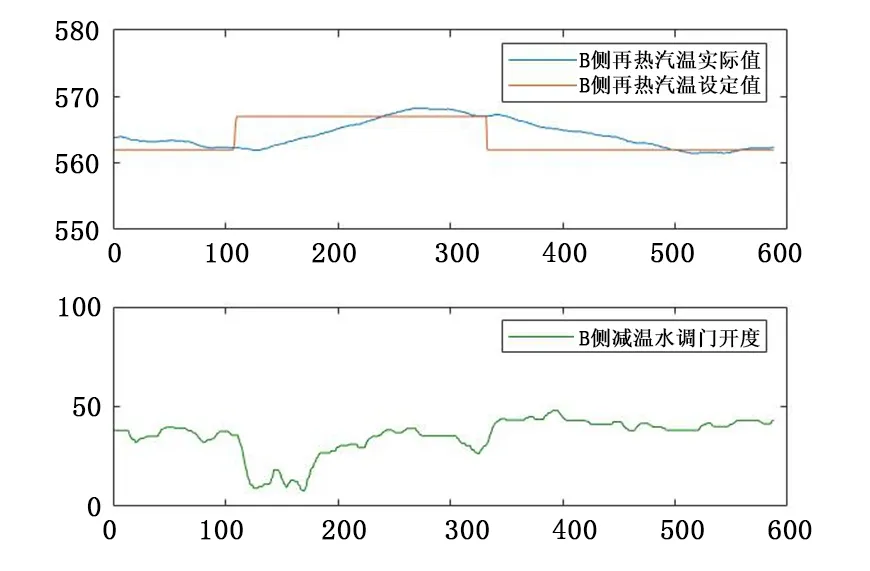
图8 B侧再热汽温定值扰动试验Fig.8 disturbance test of reheat steam temperature on side B
通过采用改进型增量式状态变量—PID控制算法优化再热汽温控制系统,可以减少调节时间,降低过程超调量,减小稳态偏差,有效提高再热汽温调节品质,各项调节指标均由于相关规程要求。
5 结 论
(1)针对再热汽温大迟延、大惯性特性,从典型状态变量控制算法和一般增量型状态变量控制算法工程应用的局限性出发,提出一种结合二者优点的改进型增量式状态变量—PID控制算法,并采用等效传递函数法和极点配置法分别对状态反馈增益矩阵和状态观测增益矩阵进行推导,控制器参数的计算方法更易于工程人员理解掌握。
(2)通过研究压缩因子对系统开环增益及稳态时间的影响,得出压缩因子的合理取值范围,为工程人员对其数值的选取提供参考。
(3)改进型增量式状态变量—PID算法可实现再热汽温的优化控制,对生产过程中其余大惯性时滞系统控制问题的解决也具有借鉴意义。
