基于时延分析和IMA-ELM的出口SO2浓度预测

李 健，王 东，王 瑞，尚星宇

(国家能源集团科学技术研究院有限公司银川分公司,宁夏 银川 75001)

1 引言

随着经济社会的发展，火电行业面临着增加供应和减少碳排放的双重挑战，“双碳”目标下，煤电改造迫在眉睫[1-2]。煤在我国能源结构中占据着主要地位，由于其燃烧时会释放出大量的SO2气体，对大气环境造成污染，因此需要对燃煤产生的烟气进行净化处理[3]。“三改联动”背景下，针对煤电排放改造提出更高要求，新型电力系统下燃煤机组脱硫方法仍然是研究热点。

燃煤机组目前主要采用的烟气脱硫方法为石灰石-石膏湿法脱硫，该方法具有脱硫效率高，使用成本低等优点[4-5]。但在实际生产中，由于脱硫系统受机组负荷波动影响较大，其内部反应也较为复杂，因此很难实现对出口SO2浓度的稳定控制[6-7]。建立关于出口SO2浓度的预测模型，不仅可以帮助运行人员及时调整脱硫系统相关参数，提高脱硫效率，还可以提高整个脱硫系统的控制水平，降低脱硫的成本。

随着人工智能的快速发展，越来越多的机器学习算法被广泛应用于烟气浓度预测。崔仕文等[8]利用最小二乘回归对输入变量进行分析，将影响较大的因素作为输入变量，利用支持向量机(Support Vector Machines, SVM)建立了关于脱硫效率的预测模型，取得了良好的预测效果。苏翔鹏等[9]利用径向基函数(Radial Basis Function, RBF)神经网络对SO2排放量进行建模，通过与误差反馈 (Back Propagation, BP)神经网络进行对比，突出了RBF建模的优势。虽然浅层神经网络能够部分对象进行建模预测，但受其结构限制，模型预测精度难以进一步提升。深层神经网络由于其强大的学习能力和非线性拟合能力，近年来吸引了众多学者的关注。金秀章等[10]利用套索(Least Absolute Shrinkage and Selection Operator, LASSO)算法对初始辅助变量进行了筛选，利用长短期记忆(Long Short-Term Memory, LSTM)神经网络搭建了出口SO2浓度预测模型。马双忱等[11]将LSTM与线性整流函数层(Rectified Linear Unit, ReLU)相结合，搭建了关于脱硫系统浆液PH值、脱硫效率的深度神经网络预测模型，探究了湿法脱硫系统各个参数指标对脱硫效果的影响。虽然深层神经网络模型具有很高的预测精度，但考虑到其计算量大，训练时间长等缺点，很难应用于实际生产中。极限学习机(Extreme Learning Machine, ELM)是在传统神经网络的基础上改进而成的一种前馈神经网络，它具有拟合能力强，泛化精度高、训练速度快等优点。Wang等[12]利用深度神经网络(Deep Neural Networks，DNN)从数据中提取有效信息，利用ELM建立预测模型，实现对脱硫系统出口SO2浓度的有效预测。程琳等[13]利用遗传算法对ELM相关参数进行优化，建立了SCR脱硝系统预测模型，有效预测了SCR出口NOx质量浓度变化。

由于湿法脱硫系统内部反应需要一定的时间，因此从DCS上采集的数据其输入与输出变量间存在着时间延迟，为了保证模型的合理性，需要对输入变量进行时延补偿。目前时延分析最常用的方法为滑动窗口法，即通过比较不同时刻内输入变量与当前确定好的输出变量之间的相关性，从而确定最佳的迟延时间，进而对输入变量进行时序上的调整，实现时延补偿。用于衡量两组变量间相关性大小的指标有：皮尔逊相关系数[14]( Pearson correlation coefficient)、互信息[15](Mutual Information，MI)、最大信息系数[16]等。但上述方法只考虑到了系统由于内部自身原因导致的时间延迟，没有考虑到不同工况下烟气流速变化可能导致延迟时间产生变化。

综上所述，提出了一种基于时延分析和蜉蝣算法优化极限学习机的出口SO2浓度预测模型。首先利用互信息计算不同时刻内输入变量与输出变量间的相关性大小，从而确定最佳延迟时间，考虑到工况变化可能会导致延迟时间发生变化，因此设计了一种可以实时更新的时延补偿方法。利用蜉蝣算法对原始输入变量进行寻优，从而确定与ELM模型相匹配的最优特征子集。最后利用蜉蝣算法优化ELM模型的相关参数，通过与其他机器学习建模方法进行比较，证明了ELM模型预测精度最高，能够对出口SO2浓度进行准确预测。

2 研究方法

2.1 极限学习机

极限学习机是2004年南洋理工大学黄广斌提出的一种前馈神经网络[17]。

ELM的网络结构主要由输入层、隐含层和输出层组成。输入层的神经元个数根据模型输入变量的个数来确定，隐含层神经元个数可由优化算法得出。输入层与输出层的连接权值为w，隐含层节点上的偏差为b、w和b可以通过随机产生获得，也可以通过寻优确定。隐含层与输出层的连接权值为β，如果设隐藏层的输出为H(x)，则可以得到H(x)的计算公式如下所示：

H(x)=[h1(x),…，hm(x)]

(1)

式中：hi(x)表示隐含层第i个结点的输出，其计算公式如下；

hi(x)=g(wix+bi)

(2)

式中：g表示激活函数。

输出层通过连接权值β最终得到整个ELM的输出值f(x)：

(3)

输出层的权值β可以通过求取最小化训练误差得到，因此ELM的训练过程其实就是对输出层权值β的求解过程，其目标函数如下：

min||Hβ-T||2

(4)

式中：T为目标矩阵。

2.2 蜉蝣算法原理及其改进

蜉蝣算法是2020年最新提出的一种群智能优化算法，它通过模仿蜉蝣种群中的求偶和交配行为使得算法最终收敛于全局最优值[18]。在原始蜉蝣算法中，初始种群个体主要通过随机产生，但这种随机得到的个体由于其自身的不确定性，使得算法在迭代的过程中种群的多样性不断下降，最终陷入局部收敛。针对这一问题，本文提出了一种基于反向学习的初始化种群策略[19]。具体流程如下：

(1)首先随机产生一个初始种群，然后根据这个初始种群生成它的反向种群。

(2)计算两个种群每个个体的适应度并排序，分别从两个种群中挑选一半适应度较高的个体，组成新的种群。

(3)将得到的两个新种群分别作为雄性蜉蝣和雌性蜉蝣的初始种群并应用于寻优算法中。

通过这种反向学习可以使得种群个体均匀地从全局产生，避免了算法在迭代过程中陷入局部收敛。同时通过选取适应度较高的个体，减少了种群与最优解之间的距离，加快了算法的收敛速度。

由于湿法脱硫系统内部反应需要一定时间，因此采集的数据中输入变量与输出变量间存在着时间延迟。通过时延分析可以对输入变量进行时序上的调整，从而提高输入变量与输出变量间的对应关系，保证所建模型的合理性。传统时延分析方法主要通过计算不同时刻内输入变量与输出变量间的相关性大小来确定延迟时间[20]，但由于湿法脱硫系统的特殊性，传统方法存在以下两个缺点：一是在湿法脱硫系统中单个输入变量不仅与输出变量相关，也会收到其他的输入变量以及设备和人为控制等影响。二是不同工况下烟气流速不同，可能会导致相关变量的延迟时间发生改变。针对上述缺点，提出了一种基于互信息的改进时延分析方法：

(1)首先选定一组输入变量与输出变量，计算两组变量间的互信息。互信息可以反映两组变量间非线性相关性的大小，对于描述两组变量间整体变化趋势是否一致也更加准确可靠。

(2)由于脱硫塔内最大反应时间不超过十分钟，因此设置时延上限为600s，分别计算输入变量在前600s时刻内与输出变量互信息的最大值，以及此时所对应的时刻。

(3)在确定延迟时间后，将输入变量的时序向前调整，重构输入变量，实现与输出变量的对应。

(4)由于延迟时间可能随工况发生改变，因此当数据变化时需要对确定好的延迟时间前后一定范围内输入变量与输出变量的互信息进行计算，并从中选出最大值对延迟时间进行更新。

本文基于脱硫系统的工作原理[21]，从DCS测点上选取了与出口SO2浓度相关的八个初始输入变量，通过上述时延分析方法对筛选好的初始辅助变量进行时延分析，得到结果如表1所示。

表1 各初始输入变量时间延迟和最大互信息Tab.1 The time delay and maximum mutual information for each initial input variable

2.3 基于IMA的输入变量选择

上文通过机理分析得到了初始的输入变量，但这些变量中可能存在着部分无用变量和冗余变量。本文提出了一种基于改进蜉蝣算法(IMA)的输入变量选择方法，将变量选择与优化算法、预测模型相结合，在简化变量选择流程的同时又能够快速地寻找出与预测模型匹配的最优特征子集。基于IMA的变量选择方法流程如下：

(1)分别在各个变量前乘以0或者1的系数，并将处理后的变量用于模型预测，将预测误差作为蜉蝣算法的适应度函数；

(2)由于ELM隐含层神经元需要寻优确定，而最优神经元个数又与输入变量的数目相关，因此在上述算法中再添加一个ELM隐含层神经元个数，与各个变量前的系数共同进行寻优；

(3)通过多次迭代，蜉蝣算法最终可以找出ELM模型的最低预测误差，以及此时对应的最优特征子集、最佳隐含层神经元个数和正则化系数C。

通过上述寻优算法，最终确定模型的输入变量分别为：吸收塔PH值、入口烟气流量、入口SO2浓度、机组负荷和石灰石浆液量，ELM的最优隐含层神经元个数确定为6。

2.4 基于IMA-ELM的预测模型

将时延分析和变量选择后的数据作为最终模型的输入变量，利用ELM建立模型进行预测实验，总结算法的流程如下。

图1 实验流程图Fig.1 Experimental flowchart

3 结果与讨论

本次研究采用的模型评价指标为均方根误差RMSE和平均相对误差MAPE，其公式如下：

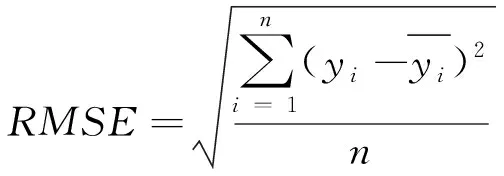
(5)

(6)

式中：yi为实际值，yi为预测值，n代表测试集样本数量。RMSE反映了总体预测值与真实值之间的误差，而MAPE则侧重反映预测值偏离真实值的程度，两者相互结合，从而对预测曲线进行合理有效的评估。

3.1 实验结果分析

本次实验采用山西某600MW燃煤电厂所提供的历史数据。通过数据清洗和预处理，最终选取了2500组代表性数据，其中前1000组作为训练集对模型进行训练，后500组作为测试集检验模型的泛化能力，数据间的采用周期为10s。

3.1.1 不同预测模型对实验结果的影响

本文在建立ELM预测模型时首先通过IMA算法对隐含层神经元个数进行优化，隐含层权值和偏差则通过随机产生。经文献[22]证明，通过对ELM隐含层权值和偏差进行优化，可以使得ELM模型的预测精度进一步提升。因此本文分别对隐含层权值和偏差优化前后的ELM进行了预测实验，最终得到的预测结果如表2所示。隐含层权值和偏差优化前后ELM的预测曲线如图2所示。

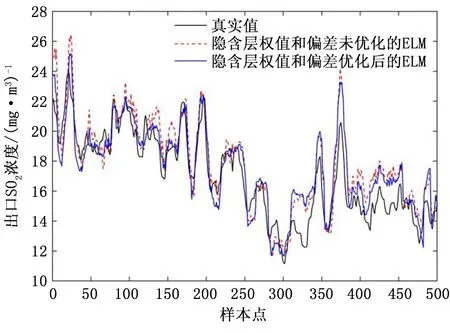
图2 不同模型预测结果图Fig.2 Plot of prediction results for different models

表2 隐含层权值和偏差优化前后ELM预测结果Tab.2 ELM prediction results before and after implicit layer weight and bias optimization

上述结果表明对于ELM的隐含层权值和偏差进行优化可以使得最终ELM的预测精度进一步提升，隐含层权值和偏差优化后的ELM其RMSE降低了12%，MAPE降低了11%。

为了进一步探究ELM在预测建模方面所具有的优势，本文选取了两种具有代表性的机器学习算法如LSSVM[23]和LSTM[24]建立对比模型。三种模型在测试集上的预测结果如表3所示。

表3 三种模型在测试集上预测结果Tab.3 Three models predict results on the test set

三种模型在测试集上的预测曲线如图3所示。

图3 三种模型在测试集上预测结果图Fig.3 Three models predict the outcome graph on the test set

从三种模型的预测结果可以看出，LSSVM的预测误差最高，模型的拟合能力最弱。LSTM具有较高的预测精度，但模型结构较为复杂，训练过程计算量极大，难以应用于实际生产中。ELM模型的预测误差最低，并且由于其特殊的前馈网络结构，ELM的训练效率较快，模型的稳定性很强。与其他两种典型机器学习建模方法相比，ELM在建立关于出口SO2浓度预测模型上具有一定的优势。

3.1.2 时延分析对实验结果的影响

为了体现改进时延分析方法对预测结果的影响，本文分别利用传统时延分析方法和改进时延分析方法对输入变量进行了时延补偿。得到的结果如表4所示。不同时延分析方法在测试集上的预测曲线如图4所示。

表4 不同时延分析方法预测结果比较Tab.4 Comparison of prediction results by different time-delay analysis methods set

3.1.3 不同优化算法对实验结果的影响

为了进一步体现改进蜉蝣算法在寻优精度上的优势，本文分别选取了原蜉蝣算法(MA)和粒子群算法[25](PSO)进行了对比预测实验：分别选取相同的训练集和测试集，设置各算法迭代次数为1000次，种群规模为30，分别对ELM模型的超参数进行优化，最终得到各ELM模型在测试集上预测结果如表5所示。不同寻优算法下ELM模型的预测结果如图5所示。

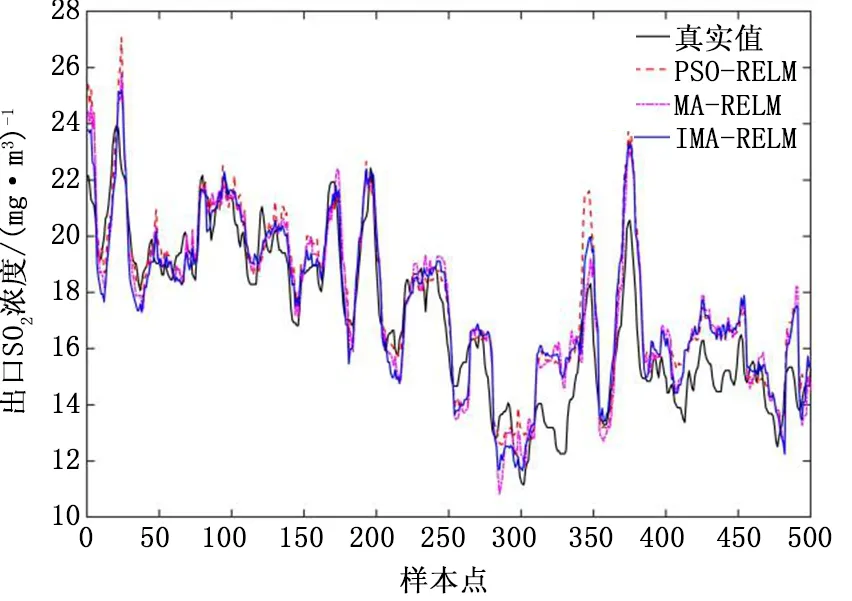
图5 不同寻优算法下ELM预测结果图Fig.5 Under different optimization algorithms ELM predicts the result graph

从表5可以看出，IMA-ELM在三种模型中的预测误差最低，MA-ELM次之，PSO-ELM最高。与PSO算法相比，MA算法由于其独特的聚集和交配行为，使得算法在收敛速度和寻优精度上都有了进一步提升。

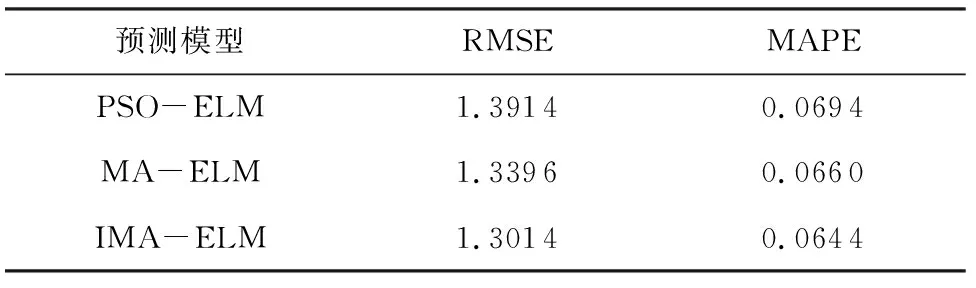
表5 不同寻优算法下ELM预测结果比较Tab.5 Comparison of ELM prediction results under different optimization algorithms

4 结论

本文针对湿法脱硫系统受机组负荷波动影响较大，难以稳定控制等问题，设计了一种基于时延分析和改进蜉蝣算法优化极限学习机的出口SO2浓度预测模型。基于IMA的变量选择方法，通过将寻优算法与变量选择相结合，从而能够快速有效的找出与ELM模型最为匹配的特征子集。利用ELM建立了相关仿真模型，实验结果表明，在对ELM隐含层权值和偏差进行优化后，模型的均方根误差从1.4775下降到1.3014，模型误差下降了12%；利用互信息算法对输入变量进行时延分析并补偿，模型精度提升了5%；利用IMA算法对模型参数进行优化，相比于PSO、MA优化后的模型，IMA-ELM模型的预测误差分别下降了0.0914和0.0396。基于实际运行数据的仿真实验表明，IMA-ELM预测模型可以对出口SO2浓度变化趋势进行准确预测，进而为运行人员控制脱硫系统平稳运行提供参考，对于提高脱硫效率和节约脱硫成本具有重要意义[26]。