扣接封闭箍筋约束浆锚连接剪力墙抗震性能*

汤 磊 周恩泉

(东南大学土木工程学院，南京 210096)

0 引 言

装配式混凝土剪力墙结构是我国装配式建筑采用的重要结构形式，预制剪力墙的连接节点力学性能决定了结构抗侧力性能，是结构抗震关键节点。大量学者针对综合无黏结预应力连接和普通钢筋连接的混合连接剪力墙的抗震性能及耗能能力进行了研究[1-6]；Li等提出了钢筋骨架支撑剪力墙，并取消了分布区钢筋的连接[7]；Chu等提出了预制模壳剪力墙，钢筋在模壳空腔内搭接连续[8]；Menegon等研究了采用角部钢板焊接连接的电梯井筒结构的抗震性能[9]；Zhou等提出了内埋双层钢管混凝土连接技术[10]；Shen等将后焊钢板剪切连接键用于预制剪力墙竖向拼缝以减小拼缝两侧墙体相对变形[11-12]；文献[13]将组合结构概念引入剪力墙配筋方案中[13]。

我国当前推行“等同现浇”理念，钢筋套筒灌浆连接[14]、钢筋浆锚搭接连接[15]及后浇混凝土连接[16]受到普遍关注。其中，对于钢筋浆锚搭接连接技术，钢筋搭接传力可靠性长期受到质疑，因此，在剪力墙边缘构件引入课题组前期提出的扣接封闭箍筋技术，以增强对波纹管浆锚搭接接头及混凝土的约束性能，形成扣接封闭箍筋约束波纹管浆锚连接技术，构造示意见图1。

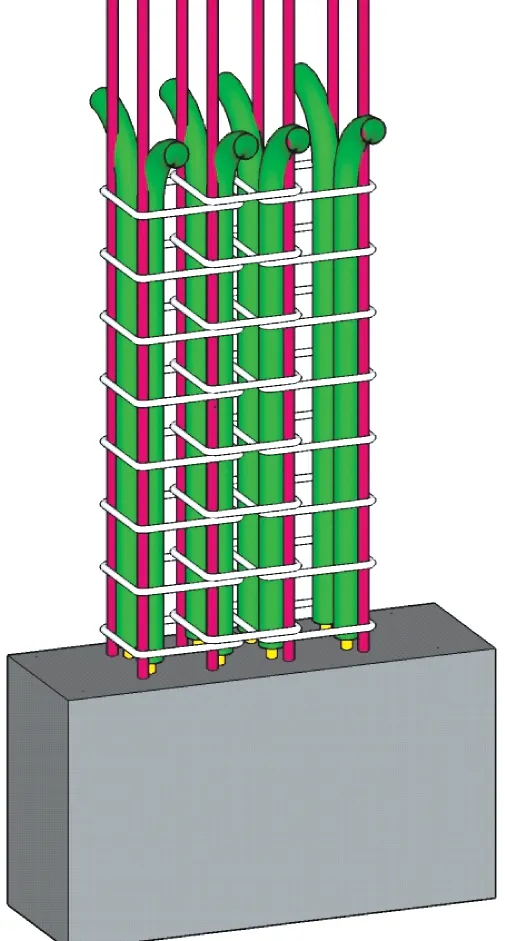
图1 扣接封闭箍筋约束波纹管浆锚示意Fig.1 The schematic diagram of grouted bellows constrained by overlapped closed stirrups

为探讨扣接封闭箍筋约束波纹管浆锚连接剪力墙抗震性能，对1个装配式剪力墙试件和1个对比用现浇剪力墙试件进行低周反复荷载试验。基于试验结果，采用MATLAB软件对约束波纹管浆锚连接剪力墙试件开展参数分析，以掌握各关键参数对其力学性能的影响规律，为设计提供建议。

1 试验过程

1.1 试件设计与加工

共制作2个同尺寸试件：1个为装配式试件，采用扣接封闭箍筋约束波纹管浆锚连接技术；1个为现浇对比试件，编号分别为PW、MW。试件由底座、剪力墙和加载梁三部分组成，剪力墙截面尺寸见图2a，试件MW、PW截面配筋分别见图2b、图2c。

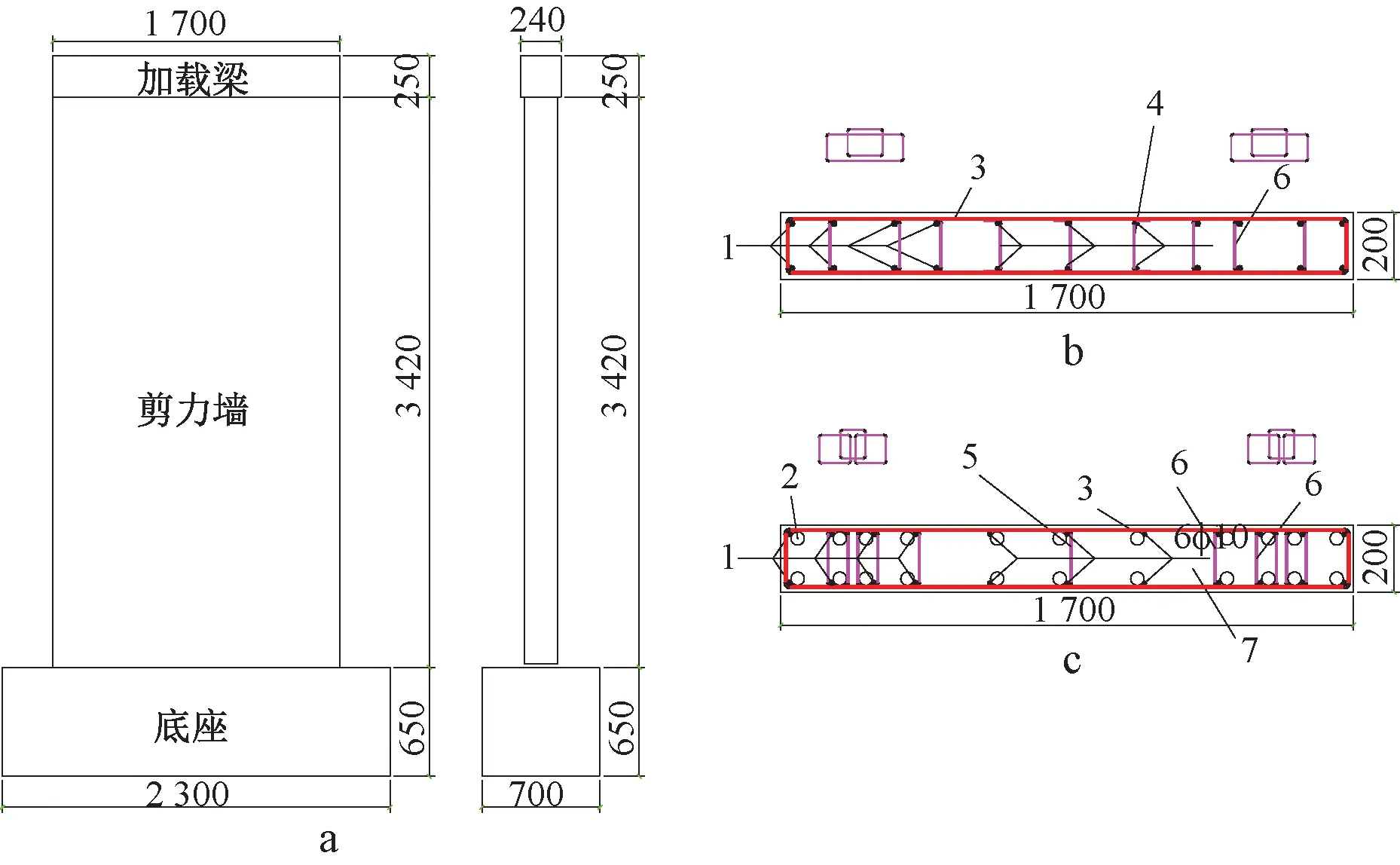
a—试件尺寸；b—MW截面详图；c—PW截面详图。1—8φ16纵筋；2—φ40金属波纹管；3—φ10@200水平钢筋；4—φ5@600拉筋，交错布置；5—φ8@600拉筋，交错布置；6—φ8@100箍筋；7—6φ10纵筋。图2 试件设计 mmFig.2 Design drawings of specimens

试件采用C35混凝土制作，所有钢筋强度等级均为HRB400，采用φ40金属波纹管，灌浆料型号为BY(S)-40。竖向钢筋浆锚长度均设置为600 mm，并采用闪光对焊形成焊接封闭箍筋。

1.2 材料性能

试件制作用混凝土实测立方体抗压强度为35.4 MPa，换算得混凝土轴心抗压强度为23.7 MPa，灌浆料实测抗压强度为74.8 MPa，所用钢筋材料性能见表1。

表1 钢筋材性数据Table 1 Material properties of rebars

1.3 试件加载与测试

试件加载装置示意见图3。试件通过8根地脚螺杆固定在实验室地面上；试件竖向荷载通过2束、8根体外预应力钢绞线施加；试件水平荷载通过1 000 kN电液伺服作动器(MTS)施加。

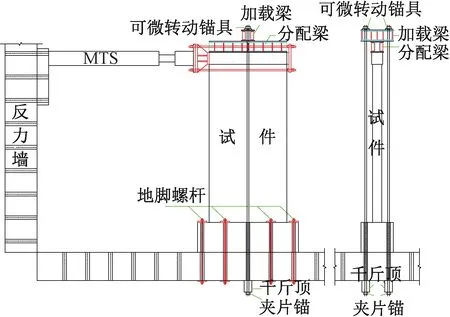
图3 试验加载装置Fig.3 Test setup

试验采用恒定轴压下的低周反复水平荷载加载方法，先施加轴压并保持恒定，试验轴压比为0.10，需施加轴力为805 kN。后施加水平反复荷载，并采用力和位移双控制度，即屈服前按力控制加载，每级循环1次，屈服后按屈服位移控制加载，每级循环3次，直至试件承载力下降到极限承载力的85%以下或不适宜继续加载则试验终止。加载过程中，规定作动器外推为正，内拉为负。

2 试验结果及分析

2.1 破坏形态对比

2个试件破坏过程相同，最终均由受拉钢筋拉断、受压混凝土压溃而导致承载力降低而破坏，其破坏形态见图4。从图中可以看出，两者均呈现弯剪破坏状态，裂缝分布形态基本相似。由于扣接封闭箍筋的有力约束，试件PW角部受压混凝土压溃高度明显小于试件MW。

2.2 滞回曲线与骨架曲线

试件滞回曲线与骨架曲线见图5。可以看出，两者滞回曲线形状均较为饱满，表现出良好的滞回性能；两者骨架曲线走势基本一致，初始弹性阶段两者曲线基本重合，在弹塑性阶段具有稳定的承载力，且由于试件PW坐浆层灌浆料具有较混凝土更高的强度，弹塑性阶段其表现出较试件MW更高的承载力。

a—MW；b—PW。图4 试件破坏形态Fig.4 Failure modes of specimens

a—试件MW滞回曲线；b—试件PW滞回曲线；c—骨架曲线。图5 试件滞回曲线及骨架曲线Fig.5 Hysteretic curves and skeleton curves of specimens

2.3 承载能力与变形能力

各试件在开裂、屈服、峰值和极限阶段的承载力及变形数据见表2。从数据对比可以看出，试件PW具有与试件MW相当的承载力与变形能力，由于灌浆料较混凝土具有更高强度且钢筋浆锚连接段钢筋面积较大，使得试件PW峰值荷载更高，而灌浆料的脆性特性造成其极限阶段荷载下降较多。

表2 试件承载力与变形数据Table 2 Bearing capacity and deformation of specimens

同时，由表2可以看出，2个试件承载力试验值均高于设计值，而试件PW具有更高的安全储备。

2.4 刚度退化

采用割线刚度表征试件刚度，其计算参见文献[17]，试件在加载过程中的刚度退化情况见图6。可以看出，两者刚度退化发展规律基本相同，同时由于扣接封闭箍筋约束有效延缓了混凝土的失效，试件PW表现出更好的刚度特性。

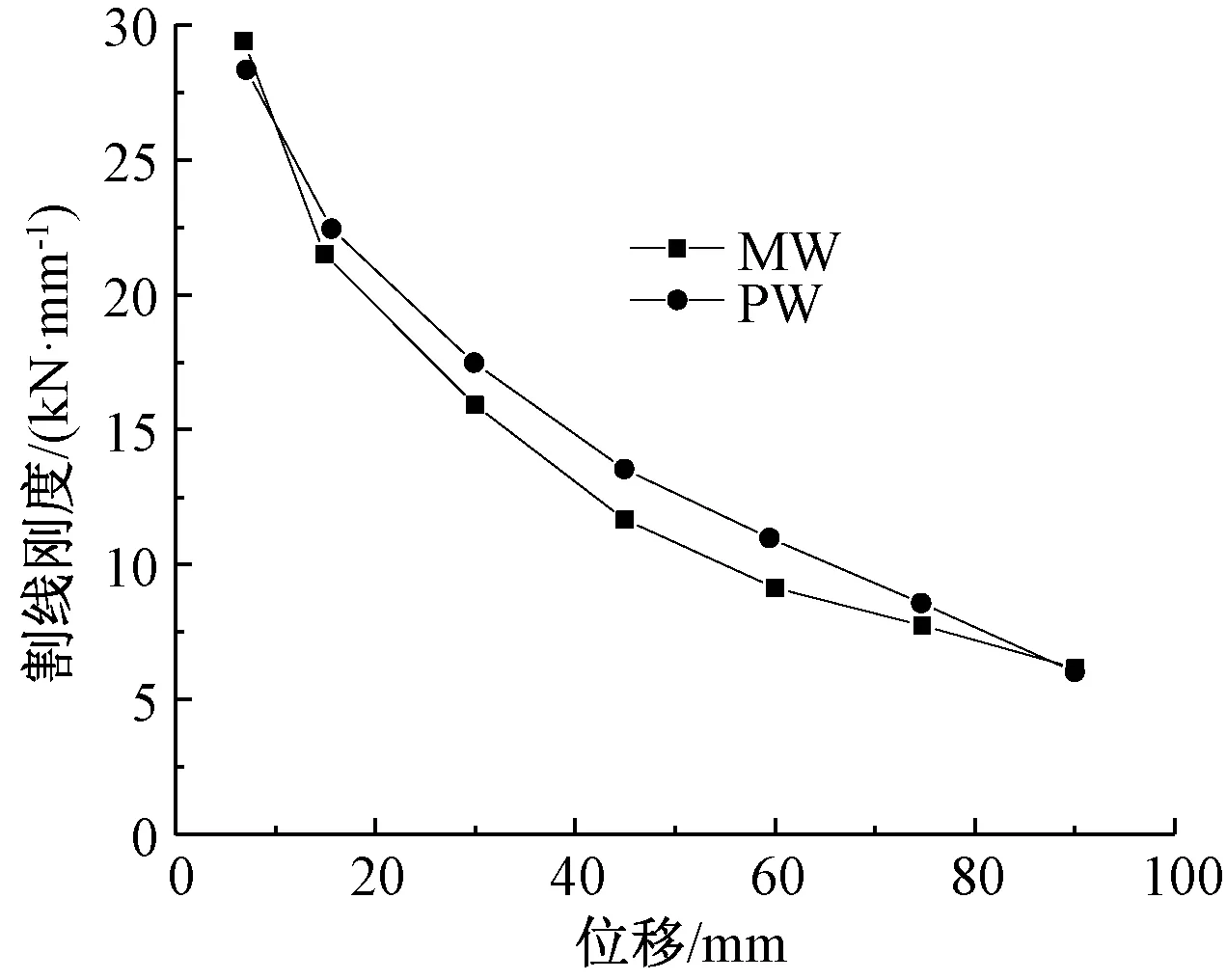
图6 刚度退化曲线Fig.6 Stiffness degradation curves

2.5 位移延性性能

基于骨架曲线，采用Park法[18]确定试件屈服位移，再计算位移延性系数，计算结果见表3。在变形能力相当的前提下，试件PW位移延性系数较试件MW有一定程度降低，分析认为主要是由于水平拼缝引起的变形集中及灌浆料的脆性特性引起。

表3 试件位移延性系数Table 3 Displacement ductility coefficients of specimens

2.6 耗能能力

采用等效黏滞阻尼比衡量试件耗能能力，其计算参见文献[17]，试件在加载过程中的等效黏滞阻尼比变化情况见图7。可以看出，试件PW表现出与试件MW接近的耗能能力。

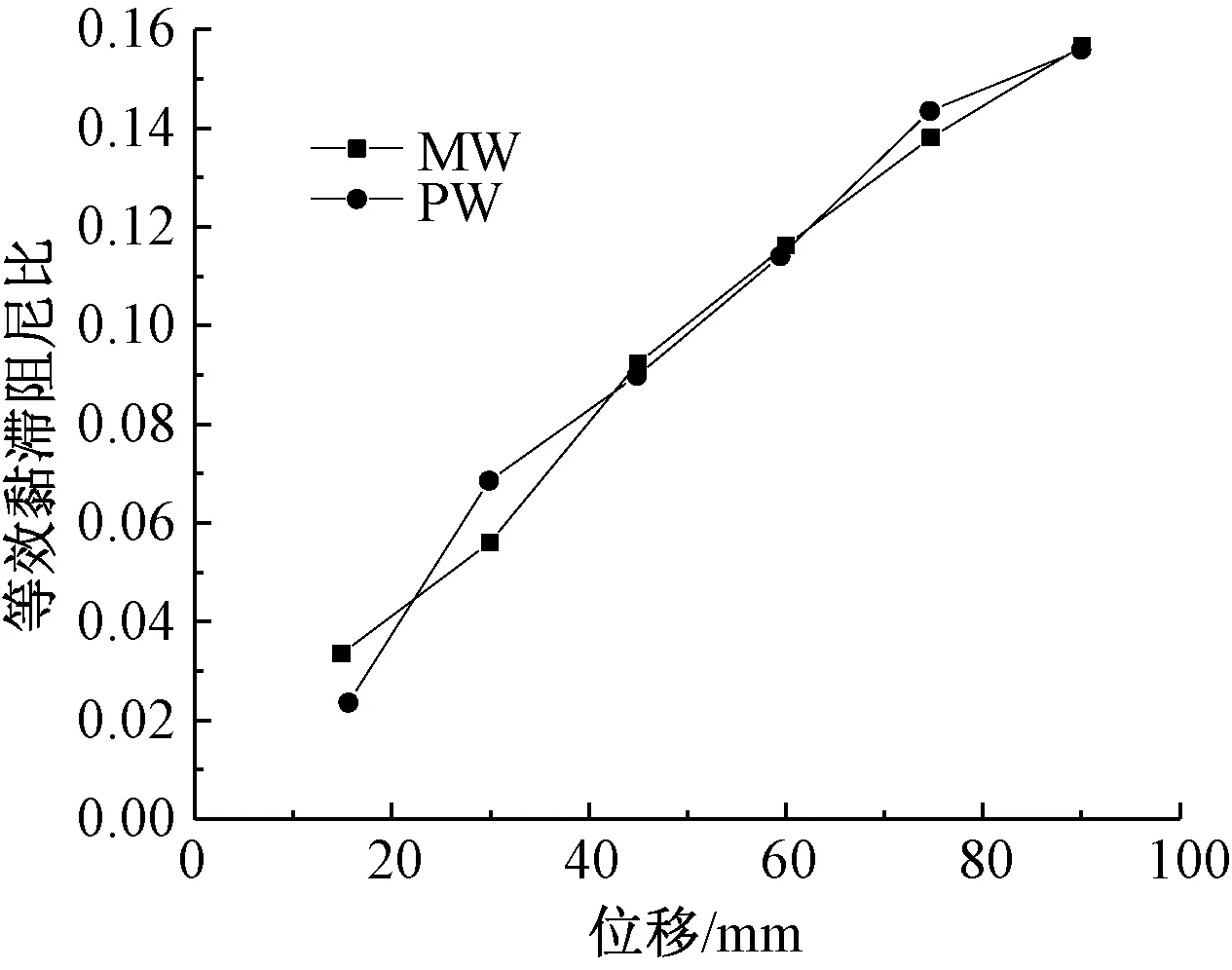
图7 试件等效黏滞阻尼系数Fig.7 Equivalent viscous coefficients of specimens

3 MATLAB参数分析

基于MATLAB平台，编制扣接封闭箍筋约束波纹管浆锚连接剪力墙在水平单调荷载作用下的荷载-位移关系的计算程序，在与试验结果验证的基础上，进一步开展考虑轴压比、剪跨比、边缘构件长度、竖向钢筋配筋率、边缘构件配箍特征值及混凝土强度等参数分析，以进一步掌握其力学性能。

3.1 分析程序概况

3.1.1基本假设

1)鉴于等同现浇设计理念，装配式剪力墙截面分析时，仍然遵循平截面假定。

2)在单调水平荷载作用下，剪力墙仅发生平面内侧向变形，且装配式剪力墙水平拼缝处不会发生剪切滑移。

3)为简化分析程序，截面上灌浆料部分用混凝土母材代替，认为是偏于安全的。

3.1.2材料本构模型

1)混凝土。

进行截面分析时，将截面上混凝土按照约束情况为三种：保护层混凝土、边缘构件约束混凝土、中部分布区混凝土。

为更好地区分不同约束条件下混凝土受压性能的变化，并进一步逼近试验效果，经过分析及试算，最终采用Hognestad模型[19]模拟保护层混凝土和中部分布区混凝土受压性能，采用Mander模型[20]模拟边缘构件约束构件混凝土受压性能。

同时，为体现装配式剪力墙与现浇剪力墙的区别，对于水平拼缝截面分析时，装配式剪力墙中混凝土不考虑其抗拉性能，而现浇剪力墙则考虑其抗拉性能，混凝土受拉性能采用我国GB 50010—2010《混凝土结构设计规范》附录C建议的本构模型。

2)钢筋。

偏于安全且简便计算，采用二折线模型模拟钢筋本构，且不考虑钢筋材料硬化。

3.1.3分析程序

本次MATLAB分析分为截面弯矩-曲率分析及试件荷载-位移曲线计算两个流程。

1)截面弯矩-曲率分析。

对于截面弯矩-曲率关系计算，采用条带法分析。具体过程见图8。

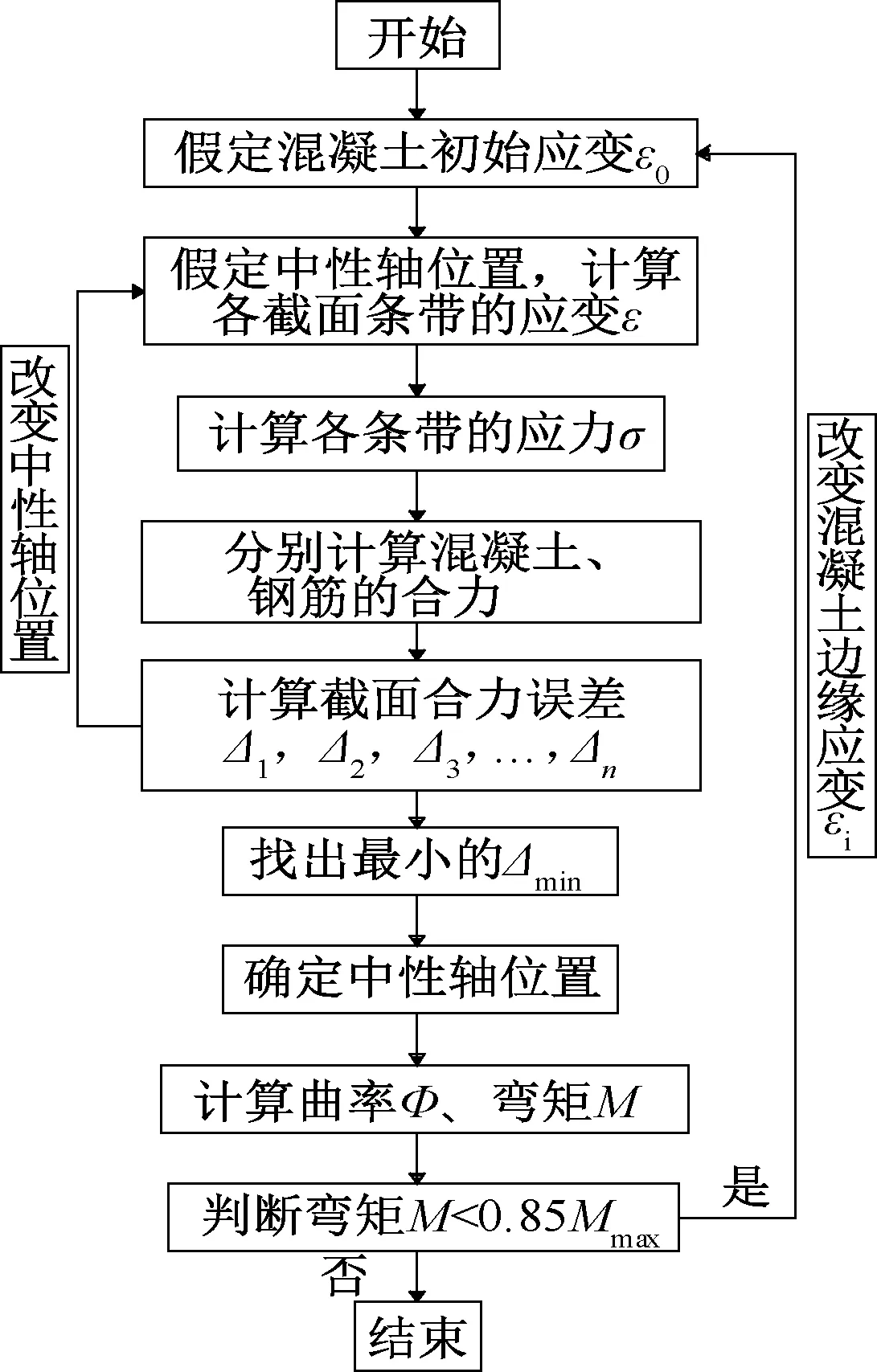
图8 截面弯矩-曲率计算流程Fig.8 Calculation process for relations between sectional moment and curvature

2)试件荷载-位移曲线计算。

对于试件荷载-位移曲线计算，根据各等级荷载下试件内力分布，基于截面弯矩-曲率关系，采用逐段积分求和法计算试件位移。具体计算过程见图9。

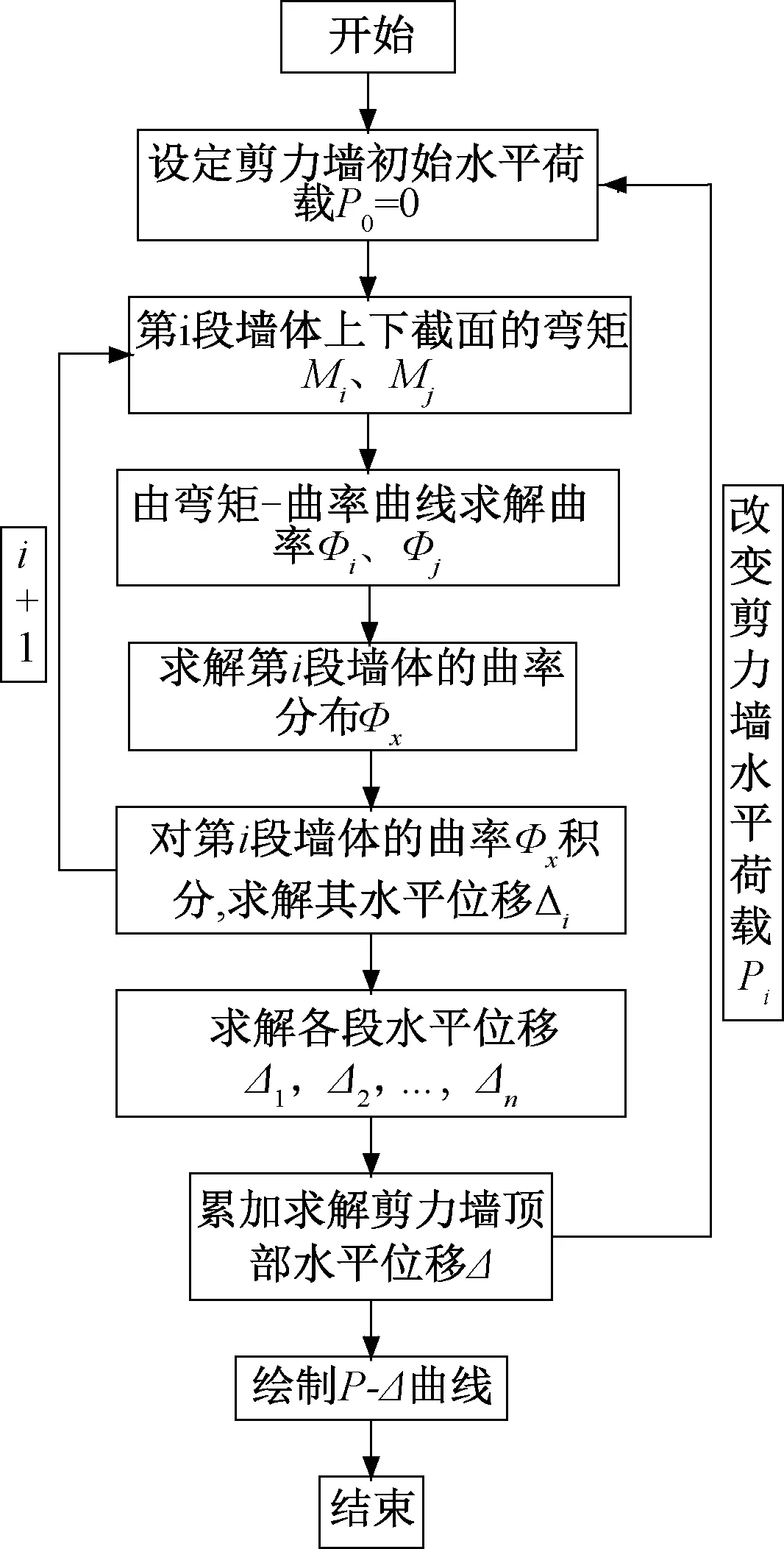
图9 试件荷载-位移计算流程Fig.9 Calculation process for relations between load and displacement

3.2 程序验证

将MATLAB程序计算单调荷载-位移曲线与试验实测正向骨架曲线对比，见图10。

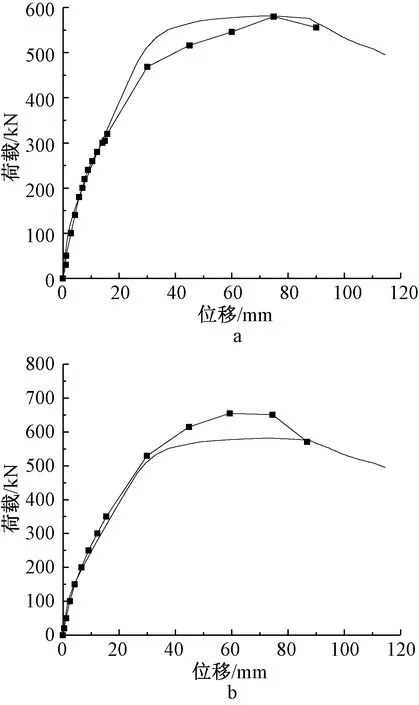
a—MW；b—PW。—实测；——MATLAB。图10 分析与实测曲线对比Fig.10 Comparisons of analysis results and test data

从图中可以看出，MATLAB分析结果能较好地反映试验曲线，初始弹性阶段能很好地吻合；弹塑性阶段由于未考虑钢筋材料硬化特性及钢筋混凝土界面滑移等因素，试件MW的MATLAB曲线稍高于实测曲线，而由于未考虑灌浆料高强度、脆性的特性，试件PW的MATLAB曲线则低于实测曲线。

另外，计算过程中发现，考虑混凝土受拉性能对试件整体性能曲线影响不大，从侧面说明对于装配式剪力墙，只要通过合理构造保证钢筋连续受力、确保混凝土受压性能，可实现等同现浇。

3.3 参数分析

参数分析中的基准试件参数直接采用本次试验试件设计，仅其轴压比由0.10变为0.20。

3.3.1轴压比参数分析

在其他条件保持不变的条件下，计算轴压比参数取值为0、0.10、0.15、0.20、0.25、0.30、0.35、0.40及0.50情况下试件的力学性能参数，见图11。可以看出，当轴压比不大于0.40时，试件承载力随轴压比增大而提高，但提高幅度逐渐降低；当轴压比大于0.40时，试件承载力反而降低；随轴压比增大，试件变形能力逐渐降低。分析认为，在轴压比较低的情况下，轴压比增大、竖向压力增大，进一步抵消由水平荷载产生的倾覆弯矩，但轴压比过大，使得受压混凝土初始压应变过高，随着水平荷载逐渐增大，受压混凝土会提前到达极限状态，从而影响试件整体承载力及变形能力的发挥。综合承载力与变形能力要求，建议设计轴压比不超过0.4。

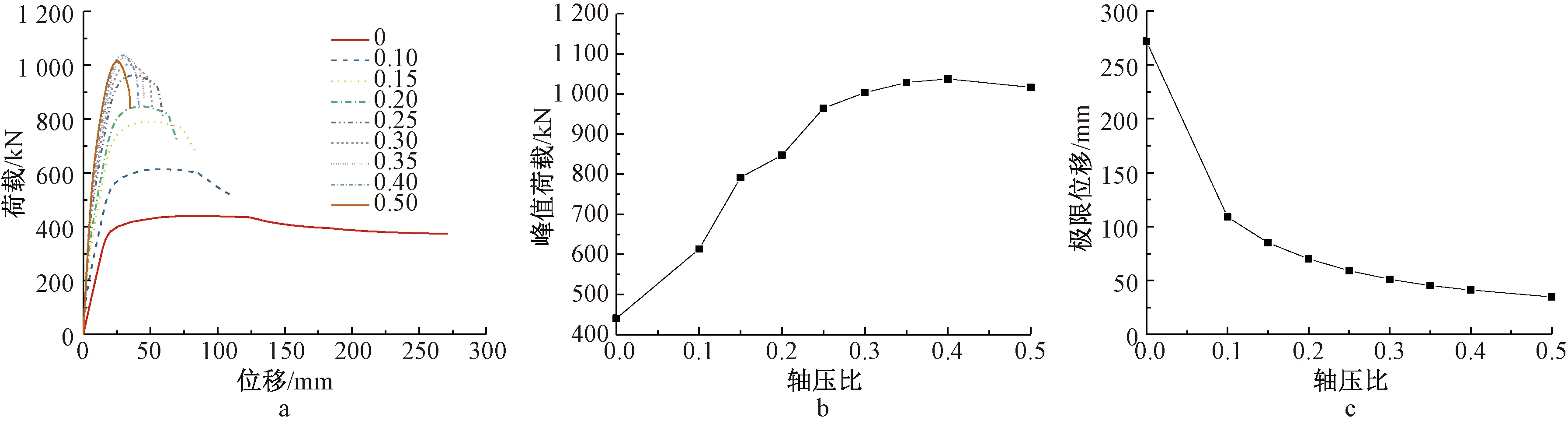
a—荷载-位移曲线；b—轴压比-峰值荷载曲线；c—轴压比-极限位移曲线。图11 轴压比参数分析结果Fig.11 Results of parameter analysis of axial compression ratios

3.3.2剪跨比参数分析

在其他条件保持不变的条件下，通过改变剪力墙高度来模拟剪跨比的变化。

剪跨比为1.0、1.5、2.0、2.5、3.0及3.5情况下的试件计算结果见图12。可以看出，随着剪跨比增大，试件承载力降低、变形能力提高，且其对试件变形能力影响更为显著，剪跨比从1.0增大至3.5，试件承载力降低约71%、极限变形提高约12倍。同时，从图12a、b中可以看出，剪跨比至2.5以后，承载力降速明显减缓。另外，考虑到剪跨比越大，试件越趋向于弯曲破坏，利于抗震，因此，建议设计时剪跨比不宜低于2.5。

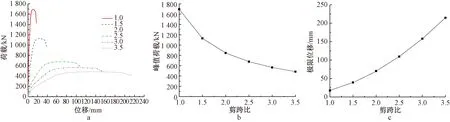
a—荷载-位移曲线；b—剪跨比-峰值荷载曲线；c—剪跨比-极限位移曲线。图12 剪跨比参数分析结果Fig.12 Results of parameter analysis of shear-span ratios

3.3.3边缘构件长度参数分析

在其他条件保持不变的条件下，改变剪力墙边缘构件长度，同时通过修改边缘构件竖向钢筋面积来保证竖向钢筋配筋率不变。

边缘构件长度为200 mm(≈0.12hw，hw为剪力墙截面高度1 700 mm)、300 mm(≈0.18hw)、400 mm(≈0.24hw)、500 mm(≈0.29hw)、600 mm(≈0.35hw)和700 mm(≈0.41hw)情况试件计算结果见图13。可以看出，随着边缘构件长度增大，试件承载力逐渐提高，而变形能力先升后降，并在400 mm(≈0.24hw)处达到峰值。鉴于此处400 mm边缘构件长度为试验试件设计时参照GB 50011—2010《建筑抗震设计规范》(2016版)确定的数值，因此，综合承载力及变形能力要求，建议设计中按照GB 50011—2010要求确定合理的边缘构件长度。

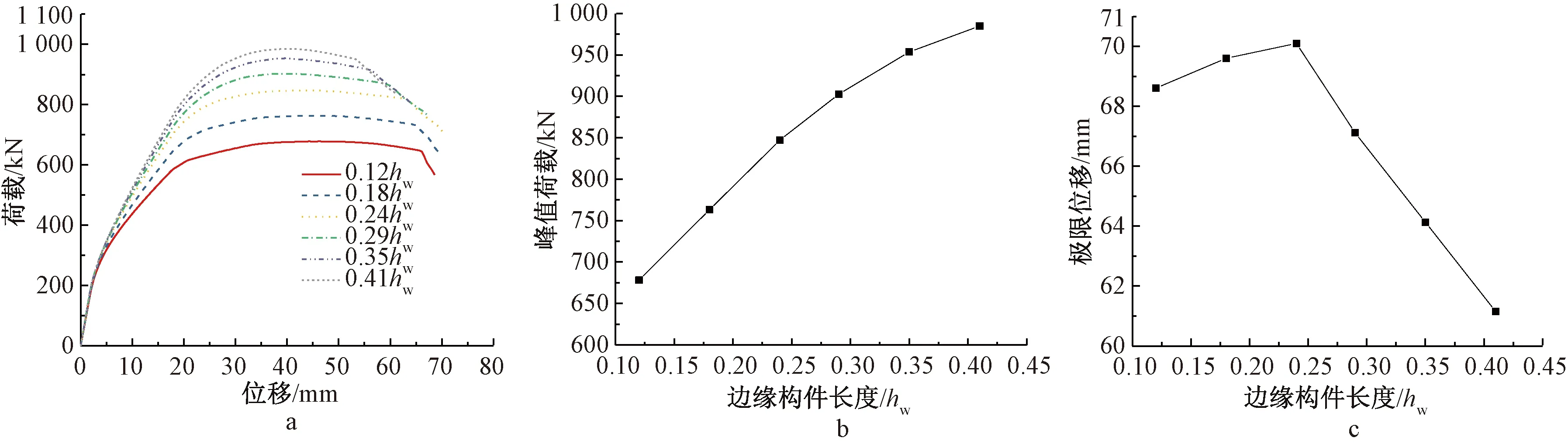
a—荷载-位移曲线；b—边缘构件长度-峰值荷载曲线；c—边缘构件长度-极限位移曲线。图13 边缘构件长度参数分析结果Fig.13 Results of parameter analysis of boundary element lengths

3.3.4竖向钢筋配筋率参数分析

在其他条件保持不变的条件下，通过改变边缘构件钢筋直径、不改变钢筋位置，来模拟边缘构件竖向钢筋配筋率变化。

3.3.5边缘构件配箍特征值参数分析

在其他条件保持不变的条件下，通过改变箍筋间距、保持箍筋直径及肢数不变来模拟边缘构件配箍特征值变化。

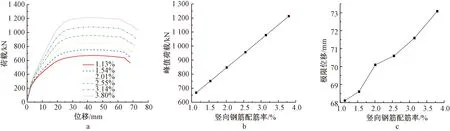
a—荷载-位移曲线；b—竖向钢筋配筋率-峰值荷载曲线；c—竖向钢筋配筋率-极限位移曲线。图14 竖向钢筋配筋率参数分析结果Fig.14 Results of parameter analysis of vertical reinforcement ratios of boundary elements

边缘构件配箍特征值为0.14(@250 mm)、0.18(@200 mm)、0.24(@150 mm)、0.36(@100 mm)、0.52(@70 mm)和0.72(@50 mm)情况下的试件计算结果见图15。可以看出，边缘构件配箍特征值对试件弹性阶段受力性能基本无影响，而对弹塑性阶段受力性能有一定影响，且随着配箍特征值增大，试件承载力一定程度提高、变形能力则显著提高，说明边缘构件配箍特征值的增大明显有利于试件延性及变形能力的提高。

a—荷载-位移曲线；b—边缘构件配箍特征值-峰值荷载曲线；c—边缘构件配箍特征值-极限位移曲线。图15 边缘构件配箍特征值参数分析结果Fig.15 Results of parameter analysis of stirrup characteristic values of boundary elements

3.3.6混凝土强度参数分析

在其他条件保持不变的条件下，计算混凝土强度等级为C30、C35、C40、C50和C60情况下的试件力学性能参数，见图16。可以看出，随着混凝土强度等级的提高，试件承载力及变形能力均得到提高，但提高幅度不大，从C30提高至C60，试件承载力提高约14%、极限位移提高约17%，说明混凝土强度等级在满足设计最低要求的条件下，对试件力学性能影响不甚明显。

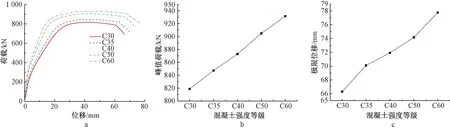
a—荷载-位移曲线；b—混凝土强度-峰值荷载曲线；c—混凝土强度-极限位移曲线。图16 混凝土强度参数分析结果Fig.16 Results of parameter analysis of concrete strengths

4 结束语

为验证采用扣接封闭箍筋代替传统箍筋约束波纹管浆锚连接剪力墙的抗震能力，对1个现浇对比试件(MW)与1个扣接封闭箍筋约束浆锚连接剪力墙试件(PW)开展了低周反复荷载试验。并基于试验结果，采用MATLAB编制分析程序进行了参数分析。

根据试验及参数分析结果，得出以下主要结论：

1)通过综合对比2个试件的破坏形态、承载力、变形能力、刚度退化、位移延性及耗能能力等试验关键指标，试件PW具有良好的抗震能力，实现了等同现浇的设计目标。

2)参数分析结果表明：试件承载力随着轴压比增大先升后降、随边缘构件长度增大而提高、随竖向钢筋配筋率增大而提高、随边缘构件配箍特征值增大而无明显变化、随混凝土强度提高有一定程度增大；试件变形能力随着轴压比增大而降低、随边缘构件长度增大先升后降、随竖向钢筋配筋率增大而无明显变化、随边缘构件配箍特征值增大而明显提高、随混凝土强度提高有一定程度增大。

3)结合试验与参数分析结果，综合承载力及变形能力要求，对波纹管浆锚连接剪力墙构件的设计提出以下建议：轴压比宜控制在0.4以下；剪跨比不宜小于2.5；边缘构件长度可按照现行现浇混凝土相关规范要求设置；设计允许且施工可行时，宜尽量提高边缘构件配箍特征值；混凝土强度满足设计要求即可。