不锈钢芯板T形墙双向压弯性能研究

2022-09-01舒兴平黄鑫源王元清

工业建筑 2022年6期

舒兴平黄鑫源王元清

(1.湖南大学土木工程学院钢结构研究所，长沙 410082；2.清华大学土木水利学院，北京 100084)

不锈钢开始应用于建筑行业已经有半个多世纪了，但目前大都只是用于屋面装饰以及围护设施等非承重体系。它与普通低碳钢一样，材质均匀，构件截面面积小、容重小；较之普通钢材，其耐腐蚀性、可回收利用性又尤为突出。

蜂窝夹芯板结构最初是用来制作早期的夹层结构机翼，后来又研发出了金属类和玻璃纤维增强蜂窝夹芯材料；而早期夹芯板只用于航空航天器等对轻量化、可靠性要求极为苛刻的领域，随着夹芯板材料品种的不断丰富，制造成本的不断下降，开始广泛用于其他领域[1]。

为了适应越来越高的建筑设计和布局要求，在建筑物中布置异形墙体或异形柱是通用的做法，如T、L形墙、H形截面墙等。这一类异型构件相比起常见的只能承受面内弯矩、剪力的一字形构件的优势就在于其在面内外都有一定的承载力和刚度，因此可以承受双向弯曲和剪切。黄真锋等对4个T形多腔钢-混凝土组合构件的压弯性能进行了试验研究和有限元参数分析，得出了截面高厚比是影响压弯承载力相关曲线的最关键参数[2]；Wang等对混凝土双壁钢波纹板T形组合墙在轴向压缩和双向弯曲的共同作用下的承载能力进行了研究，通过大量有限元分析得出了不同轴压比下Mx-My的相互作用方程[3]。

不锈钢芯板结构是湖南长沙远大科技集团发明与湖南大学合作研发的一种新型夹芯板结构形式。通过将不锈钢蒙皮面板和圆筒芯管在专业设备中以热风铜钎焊的方式连接起来，共同承受荷载，且不锈钢芯板在厂房内按照一定的模数生产完毕后，经过切割、焊接等工序，形成墙、梁、板等大型承重构配件。近年来，已有一些对该类结构的研究，蔡华根等通过对2块足尺不锈钢芯板四边简支楼板构件的试验研究和有限元分析，得出该种结构作为楼板设计时计算中主要应控制挠度[4]。闫肃等通过对6面不锈钢芯板T形墙的轴压试验和有限元分析，得出T形墙受到轴压时，局部鼓曲是主要破坏形态[5]。且随着面板厚度增加，芯管对承载力贡献越来越小。舒兴平等通过对4面面板厚度不同的不锈钢芯板一字形墙进行拟静力试验以及大量的参数分析，得出不锈钢芯板一字型剪力墙具有良好的延性和耗能能力[6]。本文主要通过ABAQUS软件对不锈钢芯板T形墙在承受双向压弯荷载作用下的受力性能和破坏过程进行研究，通过大量的有限元模型计算，对可能影响其压弯承载力的多种因素进行分析，最终得出N、Mx、My的数值关系。

1 不锈钢材性

与常用的低碳钢不同，不锈钢属于典型的非线性材料，其本构关系曲线较平滑，无明显的屈服点和屈服平台，比例极限较低，一般取塑性应变为0.2%时对应的应力作为名义屈服点σ0.2，并且当前建筑工程常用的S304级奥氏体不锈钢的名义屈服点大都要略低于低碳钢，但是比起低碳钢又有更长的应变强化段[7]。二者本构关系对比大致如图1所示。

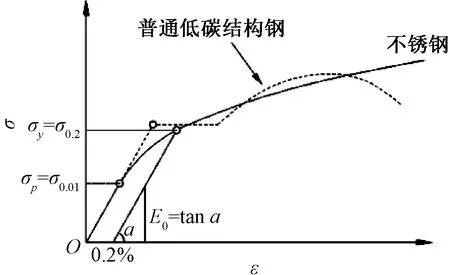
图1 建筑用不锈钢和低碳钢本构曲线对比Fig.1 Comparisons of constitutive curves of stainless steel and low-carbon steel for buildings

当采用名义屈服点较低的不锈钢材料(如奥氏体S304、S316不锈钢)时，本构非线性对结构承载力影响较大，必须充分考虑应变硬化段的影响[8]。本文中所采用的奥氏体S304L不锈钢含碳量远低于常见的S30408不锈钢，其由焊接引起的晶体间腐蚀敏感性较低，故而更加适合用作大型焊接构件类用材[9]，但相应的屈服强度也要低于S30408不锈钢，目前对该种不锈钢的材性研究一般仅限于拉伸状态，考虑到本文中构件模型在双向压弯状态下，截面以受压为主，故依据GB/T 32498—2016《金属基复合材料拉伸试验室温试验方法》[10]和GB/T 7314—2017《金属材料室温压缩试验方法》[11]设计了若干拉伸与压缩试件[12]，试验情况如图2所示，试验结果见表1、表2。

图2 材性试验仪器及部分试件Fig.2 Material property testing equipment and specimens

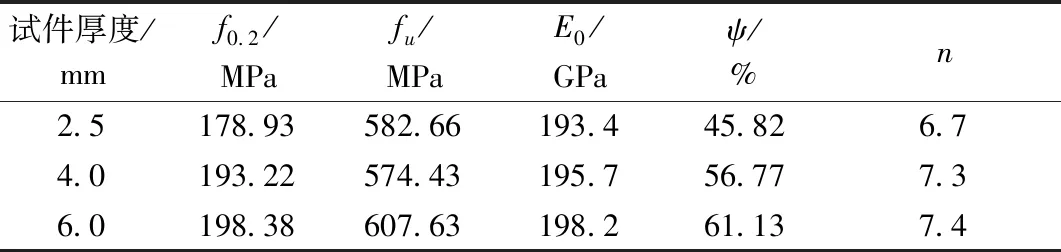
表1 S304L材性试件拉伸试验数据Table 1 Tensile test data of S304L specimens

表2 S304L材性试件压缩试验数据Table 2 Compression test data of S304L specimens

经材性试验后，各种厚度试件的受拉屈服强度与CECS 410∶2015《不锈钢结构技术规程》[13]S30403不锈钢规定的抗拉强度标准值相比非常接近，且同厚度试件受压缩时初始弹性模量E0和屈服强度要略低于受拉伸时状态，故本文数值分析模型中材性参数均采用压缩试验得出的结果。

2 有限元分析

2.1 建立模型

采用有限元分析软件ABAQUS建立了9组数值分析模型来研究不锈钢芯板T形墙的双向压弯力学性能，由于芯板结构的板壁和芯管壁厚远小于其他方向尺寸，所以在建模时均采用ABAQUS软件单元库中的S4R单元(四结点四边形减缩积分壳单元)。

通过合并命令将各部件组装成一个整体后(图3)，在上下底面分别设置参考点，并将上下底面分别耦合于上下参考点上，限制下参考点所有方向的线位移和绕z轴方向的转动自由度，限制上参考点x、y方向的线位移和绕z轴的旋转，先按照设定轴压比下的轴力加载于上参考点，轴力加载完毕后，再通过在两个加载点上施加大小相同、矢量方向相反的角位移，完成对构件压弯荷载的施加，边界条件和载荷具体设定详见图4。

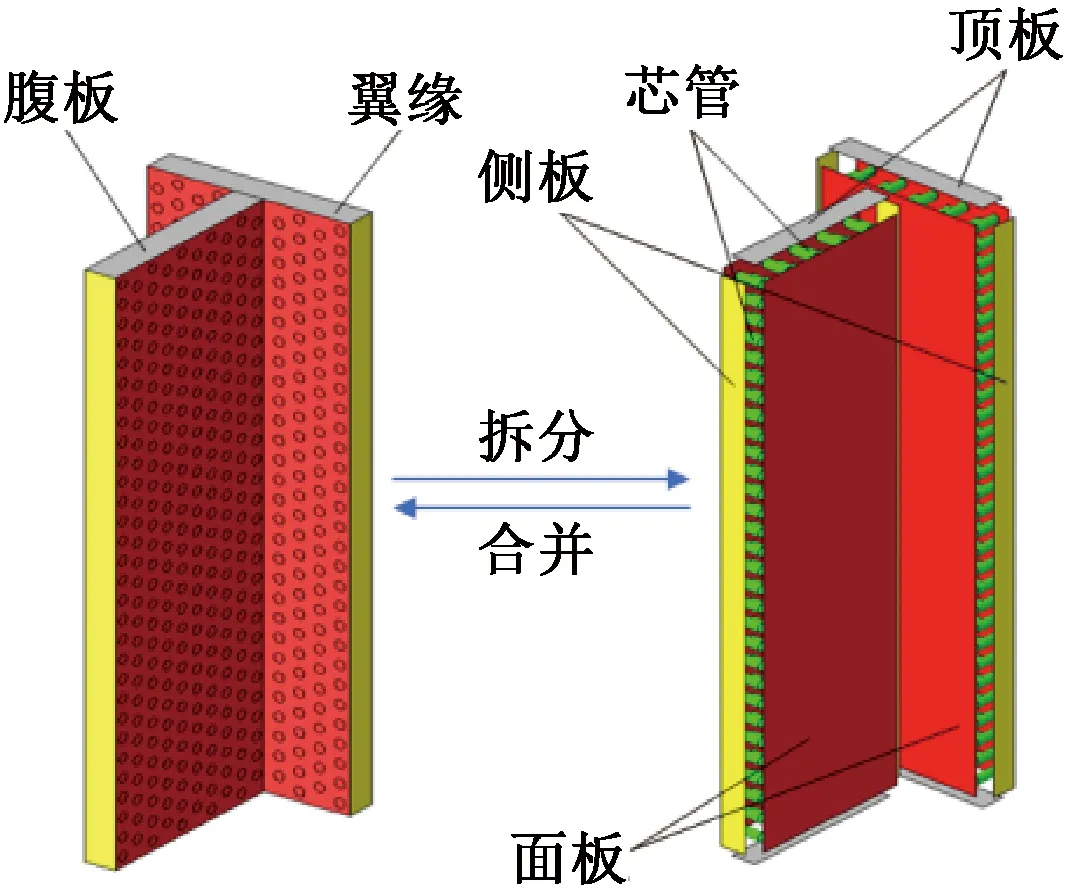
图3 不锈钢芯板T形墙组合分解模型Fig.3 The decomposition model diagram of T-shaped wall with stainless steel core plate

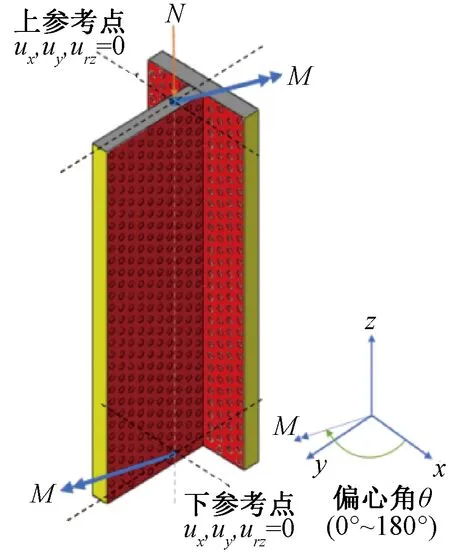
图4 边界条件和载荷示意Fig.4 The schematic diagram of boundary conditions and loads

由于薄壁钢结构的几何初始缺陷对受压承载力有不可忽略的影响，因此在分析过程中需要引入几何初始缺陷。即将经过屈曲分析得出的新节点坐标文件替换原有模型的节点坐标，并控制幅值为l/1 000(l为墙高)，从而将板件的初始局部鼓曲和整体初弯曲的影响考虑在内，最后对原模型进行非线性结构分析。

2.2 破坏形态

本文总共建立了12组不锈钢芯板T形墙数值分析模型，对应规格、加载变量及最终极限承载力详见表3(其中面板6 mm厚的TQYW-6.0-1～3为标准构件)。

表3 模型构件分组及规格Table 3 Grouping and specifications of model components

12组模型最终的破坏情况，主要是以面板、侧板的局部屈曲为主，但当面板厚度超过6 mm，轴压比较小时，在承载力达到极限之前，已经有较为明显的整体弯曲。本文以试件TQYW-6.0-2为例，介绍T形墙的压弯破坏全过程，其弯矩-转角曲线(M-φ)如图5所示。

图5 TQYW-6.0-2弯矩-转角曲线Fig.5 The bending moment-rotation curve of TQYW-6.0-2

Ⅰ阶段(弹性受力)：构件模型的荷载-转角曲线近似成线性关系，构件中所有部件应力均未达到比例极限，此时T形墙受压侧墙肢均为受压，较大压应力大多分布于试件两墙肢受压区面板近加载端处以及面板和侧板交界处，主要是由于轴力和弯矩的叠加使得此处压应力最大，以及交界尖角处有局部应力集中现象引起的，详见图6。受压区除加载端附近应力集中外，其他均匀受压，受拉或受压均未达到材料屈服强度，构件处于弹性状态。芯管在应力最大处应力不超过40 MPa，说明在弹性阶段芯管所起支承作用较小；随着施加转角的增大，直到M-φ曲线开始出现明显斜率变化，即到达拐点，此时面板侧板最大纵向压应力达到约180 MPa，构件开始进入弹塑性阶段。

图6 TQYW-6.0-2第Ⅰ阶段 MPaFig.6 TQYW-6.0-2 in phase Ⅰ

Ⅱ阶段(弹塑性受力)：本阶段荷载-转角曲线呈现斜率不断减小的非线性关系，当M达到约0.5Mu时，可见面板、侧板交界近两端处开始出现中间幅度渐渐增大的波浪形鼓曲；芯管端部应力逐渐增大，与此同时，面板近两端受压区开始出现明显鼓曲，并且不断向中间发展，形成从两端出现斜向鼓曲，并逐渐向受拉区扩展；构件整体开始有明显弯曲，直至达到承载力极限水平，详见图7。可知：受压区侧板受压成波浪形屈曲，大部分面板屈服，且塑性区不断向另一边扩展，跨中开始出现较明显横向位移；部分芯管根部明显开始屈曲，逐渐失去对面板的面内外支承能力。

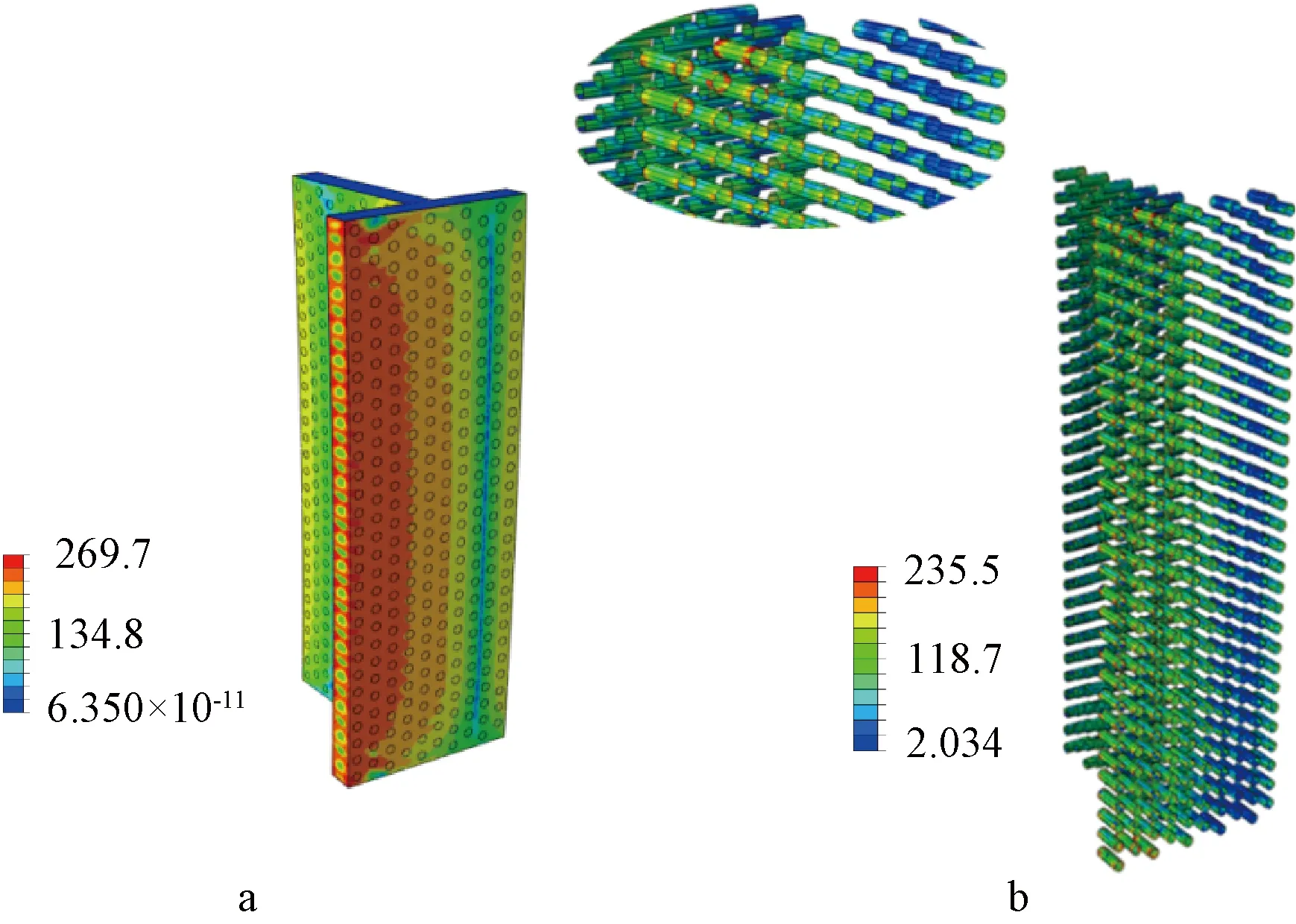
a—整体；b—芯管部分。图7 TQYW-6.0-2第Ⅱ阶段 MPa Fig.7 TQYW-6.0-2 in phase Ⅱ

Ⅲ阶段(破坏)：达到极限荷载后，受压区侧板明显鼓曲，基本退出工作；部分芯管端部接近或达到屈服应力，由于管壁过薄，且在管壁面内和近管端部法向均受压力作用，所以在接近达到屈服点时就已出现屈曲，很快就退出工作；受压区面板鼓曲进一步扩展，且大多分布于加载端附近，构件抗力下降，转角显著增大，构件破坏，详见图8。破坏时除翼缘另一端和腹板自由端局部外基本全截面受压，构件有明显弯曲，跨中挠度最大(约34 mm)，达到l/100，加载端附近由于应力集中出现明显斜向鼓曲，弯矩下降到0.85Mu时构件宣告破坏；受压区端部芯管根部受压屈曲，完全失去对面板的支承作用。

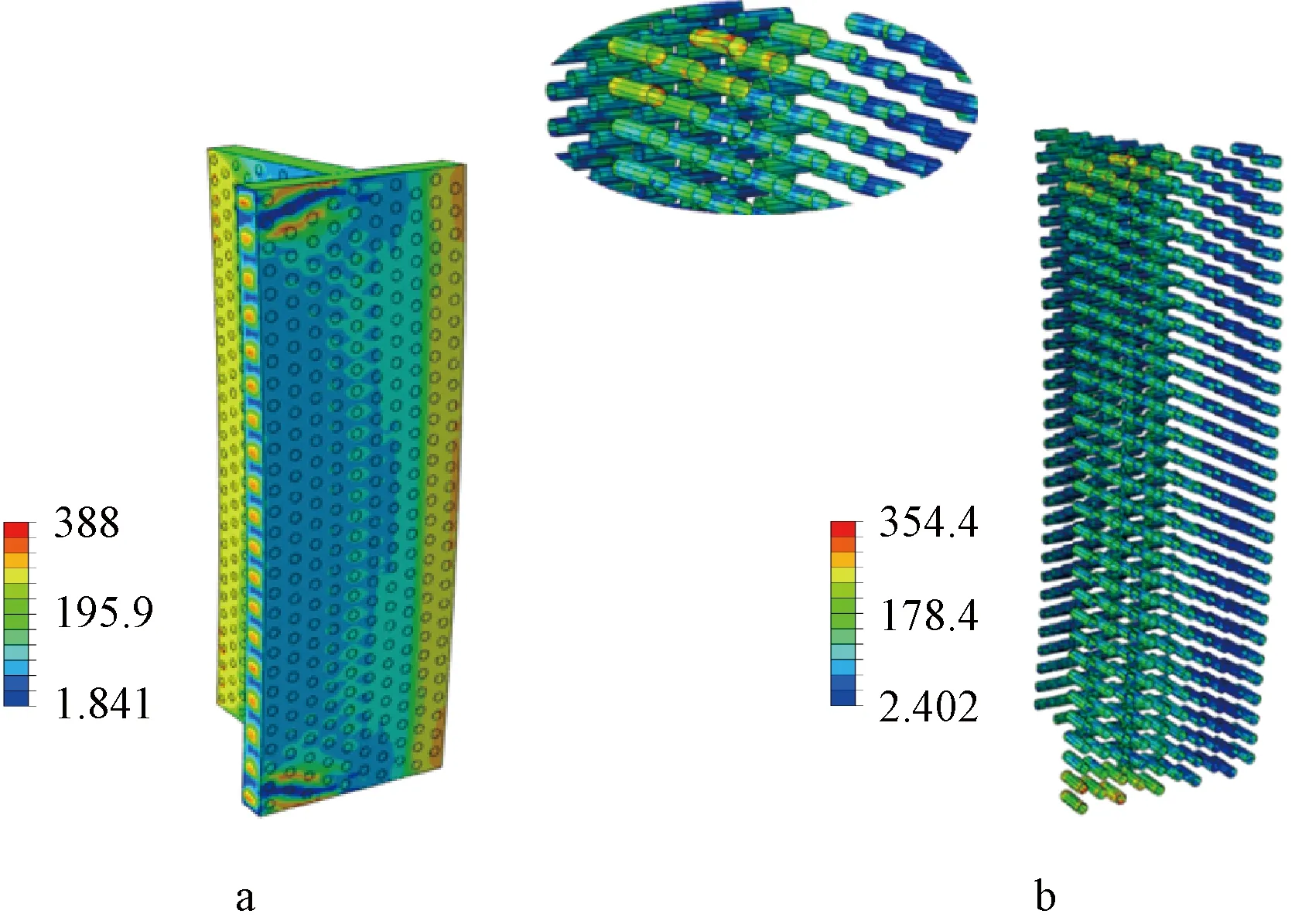
a—整体；b—芯管部分。图8 TQYW-6.0-2 第Ⅲ阶段 MPaFig.8 TQYW-6.0-2 in phase Ⅲ

试件TQYW-2.5-1～3和TQYW-4.0-1～3由于面板板厚度较小，导致其屈曲较早发生，且在破坏前，整体失稳不明显，主要是由于加载端部附近压应力较大导致该区域局部屈曲过早发生，以致于弯矩不能有效从两端传递至中间。试件TQYW-8.0-1～3由于面板厚度较大，导致侧板屈曲要远远早于面板发生，破坏时构件整体弯曲程度也大于其他构件，除此之外，破坏过程均与试件TQYW-6.0-2类似，此处不再赘述。

从全部12组模型破坏全过程来看，不锈钢芯板T形墙受双向压弯荷载下的破坏本质是：结构进入弹塑性阶段后，受压区近加载端压应力已经超过不锈钢屈服强度，由于芯管端部对面板面内外的支承作用和侧板的端部约束以及帮助面板支持荷载的作用，使得面板屈曲速度大大减缓，直到侧板屈曲过于严重失去约束和承载能力，芯管端部发生屈曲不能再提供面内外支承，受压区面板彻底失去支承从而屈曲范围迅速扩展，构件宣告破坏。

3 双向压弯承载力参数分析

主要研究以下几种参数对不锈钢芯板T形墙双向压弯承载力产生的影响：轴压比n、高宽比β、面板厚tm、侧板厚tc、芯管厚tx。

3.1 轴压比n

T形墙所承受的轴压力大小直接影响T形墙各方面受力性能，因此研究轴压比n的大小对于墙受双向压弯下的极限抗弯承载力的影响是控制轴压比设计的重要环节[14]，轴压比同时也是研究T形柱抗震性能的重要参数[15]。以tm=8 mm为例，偏心角θ取为15°、45°、75°、105°、135°、165°，轴压比n在0～1.2内等距取13个点，计算了共计78个数值算例，对得出数据进行整理，如图9所示。

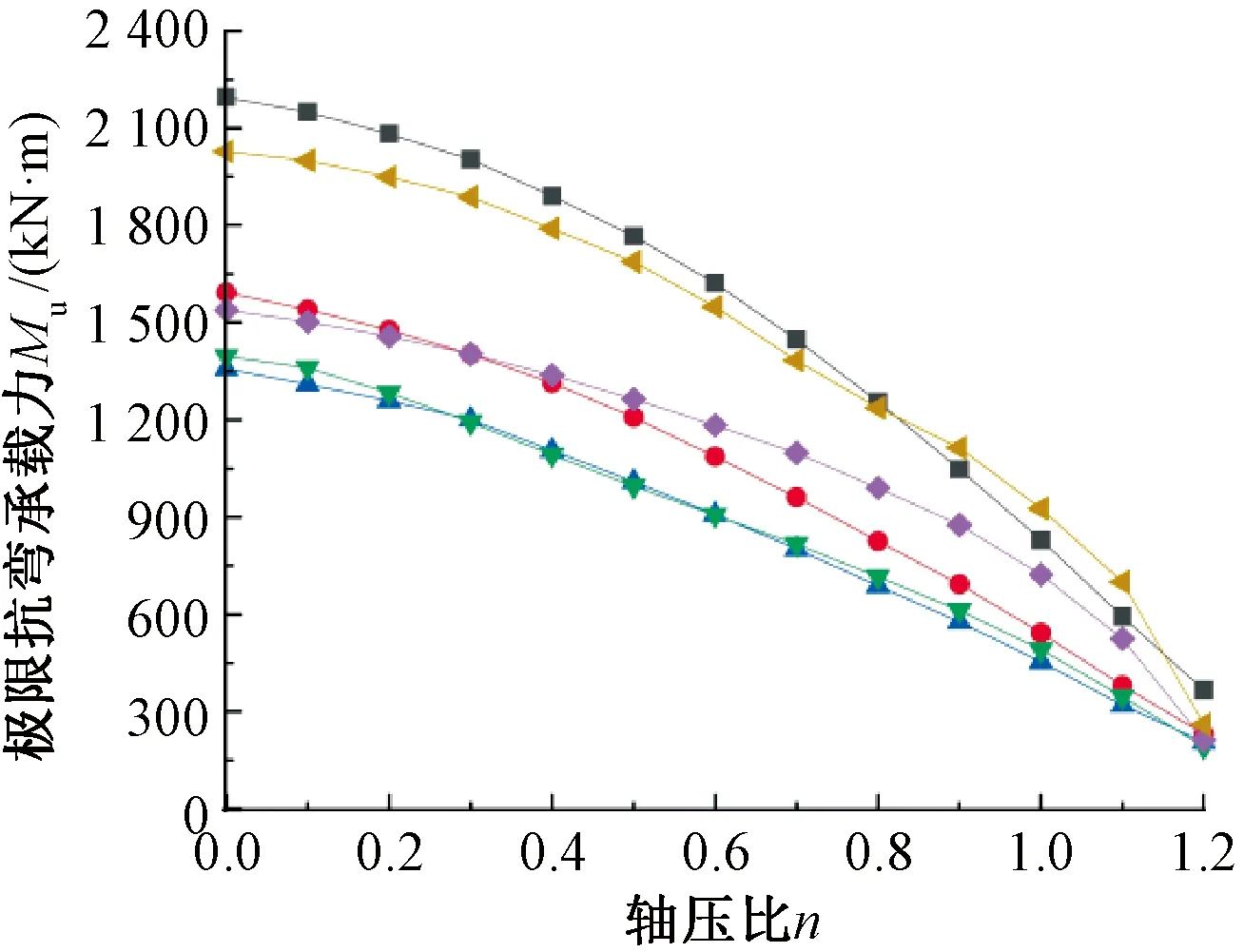
θ=15°； θ=45°； θ=75°； θ=105°； θ=135°； θ=165°。图9 不同轴压比对双向受弯极限承载力Mu的影响Fig.9 Influence of different axial compression ratios on the ultimate bearing capacity Mu in biaxial bending

根据图9可知，不锈钢芯板T形墙在受到双向压弯荷载作用下，随着轴压比的增大，极限抗弯承载力不断减小，没有像普通钢筋混凝土柱或者型钢混凝土柱一样存在界限轴压比。主要是因为纯不锈钢薄壁柱在压弯荷载作用下，由于不锈钢的抗拉强度大，塑性变形能力很强，总是以受压区先发生屈曲导致构件破坏。

3.2 高宽比β

保持面板厚tm=6 mm，侧板厚tc=2.5 mm，芯管厚tx=0.5 mm，偏心角θ=120°不变，取轴压比为0.1、0.3、0.5、0.7、0.9，墙高分别取3，4，5，6 m，高宽比β分别为3，4，5，6。针对高宽比β建立20组数值分析模型，将计算结果进行整理，如图10所示。

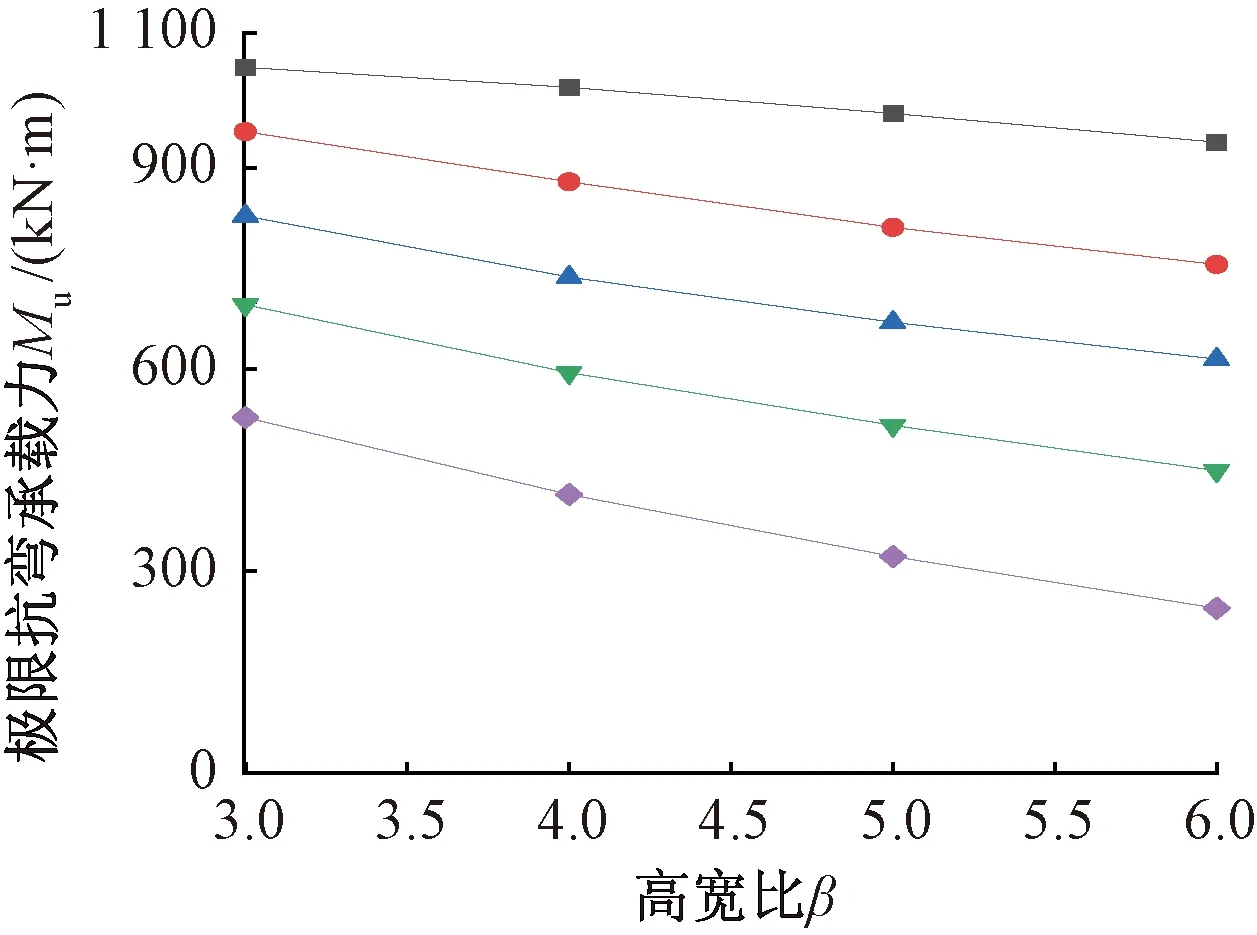
n=0.1； n=0.3； n=0.5； n=0.7； n=0.9。图10 不同高宽比对双向受弯极限承载力Mu的影响Fig.10 Influence of different aspect ratios on the ultimate bearing capacity Mu in biaxial bending

根据图10可以得出结论：在轴压比不变的情况下，随着高宽比β的增加，极限抗弯承载力随之减小，而且这种影响随着轴压比n的增大而增大；β从3.0增大至6.0的过程中，轴压比n=0.1、0.3、0.5、0.7、0.9时，极限抗弯承载力分别下降约10.6%、20.7%、25.7%、35.4%、53.6%，这主要是由于墙的高度增加，组成T形墙的主要部件——面板，在施加压弯荷载的过程中跨中挠度也增大，轴力产生的附加弯矩也随之增大，最终导致极限弯矩的减小。

3.3 面板厚度tm

保持其他截面参数不变，固定轴压比为0.4，取偏心角为0°～180°，以15°为间隔，即0°、15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°、180°，面板厚度tm为2.5，4，6，8 mm，针对面板厚度tm建立52组数值模型,将最后所得结果整理汇总成曲线，如图11所示。

根据图11可知：面板厚度变化对于T形墙极限抗弯承载力Mu有着极大影响，面板厚度从2.5 mm增加到4 mm时，平均极限抗弯承载力Mu增加约144%；增加至6 mm时，Mu增加约322.9%；增加至8 mm时，Mu增加约468%。之所以Mu的增长速度明显高于面板厚度增长速度，主要是面板作为不锈钢芯板T形墙截面最主要受力部分，不论偏心角多少，面板厚度的提高对于全截面惯性矩的提高速度都是超过线性增长速度的。偏心角对T形墙极限抗弯承载力有一定影响，除tm=2.5 mm之外，其他面板厚度下，弯矩作用平面与腹板所在平面夹角越小，极限抗弯承载力越大，产生该现象的成因主要是T形墙沿强轴和弱轴的惯性矩大小不同，导致沿两轴的极限抗弯承载力存在显著差异。

tm=2.5 mm； tm=4.0 mm； tm=6.0 mm； tm=8.0 mm。图11 不同偏心角下面板厚度对双向受弯极限承载力Mu的影响Fig.11 Influence of the thickness of the panel on the ultimate bearing capacity Mu in biaxial bending under different eccentric angles

保持其他截面参数不变，固定偏心角为60°，轴压比取0.1～0.4(0.05为间隔)，0.5～0.8(0.1为间隔)面板厚度仍为2.5，4，6，8 mm，针对面板厚度tm建立44组数值分析模型，整理结果汇总如图12所示。

tm=2.5 mm； tm=4.0 mm； tm=6.0 mm； tm=8.0 mm。图12 不同轴压比下面板厚度对双向受弯极限承载力Mu的影响Fig.12 Influence of the thickness of the panel on the ultimate bearing capacity Mu in biaxial bending under different axial compression ratios

3.4 芯管厚度tx

不锈钢芯板结构的主要特色之一就是采用圆筒状芯管布置于面板之间形成面外支撑。对于芯管的分布和厚度，远大可建有限公司也进行了大量的试验分析，结果显示，对于作为楼板的不锈钢芯板结构，芯管厚度tx超过0.5 mm后，对于板的强度和抗弯刚度提高就不明显了，出于经济性考虑，远大可建有限公司生产的用作组装T形墙的芯板的芯管tx一律为0.5 mm。考虑到芯管厚度过大后，芯管和面板之间的连接钎料易于在接头间隙填充不均匀[16]，从而形成有缺陷的连接焊缝，因此本文仅设计了tx为0.5，0.8，1.1，1.4，1.7，2.0 mm共6种厚度的芯管壁厚，固定轴压比n=0.3，偏心角θ=30°，考察芯管厚度tx对不锈钢芯板T形墙受双向压弯下承载力的影响。

根据图13可得出，随着芯管厚度在一定范围内的增加，不锈钢芯板T形墙在受各种加载角度下的双向压弯荷载时的抗弯承载力均有所提高，但是提高幅度不大，2.5，4，6，8 mm四种厚度面板的T形墙，芯管厚度tx从0.5 mm增长到2 mm，其极限抗弯承载力分别增长了14.95%、6.67%、4.01%、5.95%，且基本随着芯管厚度的增长呈现线性增长。由此可见，采用增加芯管厚度来提高T形墙双向压弯承载力，效果不佳。

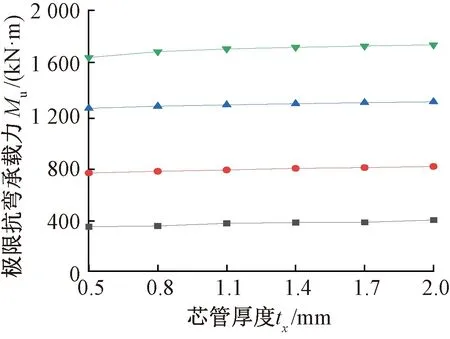
tm=2.5 mm； tm=4.0 mm； tm=6.0 mm； tm=8.0 mm。图13 不同面板厚度下芯管厚度对双向受弯极限承载力Mu的影响Fig.13 Influence of core tube thickness on the ultimate bearing capacity Mu in biaxial bending under different panel thicknesses

3.5 侧板厚度tc

保持面板厚度tm为6 mm不变，偏心角30°不变，设定轴压比n分别为0.1、0.25、0.4、0.55、0.7，侧板为2.5,4,6,8 mm四种厚度，考察在不同轴压比下，侧板厚度tc的增加对T形墙极限受弯承载力的影响，整理数据汇总如图14所示。

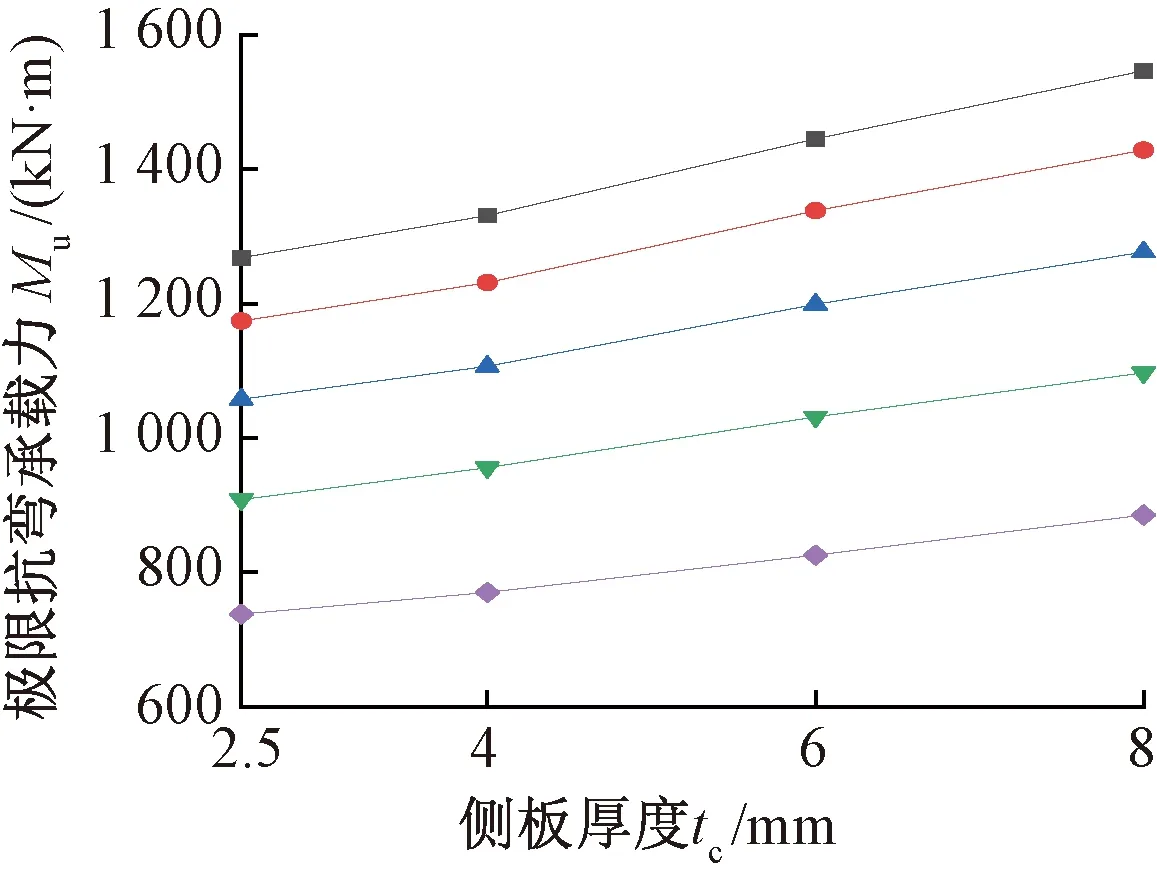
n=0.10； n=0.25； n=0.40； n=0.55； n=0.70。图14 不同轴压比n下侧板厚度对双向抗弯极限承载力Mu的影响Fig.14 Influence of the thickness of the lower side plate on the ultimate bearing capacity Mu in biaxial bending with different axial compression ratios

根据图14曲线可知，同一轴压比下，侧板厚度的增加对压弯构件的极限抗弯承载力Mu有一定的提升作用，tc的增长与Mu增长近似成线性关系，不仅仅是由于其对两轴惯性矩的影响，主要是由于在受压区，侧板位于压弯荷载产生的叠加压应力最大处，侧板的加厚使得自身宽厚比减小，尤其当宽厚比从大于规范[16]限值减小到限值以内时，侧板可作为全截面有效的部分加劲板件或者非加劲板件设计，同时更加不易发生受压屈曲，更加充分发挥强度，尤其给受压区面板的边缘提供了有效的面外支承，延缓了其受压屈曲的进程。

保持轴压比n=0.4不变，偏心角30°不变，分析在不同面板厚度下，侧板厚度分别为2.5,4.0,6.0,8.0 mm四种厚度时对极限抗弯承载力的影响，整理数据汇总如图15所示。

tm=2.5 mm； tm=4.0 mm； tm=6.0 mm； tm=8.0 mm。图15 不同面板厚度下侧板厚度对双向受弯极限承载力Mu的影响Fig.15 Influence of side plate thickness on the ultimate bearing capacity Mu in biaxial bending under different panel thicknesses

当面板厚度分别为2.5，4.0，6.0，8.0 mm，侧板厚度从2.5 mm增长到8 mm时，极限抗弯承载力分别增长了65.6%、29.3%、20.7%、16.8%，说明随着面板厚度增加，增加侧板厚度对极限抗弯承载力的贡献越来越小。

4 Mx-My相互作用方程

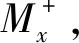
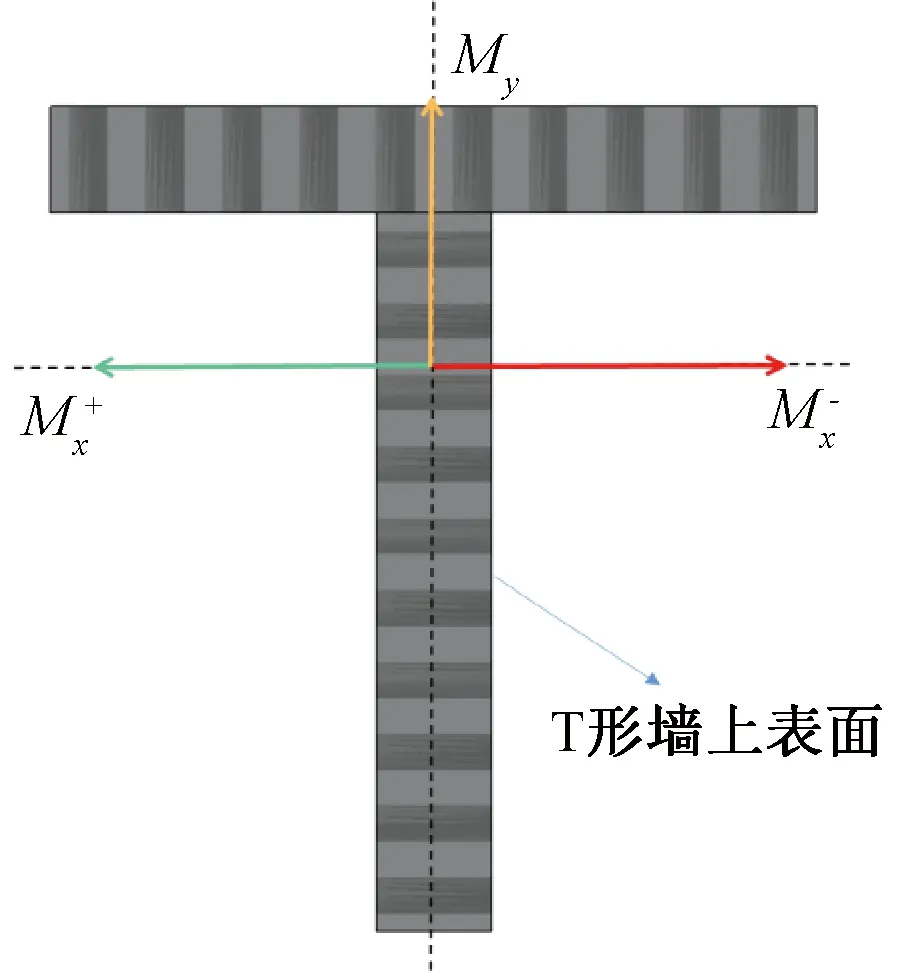
图16 弯矩方向示意Fig.16 The schematic diagram of bending moment direction

现将不锈钢芯板T形墙典型构件(tm=4 mm，tc=2.5 mm，tx=0.5 mm)在不同轴压比下的Mx、My数值计算结果进行归一化，考虑到T形墙在承受正、负向弯矩时，双向压弯关系曲线有较大区别，本文将其分开研究。拟合结果如图17所示。

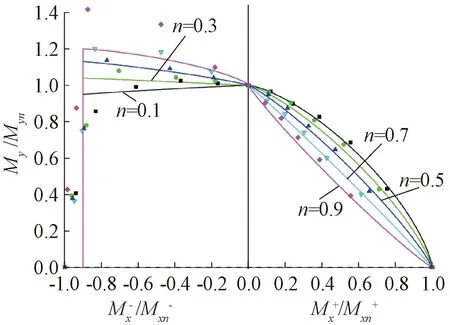
n=0.1； n=0.3； n=0.5； n=0.7； n=0.9。图17 标准构件双向压弯拟合曲线图Fig.17 Fitting curves of standard members under biaxial compression-bending

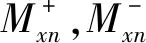
由图17可知，不锈钢芯板T形墙受压弯荷载下Mx/Mxn与My/Myn的关系与轴压比n和受弯方向密切相关，随着n的增大，不论正负向受弯，曲线凸出均逐渐减小；当受到绕x轴负向的弯曲时，由于Mx的存在使得翼缘部分受拉，从而抵消了部分由My在受压区带来的压应力，而翼缘正是主要承受My的部分，因此当n在一定范围内时会出现My/Myn>1的情况，且随着n的增大，这种放大作用愈加明显。考虑到过大的轴压比和Mx-叠加后可能会使腹板过早受压破坏，出于保守考虑，结合大量有限元分析结果，定义：

(1)

Mx-My相互作用方程如下。

负向受弯：

n1=1.16-0.6n≥0.74

(2b)

k=0.905+0.45n

(2c)

Mky=kMyn

(2d)

正向受弯：

n2=1.46-0.6n

(3b)