高强钢筋混凝土柱受弯性能的尺寸效应研究*

李振宝 于春义 解咏平 马 华 唐贞云

(1.北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124；2.河北地质大学城市地质与工程学院，石家庄 050031)

随着社会需求的不断增加，工程结构尺寸越来越大，如超高层建筑、跨海桥梁、水利工程、海洋平台、大型地下空间结构、穿山穿岭隧道以及各类核设施等。同时，结构采用的混凝土强度也越来越高，这样不仅满足承载力的要求，也满足耐久性的要求。然而，随着混凝土强度的提高，混凝土的脆性性质增强。为此，对混凝土材料科学及结构设计理论提出了更高的设计要求。特别是在地震作用下高强混凝土柱的抗震性能。一些研究分析了影响高强混凝土柱抗震性能的因素，其主要包括混凝土强度[1]、约束效应[2]、箍筋强度[3-5]、箍筋配筋率及轴压比[6-8]等。研究发现：随着混凝土强度的提高，构件延性减弱；在轴压比小于0.3时，箍筋强度的提高对延性系数和耗能能力的改善不明显，但是在轴压比大于0.4时，改善明显；随着体积配箍筋率的提高，构件延性和耗能能力增强，但随着轴压比的增大而减小。此外，文献[9-10]的研究发现：普通钢筋混凝土柱的名义弯曲应力、耗能能力及安全储备系数等抗震性能指标存在尺寸效应。文献[11-12]研究发现：高强混凝土柱受弯极限承载力存在尺寸效应，并且随着混凝土强度和剪跨比的提高，其尺寸效应更加明显。

首先了解一下经典的尺寸效应理论模型，以便于选取正确理论模型应用于工程设计。现有理论证实了混凝土材料及构件的力学性能存在尺寸效应。Griffith建立了基于断裂力学理论的尺寸效应模型，其适用于脆性材料，并且对数渐近线的斜率为-1/2[13]。随后Weibull基于韦伯分布推导了结构平均强度的尺寸效应方程，其适用于疲劳断裂的细料陶瓷和金属材料[14-15]。Bažant等创建了Type1[16-17]、Type2[18]和广义尺寸效应模型[19]，其适用于准脆性材料。在最近的研究中，Hoover等于2014推导了一种改进的广义尺寸效应模型[20]。Type1适用于在试件表面产生裂缝即发生破坏的试件[21]，其表现为混凝土受拉破坏。Type2主要适用于宏观裂纹稳定扩展之后而破坏的构件[18]，并且宏观裂纹长度大于断裂扩展区的长度，其表现为混凝土的受压破坏。改进的广义尺寸效应模型介于Type1和Type2之间，宏观裂纹的长度即不能被忽略也没有达到大于断裂扩展区的程度[21]。以上尺寸效应模型之间的关系见文献[21]。

综上所述，对高强混凝土柱受弯屈服承载力的尺寸效应尚未见报道，不同截面尺寸如何影响高强混凝土柱受弯屈服承载力仍是一个未知的问题。

1 试验概况

1.1 试件设计

试件尺寸分别为300 mm×300 mm、500 mm×500 mm和700 mm×700 mm。纵筋直径、纵筋间距、箍筋直径、箍筋间距及混凝土保护层厚度按3∶5∶7的比例进行设计。试件的保护层厚度分别为15，25，35 mm。试件尺寸及配筋如图1所示。试件设计信息见表1。

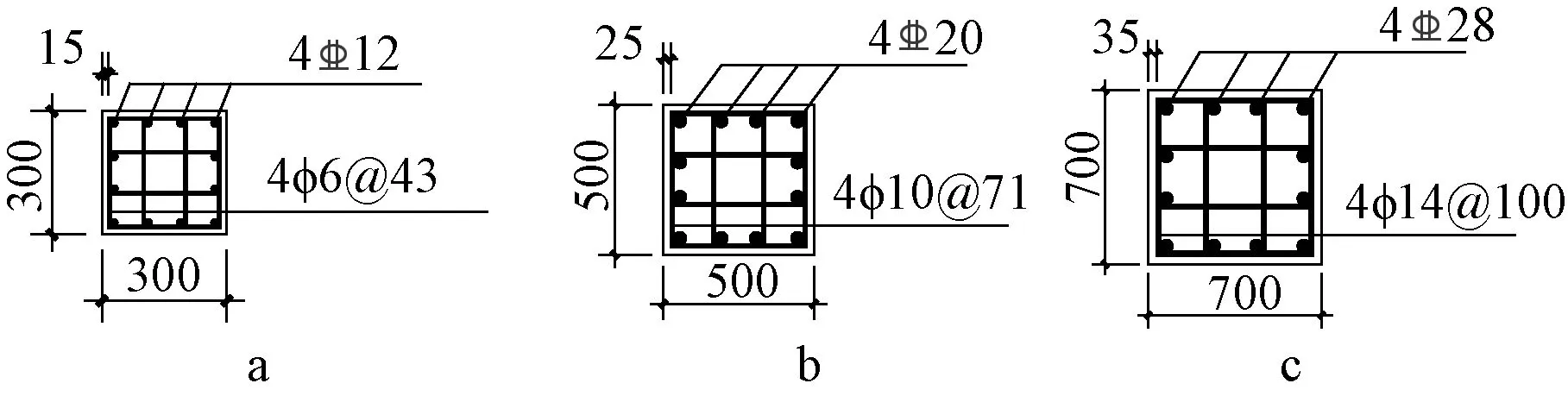
a—WD-3；b—WD-5；c—WD-7。图1 试件尺寸及配筋 mmFig.1 Sizes and reinforcement for specimens

表1 试件设计信息Table 1 Design details of the specimens

1.2 材料属性

根据GB/T 50081—2002《普通混凝土力学性能试验标准方法》[22]测定混凝土的材料属性，见表2，其包括实测的劈拉强度、混凝土轴心抗压强度和立方体抗压强度。

表2 混凝土材料属性Table 2 Material properties of concrete MPa

根据GB/T 228.1—2010《金属材料 拉伸试验 第1部分：室温试验方法》[23]测定钢筋材料属性，材料属性见表3，其主要包括实测屈服强度、抗拉强度和弹性模量。

表3 钢筋材料属性Table 3 Material properties of steel bars

1.3 试验加载制度及加载设备

1.3.1试验加载制度

试验加载制度采用荷载和位移混合控制的加载方式进行加载。水平荷载控制阶段分为5级加载，分别以屈服荷载的20%、40%、60%、80%和100%加载；屈服荷载以后采用位移加载，分别以Δy、1.5Δy、2Δy、2.5Δy，…，nΔy作为控制位移，直到荷载下降至峰值荷载的85%以下。

1.3.2试验加载设备

截面尺寸300 mm的试件由小量程作动器完成，如图2a所示。小量程加载设备的轴向最大荷载为2 000 kN，水平最大荷载为500 kN。截面尺寸500 mm和700 mm的试件由大量程作动器完成，如图2b所示。大量程加载设备的轴向最大荷载为40 000 kN，水平最大荷载为4 000 kN。试件的试验轴压比均为0.4。

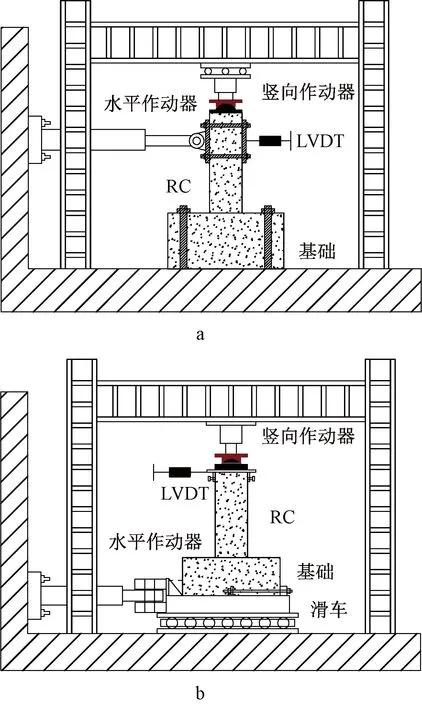
a—试件尺寸300 mm的加载设备；b—试件尺寸500 mm和700 mm的加载设备。图2 试验加载设备Fig.2 Loading setup

1.4 测点布置

应变片的布置如图3所示。根据纵筋和箍筋的应变值判断试件的力和变形情况。纵筋布置五层应变片，箍筋布置两层应变片。

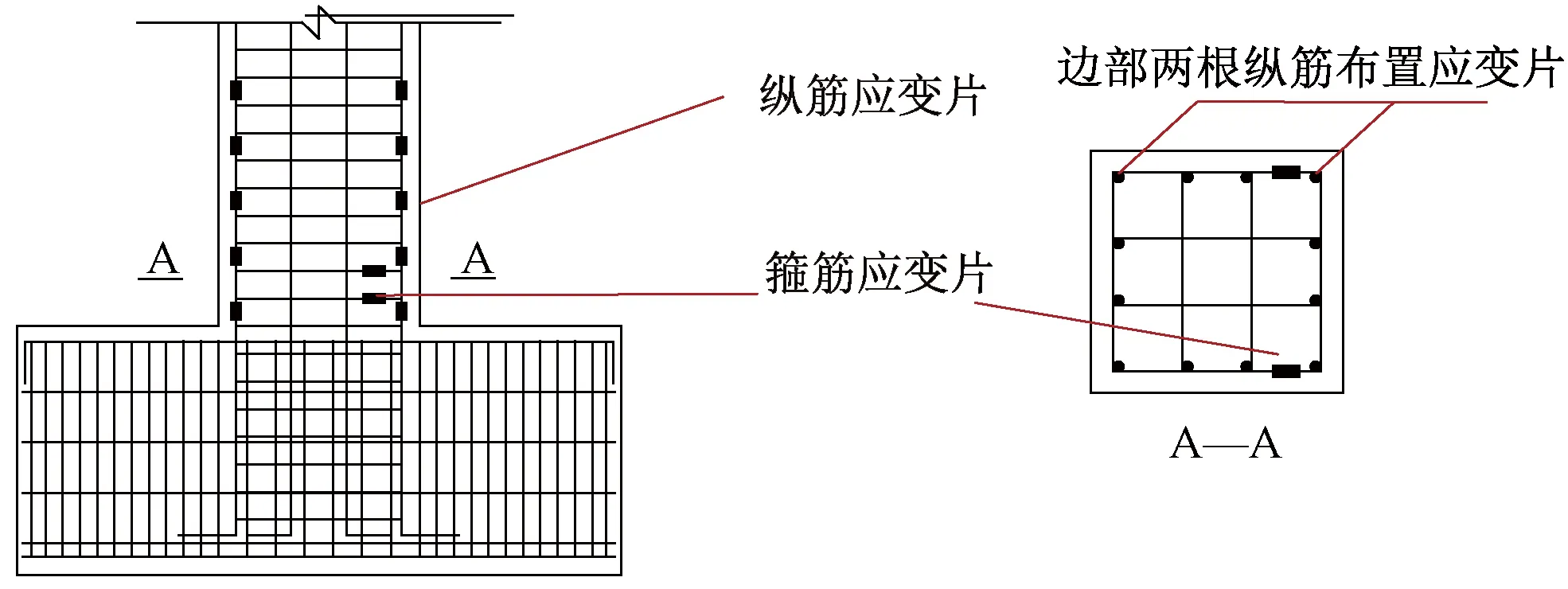
图3 纵筋及箍筋应变测点布置Fig.3 Arrangements of strain measurement points on the longitudinal rebars and stirrups

2 试验结果及分析

2.1 试件破坏特征

试件的破坏特征如图4所示，其主要给出了三个荷载时刻的试件破坏特征，其包括屈服荷载、峰值荷载及破坏荷载，其中，破坏荷载为峰值荷载的85%[24]。网格尺寸大小为50 mm，其总高度为柱截面高度。试件的破坏特征如下：

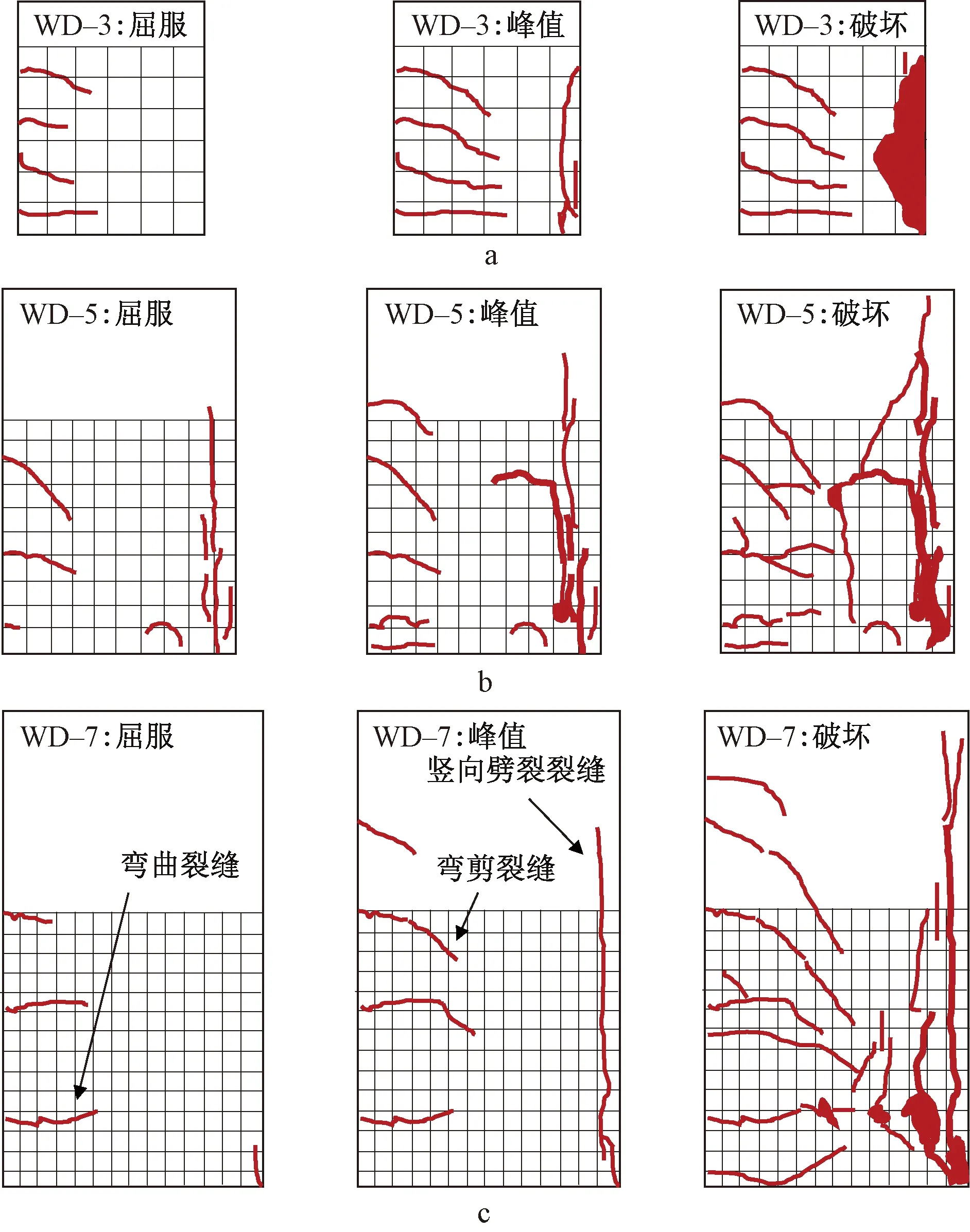
a—截面尺寸300 mm试件；b—截面尺寸500 mm试件；c—截面尺寸700 mm试件。图4 试件的破坏特征Fig.4 Failure characteristics for specimens

1)当试件达到屈服荷载时，弯矩最大截面出现一条弯曲裂缝，上部出现弯剪裂缝，并且弯剪裂缝角度较小；当试件达到峰值荷载时，弯剪裂缝的角度达到最大，近似为45°；当试件达到破坏荷载时，弯剪裂缝基本不再向上扩展，而是继续延伸、变宽，最终，弯剪裂缝的条数大致为4～7条。

2)当试件达到屈服荷载时，受压区产生一条较小的竖向劈裂裂缝；特别对于大尺寸试件WD-7，当试件达到峰值荷载时，产生明显的竖向劈裂裂缝；当试件达到破坏荷载时，竖向劈裂裂缝加宽，同时其向上延伸，并且向中性轴发展，压区混凝土压碎。

2.2 荷载-位移关系

柱的水平荷载-位移关系如图5所示。从图中可知，当大尺寸试件达到峰值荷载时，由于混凝土保护层与核心混凝土突然分离，试件WD-7出现短小的平台段，这种影响与试件竖向劈裂裂缝明显出现的时刻相对应，进而说明混凝土保护层与核心混凝土分离可能是尺寸效应产生的原因。

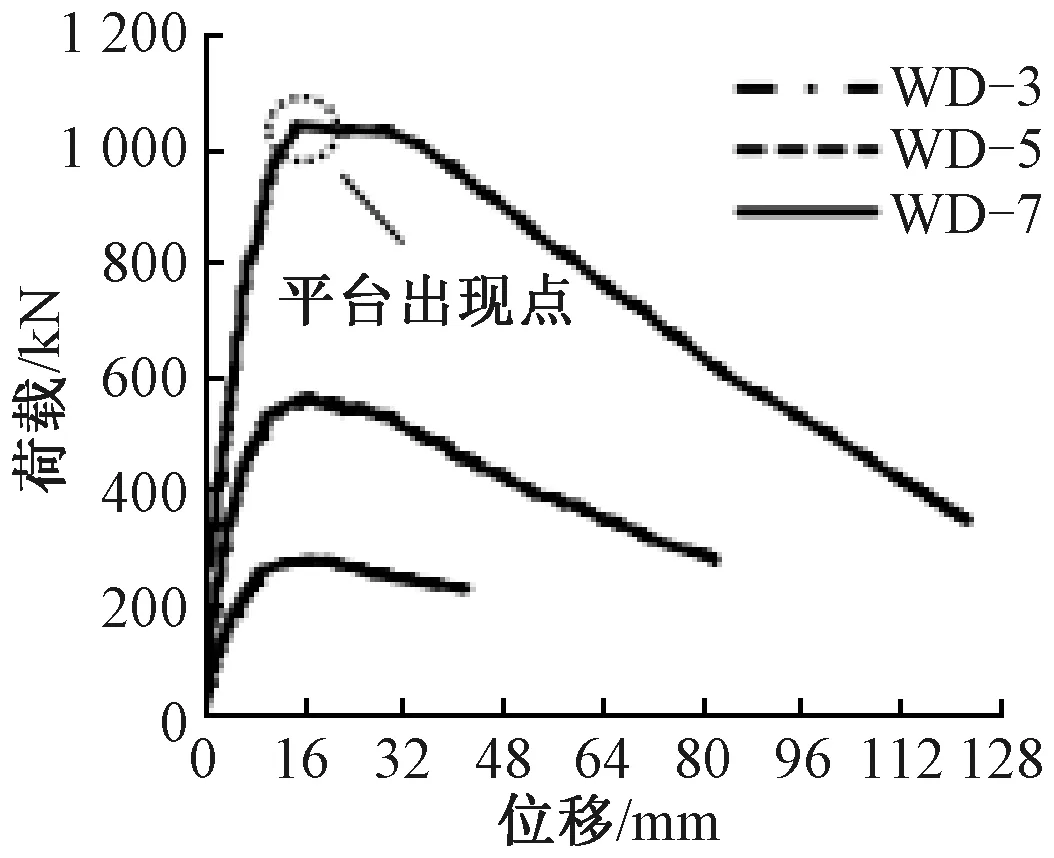
图5 荷载-位移曲线Fig.5 Load-displacement curves

从图5可知，由于轴向荷载的作用，试件没有明显的开裂荷载点。因此，将屈服荷载、峰值荷载和破坏荷载作为特征点。屈服荷载及破坏荷载计算方法如图6所示。采用能量等值法确定屈服点Y的位移，即面积BYC=OAB。然后，根据屈服位移与荷载-位移曲线的交点确定屈服荷载。破坏荷载取峰值荷载的85%[24]。Py、Pm和Pu分别为屈服荷载、峰值荷载和破坏荷载，而Δy、Δm和Δu分别为屈服荷载、峰值荷载和破坏荷载所对应的位移，计算结果见表4。从表可知，计算出的屈服荷载为峰值荷载的84%～89%。试件的延性系数在4以上。

图6 特征点的计算Fig.6 Calculation of characteristic points

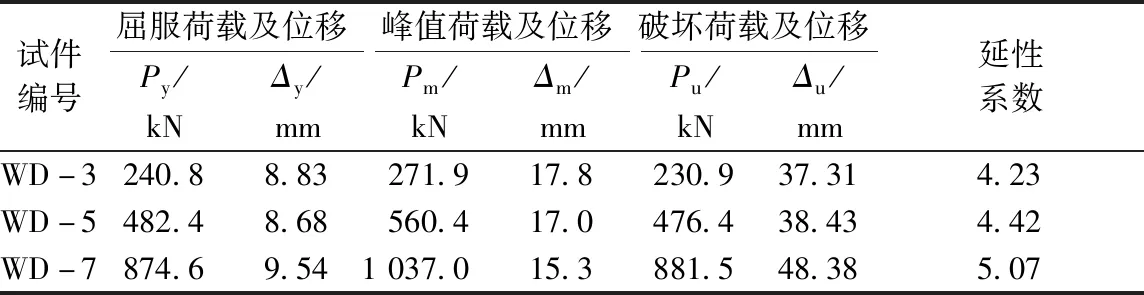
表4 试件的荷载特征值及位移Table 4 Characteristic values of load and displacement for specimens

2.3 纵筋及箍筋应变

柱根部受拉、压纵筋应变和位移的关系如图7所示。从图中可知，在峰值荷载时刻，受拉、压纵筋应变达到了屈服应变；在屈服荷载时刻，试件WD-3和WD-7的受压纵筋应变达到屈服应变，试件WD-5的受压纵筋未达到屈服；在屈服荷载时刻，受拉纵筋应变均未达到屈服应。

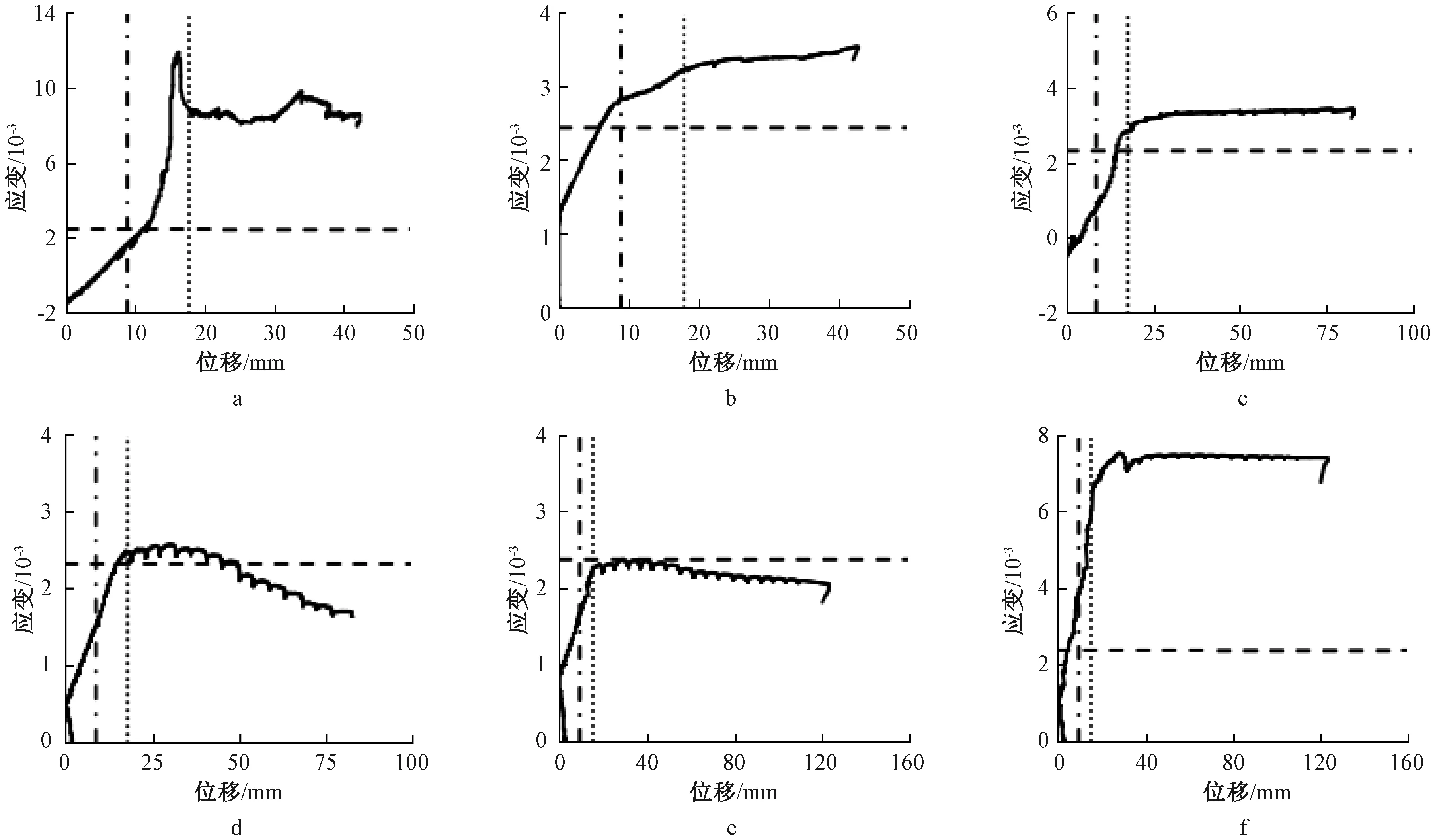
a—WD-3的受拉纵筋；b—WD-3的受压纵筋；c—WD-5的受拉纵筋；d—WD-5的受压纵筋；e—WD-7的受拉纵筋；f—WD-7的受压纵筋。---屈服应变；—·—屈服位移；……峰值位移。图7 柱根纵筋应变Fig.7 Strains of longitudinal rebars for the end of column

箍筋应变和位移的关系如图8所示。图8a中“1-43”“2-43”表示箍筋应变片距离柱根部的距离，其他含义类似。从图中可知，在峰值荷载和屈服荷载时刻，箍筋应变均远没有达到屈服应变；在位移较大的时候，大尺寸试件WD-5、WD-7箍筋应变达到屈服应变，小尺寸试件WD-3箍筋应变远未达到屈服应变。

a—WD-3：第一层箍筋43 mm处；b—WD-3：第二层箍筋86 mm处；c—WD-5：第一层箍筋71 mm处；d—WD-5：第二层箍筋142 mm处；e—WD-7：第一层箍筋100 mm；f—WD-7：第二层箍筋200 mm。图8 箍筋应变Fig.8 Strains of stirrups

3 截面尺寸对弯曲性能的影响

3.1 名义弯曲应力

考虑二阶效应的柱端弯矩为：

M=PΔ+VH

(1)

其中Δ=Δ0H/H0

式中：P为轴力；Δ为水平位移；Δ0为柱理论高度H0处的位移；V为水平力；H为水平荷载作用点到柱根的距离。

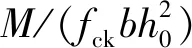
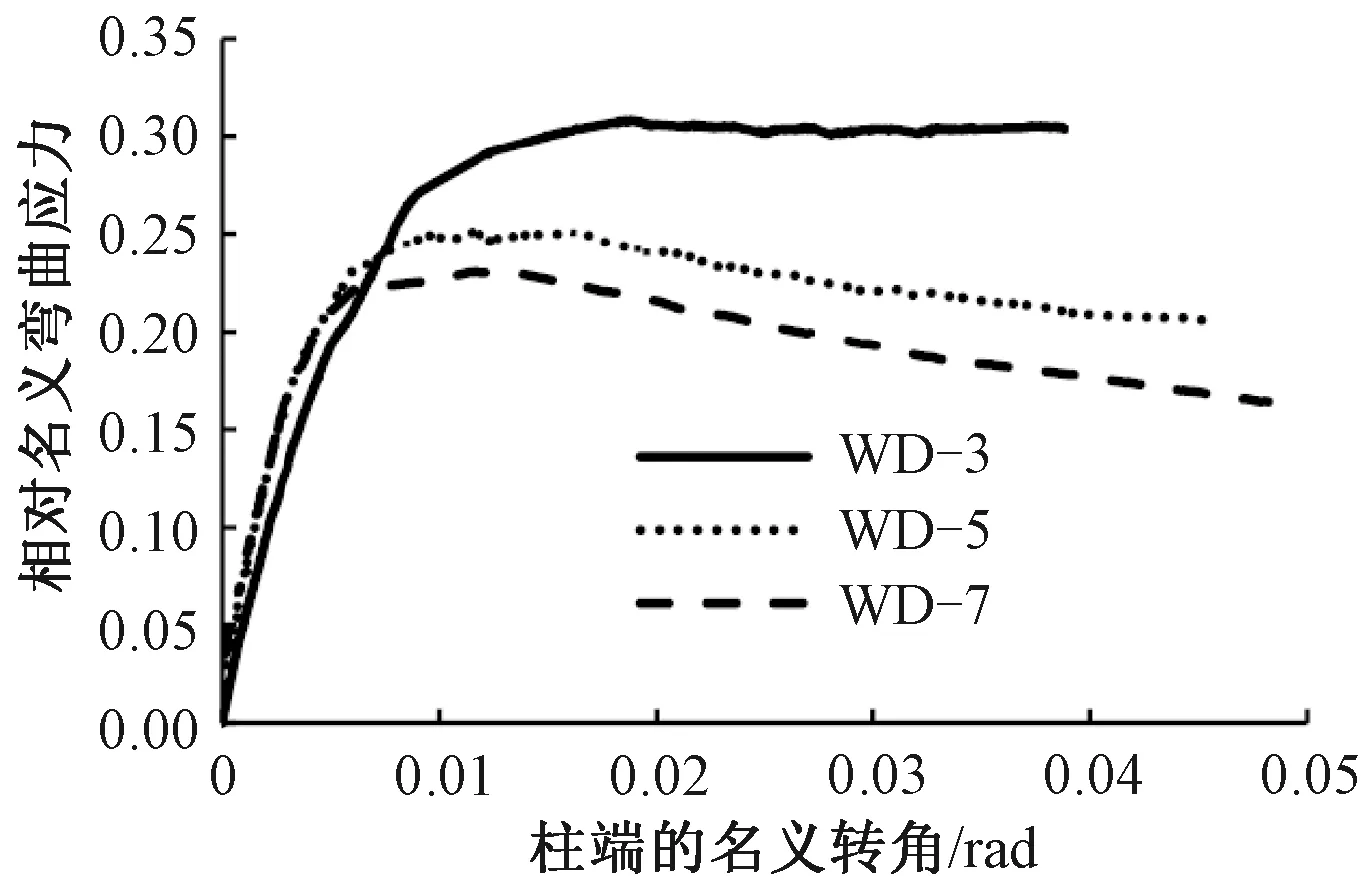
图9 相对名义弯曲应力和转角的关系Fig.9 Relations between nominal flexural stress and nominal angle of rotation

图10 截面尺寸对相对名义弯曲应力的影响Fig.10 Effects of section size on relative nominal flexural strain

3.2 名义转角

为了反映试件的转动能力，采用名义转角作为评价指标。在试件以小角度变形的条件下，名义转角近似等于水平位移与柱高的比值Δ0/H0。截面尺寸对名义转角的影响如图11所示。从图中可知，在屈服、峰值及破坏荷载时刻，随着截面尺寸的增大，试件的名义转角均减小。在三个荷载时刻，从最小到最大截面试件的名义转角分别减小了54%、63%和44%，其中，峰值荷载时刻的尺寸效应最为明显。因此，建议大尺寸试件的层间位移角限值在设计时应该进行折减。

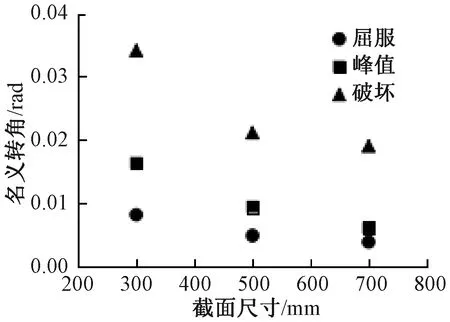
图11 截面尺寸对名义转角的影响Fig.11 Effects of section size on nominal angle of rotation

3.3 P-Δ效应

二次弯矩比为：

(2)

式中：V为水平力；P为轴力；Δ为水平位移；H为水平荷载作用点到柱根的距离。

二次弯矩比和柱端名义转角的关系如图12所示。从图中可知，随着名义转角的增大，二次弯矩比增大。对于截面为300 mm的试件，三个荷载时刻的二次弯矩比分别为7%、12%和25%；对于截面为500 mm的试件，三个荷载时刻的二次弯矩比分别为5%、8%和18%；对于截面为700 mm的试件，三个荷载时刻的二次弯矩比分别为4%、5%和17%。从上述分析可知，二阶效应在屈服和峰值荷载占比相对较小，并且从屈服到峰值时刻变化不大，而到破坏荷载时刻二阶效应变化明显。

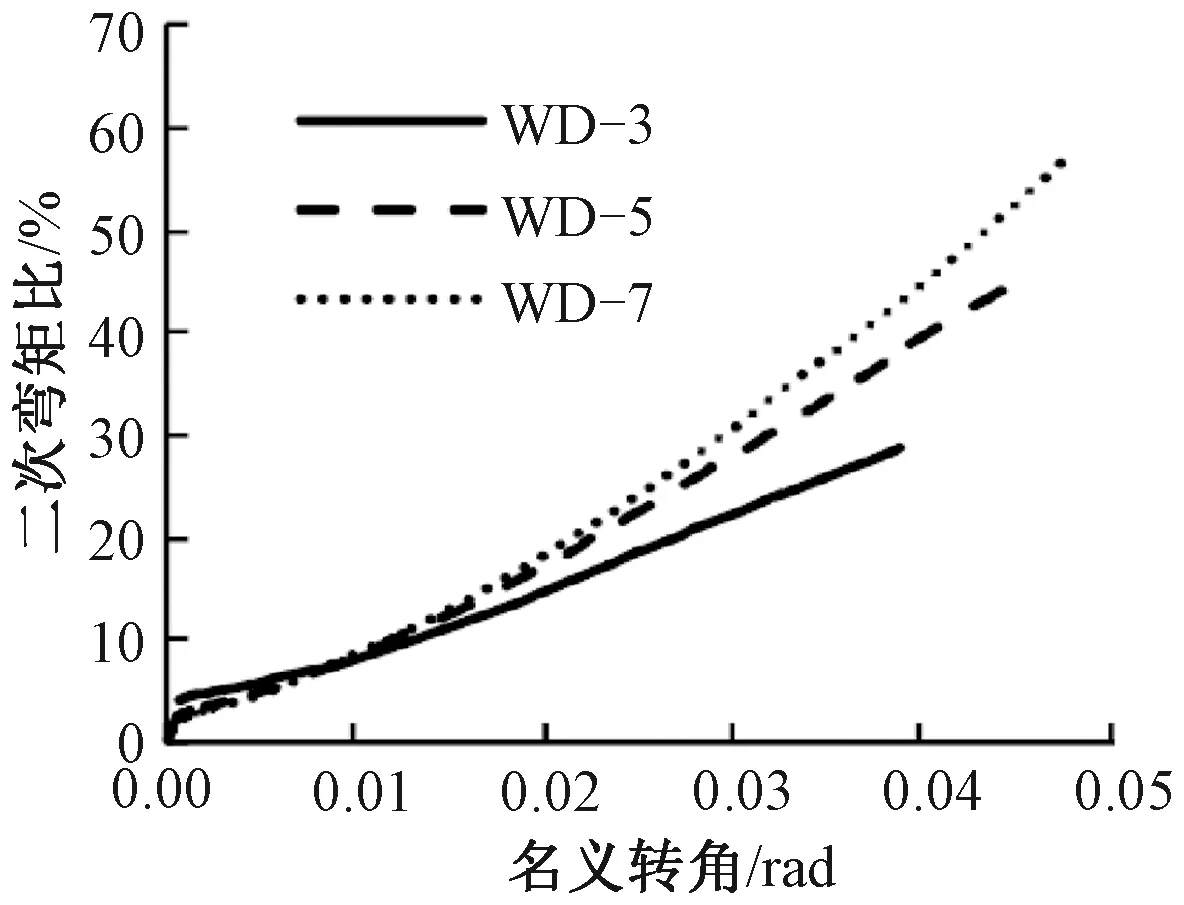
图12 二次弯矩比和名义转角的关系Fig.12 Relations between secondary bending moment and nominal rotation

图13给出了屈服、峰值和破坏荷载时刻的二次弯矩比与截面尺寸的关系。从图中可知，随着截面尺寸的增大，二次弯矩比减小，并且从最小到最大截面尺寸试件的二次弯矩比分别减小了43%、58%和32%，其中，峰值荷载时刻的尺寸效应最为明显。研究表明：二次弯矩比随着截面尺寸的增大而减小，试件的变形能力随着截面尺寸的增大而减弱。

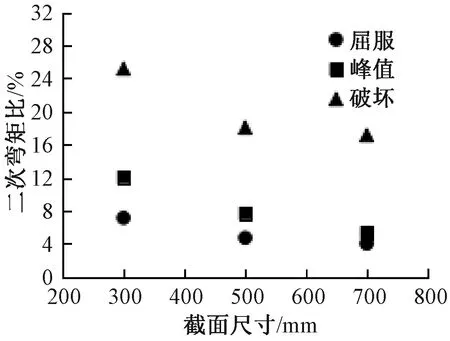
图13 截面尺寸对相对名义弯曲应力的影响Fig.13 Effect of section size on relative nominal flexural stress

4 考虑尺寸效应的受弯屈服承载力

4.1 受弯屈服承载力的理论计算

当边部受压钢筋先达到屈服强度时，受弯屈服承载力的计算简图如图14所示，而当边部受拉钢筋先达到屈服强度时的计算简图这里不再给出。根据轴向力的平衡得：

σ′s1A′s-σs1As-σs2As

(3)

当边部受压钢筋先达到屈服强度时，对几何中心取矩的受弯屈服承载力为：

Mcy=Mc+Ms

(4)

(4a)

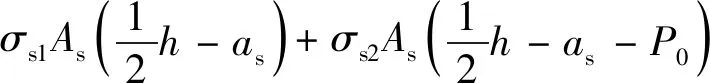
(4b)

式中：Mc为混凝土部分承担的弯矩；Ms为钢筋部分承担的弯矩;m为中性轴到几何中心的距离。

当边部受拉钢筋先达到屈服强度时，对几何中心取矩的受弯屈服承载力为：

Mcy=Mc1+Ms1

(5)

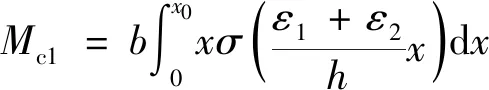
(5a)

Ms1=Ms

(5b)

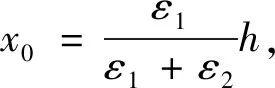
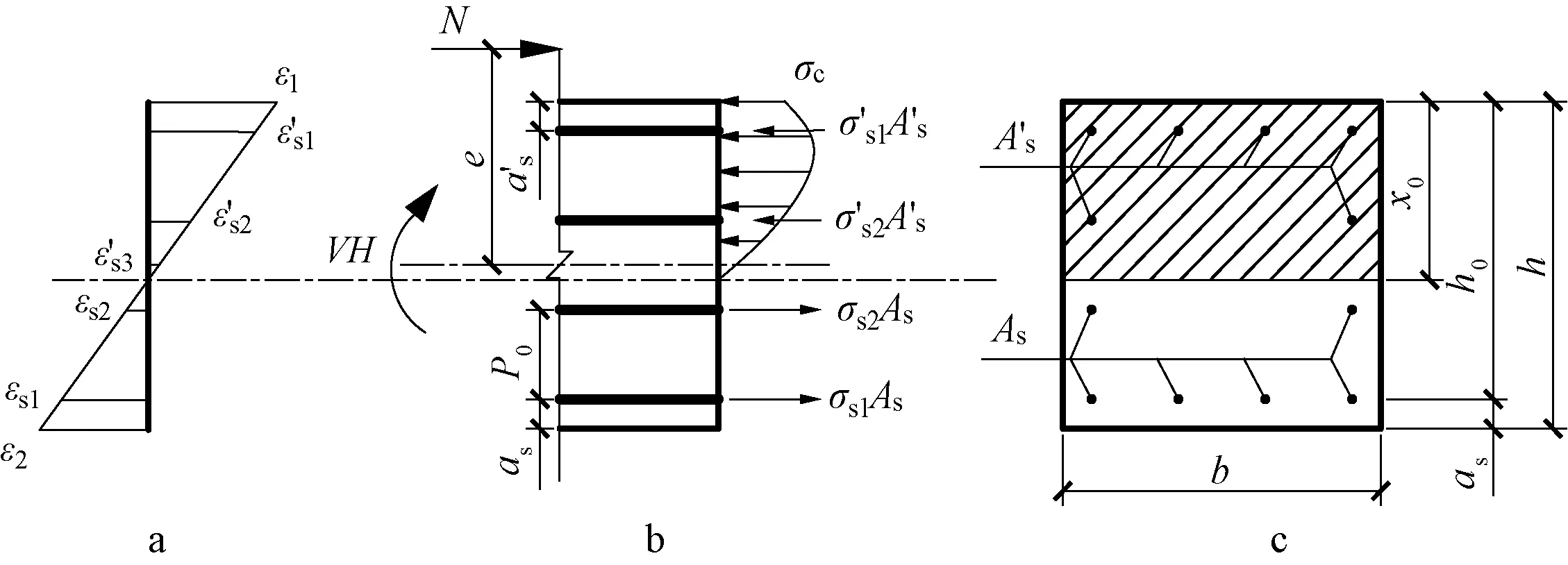
a—截面应变；b—截面应力；c—截面。σc为混凝土受压边缘的应力。图14 正截面受弯承载力的计算简图Fig.14 Moment capacity calculation diagram of the flexural capacity of the normal section

受压钢筋σ′s1和σ′s2的计算式分别为：

(6a)

(6b)

式中：ε1和ε2分别为截面受压和受拉边缘的应变；Es为钢筋弹性模量。

受拉钢筋σs1和σs2的计算式分别为：

(7a)

(7b)

当边部受压钢筋达到屈服强度时，形心处的应变为：

(8)

当边部受压钢筋达到屈服强度时，中性轴到几何中心的距离m为：

(9)

当边部受压钢筋达到屈服应变时，受压钢筋应变为：

(10)

式中：ε′y为受压钢筋屈服应变。

当边部受拉钢筋达到屈服应变时，受拉钢筋应变为：

(11)

为了评价截面尺寸对受弯屈服承载力的影响，采用安全储备系数α=Mty/Mcy作为评价指标，其中，Mty为试验弯矩；Mcy为理论计算弯矩。根据材料强度计算结果可知，其符合受压钢筋先达到屈服强，所以，受弯屈服承载力根据式(4)确定。安全储备系数如表5所示。截面尺寸对安全储备系数的影响如图15所示。从图中可知，安全储备系数随着截面尺寸的增大而减小，最小到最大截面尺寸试件的安全储备系数减小了26%，可见尺寸效应的明显性。此外，根据文献[9]计算了普通混凝土受弯屈服承载力安全储备系数，并且与本文结果进行了比较。从图15中可知，高强混凝土的尺寸效应更加明显。

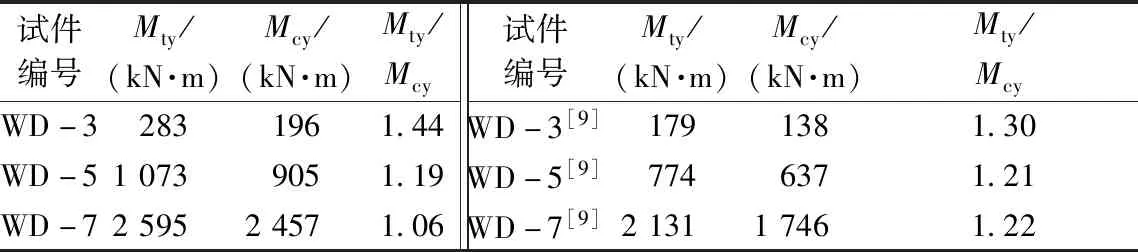
表5 安全储备系数Table 5 Safety factors

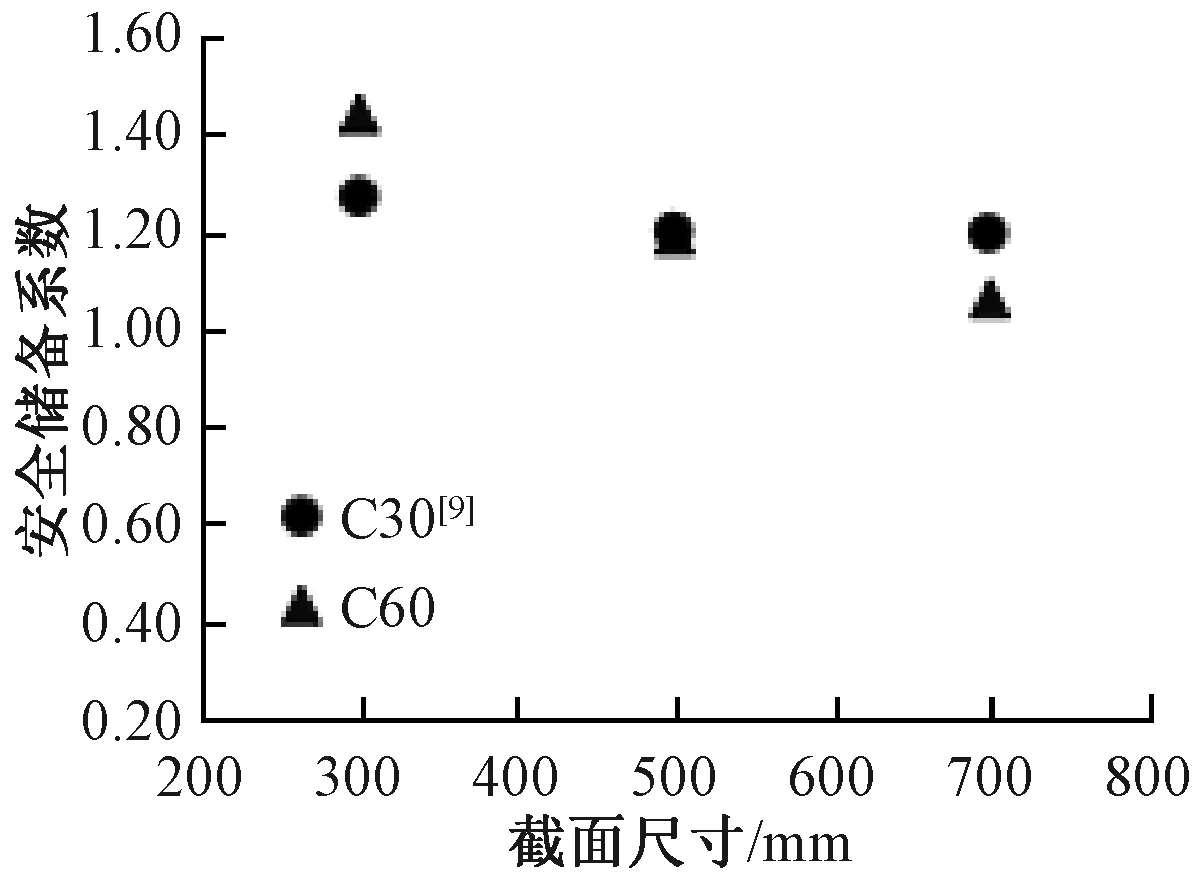
图15 截面尺寸对安全储备系数的影响Fig.15 Effects of section size on safety factors

4.2 受弯屈服承载力的修正

由试件破坏特征分析可知，其更加符合Type2[18]类型的尺寸效应模型。为了消除截面尺寸对安全储备系数的影响，本文选取Type2类型的尺寸效应理论模型来修正受弯屈服承载力。在延性金属材料中，材料的受压或者受拉破坏由斜向剪切带的塑性滑移引起，这种破坏属于延性破坏，并且不存在软化效应。一般情况下不考虑金属材料的尺寸效应[26]。因此只修正式(4)中混凝土部分承担的弯矩。

首先，由试验总弯矩计算出混凝土项所承担的弯矩为MLty。然后，由式(4)计算出混凝土承担的弯矩MLcy。将MLty/MLcy比值定义为局部安全储备系数αhD。计算结果如表6所示，可知:局部安全储备系数随着截面尺寸的增大而减小，并且从最小到最大截面尺寸试件的局部安全储备系数减小了33%，其尺寸效应明显。

表6 局部安全储备系数Table 6 Local safety factors

Type2类型的尺寸效应算式为：

(12)

式中：h为截面高度；B为试验常数；D0为延性和脆性之间的过渡尺寸；ftk为混凝土抗拉强度标准值。

由局部安全储备系数拟合求出B和D0为1.724和19.64。修正参数的计算式为：

(13)

式中：α1为最小截面的局部安全储备系数。将尺寸效应算式(13)带入式(4)得：

Mcy=αhDMc+Ms

(14)

然后，根据式(14)重新计算安全储备系数Mty/Mcy。修正后的安全储备系数如图16所示，可知：与修正前相比，修正后的安全储备系数趋于一致，进而保证大尺寸柱受弯屈服承载力计算的安全性。

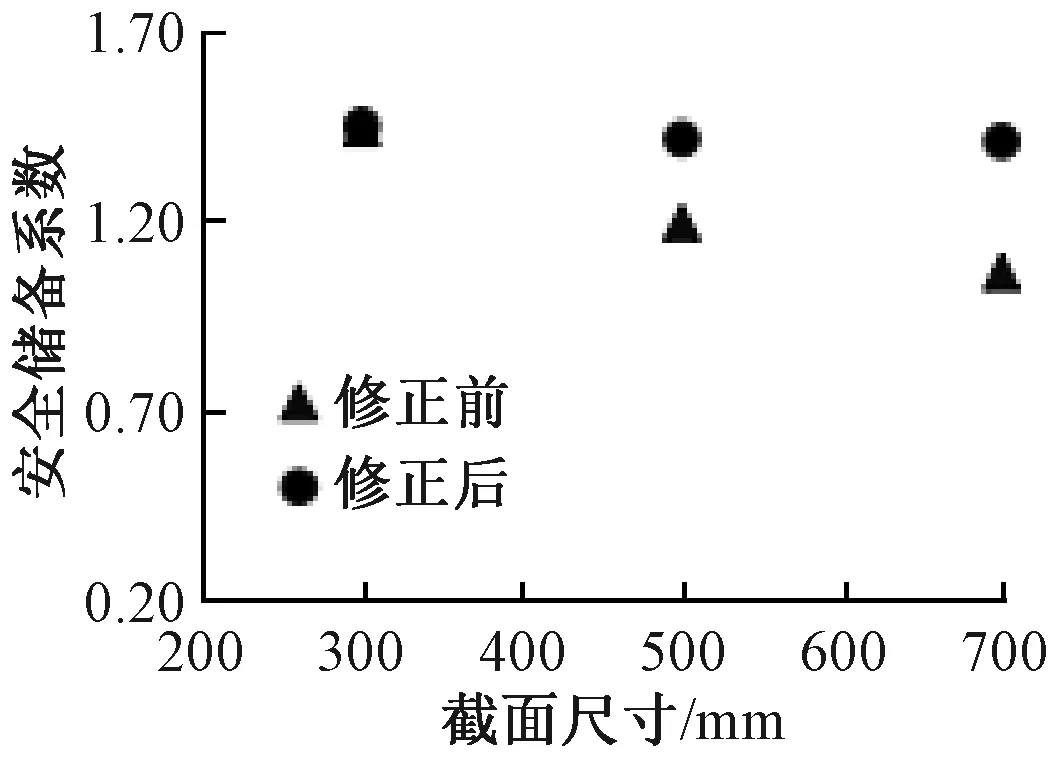
图16 修正后的不同截面尺寸的安全储备系数Fig.16 Modified safety factors for different section sizes

5 结束语

对三种不同截面尺寸的高强混凝土柱的受弯性能进行了试验研究，得到以下结论：

1)首先，柱的破坏为弯曲破坏，其表现为：在峰值荷载时刻，受拉、压纵筋应变均达到屈服应变，而箍筋应变远未达到屈服应变。其次，在屈服荷载时刻，受压纵筋应变达到屈服应变，而受拉纵筋应变未达到屈服应变。另外，在位移较大时，大尺寸试件WD-5、WD-7箍筋应变达到屈服应变，而小尺寸试件WD-3箍筋应变远未达到屈服应变。最后，大尺寸柱保护层混凝土的劈裂效应可能是尺寸效应产生的部分原因。

2)大尺寸柱的相对名义弯曲应力、名义转角、P-Δ效应及受弯屈服承载力的安全储备系数和局部安全储备系数与小尺寸柱相比均有所降低，其存在一定的尺寸效应，并且随着混凝土强度的提高，相对名义弯曲应力和受弯屈服承载力安全储备系数的尺寸效应更加明显。

3)基于试验结果和Bažant的Type2尺寸效应模型，提出了考虑尺寸效应的受弯屈服承载力计算方法。