MATLAB软件辅助高等数学的教学研究
2022-08-31杨健
杨健

摘要:该文针对高等数学课程具有概念抽象、理论深奥等特点,提出在课堂教学过程中融入Matlab软件进行探究式教学研究,通过若干具体实例来分析研究如何利用Matlab软件进行相关教学,通过软件引导学生直观理解高等数学的抽象概念,同时促使学生学习一定的编程技巧,掌握利用Matlab程序语言化简课程中的一些烦琐的计算过程,锻炼动手能力。
关键词:高等数学;Matlab软件;课堂教学;探究式教学
中图分类号 G642 文献标识码 A
文章编号:1009-3044(2022)18-0155-04
开放科学(资源服务)标识码(OSID):
在当代大学中,高等数学课程受众广泛,应用普遍,为理工科甚至文科相关专业学生学习相应专业课程提供数学工具和思想,给后续学好相关专业课程提供强大支撑。然而,高等数学本身作为一门重要数学课程,有着逻辑严密,概念抽象,理论性强,定理深奥不易理解,计算复杂等特点。这对一般的非数学专业学生来说,对课程特点的适应具有一定的难度。然而,Matlab软件集数值运算、符号运算和图形操作于一体,同时拥有多个专业工具箱,是一款具有可视化强、计算高效、功能丰富、操作简便、简单易学等特点的交互式系统软件[1]。无论对于应用工程人员,还是科研技术专家,都是一款强大而便捷的工具软件。若能抽出课堂的一部分篇幅,将Matlab软件有效合理地融入高等数学的教学中,让学生了解软件的相关功能,学会编写相应算法程序,使高等数学中抽象的定义、定理及相关概念通过图形数据的方式直观具体地展现出来,让学生深刻了解概念中的细微之处,就能化解学生在学习中的一些困惑和难题,这样既能让学生深刻理解高数中难懂的概念、知识点,省去一些繁杂的计算过程,同时也引导学生学习一款实用软件,练习了编程技巧,提高利用所学抽象知识分析解决实际问题的能力。
本文将结合以下若干具体实例,阐述如何在高等数学教学过程中巧妙地融入Matlab软件使用,利用软件的图形显示和数据演算,将高等数学中一些概念的细微特点展示出来,利用Matlab软件强大的符号计算功能,将一些烦琐而又程序化的计算过程进行简化,节省计算时间,把更多的精力转移到对概念、方法、思想的学习和掌握中来,从而引导学生进行探索式学习[2,3,4]。
1 Matlab软件融入无穷小量概念的教学过程
无穷小量是一个抽象的概念,严格的数学定义是:在自变量某一变化过程中,以0为极限的变量或者函数[5]。教师在教授过程中往往会举出很多例子来加以阐述,但是仍有很多学生对概念理解不够深刻,从而导致在使用过程中,经常发生错误,比如,在做分式计算时为何0不能作分母而有时无穷小可以,无穷小量与有界量的乘积还是无穷小量,又如,无限多个无穷小不一定是无穷小,很多学生只是简单记住定义和结论,但在理解上依然存在困扰。因此,我们结合Matlab软件的图形可视化功能,将这个抽象概念转化为具体实例给学生展现其特征。
案例1 编写Matlab程序,观察当[x→+∞]时,函数[f(x)=1x]趋于0的极限过程。
Matlab程序如下:
clear
x=10:100:10000
n=length(x)
for i=1:n
f(i)=1/x(i);
end
plot(x,f)
axis([0 10000 -0.1 0.1])
title('无穷小量趋势图')
还可以利用软件,计算并列出一些数据进行对比观察,让学生增加直观印象,如下表1是当[x]取值较大时对应函数[f(x)]取值的几组数据:
从上述图1和表1的结果中,引导学生观察无穷小量只是一个随着自变量的变化趋势而无限接近0的动态量,而不是永远等于0的量,这就把无穷小和一個很小的量的本质区别很清晰地对比出来了。
案例2 观察当[x→+∞]时,无穷小量[1x]与有界量[sinx]的乘积[sinxx]的变化趋势。
Matlab程序如下:
clear
x=0:40:10000
n=length(x)
for i=1:n
f(i)=sin(x(i))/x(i);
end
plot(x,f)
axis([0 10000 -0.08 0.08])
title('无穷小量乘以有界量的趋势图')
以下表2是当[x]取值很大时,列举出的函数[sinxx]的对应几组数据:
从上述图2和表2的结果中,引导学生观察无穷小量乘以一个有界量是一个从0的左右两边无限趋近0的一个过程量,所以该乘积在自变量的这种趋势下也是无穷小量。
2 MAtlab软件融入积分定义的教学过程
一元函数积分学在高等数学甚至整个分析数学中具有重要的地位,准确深刻地理解定积分的定义能够对后续学习重积分、曲线积分和曲面积分,或者勒贝格积分、黎曼-斯蒂尔斯积分等打下坚实的基础。
2.1 Matlab软件融入到不定积分教学过程
从高等数学教材中知道,函数的不定积分是一族导数相同的函数集,在教学过程中会发现,对一些函数求不定积分时,利用不同的积分方法将会出现不同表达式的结果,虽然在课堂中教师都会给学生解释它们之间相差一个常数,但是有一大部分学生依然存在疑惑。为了帮助学生消除疑虑,我们可以利用Matlab软件对某一函数不定积分的不同解析表达式进行数值表示,并且用图形来进行对比。
案例3 利用不同方法,计算不定积分[1cosxdx]。
在文献[6]中,对于本题,通过不同的计算方法得到两个完全不同的表达式,分别为[ln(sec(x)+tan(x))+C]和[12ln1+sin(x)1-sin(x)+C],根据不定积分的定义,我们知道这两个解都是正解,而其中[ln(sec(x)+tan(x))]和[12ln1+sin(x)1-sin(x)]或者相等或者相差一个常数。具体如何,接下来,利用Matlab软件画图来进一步验证。
Matlab程序如下:
clc
clear
x=0:pi/100:pi/2-1
f1=log(1+sin(x))-log(cos(x));
f2=0.5*(log(1+sin(x))-log(1-sin(x)));
plot(x,f1,'-*',x,f2)
legend('ln(sec(x)+tan(x))','1/2(ln(1+sin(x))-ln(1-sin(x)))')
从图3中对两个函数曲线进行对比,可以看出这两个表达式其实是相同的函数。
2.2 Matlab软件融入到定积分教学过程
教材中对于定积分的定义篇幅较长,叙述复杂,共包含分割、近似计算、求和,、取极限四个部分,复杂的公式推导和证明往往让学生不能很好地理解相应的思想。我们通过结合Matlab软件将定义证明的几个部分编写成相关的算法,引导学生自主分析算法的特点,并且以相应数据和图像清晰感受到是如何进行分割,近似计算,求和,取极限,最后得到定积分的计算结果。这能够帮助学生摆脱繁杂的公式推导,简易地理解概念,也让学生在这个过程提高学习的热情和成就感。
案例4 设函数为[f(x)=1x],利用定义计算定积分[25f(x)dx][7]。
Matlab程序(利用矩形公式进行求解):
clear
a = 2;b = 5;N = 1000;
h = (b-a)/N; %分割区间[a,b]
x = a:h:b; %每个节点的自变量取值
f = @(x)1./x; %被积函数
y=x;
for i = 2 : N+1
y(i) = f((x(i)+x(i-1))/2); %利用两个节点中的中点对应的函数值来近似计算。
end
f1 = h * sum(y(1:end)) %求和和取極限过程
f2 = log(5)-log(2) %标准正确值
error = abs(f1-f2) %误差
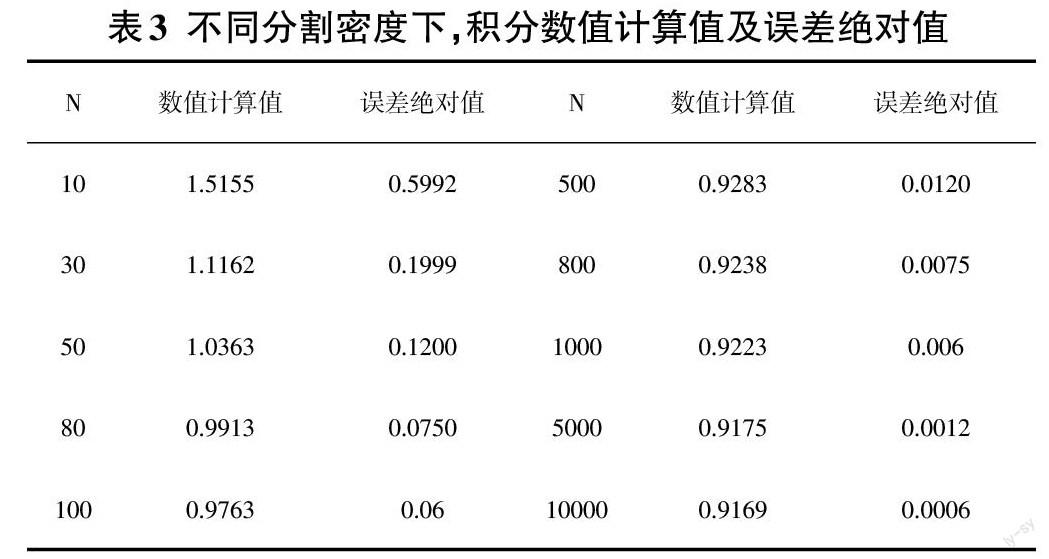
这里可以得到[25f(x)dx]标准结果为0.9163,当N取10000时,数值结果为0.9169。可以说明数值结果还是相当准确。
进一步通过让学生对上述程序的N进行修改,并观察误差的变化情况。从而去理解定积分算法中为什么要求[limλ→0](这里的[λ=max0 可以进一步利用软件,给出下表列出几组数据: 并且可以通过Matlab软件的画图功能,以曲线的形式来更加形象展示出定积分的极限过程,结果见图4。 Matlab软件画图程序如下: clear N=[10 30 50 80 100 500 800 1000 5000 10000]; f=[1.5155 1.1162 1.0363 0.9913 0.9763 0.9283 0.9238 0.9223 0.9175 0.9169]; f_exact = 0.9163*ones(size(f)); error = [0.5992 0.1999 0.1200 0.0750 0.06 0.0120 0.0075 0.006 0.0012 0.0006]; subplot(1,2,1) plot(N,f,'--bo') hold on plot(N,f_exact,'r') axis([0 10000 0.5 2]) legend('数值结果','精确结果') title('数值结果与精确结果对比图') subplot(1,2,2) plot(N,error,'-*') axis([0 10000 -0.2 0.7]) legend('误差') title('误差结果图') 3 Matlab软件融入P级数的教学 P级数是级数中一类较为特殊级数,学生一般只是通过老师在上课中的理论证明其收敛,在教学过程,学生往往会认为级数的[limn→∞an=0]是收敛的,对于其中的P级数的不收敛情况很多学生是存在疑惑的。对于这个疑惑我们用理论很难给学生一个直观的解释,所以可以利用Matlab软件,让学生清晰看到其结果,让学生理论结合实践更清晰去认识P级数敛散性。 案例5 讨论P级数[n=1∞1np=1+12p+13p+…+1np+…]的敛散性,其中[p>0]为常数[8]。 Matlab程序: p1 = symsum(1/n,n,1,inf); %当p=1时,即为调和级数 p2 = double(symsum(1/n^(1.2),n,1,inf)); %当p=1.2时,P级数的结果 p3 = symsum(1/n^2,n,1,inf); %当p=2时,P级数的结果 %% 下面分别为p=0.3,p=0.6,p=0.9,p=2的P级数图像对比 k1=0.3; k2=0.6; k3=0.9; k4=2 sum1=[]; sum2=[]; sum3=[]; sum4=[]; sum5=[]; for m=10:1000:100010 for i=1:m b1(i)=1/i^(k1); sumb1=sum(b1); b2(i)=1/i^(k2); sumb2=sum(b2); b3(i)=1/i^(k3); sumb3=sum(b3); b4(i)=1/i^(k4); sumb4=sum(b4); end sum1=[sum1,sumb1]; sum2=[sum2,sumb2]; sum3=[sum3,sumb3]; sum4=[sum4,sumb4]; end p03=sum1; p06=sum2; p09=sum3; p2=sum4; m=10:1000:100010; subplot(2,2,1); plot(m,p03); title('p=0.3') subplot(2,2,2); plot(m,p06); title('p=0.6') subplot(2,2,3); plot(m,p09); title('p=0.9') subplot(2,2,4); plot(m,p2);title('p=2') 程序输出结果: p1 = Inf p2 = 5.591582441177751 p3 = pi^2/6 從上述的结果可以具体得到,当P级数的[p>1]时为收敛的,当[p=1]时,得到的结果为Inf(表示无穷大),所以调和级数是发散的。同时从图5中我们也可以看到,当[p<1]时,级数和随着n变大而变大,说明其敛散性是发散的。而当[p=2]时,n达到一定大时,其和将保持不变,这也说明其敛散性是收敛的。 4 Matlab的可视化功能融入三重积分计算 三重积分的计算是高等数学中的一个难点问题,首先由于三维的积分区域很难具体地以图形的形式给出,所以学生在确定积分区域存在困难,其次计算过程相对复杂,容易出错,要求对定积分的方法掌握比较扎实。而Matlab软件可以较为容易画出相应的积分区域,可以准确用具体的图像表现出来,让学生清晰看到三重积分的积分区间,这样使得计算三重积分变得简单易理解。 案例6 计算三重积分[Ωzdv],其中积分区域[Ω]是由圆锥面[z=x2+y2]和圆柱面[x-12+y2=1]与平面[z=0]所围成的闭区域[9]。 分析:我们可以通过以下程序清晰的给出上述的积分区间图形,让学生具体形象的看到三重积分的积分区域。 Matlab程序: clear x = 0:0.1:2; y = -1:0.1:1; [x,y] = meshgrid(x,y); z_1 = sqrt(x.^2+y.^2); t=linspace(0,2*pi,length(x)); x1=sin(t)+1;y1=cos(t); z1=linspace(0,2.1,length(z_1)); X=meshgrid(x1); Y=meshgrid(y1); Z=[meshgrid(z1)]'; surf(x,y,z_1);%锥面上半部分 hold on; z_0=zeros(size(z_1)); surf(x,y,z_0);%锥面下半部分 hold on; mesh(X,Y,Z)%圆柱面 text(1,-1,1,'\leftarrow 柱面','Color','red','FontSize',18) text(1,0,1.9,'\leftarrow 锥面','Color','red','FontSize',18) xlabel('x'); ylabel('y'); zlabel('z'); axis equal 易知,图6所确定的积分区域 [Ω=r,θ,z0≤z≤r,0≤r≤2cos(θ),-π2≤z≤π2],所以,该三重积分可以写为[Ωzdv=Ωzrdrdθdz=-π2π2dθ02cosθrdr0rzdz=3π4]。 5 结语 在高等数学的传统课堂教学中,存在很多理论证明和公式推导,这使其课堂教学过程变得枯燥,同时也额外增加了概念知识的抽象性,学生常常难以理解,而对于非数学专业学生而言,复杂抽象的理论证明和推导并不是主要内容,更为客观的教学目标是让学生准确理解概念的内在含义,掌握典型的计算方法,学习精巧的数学思想,并且能够利用数学知识解决专业问题和实际问题的能力。通过充分利用当代先进的教学条件,在高等数学课堂中融入Matlab软件,就能够弥补传统教学中存在的这些不足,由此提高学生对高等数学的兴趣和热情,调动学生的学习主动性和积极性,另一方面,也使学生能够熟悉Matlab的使用规则,掌握一款实用性的工具软件,相信这对高等数学课堂教学质量和提高课程的实际应用效果具有重要的实践意义。 参考文献: [1] 刘卫国.MATLAB程序设计与应用[M].3版.北京:高等教育出版社,2017. [2] 杨然.Matlab符号计算在高等数学实验教学中的应用[J].现代职业教育,2019(28):202-203. [3] 李永芳.基于MATLAB软件的高等数学实验教学[J].高教学刊,2017(6):79-80. [4] 兀松贤.基于MATLAB的高等数学可视化辅助教学[J].喀什大学学报,2016,37(6):52-54. [5] 吴克义,兰德新.高等数学(上册)[M].北京:北京邮电大学出版社,2021. [6] 同济大学数学系.高等数学附册学习辅导与习题选解:同济·第七版[M].北京:高等教育出版社,2014. [7] 刘二根,王广超,朱旭生.MATLAB与数学实验[M].北京:国防工业出版社,2014. [8] 姜景连,吴克义,兰德新.高等数学(下册)[M].北京:北京邮电大学出版社,2021. [9] 吴赣昌.微积分:经管类 简明版[M].2版.北京:中国人民大学出版社,2008. 【通联编辑:梁书】
