求解PageRank 的修正多步幂-多分裂内外迭代法

罗 慧，马昌凤2

（福建师范大学数学与统计学院，福建，福州 350117）

0 引言

随着互联网及其技术的蓬勃发展,网络搜索引擎已经成为检索信息最受欢迎的工具。作为Google的关键技术PageRank 算法在过去十几年中一直受到科学界学者的关注。简而言之PageRank 问题可看作Google 矩阵首特征值1 所对应特征向量的求解。

Google 矩阵的定义如下：

为解决PageRank 问题，幂法是易于计算的且最经典的算法，但当阻尼因子α接近1 时，幂法收敛速度非常慢。为了改进幂法，Gleich 等[1]利用Richardson 迭代法提出了内外迭代法。Gu 等人将幂法和内外迭代法相结合，在文献[2]里提出了两步分裂迭代PIO 算法。随后，Gu 等人将多步幂法与内外迭代相结合，在文献[3]中开发了PIO 迭代的一种变体,也就是MPIO 方法，最近Pu 等人在文献[4]中介绍了一种基于多步幂法和多步分裂的IO 迭代的变体，用MPMIO 来表示。在以上文献的基础上，本研究提出了IO（PIO）迭代的一种变式，将多步幂法和多步分裂的IO 迭代的结合扩展到更为一般的情形，以加速PageRank 的计算。

1 内外迭代法

2 修正多步幂-多分裂内外迭代法（GPTI）

3 GPTI 算法的全局收敛性分析

本节我们主要分析所提出的算法在没有任何阻尼因子和停止误差下的全局收敛性情况。

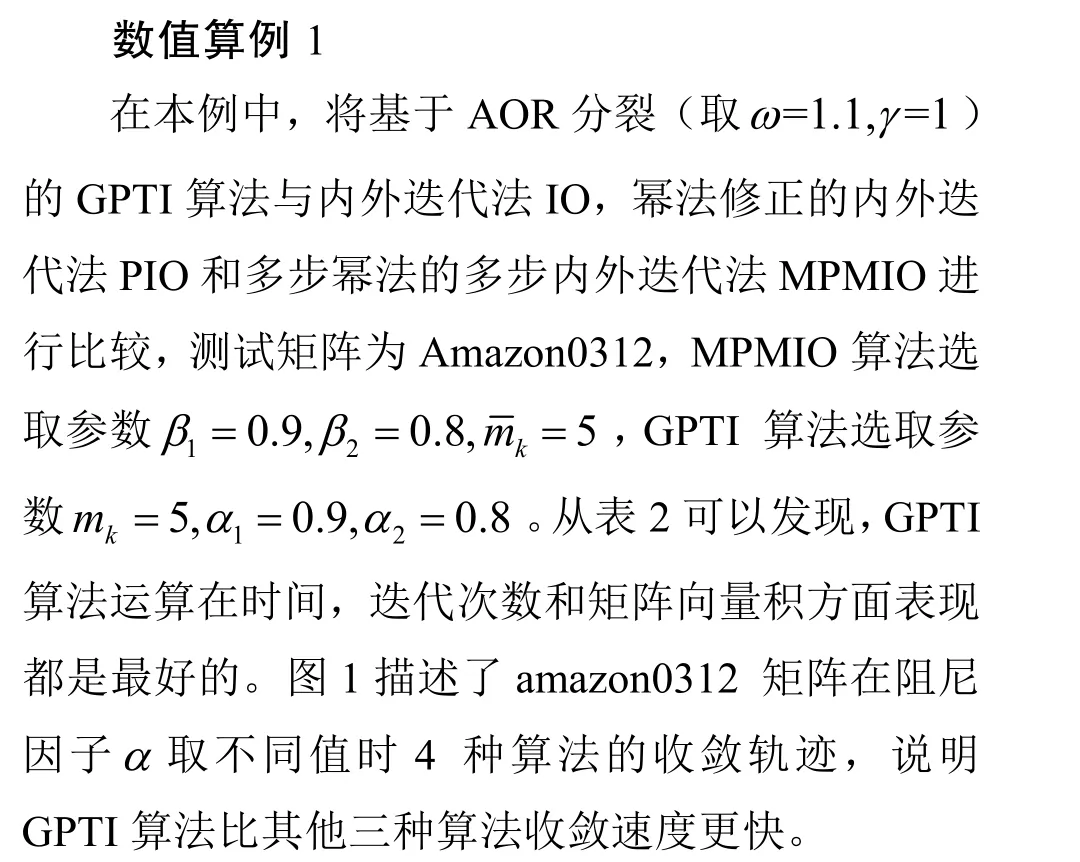
4 数值实验

表1 测试矩阵的性质Table 1 Properties of the test matrix

数值算例2

在本例中，将算例1 中矩阵换为维数更大，稠密度更小的测试矩阵Wiki-Talk，运算结果如表3 与算例1 类似。图2 描述了Wiki-Talk 矩阵在阻尼因子α取不同值时4 种算法的收敛轨迹，也说明GPTI 算法比其他三种算法收敛速度更快。

图1 Amazon0312 矩阵的测试结果Fig.1 Amazon0312 矩阵的测试结果

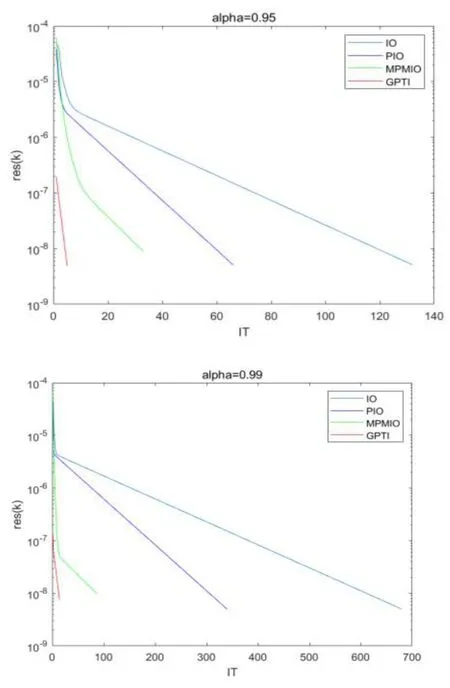
图2 Wiki-Talk 矩阵四种算法的收敛效果Fig.2 Wiki-Talk test results for the matrix

表2 Amazon0312 矩阵的测试结果Table 2 Test results for the Amazon 0312 matrix

表3 Wiki-Talk 矩阵的测试结果Table 3 Test results for the Wiki-Talk matrix