基于FPGA的数字图像几何畸变矫正方法研究
2022-08-31刘婧
刘 婧
(山西旅游职业学院 电教中心,山西 太原 030036)
1 引言
现阶段,通常将图像作为载体进行处理和分析[1-2]。除了传统的工业以及科研领域外,传统的胶片相机已经被数码相机所取代,同时具有摄像功能的电子设备越来越多,图像处理技术被广泛应用于各个领域中。现阶段,图像处理方法针对正常图像的处理效果较好,但是由于畸变图像往往存在一定的几何误差,影响图像处理效果,因此,对数字图像几何畸变进行矫正成为当前研究的热点话题。
陈文艺[3]等人提出一种基于深度学习的单张图像畸变校正方法,该方法首先构建图像序列,并对相机参数进行估计,然后对图像径向畸变参数之间的函数关系进行分析,最后采用深度学习方法实现图像畸变校正。廖书红[4]等人主要对数字图像进行交叉以及存储等操作,同时结合DDR3优化存储方案进行畸变图像校正。以上两种方法虽然取得了较为显著的研究成果,但是由于未能对数字图像进行去噪处理,导致校正误差、复杂度和时间增加。为此,提出基于FPGA的数字图像几何畸变矫正方法,该方法的矫正误差较低、矫正时间较短,且降低了图像处理的复杂度。
2 数字图像几何畸变矫正方法
2.1 基于FPGA的数字图像去噪处理
为了获取更加理想的矫正效果,需要优先对数字图像进行降噪处理。如果利用降级过程可以将其从原始的“真”信号转换为原始信号X,从而获取观测信号I,其表达式为:

进行滤波的主要目的是在观测信号中有效恢复原始信号X。在双边滤波中主要包含特定形式的局部滤波,也就是将其转换为最小化问题[5-6],具体的表达式如下:
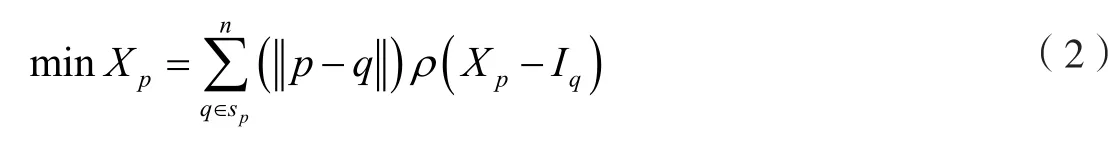
上式中,p和q代表像素;sp代表像素p的邻域;Xp代表需要求解像素p的灰度值;代表p和q两点之间的欧几里得距离。
对公式(2)进行求导,即:

设定δ(x) =ψ(x) /x,将其代入公式(3)中,则能够获取如下的计算式:
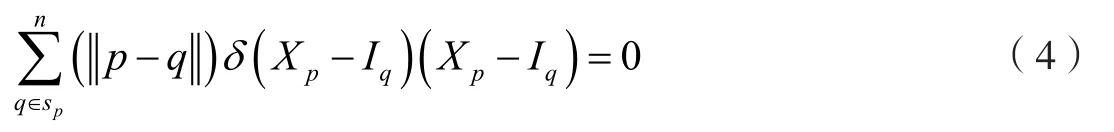
将公式(4)进行化简,则能够获取以下的形式:
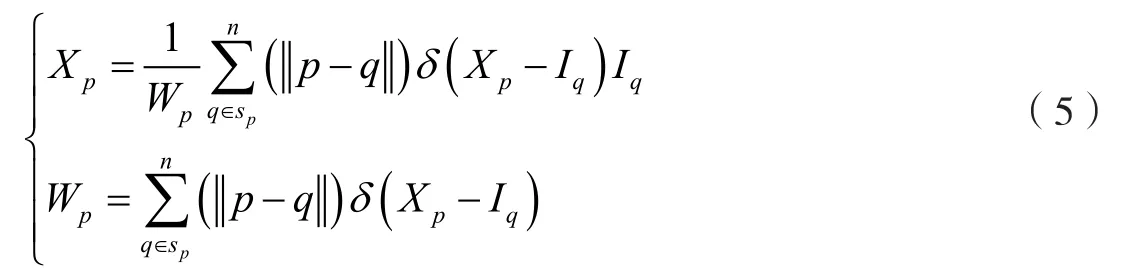
公式(5)代表局部滤波模式进行滤波的滤波式。假设h(x)和δ(x)代表高斯函数,则公式(5)能够通过以下的形式表示:

上式中,sσ代表标准方差;rσ代表标准偏差。通过sσ和rσ能够分别决定空间核函数的值域以及函数的展开程度[7]。为了有效求解公式(6),需要将公式(6)进行重写,具体的计算式为:

经过多次验证发现,当高斯滤波器σs=1时,且双边滤波器满足以下约束条件时,能够获取较高的峰值信噪比,实现数据图像去噪:

上式中,nσ代表高斯滤波函数。
2.2 数字图像几何畸变矫正
对图像进一步进行自动阈值分割处理,通过分割得到二值图像,其中二值图像是由背景和明显区域两个部分组成;当数字图像经过分割后,采用形态边界检测方法对数字图像的边界部分进行存储和记录,并且利用Radon变换对数字图像中较为明显的轮廓进行提取;进而计算数字图像各个顶点位置的坐标以及横纵比,同时判定图像是否需要进行旋转,最终实现矫正。图1为具体的操作流程。
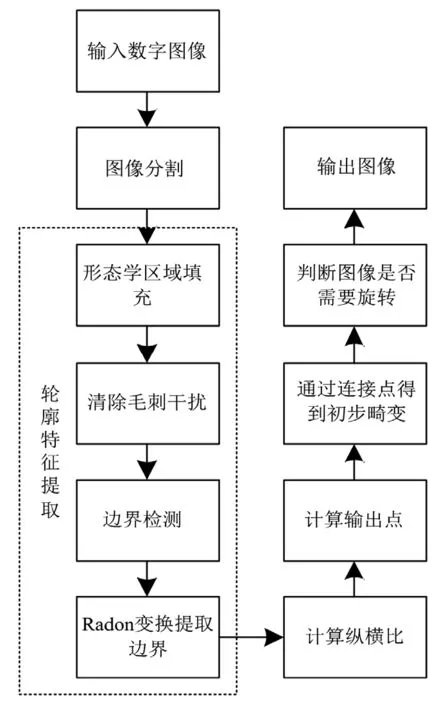
图1 基于FPGA的数字图像几何畸变矫正流程
图像处理过程中十分关键的步骤就是图像分割,它是一种基础的计算机视觉技术,本文采用Otsu算法对数字图像进行分割操作[8-9]。
设定L表示初始灰度图像的灰度级,则数字图像内的全部像素可以表示为:

归一化直方图,则能够获取以下的计算式:

上式中,pi代表期望图像像素点。
通过阈值t划分灰度值,则通过公式(11)表示C1和C2类出现的概率和均值:
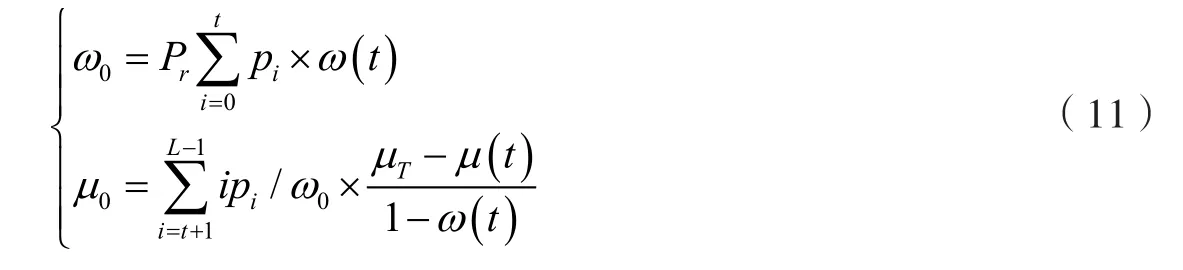
将C1和C2两个类获取最佳分离的阈值t设定为最佳阈值,具体的表达形式如下:

上式中,η(t)代表图像二值化阈值。
通过形态学的填充区域算法对经过阈值分割后的图像进行区域填充,即:

上式中,Xk代表填充结果;Ac代表待填充区域集合。
在获取的二值图像中,背景上面还存在白色的毛刺,毛刺的存在会影响最终的数字图像几何校正结果[10]。为此,需要及时清理毛刺。使用形态学开操作对毛刺进行清除,同时还需要进行边界检测,设定集合A的边界为β(A),其能够利用B对A进行腐蚀操作,然后通过A减去腐蚀获取毛刺清理结果,具体的计算式为:

其中,通过Radon变换提取边界的具体操作流程如下所示:
(1)对全部的边界图像进行Radon变换;
(2)在Radon变换图像上获取一个亮点极值坐标,设定各个亮点的取值为0;
(3)重复步骤(2)的操作,直至获取4个亮点的极值坐标;
(4)分别计算出四条不同边界的直线坐标。
横纵比主要是指矩形的宽度和长度之比,在数字图像中,图像的横纵比发生变化,图像即会发生变形,同时图像上的符号也开始失真。
数字图像的畸变校正过程需要输入的点十分容易选择,即数字图像的四个顶点。对应输出点的坐标就是通过输入点坐标以及相对的几何关系进行纵横比计算[11],以下给出具体的操作步骤:
(1)将数字图像的左下角设定为第一输入点,同时确保其他输入点坐标保持不变,具体的表达式为:

上式中,(x01,y01)代表第一输入点坐标。
(2)将数字图像右下角的输入点作为第二输入点,则对应输出点行坐标和第一输出点的行坐标相同:

上式中,d代表输入点之间的距离。
(3)将左上角的输入点作为第三输入点,设定λ代表纵横比,具体的计算式为:

(4)右上角的输入点设定为第四输入点,对应输出点的坐标能够表示为:

分析坐标转换公式,能够获取旋转后数字图像的四个顶点坐标,如下所示:
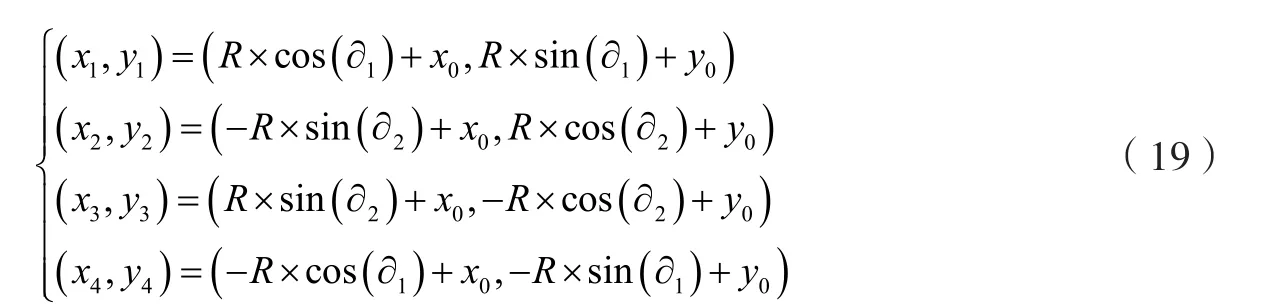
上式中,R代表旋转中心点;∂1代表坐标点平移;∂2代表坐标点旋转。
在上述分析的基础上,通过输入点和对应输出点的坐标对数字图像进行几何畸变初步矫正,但是为了获取更加清晰的图像,还需要对数字图像进行归一化操作以及旋转判断[12],具体的操作流程如下:
(1)优先采用Ostu对数字图像进行自动阈值分割,同时将数字图像进行字符分割。
(2)采用形态学切割数字图像中需要识别的文字,在二值数字图像中检测获取第一个黑色像素点,如果它是连通区域内的一个黑色像素点,则将其设定为递归的开始,接着进行连续膨胀,直至获取连通区域内全部的像素点。
(3)针对全部数字图像的分割结果进行归一化操作。
(4)通过数字特征对图像中的数字进行识别,判断数字图像是否需要进行旋转,最终实现数字图像几何畸变矫正。
3 仿真实验
为了验证所提基于FPGA的数字图像几何畸变矫正方法的综合有效性,在Windows10系统,Intel Corei7-9700处理器,4GB内存的硬件环境下进行实验分析。将图像矫正复杂度和矫正时间等指标作为实验指标,对比文献[3]方法、文献[4]方法和所提方法的图像处理效果。分别选取100幅数字图像作为测试对象,其中,包含风景、人物、建筑等多种类型,为了保证实验结果的一致性,实验中所产生的数据均由Matlab软件进行处理。
3.1 数字图像几何畸变矫正误差/(%)
对比三种不同方法的数字图像几何畸变矫正误差,具体的实验对比结果如图2所示。
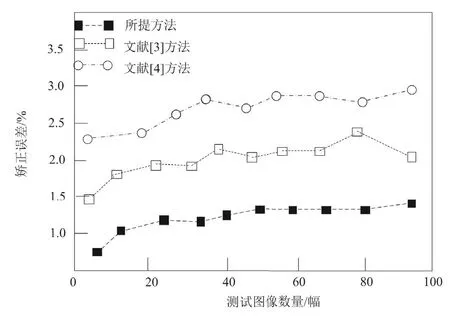
图2 数字图像几何畸变矫正误差对比结果
分析图2中的实验数据可知,所提方法的矫正误差始终低于1.5%,而文献[4]方法的矫正误差最大值接近3.0%,说明所提方法经过去噪后,获取的图像更加适合信息读取,同时校正结果也十分令人满意。但是由于另外两种方法在实际操作的过程中,并没有对数字图像进行去噪操作,致使整个方法的数字图像几何畸变矫正误差较大,数字图像几何畸变矫正误差明显高于所提方法。
3.2 数字图像几何畸变矫正复杂度/(%)
由于各个方法的操作流程存在十分明显的差异,致使整个方法的校正复杂度也存在十分明显的差异,通过数值对复杂度进行表示,数值越小,复杂度越低,利用表1给出详细的实验对比结果:
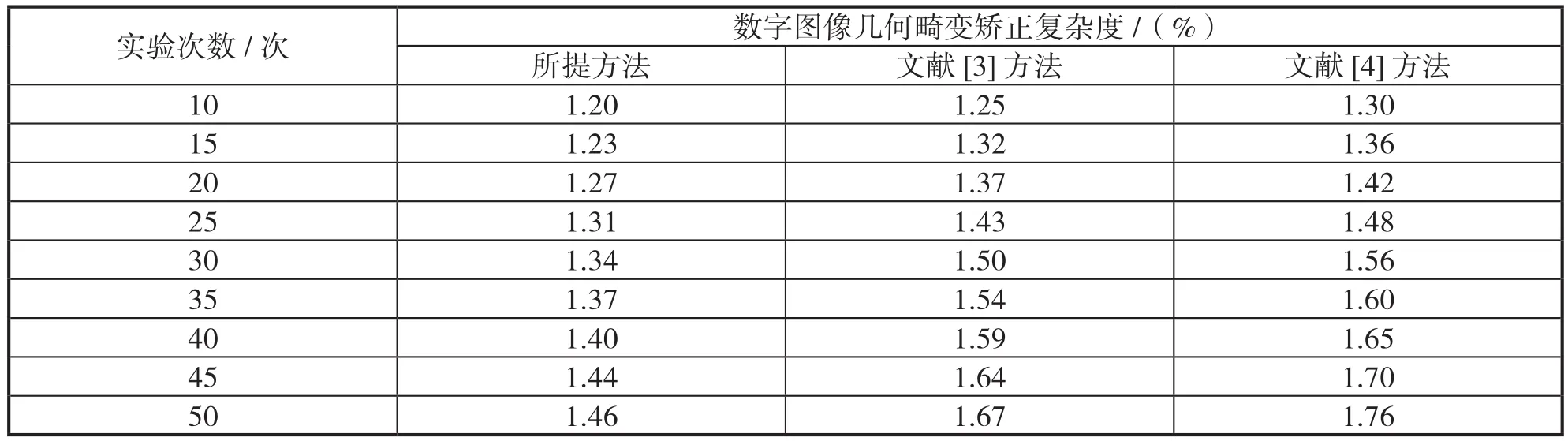
表1 数字图像几何畸变矫正复杂度对比结果
分析表1中的实验数据可知,由于所提方法简化了图像矫正流程,有效降低了数字图像几何畸变矫正复杂度。因此,在三种方法中,所提方法的数字图像几何畸变矫正复杂度明显更低。
3.3 数字图像几何畸变矫正时间/(min)
利用图3给出不同方法的数字图像几何畸变矫正时间对比结果
根据图3可知,所提方法的数字图像几何畸变矫正时间最短;文献[3]方法和文献[4]方法在图像数量低于90幅时,矫正时间差距不明显,但是之后文献[3]方法的矫正时间增长明显。通过对比证明,对数字图像进行去噪具有一定的可行性,有效降低了图像矫正时间。
4 结束语
针对传统图像几何畸变矫正方法存在的矫正效果不佳的问题,研究基于FPGA的数字图像几何畸变矫正方法。通过实验结果可知,所提方法能够有效降低数字图像几何畸变矫正误差和复杂度,同时还能够较少矫正时间。但是由于受到环境以及人为等多方面因素的限制,致使所提方法仍然存在一定的不足,需要加强完善。
