基于相场法的裂缝性地层压裂裂缝延伸特征研究
2022-08-31易良平杨若愚肖佳林李小刚杨兆中
易良平,张 丹,杨若愚,肖佳林,李小刚,杨兆中
(1.西南石油大学机电工程学院,四川成都610500;2.西南石油大学油气藏地质与开发国家重点实验室,四川成都610500;3.中国石油西南油气田勘探事业部,四川成都610041;4.中国石化江汉油田分公司工程技术研究院,湖北武汉430035)
水力压裂是低渗与致密储层商业化开发的关键技术[1-2]。对于孔隙型储层,水力裂缝形态较为单一,但在页岩、煤岩和其他具有天然裂缝的地层中,水力裂缝形态为复杂的裂缝网络。部分研究表明,水力裂缝沟通天然裂缝有利于低渗储层的经济开发[3-4]。然而,实验研究表明,当水力裂缝与天然裂缝相交时,可能发生穿过天然裂缝、沿天然裂缝扩展或被天然裂缝捕获等现象[5]。
近年来,虽然室内物理实验[5-9]直观地呈现了天然裂缝影响下的水力裂缝的延伸特征,但由于室内物理实验装置尺寸的限制,难以直接观察到压裂裂缝延伸的动态过程,因此,部分研究者采用数值模拟手段仿真天然裂缝影响下水力裂缝延伸过程。
目前,用于研究水力裂缝和天然裂缝相交的数值模拟方法主要包括:位移不连续性方法[10-13]、离散元方法[14-15]、黏聚单元法[16-18]、扩展有限元法[19-21]。近年来,基于相场法(PFM)建立的水力裂缝延伸模型引起了研究人员的关注,在该理论框架中网格边界不需要和裂缝边界重合,因此,裂缝延伸后不需要重新剖分网格。该方法可以灵活地处理多物理场作用下裂缝的萌生、演化、汇集和延伸[22-24]。
PFM是根据变分法原理建立的[25-30],该方法使用连续扩散的相场变量c来描述裂缝,c的变化范围在0和1 之间,当c等于0 或1 时,分别代表岩石完好无损和完全破裂(图1)[31]。
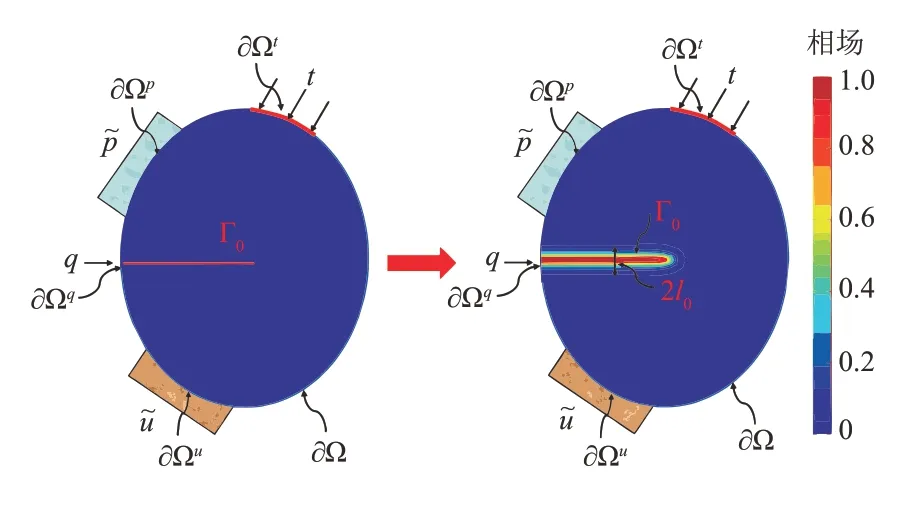
图1 相场法示意图[31]Fig.1 Schematic of phase-field method[31]
现有基于相场法建立的多孔弹性介质中压裂裂缝延伸模型[22-24]的共同特征是:①需要通过计算裂缝宽度来计算水力裂缝渗透率,因此,需要通过额外的规则来追踪裂缝界面;②将天然裂缝的相场初始值设置为1(即天然裂缝处于未胶结状态)。
在现有研究基础之上,基于PFM 建立了一套新的多孔弹性介质中水力裂缝扩展模型,模型的创新之处在于:①流体流动遵循达西定律,岩石的渗透率是各向异性的,且是最大主应变的函数,因此,不需要计算裂缝宽度;②由于地下天然裂缝通常是胶结的,因此,研究中天然裂缝单元初始状态是无损伤状态,即天然裂缝单元的初始相场值为0。另外,基于建立的模型,进一步系统研究了原地应力差、水力裂缝与天然裂缝相交角、注入速率和压裂液黏度对水力裂缝延伸轨迹的影响。
1 数值模型
1.1 控制方程强形式
1.1.1 多孔弹性介质应力平衡方程
将地下岩石视为完全饱和的多孔介质,根据BIOT[32]提出的孔弹性力学理论,计算公式为:

式(1)—式(2)中:α为Biot系数;K为多孔介质体积模量,MPa;Ks为固体颗粒体积模量,MPa;σ为总应力,MPa;σeff为岩石骨架有效应力,MPa;p为孔隙流体压力,MPa。
水力压裂可看作准静态和小变形过程,因此,在忽略体力条件下,多孔弹性岩石的应力平衡方程可写为:
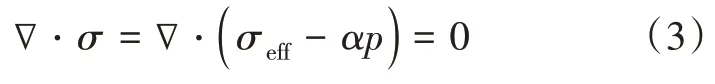
1.1.2 渗流控制方程
计算得到多孔介质的Biot 模量,再结合达西定律和BIOT 多孔弹性理论,可以得到多孔弹性介质中流体流动的连续性方程:

式(4)—式(5)中:M为多孔介质的Biot模量,Pa;Kf表示流体的体积模量,Pa;φ表示多孔介质的孔隙度;t为时间,s;μ为流体黏度,Pa·s;εii为体积应变。
式(5)中的k 为各向异性渗透率张量,二维条件下,k可表示为:
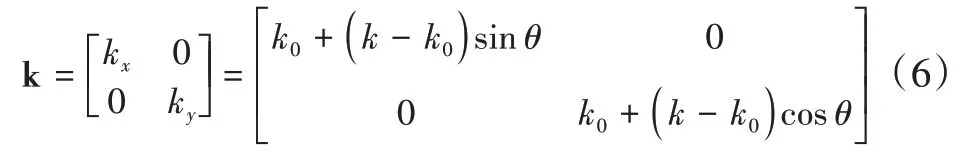
式中:kx、ky分别为x、y方向渗透率,m2;k0为岩石基质初始渗透率,m2;k为多孔介质渗透率,m2;其值取决于最大主应变ε1。
在本模型中,采用如下公式进行计算:

式(7)—式(8)中:θ为裂缝面法向方向角或最大主应变方向角,° ;b1、b2、b3为常数,需要通过实验数据拟合得到;γxy为切应变;εy为y方向的应变。
1.1.3 裂缝延伸相场演化模型
在水力压裂过程中,多孔介质的总自由能密度可分解为3部分:

式中:ψeff为储存于岩石骨架中的弹性应变能密度,Pa;ψfluid为储存于流体中的能量密度,Pa;ψfrac为形成新裂缝面耗散的能量密度,Pa。
由于损伤会降低岩石的刚度和拉伸能量[22-23],被破坏的岩石不具有与完整岩石相同的弹性应变能的存储能力。因此,将受损岩石的弹性应变能密度定义为[23]:
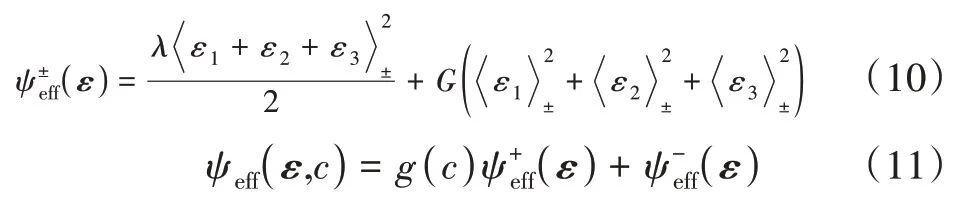
由式(11)可知,式(3)中的有效应力可写为:

储存于流体中的能量密度取决于流体体积分数增量ζ=p/M+αεii,并且必须满足以下条件:

因此,储存于流体中的能量密度可定义为[25]:

在相场法中,产生新裂纹而导致的能量耗散密度公式为:
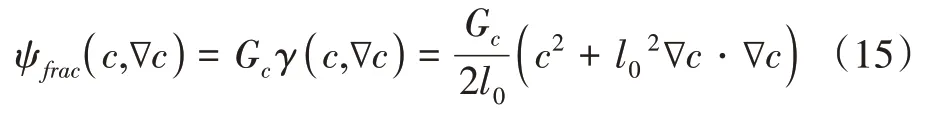
根据EMDADI等[33]的理论:

式(15)—式(16)中:Gc为Griffith 临界能量释放速率,J/m2;γ(c,∇c)为裂缝表面密度[23],J/m2;l0为长度尺度参数,m;E为岩石的弹性模量,Pa;σc为临界应力,Pa。
将式(11)、式(14)和式(15)代入式(9)可得总自由能密度ψ的表达式。在与速率无关的条件下,可通过Kuhn-Tucker方程[23-24]得到演化准则:

进而可通过ψ的变分导数确定裂缝相场演化方程,如式(18):
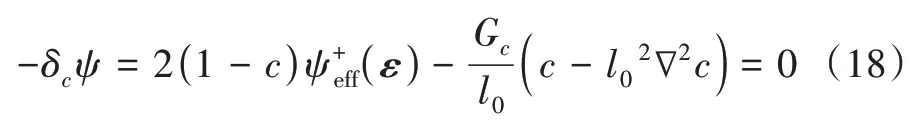
但由于岩石损伤为不可逆过程,因此,式(18)可改写为如下形式:

式(19)—式(20)中:H(x,t)为整个过程中应变能密度函数的最大值。
1.1.4 控制方程汇总及边界条件
基于相场法的多孔弹性介质中水力裂缝延伸控制方程组由以下3个偏微分方程组成:①应力平衡方程,如式(3);②多孔弹性介质中流体流动连续性方程,如式(4);③裂缝相场演化方程,如式(19)。对应的边界条件分别如式(21)—(23):
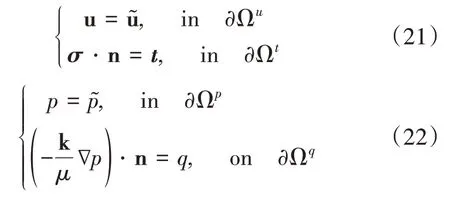

但式(21)—(23)中各边界需满足以下条件:
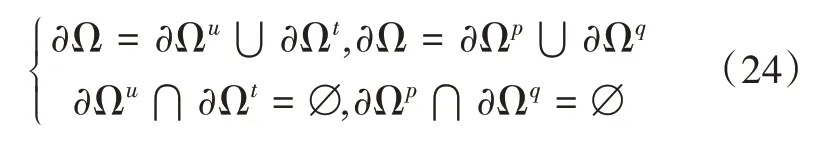
1.2 控制方程弱形式
控制方程式(3)、式(4)、式(19)分别乘以权函数wu、wp、wc,并在计算域Ω 上积分,再利用高斯散度定理,结合相应的边界条件,可得到控制方程的等效积分“弱”形式:

1.3 控制方程有限元离散
采用有限元方法离散控制方程的弱形式。每个单元的位移、压力、相场及其梯度的插值形式如下:
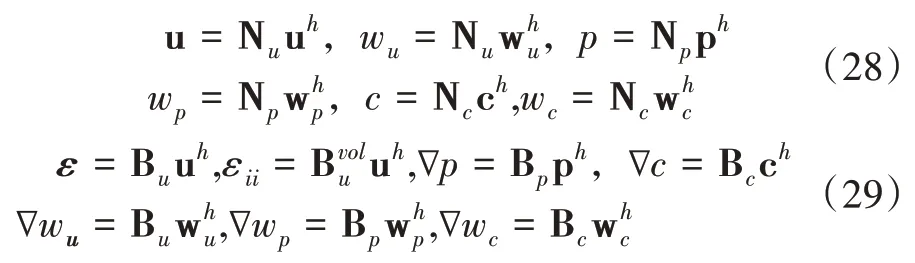
式(28)—式(29)中:uh,ph和ch分别表示单元节点上的位移、压力和裂缝相场;Nu,NP和Nc分别为位移、压力和裂缝相场的插值形函数,且均为四节点双线性函数;Bu,BP和Bc分别表示形函数的导数矩阵为体积应变矩阵。
将式(28)和式(29)代入式(25)—(27)中,并采用后向欧拉法离散公式式(26)中与时间有关的项,得到:

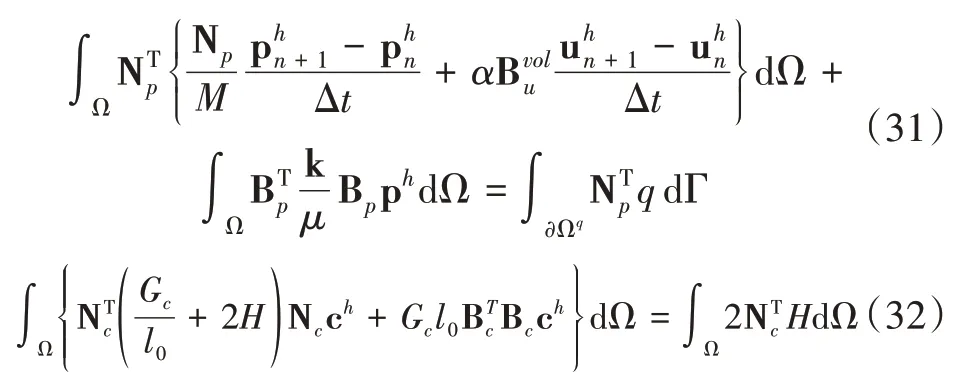
为了表达方便,将所有在第n+1个时间步未知量的下标删掉,则式(31)可改写为:

1.4 控制方程求解
控制方程式(30)、式(32)和式(33)相互耦合形成非线性方程组。为了方便求解,在每一个迭代步中先将裂缝相场值设为固定值,并采用Newton-Raphson(NR)迭代法求解渗流-应力耦合方程组式(30)和式(33),求得压力和位移后,再求解裂缝相场演化方程。则渗流-应力耦合方程组在第i个迭代步NR迭代格式可写为:

式(34)—式(40)中:Ru为应力方程的余量形式;Rp为渗流方程的余量形式;Juu、Jup、Jpu、Jpp为雅可比矩阵中的分项。
通过式(40)求得位移增量δuh和压力增量δPh后,第i+1个迭代步的位移和压力试探解可写为:

获得第i+1 个迭代步位移和压力试探解后,通过求解方程可得到裂缝相场值,在该过程中位移和压力值是固定的:

在每个时间步内,当位移、压力和裂缝相场都满足式(44)所示的收敛条件时,则迭代结束,进入下一时间步的计算,否则迭代继续进行:
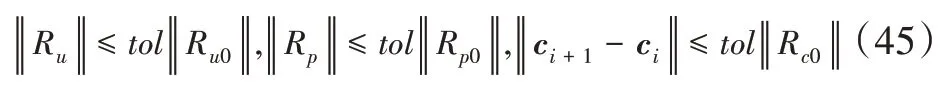
式中:tol为收敛容差,取值为1×10-5。
最后,优选MATLAB 软件编写相应数值计算程序求解上述数值计算模型。
2 数值算例
2.1 模型收敛性验证
为了验证模型的收敛性,模拟时间步长分别为2 s、1 s 和0.5 s 的裂缝扩展情况。模拟所采用的计算区域及边界条件如图2 所示,计算区域是边长为20 m的正方形,其中心有1 条长度为2 m 的初始裂缝。计算区域被均匀剖分为80×80 个正方形单元,左边界x方向的位移和下边界y方向的位移固定,分别对右边界和上边界施加25 MPa 和20 MPa 的压应力,初始孔隙流体压力为10 MPa。整个计算过程中,外边界流体压力保持为10 MPa,流体从注入点以0.003 m2/s 的速度注入,总注入时间为24 s,长度尺度参数l0设为0.5 m,其他输入参数见表1。

图2 模型收敛性分析算例中计算域和边界条件示意图Fig.2 Schematic of computational domain and boundary conditions for model convergence example

表1 模型收敛性分析算例中输入参数Table 1 Input data for convergence study example
由3 种不同时间步长算例中注入结束时裂缝相场云图和流体压力云图(图3、图4)可知,两者具有相同特征。具体表现为:①压裂裂缝沿最大水平应力方向(y方向)直线延伸;②由于压裂液滤失,裂缝周围流体压力略高于初始压力,但流体压力升高区域主要集中在裂缝区域。从3 种不同时间步长算例中注入点压力随时间的变化曲线可知,3条曲线几乎重合,由此可验证数值模型的收敛性(图5)。
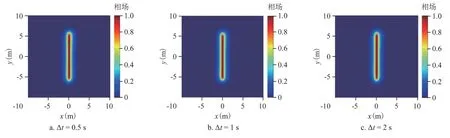
图3 3种不同时间步长情况下注入结束时裂缝相场分布Fig.3 Fracture phase field distribution contours at the end of injection under three different time steps

图4 3种不同时间步长情况下注入结束时流体压力分布Fig.4 Fluid pressure distribution contours at the end of injection under three different time steps
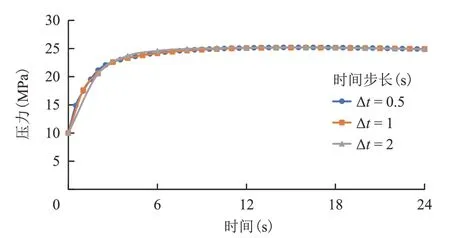
图5 3种不同时间步长情况下注入点压力随注入时间变化Fig.5 Pressure at injection point versus injection time with three different time steps
2.2 水力裂缝延伸轨迹影响因素分析
模拟分析影响水力裂缝延伸轨迹的几个关键因素。模型的计算区域为20 m×20 m 的正方形(图6),其中心有一条长为2 m的初始裂缝,流体从注入点注入,在距注入点3 m处存在与初始裂缝成一定相交角的天然裂缝,将该计算域均匀剖分为80×80个正方形单元,最大水平地应力和最小水平地应力分别作用于上边界和右边界,长度尺度参数l0设为0.5 m,其他输入参数见表2。
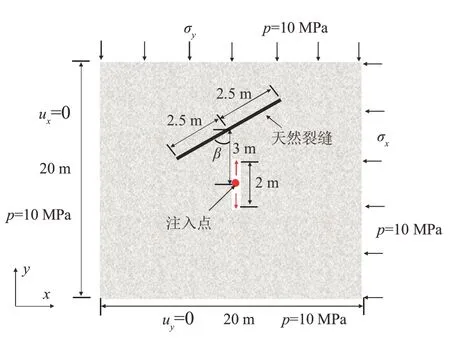
图6 影响因素分析算例所采用计算域和边界条件Fig.6 Schematic of computational domain and boundary conditions for influencing factors study

表2 影响水力裂缝延伸轨迹的模拟参数Table 2 Simulation parameters which affect hydraulic fracture extension trajectory
2.2.1 原地应力差和相交角的影响
将σx设为20 MPa,σy分别设为22.5 MPa、25 MPa和30 MPa,研究原地应力差(σy-σx)和相交角(β)对裂缝延伸轨迹的影响。
相交角为30°时,由3 种不同应力差下水力裂缝延伸情况可知:原地应力差为2.5 MPa和5 MPa时,水力裂缝与天然裂缝相交前沿直线扩展(图7a、图7d),随着流体继续注入,水力裂缝沿天然裂缝的右翼延伸(图7b、图7e),直到水力裂缝延伸到天然裂缝右翼尖端后再转向沿最大地应力方向(y方向)延伸(图7c、图7f)。当原地应力差增大到10 MPa时,水力裂缝将直线穿过天然裂缝,这种情况下水力裂缝无法激活天然裂缝(图7g,图7i)。

图7 相交角为30°时不同原地应力差条件下裂缝相场演化Fig.7 Fracture propagation processes for different in-situ stresses at an approach angle of 30°
相交角为45°时,由3 种不同应力差下水力裂缝延伸情况可知:相交角为45°时与相交角为30°时水力裂缝延伸特征具有相似性。即原地应力差为2.5 MPa和5 MPa时(图8a—图8f),水力裂缝沿天然裂缝右翼扩展,随后在天然裂缝右翼尖端沿y方向扩展。当原地应力差为10 MPa 时(图8g—图8i),天然裂缝不会影响水力裂缝的延伸轨迹,水力裂缝将直线穿过天然裂缝。
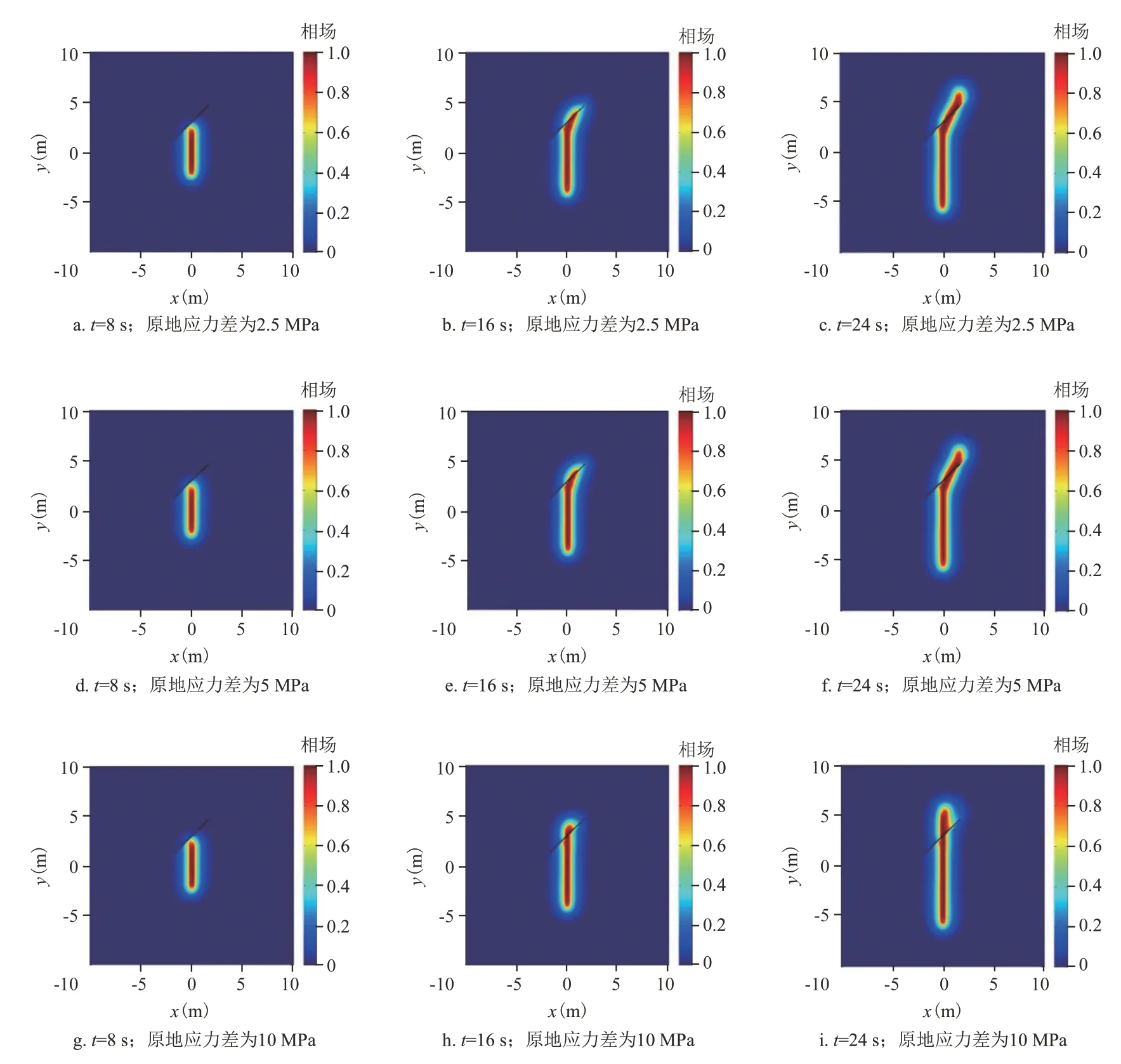
图8 相交角为45°时不同原地应力差下裂缝相场演化Fig.8 Fracture propagation processes for different in-situ stresses at an approach angle of 45°
相交角为60°时,由3 种不同应力差下水力裂缝延伸情况可知:原地应力差为2.5 MPa 和5 MPa 条件下水力裂缝延伸特征具有相似性(图9a—图9f)。具体表现为:水力裂缝与天然裂缝相交后将沿天然裂缝右翼延伸一定距离,然后再转向沿y方向延伸。但原地应力差为2.5 MPa 时,水力裂缝沿天然裂缝的延伸距离略大于应力差为5 MPa 时的延伸距离。当应力差进一步增加到10 MPa 时,水力裂缝将直线穿过天然裂缝(图9g—图9i)。

图9 相交角为60°时不同原地应力差下裂缝相场演化Fig.9 Fracture propagation processes for different in-situ stresses at an approach angle of 60°
综合分析上述模拟结果可知:相交角和原地应力差越小,天然裂缝越容易被水力裂缝开启(表3)。
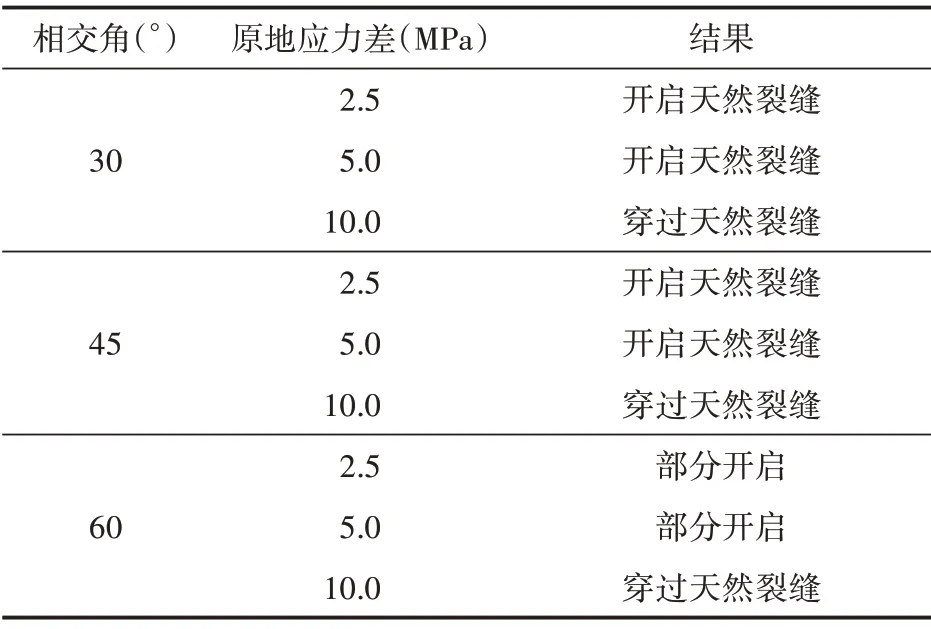
表3 水力裂缝与天然裂缝在不同相交角和原地应力差条件下的相交情况Table 3 Intersection behaviours of the hydraulic and natural fractures for different approach angles and in-situ stress differences
2.2.2 注入速率的影响
将相交角和原地应力差分别设置为45°和5 MPa,分别模拟注入速率为0.001 5 m2/s 和0.006 m2/s 时的裂缝延伸情况,再与注入速率为0.003 m2/s 时的裂缝延伸情况(图8d—图8f)进行对比。为了确保流体加载强度和总注入量相同,注入速率为0.001 5 m2/s算例中时间步长和注入时间分别设置为4 s 和48 s,注入速率为0.006 m2/s,算例中时间步长和注入时间分别设置为1 s 和12 s。即3 种注入速率条件下每个时间步的流体加载强度均为0.006 m2,总注入量均为0.072 m2,模拟输入的其他参数见表2。
综上所述,由注入速率为0.001 5 m2/s、0.006 m2/s时的裂缝相场演化(图10—图11)可知:3 个不同注入速率下裂缝延伸轨迹具有相似性,即水力裂缝将转向沿天然裂缝右翼扩展,但在这3种不同注入速率条件下,裂缝相场变化存在一定差异。在0.003 m2/s和0.006 m2/s 注入速率条件下,水力裂缝扩展到天然裂缝右翼最顶端后再转向沿y方向扩展;在0.001 5 m2/s的注入速率条件下,水力裂缝沿天然裂缝右翼延伸一定距离后(未到顶端)即转向沿y方向扩展。另外,由3种不同注入速率条件下注入点压力随注入量的变化关系可知(图12):3条曲线具有相同趋势,在初始阶段,注入点压力随注入量增加而增加,但较低的注入速率不利于完全开启天然裂缝,而过高的注入速率会导致注入压力较高,这对压裂施工管柱和地面设备的要求较高。因此,在压裂施工过程中,在井口装备和地下管柱强度允许的条件下应尽量提高施工排量。

图10 注入速率为0.001 5 m2/s时裂缝相场演化Fig.10 Snapshots of fracture phase-field evolution contours corresponding to injection rate of 0.001 5 m2/s

图11 注入速率为0.006 m2/s时裂缝相场演化Fig.11 Snapshots of fracture phase-field evolution contours corresponding to injection rate of 0.006 m2/s

图12 在3种不同注入速率下注入点压力与注入量关系Fig.12 Pressure at injection point versus injection volume for three different injection rates
2.2.3 压裂液黏度的影响
将相交角和原地应力差分别设置为45°和5 MPa,模拟压裂液黏度为3 mPa·s和5 mPa·s时的裂缝扩展情况,再与压裂液黏度为1 mPa·s时的裂缝扩展情况(图8d—图8f)进行对比,其他模拟输入参数见表2。
压裂液黏度为1 mPa·s、3 mPa·s 和5 mPa·s 时的裂缝相场分布(图8b、图13、图14)可知:3 种不同压裂液黏度条件下水力裂缝延伸特征具有相似性,水力裂缝沿天然裂缝右翼延伸,随后在天然裂缝右翼顶端再转向沿y方向扩展。但也有不同点,具体表现为随着压裂液黏度的增加,水力裂缝的长度略有减少。由3 种不同压裂液黏度条件下注入点压力随注入时间变化特征(图15)可知,注入压力随压裂液黏度的增加而增加。

图13 压裂液黏度为3 mPa·s时裂缝相场演化Fig.13 Snapshots of fracture phase-field evolution contours corresponding to fluid viscosity of 3 mPa·s
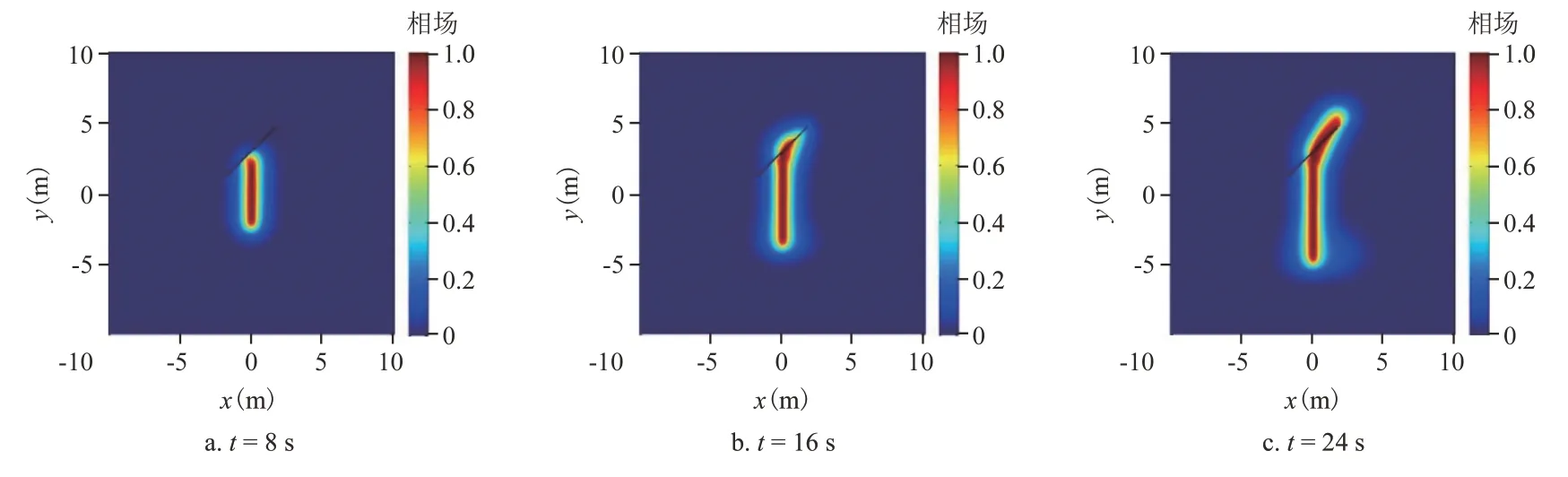
图14 压裂液黏度为5 mPa·s时裂缝相场演化Fig.14 Snapshots of fracture phase-field evolution contours corresponding to fluid viscosity of 5 mPa·s

图15 3种不同压裂液黏度下注入点压力与注入时间关系Fig.15 Pressure at the injection point versus the injection time for three different fluid viscosities
2.3 模型验证
对比研究模型的模拟结果(表3)与ZHOU[5]等物理模拟实验结果(图16)可知:虽然存在异常点,但模型模拟结果与实验结果吻合较好,进而验证了模型的可靠性。
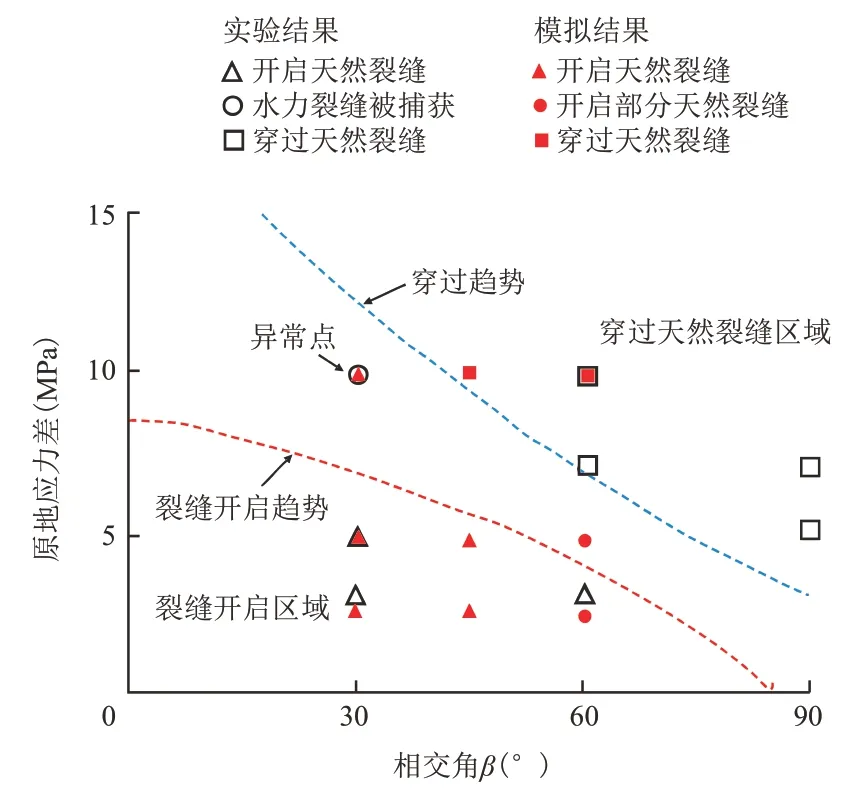
图16 模型计算结果与实验结果对比Fig.16 Comparison diagram of model calculation results and experimental results
3 结论
基于相场法理论建立了多孔介质中水力压裂裂缝延伸模型,通过3个不同时间步长算例验证了研究模型的收敛性。将模型计算结果与前人物理模拟实验结果进行对比,验证了模型的正确性。另外,利用该模型研究了原地应力差、相交角、注入速率和压裂液黏度对含天然裂缝地层中水力裂缝延伸特征的影响,得到的主要认识如下:
1)相交角和原地应力差越小,水力裂缝越容易开启天然裂缝,但即使相交角和原地应力差很小,水力裂缝也只能开启天然裂缝的一翼。
2)较高的注入速率有利于完全开启天然裂缝。注入压力随注入速率的增加而增加。因此,在压裂施工过程中,在井口装备和地下管柱强度允许的条件下应尽量提高施工排量。
3)注入压力随着压裂液黏度增加而增加,水力裂缝长度随着压裂液黏度增加而略有减小。
