压裂过程数据对原始煤储层压力反演方法研究

石军太，李文斌，张龙龙，季长江，李国富，张遂安

（1.中国石油大学（北京）油气资源与探测国家重点实验室，北京102249；2.中国石油大学（北京）煤层气研究中心，北京102249；3.煤与煤层气共采国家重点实验室，山西晋城048012）

中国煤层气储量可观，位居全球第三，地质资源量为30.05×1012m3，有巨大开发潜力[1]。其中原始煤储层压力的评价对煤层气的开发至关重要[2]，它可直接影响煤层气藏类型的划分[3-7]、煤层气的储量计算[8-10]、排采制度的优化设计等环节[11-14]。原始煤储层压力一般通过油气井中途测试（DST）和注水压降试井确定，其中DST 的主要目的是求取煤储层的整套参数。由于在钻井过程中运用DST 测试的煤储层压力接近原始煤储层压力，故在实际生产前通常用DST 获得原始煤储层压力[15]。而评价储层压力最直接的方法是试井，煤层气藏一般采用注入/压降测试以评价原始煤储层压力，注入/压降测试是一种将水或者2 %的KCl 水溶液以低于煤层破裂压力的注入压力和一定排量注入地层一段时间后关井，使压力逐渐降落并与原始煤储层压力逐渐平衡的试井方法[16-18]。但上述方法中DST测试需多次开井关井，且对于低压煤储层，测试前的施工可能将施工液注入煤层，对煤层气藏渗透率伤害较大。同样使用注入/压降试井方法时，通常需要暂停生产一段时间进行注入溶液，这会导致煤层气井再次生产时容易发生产量波动、骤降甚至不产气。不同学者也在尝试研究其他求取原始地层压力方法，陈江萌、杨玲等[19-20]针对低渗气藏提出了求取平均地层压力的计算方法，但都需要进行关井，这同样会影响煤储层的渗透率以及实际生产。刘林松等[21]提出了一种不关井求取原始地层压力的方法，但是仅选用两组生产数据，选用资料较少，可靠性不易保证。

针对中国大部分煤层气藏低渗、低压、非均质性强、变质程度高以及储层构造复杂等特点[22-28]，以及大部分煤层气井需采取水力压裂等增产措施才能商业开发的现状[29-33]，采用压裂过程中井口压力数据求取原始煤储层压力的方法值得探索。目前由于压裂过程中裂缝网络渗透率变化过程很难在商业压裂模拟软件中体现[34-38]，导致商业压裂模拟软件求取的原始煤储层压力存在较大误差。截至目前，鲜有学者考虑压裂后裂缝网络渗透率变化特征对原始煤储层压力计算的影响。因此，基于渗流力学理论，考虑压后裂缝网络渗透率变化的影响，建立了一种应用水力压裂关井阶段井口压力降落数据计算原始煤储层压力的方法，并且对该方法进行了实例验证和应用。

1 模型建立

一煤层气井水力压裂后关井，压裂和关井期间压裂液向地层渗流，基本假设为：①煤储层为原生结构煤，无夹矸，且水平、均质、等厚、各向同性、横向无限大；②煤层气井注入压裂液前地层中各点的压力均匀分布，压裂中气井以定排量注入；③地层流体和岩石微可压缩，压缩系数不发生变化；④地层流体流动符合达西渗流定律；⑤考虑稳态表皮效应，即看成是井壁无限小薄层上的压降；⑥忽略重力和毛管力的影响；⑦煤层中压裂裂缝的形状除了具有主裂缝外，还存在辐射状的裂缝网络，井周围流体的流态可近似视为平面径向流，示意图见图1。

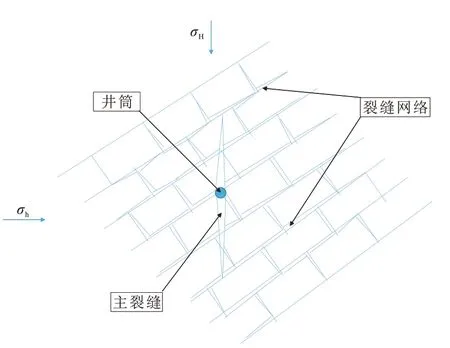
图1 煤层压裂后形成的裂缝网络示意图Fig.1 Schematic diagram of fracture network formed after coal seam fracturing

应用地下流体渗流理论，可得煤层中压力势的渗流方程如方程组（1）所示：

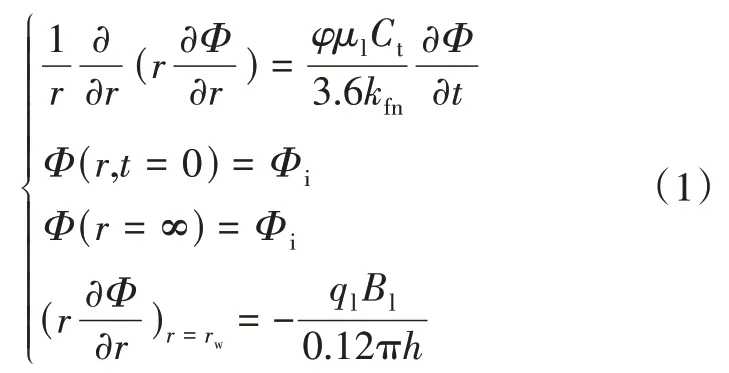
式中：Φ为地层势函数，（µm2·MPa）/（mPa·s）；φ为地层孔隙度；μl为压裂液黏度，mPa·s；Ct为综合弹性压缩系数，MPa-1；kfn为煤储层压裂后裂缝网络渗透率，µm2；Φi为原始地层势函数，（μm2·MPa）/（mPa·s）；ql为压裂液排量，m3/min；Bl为压裂液体积系数，m3/m3；r为距离井口的距离，m；t为时间，h；rw为井半径，m；h为地层厚度，m。

可假设rw=0，方程组（1）的解可简化为：

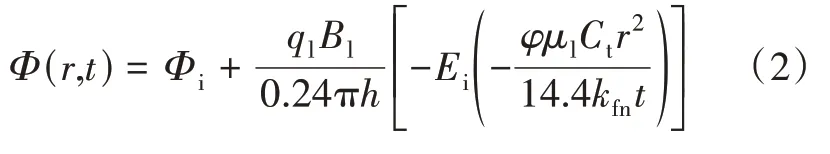
式中：Ei为指数积分函数。

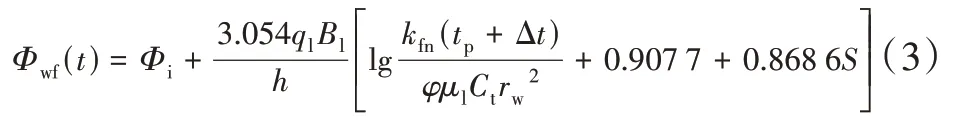
式中：Φwf为井底势函数，（µm2·MPa）/（mPa·s）；tp为压裂液注入时间，h；Δt为关井时间，h；S为表皮系数。

由此可利用叠加原理来分析煤层气井注水后关井期间井底势函数的变化情况，可将一口煤层气井以排量为ql注入tp时间后关井测试过程假设为两口井井底势函数的叠加：一口井从0 时刻开始以ql排量注入至关井结束，另一口井从tp时刻以ql产量采出至关井结束。由此t=tp后，假设煤层气井继续向地层注入压裂液，势函数变化为：

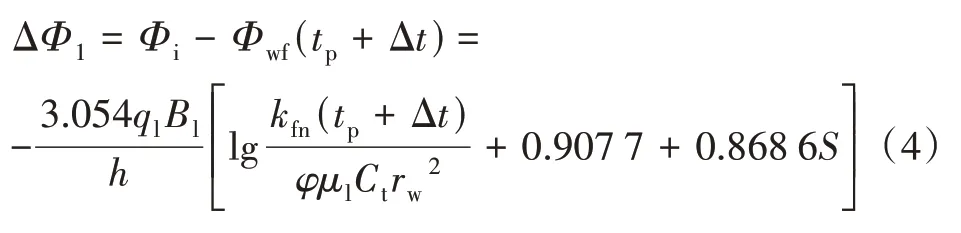
在tp时，气井关井测试，相当于一口虚拟采出井，势函数变化为：

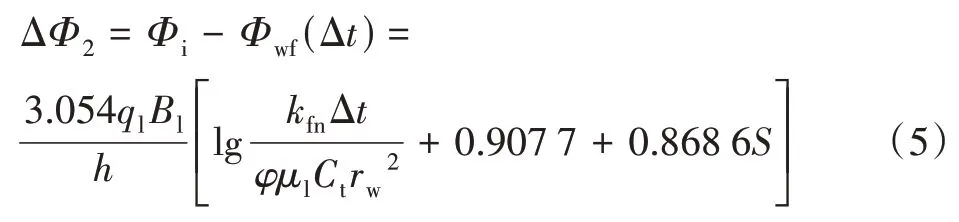
（tp+Δt）时刻，势函数叠加：

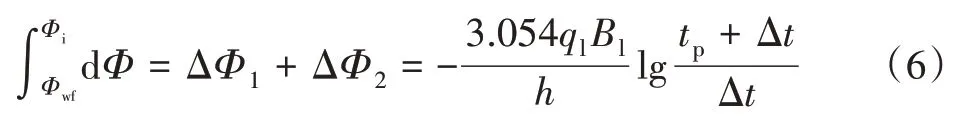
式（4）—式（6）中：ΔΦ1为虚拟注入井井底势函数变化量，（µm2·MPa）/（mPa·s）；ΔΦ2为虚拟采出井井底势函数变化量，（µm2·MPa）/（mPa·s）。

2 求取原始地层压力方法推导

2.1 忽略裂缝网络渗透率变化

由于已知势函数公式为：

式中：p为当前煤储层压裂后裂缝网络所受地层压力，MPa。

当忽略裂缝网络渗透率变化时，kfn与μl为常数，因此，由式（6）可得井底流压计算公式为：

式中：pwf为井底压力，MPa；pi为原始煤储层压力，MPa。

其中，压裂液稳定注入时间tp可用包括总压裂液量和钻井滤失量在内的总注入液量除以稳定的压裂液排量而得到，计算公式为：

式中：Vl为总注入液量（总注入液量中不包含加砂量），包括总压裂液量和钻井滤失量，m3。

由于关井过程中可监测井口压力变化，根据液柱压力计算公式，可以计算得到井筒液柱压降为：

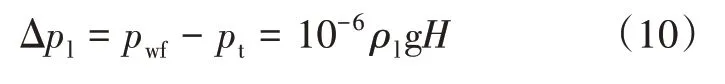
式中：Δpl为井筒液柱压降，MPa；pt为油管压力，MPa；ρl为井筒中压裂液密度，kg/m3；g为重力加速度，m/s2；H为煤层埋深，m。

将式（10）代入式（8）中整理可得井口油管压力变化为：

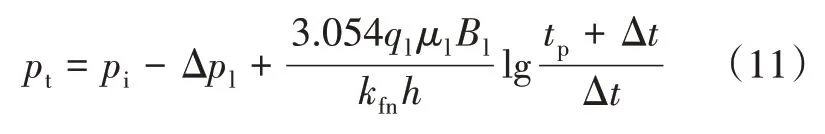
令：

因此，以无因次时间lg((tp+Δt)/Δt)为X轴，油管压力pt为Y轴可绘制散点图。并分析煤储层压裂后裂缝网络渗透率变化并计算稳定后渗透率。由式（11）进一步化简，可令：

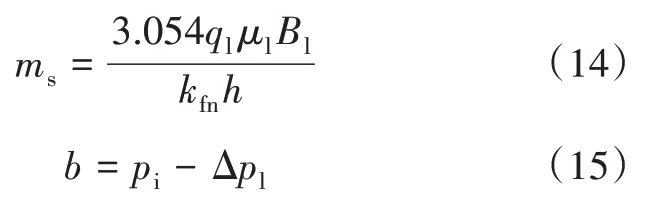
式中：b为直线纵轴截距，MPa；ms为应用压裂后关井后期的数据点拟合直线的斜率，MPa。

整理可得：

式中：m为普适性的直线斜率，MPa。

由此可知，若煤储层压裂后裂缝网络渗透率一定时，ms为常数，无因次时间lg((tp+Δt)/Δt)与井口油管压力pt具有线性关系。则煤储层压裂后裂缝网络渗透率可根据直线斜率ms、煤储层厚度、压裂液排量、压裂液黏度和压裂液体积系数的值，应用计算得出。

通常情况下，煤层气井压裂后关井，煤储层压裂后裂缝网络渗透率逐渐降低并趋于稳定。可以通过绘制无因次时间lg((tp+Δt)/Δt)与井口油管压力pt的散点图，分段线性拟合，观察斜率变化，进而分析压裂后煤储层裂缝网络渗透率的变化趋势。因此，应选取压裂后关井后期的数据点，拟合直线，求出应用压裂后关井后期的数据点拟合直线的斜率ms。根据直线斜率，可计算出煤储层压裂后裂缝网络渗透率的具体数值：

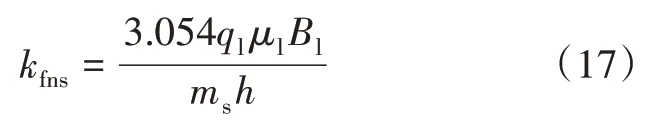
式中：kfns为煤储层压裂后裂缝网络稳定的渗透率，µm2。

进一步运用压裂后关井后期的数据点拟合直线的纵轴截距bs，求得原始煤储层压力：

式中：bs为压裂后关井后期的数据点拟合直线的纵轴截距，MPa。

2.2 考虑裂缝网络渗透率变化求取原始地层压力

由于煤储层应力敏感性较强[38]，压后关井期间，孔隙压力降低，有效应力增加[39]，裂缝闭合、支撑剂迁移、煤粉迁移、部分支撑剂可能嵌入煤层，造成煤储层裂缝网络渗透率逐渐降低[37]。煤储层压裂后裂缝网络渗透率为压力的函数[38,40]：

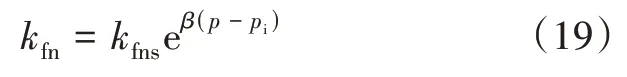
式中：β为煤储层压裂后裂缝网络渗透率变化指数，MPa-1。

若考虑压裂后关井期间煤储层裂缝网络渗透率的变化，kfn此时不为常数，应参与积分。由式（6）可知井底流压计算公式为：

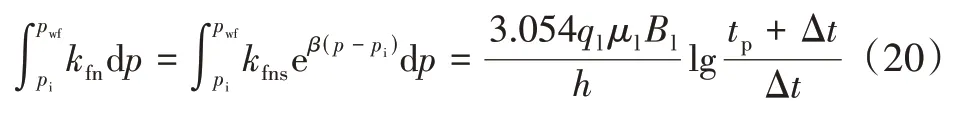
积分公式（20），并根据式（10）将井底流压换算到井口油管压力，可得出井口油管压力变化的表达式：

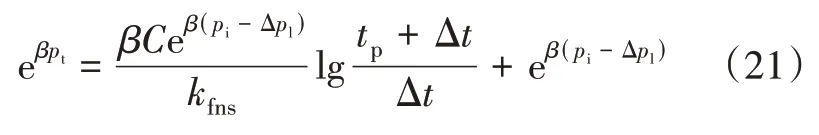
其中：

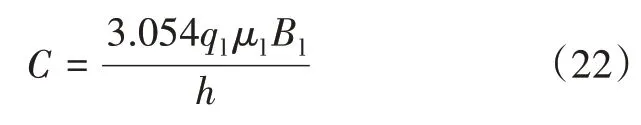
式中：C为煤储层压裂常数，MPa·µm2。

由式（21）可令：

因此，以无因次时间lg((tp+Δt)/Δt)为X轴，无因次油管压力函数eβpt为Y轴，并去除关井时刻不稳定数据可绘制散点图。由式（21）进一步化简，可令：

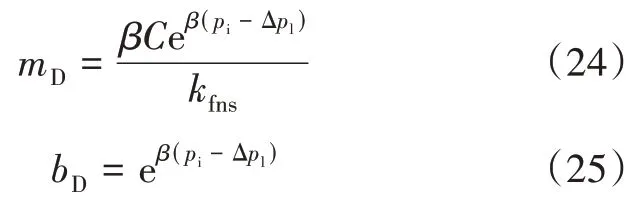
整理可得：

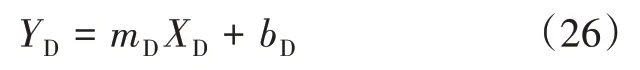
式中：YD为无因次油管压力函数；mD为无因次油管压力函数与无因次时间图中拟合直线的斜率；bD为无因次油管压力函数与无因次时间图中拟合直线的纵轴截距。

拟合直线，根据bD和mD，可计算煤储层压裂后裂缝网络稳定的渗透率的具体数值：

进一步，根据直线的纵轴截距bD，可求得原始煤储层压力：

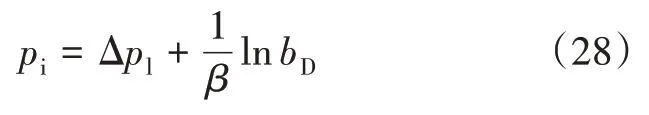
3 实例应用

实例选取了一口煤层气井W 的压裂数据资料进行分析，W 井所用压裂液密度为1 000 kg/m3，体积系数为1 m3/m3。压裂液稳定排量为8 m3/min。W 井煤层埋深755.49 m，煤储层厚度4.90 m，总压裂液量650 m3，经过多次调整确定的渗透率变化指数0.07 MPa-1，压裂施工数据见图2。

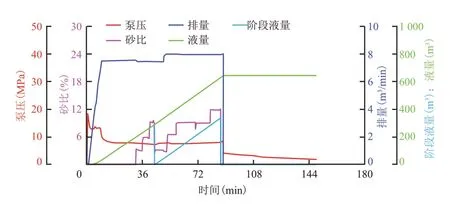
图2 W井煤层压裂施工综合曲线Fig.2 Comprehensive curve of coal seam fracturing of Well-W

将总压裂液量Vl与压裂液稳定排量ql代入式（9）可计算压裂液注入时间tp=1.354 h。并根据液柱压力计算公式，将煤层埋深H、压裂液密度ρl以及重力加速度g 代入式（10）计算得到W 井井筒液柱压降为Δpl=7.403 8 MPa。

3.1 忽略裂缝网络渗透率变化

以无因次时间lg((tp+Δt)/Δt)为X轴，油管压力pt为Y轴绘制散点图（图3）。

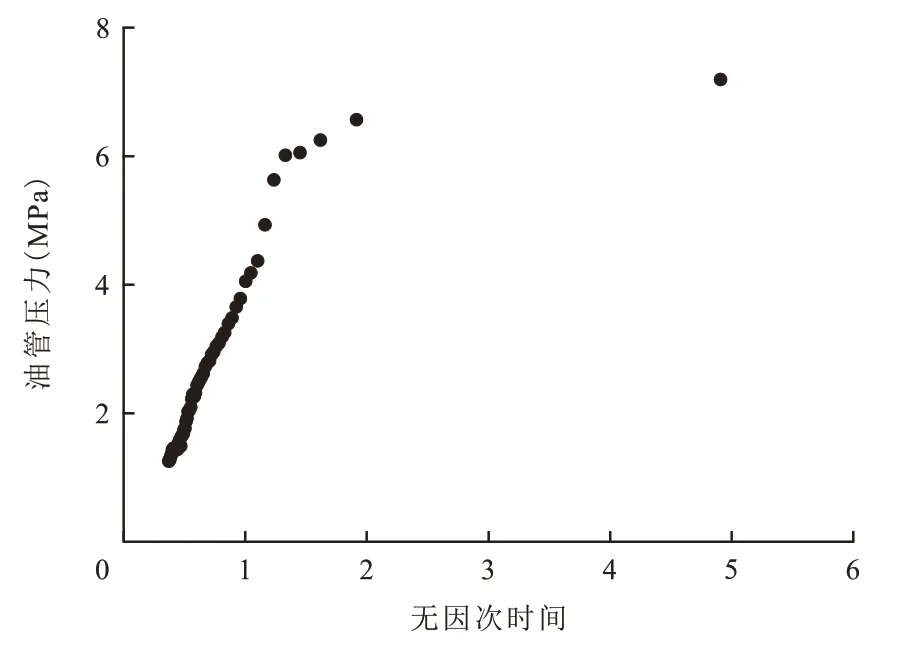
图3 油管压力与无因次时间散点Fig.3 Scatter plot of tubing pressure and dimensionless time

已知在煤储层压裂后裂缝网络渗透率一定时，无因次时间lg((tp+Δt)/Δt)与井口油管压力pt具有线性关系Y=mX+b，因此可绘制散点图并进行分阶段线性拟合（图4）。

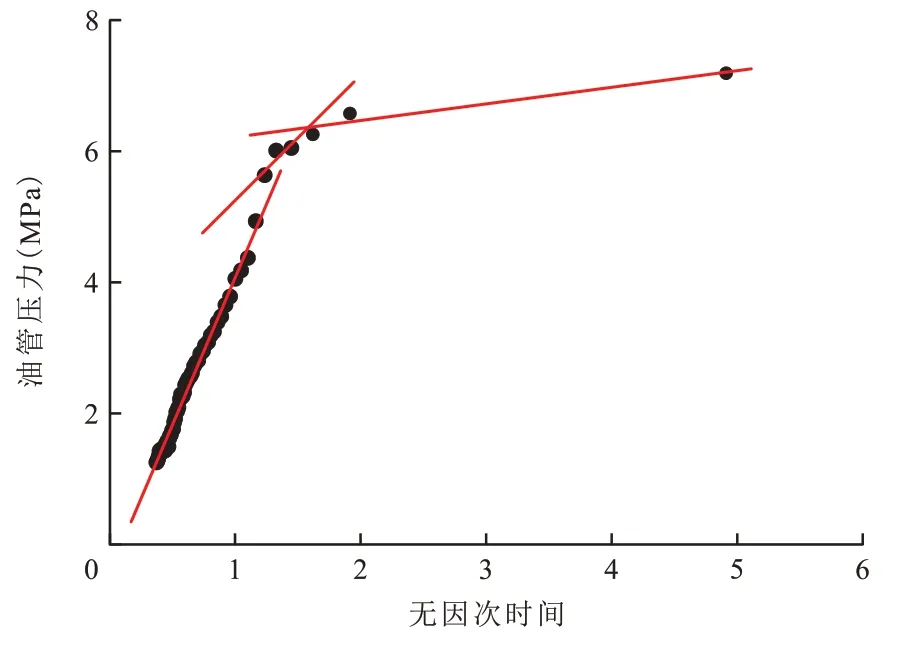
图4 油管压力与无因次时间分段拟合Fig.4 Piece wise fitting plot of tubing pressure and dimensionless time

W 井注入压裂液关井后，压裂液向地层中渗流。由图4 可知随着关井时间增加，无因次时间逐渐降低，因此斜率随着时间逐渐增大，可得知煤储层压裂后裂缝网络渗透率逐渐降低并趋于稳定[37]。选取压裂后关井后期的数据点，拟合直线（图5）。

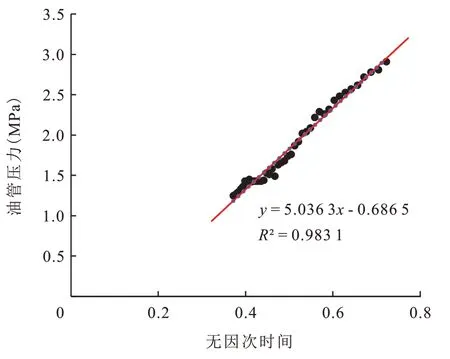
图5 稳定阶段油管压力与无因次时间线性拟合Fig.5 Linear fitting plot of tubing pressure and dimensionless time in stable stage

由图5可知，压裂后关井后期的数据点拟合直线的斜率ms=5.036 3 MPa，将求得直线斜率ms、煤储层厚度h、压裂液稳定排量ql、压裂液体积系数Bl以及压裂液黏度μl代入式（17）可计算煤储层压裂后裂缝网络稳定的渗透率kfns=1.488 2 µm2。压裂后关井后期的数据点拟合直线的截距bs=-0.686 5 MPa，将bs值与W 井井筒液柱压降Δpl代入式（18），计算得到W 井所在原始煤储层压力pi=6.717 3 MPa。

3.2 考虑裂缝网络渗透率变化

将压裂液稳定排量ql、压裂液体积系数Bl、压裂液黏度μl以及煤储层厚度h代入式（22）可求得C=7.479 MPa·µm2。并以无因次时间lg((tp+Δt)/Δt)为X轴，无因次油管压力函数eβpt为Y轴绘制散点图，经过多次调整确定的渗透率变化指数β的数值，使直线拟合效果最好，最终确定出β等于0.07时直线拟合效果最好。无因次油管压力函数eβpt和无因次时间lg((tp+Δt)/Δt)存在明显线性关系（图6）。

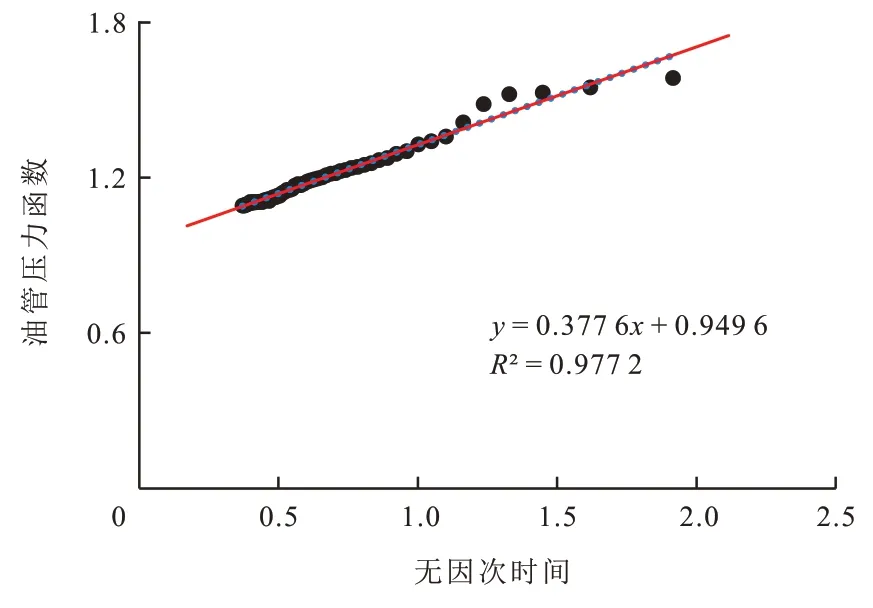
图6 W井无因次油管压力函数与无因次时间拟合Fig.6 Fitting plot of dimensionless tubing pressure function and dimensionless time for Well-W

图6 可知，直线斜率mD=0.377 6，截距b=0.949 6，将煤储层裂缝网络渗透率变化指数β、煤储层压裂常数C以及直线斜率mD和截距bD代入式（27），可计算W 井煤储层压裂后裂缝网络稳定的渗透率为kfns=1.316 6µm2。进一步运用W 井拟合直线的纵轴截距bD，将W 井的井筒液柱压降Δpl、煤储层裂缝网络渗透率变化指数β以及拟合直线截距bD代入式（28），求得W井的原始煤储层压力pi=6.665 0 MPa。

3.3 结果分析与讨论

通过对比以上是否考虑压裂后关井期间煤储层裂缝网络渗透率变化，所求得的原始煤储层压力和煤储层裂缝网络稳定的渗透率，发现两种方法解释的数值较为接近。当忽略煤储层裂缝网络渗透率的变化过程，解释的煤储层裂缝网络稳定的渗透率为1.488 2µm2，原始煤储层压力为6.717 3 MPa；而当考虑压后关井期间煤储层裂缝网络渗透率的变化过程，解释的煤储层裂缝网络稳定的渗透率为1.316 6µm2，原始煤储层压力为6.665 0 MPa，与区块内早期测试井的测试结果更为吻合。由于煤储层压裂过程和压后关井期间煤储层裂缝网络渗透率变化是客观存在的，并且在压裂过程中裂缝的延伸促使煤岩微通道结合水向自由水转化，渗透率也会有所改善，因此考虑压后关井期间煤储层裂缝网络渗透率变化所求得的原始地层压力和渗透率更加符合实际。而忽略煤储层裂缝网络渗透率的变化过程的方法，假设煤储层裂缝网络渗透率后期达到完全稳定。事实上，随着压力降低，煤储层裂缝网络渗透率依然会逐渐降低，只是降低的幅度越来越小。综上所述，在计算煤层原始地层压力时，有必要考虑压裂后煤储层裂缝网络渗透率的变化。

4 结论

1）考虑压后裂缝网络渗透率变化的影响，应用压裂后井口关井压力数据，提出了一种新的原始煤煤层压力反演方法。该方法只需将压后关井时间处理为无因次时间，将井口油管压力数据处理成为无因次油管压力函数，作图进行线性拟合，根据拟合直线的斜率和纵轴截距即可计算出原始煤储层压力。

2）建立的原始煤储层压力反演方法通过现场实例验证发现拟合结果线性关系明显，所用数据容易获取并且计算简便，反演结果与区块内测试井测试结果一致，表明建立的应用压裂过程数据反演原始煤储层压力的方法可靠有效。

3）该方法考虑到了煤储层压裂过程和压后关井期间煤储层裂缝网络渗透率变化的客观现象，因此在计算原始煤储层压力时考虑压后裂缝网络渗透率的变化是十分有意义的。

4）该方法基于压裂过程中压裂液主要在裂缝和宏观孔隙中渗流，且满足达西渗流的假设条件，未考虑压裂液在微孔隙中的渗吸现象。对于压后长时间关井的煤层气井，压裂液在微孔隙中的渗吸作用不可忽略，该方法解释的结果将存在一定误差。综合考虑裂缝、宏观孔隙中的达西渗流和微孔隙中的渗吸机理，建立原始煤储层压力反演方法，是下一步的研究方向。