用高观点揭示一类导数压轴题的本质

范明辉

(湖北省荆门市龙泉中学 448000)

1 问题的提出

例1(2015年全国高考Ⅱ卷第12题)设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(-1)=0，当x>0时，xf′(x)-f(x)>0，则使得函数f(x)>0成立的x取值范围是( ).

A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)

C.(-∞,-1)∪(1,+∞) D.(-1,0)∪(0,1)

上例中出现了“xf′(x)-f(x)>0”的结构式，解决此类问题需要构造辅助函数.对于此类题目，有一些常见结构式的辅助函数构造方法：

(1)若f(x)+xf′(x)>0(或<0)，可构造辅助函数g(x)=xf(x)；

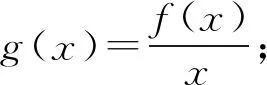
(3)若nf(x)+xf′(x)>0(或<0)，可构造辅助函数g(x)=xnf(x)；

(5)若f(x)+f′(x)>0(或<0)，可构造辅助函数g(x)=exf(x)；

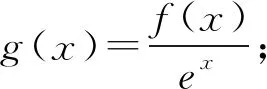
在日常教学中，教师一般会要求学生熟记以上常见结构式的辅助函数，然后再加以训练来巩固记忆，然而，此类题目往往只有少数学生能够成功解决.问题的关键在于，如何去构造这样的辅助函数？构造方法是怎样的？有没有一般的步骤呢？

2 “辅助函数”的构造原理(基于不定积分原理)

对于结构为y′+P(x)y=Q(x)的方程，结合求导法则[u(x)v(x)]′=u′(x)v(x)+u′(x)v(x)，将方程两端同乘以一个非零因子r(x)，得

r(x)y′+r(x)P(x)y=r(x)Q(x).

①

对比求导法则(yr)′=y′r+yr′，得

r′(x)=r(x)P(x).

对上式两边同时积分,得

②

将②式代入①式,得

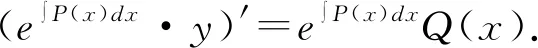
③

2.1 结构为y′+P(x)y=0的形式

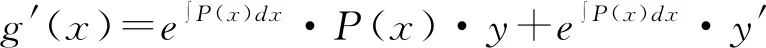
此时函数g(x)的导函数中包含方程的左边部分P(x)y+y′，而在高中相关类型导数题中往往给出了这部分与零之间的不等关系，从而可以判断出函数g(x)的单调性，进而结合函数知识求解.

2.2 结构为y′+P(x)y=Q(x)的形式

若Q(x)≠0，则y′+P(x)y=Q(x).

可变形为y′+P(x)y-Q(x)=0.

④

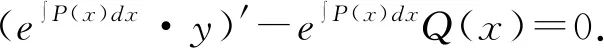
⑤

结合求导法则[u(x)-v(x)]′=u′(x)-v′(x)，可将⑤式进一步变形为

因此，可构造“辅助函数”

此时函数g(x)的导函数中包含④式的左边部分y′+P(x)y-Q(x)，而在高中相关类型导数题中往往给出了这部分与零之间的不等关系，从而可以判断出函数g(x)的单调性，进而结合函数知识求解.

此类结构的构造原理，基于不定积分的相关方法，读者可以深入了解，也可略过.

3 结构为P(x)f(x)+f ′(x)的类型

例1解析当x>0时，xf′(x)-f(x)>0，

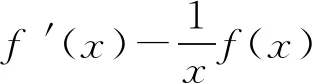
因此可构造辅助函数g(x)=e-lnx·f(x).

当x>0时，g′(x)>0，

所以g(x)在(0,+∞)上单调递增.

由于函数f(x)为奇函数且f(-1)=0，所以g(x)为偶函数，且g(-1)=g(1)=0.

因此，g(x)在(0,+∞)上单调递增，在(-∞,0)上单调递减.要求函数f(x)>0成立的x取值范围，则xg(x)>0，易知x∈(-1,0)∪(1,+∞)，故选A.

下面对结构式为P(x)f(x)+f′(x)类型的算法步骤进行总结：

(1)将题设条件中的结构式化归为P(x)f(x)+f′(x)，即让“f′(x)”的系数变为1；(2)找到P(x)，并借助导数公式寻找其一个原函数φ(x)；(3)构造辅助函数g(x)=eφ(x)·f(x).

按照上述步骤，我们再来看一看常见结构的构造方法：

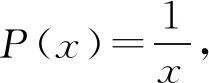
(5)若f(x)+f′(x)>0(或<0)，则P(x)=1，其一个原函数为y=x，因此可构造辅助函数g(x)=exf(x)；

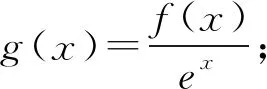
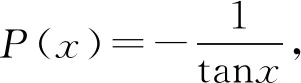
4 结构为f ′(x)+P(x)f(x)-Q(x)的类型

例2(2009年天津文科高考题)设函数f(x)在R上的导函数为f′(x)，且2f(x)+xf′(x)>x2，下面的不等式在R上恒成立的是( ).

A.f(x)>0 B.f(x)<0

C.f(x)>xD.f(x)

解析因为2f(x)+xf′(x)>x2，

所以2f(x)+xf′(x)-x2>0.

求导，得g′(x)=2xf(x)+x2f′(x)-x3.

即g′(x)=x[2f(x)+xf′(x)-x2].

综上，f(x)>0，故选A.

下面对结构式为f′(x)+P(x)f(x)-Q(x)类型的算法步骤进行总结：

(1)将题设条件中的结构式化归为f′(x)+P(x)f(x)-Q(x)，即让“f′(x)”的系数变为1；(2)找到P(x)，并借助导数公式寻找其一个原函数φ(x)；(3)利用求导公式寻找eφ(x)Q(x)的一个原函数ψ(x)；(4)构造辅助函数g(x)=eφ(x)·f(x)-ψ(x).

此类问题一般出现在选择题或填空题的压轴题位置，难度较高，其难点在于构造出“辅助函数”.经过本文的探究，找到了构造相应“辅助函数”的一般步骤，将难点转化为“逆用导数求导公式，寻找导数的原函数”.