页岩储层应力敏感性定量评价:思路及应用1)

2022-08-30杜书恒沈文豪赵亚溥

力学学报 2022年8期

关键词：杨氏模量泊松比渗透率

杜书恒沈文豪赵亚溥 ,2)

*(中国科学院力学研究所非线性力学国家重点实验室,北京 100190)

† (中国科学院大学工程科学学院,北京 100049)

**(太原理工大学机械与运载工程学院,太原 030024)

引言

随着全球能源需求的迅速增长和非常规油气勘探开发的持续推进,页岩油气在世界能源结构中的重要地位日益凸显[1-4].与北美相比,我国页岩油气储层总体具有埋藏深、地质构造复杂、有机质成熟度低、岩石非均质性强、开采难度高等显著特征.页岩储层的复杂力学行为及演化机理已成为提升采收率实践中被卡住的“最细的脖子”[5-7].

渗透率的确定贯穿于页岩油勘探开发各个时期及各个领域.作为页岩最为关键的地质参数之一,不同开发时期页岩渗透率的准确评估是决定实时产能变化趋势预测精度的重中之重[8-11].一般而言,常规储层渗透率大多为基于Darcy 定律,借助常规岩心驱替设备测试得到的,测试结果被广泛应用于浅层常规储层评价[12-13].然而,由于该数值为常温常压下测得,与处于深部温压环境中的页岩属性可能存在一定差异.为解决这一问题,前人在恢复页岩储层原位条件方面做了大量有益的探索[14-16],但由于力、化、热、流耦合理论和实验材料匹配等理论与技术壁垒,现有室内测试技术尚不能精确获取原位渗透率参数.因此,如何实现页岩储层原位渗流性能的定量评估仍有待探索.

事实上,深部页岩作为胶结程度较高的细粒沉积岩,随着油气运移或开采等因素引起的内部流体的持续减少,其岩石骨架承受的有效应力将逐渐增加,进而引起内部孔隙、微裂缝发生压缩,最终导致渗透率损失、产能下降,上述现象称为页岩储层的“应力敏感”[17-19].大量研究及实践显示,其科学与工程意义主要体现在两个方面:(1)页岩应力敏感性评估精度直接影响页岩油气原位储量计算的准确程度.只有在厘清储层应力敏感规律的前提下才能有效确定储层常规物性参数向原位物性参数的转化标准,进而计算真实储量[19-20];(2)应力敏感程度是确定油田现场合理生产压差的核心参数.只有定量明确储层应力敏感特征,才能实现页岩油的安全高效开采,即应力敏感性认识的准确程度直接影响采收率提升幅度[21-22].因此,如何实现应力敏感性的科学定量评价是页岩油气勘探与开发中公认的工程科学难题,亟待深入研究.

为解决上述问题,常使用固定有效应力下页岩渗透率与其初始渗透率的比值或定义各类岩石压缩系数来评价与比较不同岩石的应力敏感程度相对高低[23-26].然而,有关流道尺寸变小和渗透率下降的幅度究竟有多大,下降的规律究竟如何等问题,学界的观点碰撞仍然较为尖锐,至今尚无定论.调研发现,众多学者通过开展大量变应力条件下页岩渗透率的室内实验测试,依据实验结果相继构建或修正了众多描述渗透率与有效应力之间关系的理论评价模型,主要包括指数型[27-28]、幂指数型[29-30]和多项式型[31-32]三类,但其公式中核心参数的物理意义仍有以待进一步厘清,作为经验模型其应用范围亦将受到研究区域的限制.此外,在针对该问题的理论及实验研究中,学术界形成了两种截然相反的观点,分别为“页岩渗透性越差,应力敏感性越强”和“低渗页岩并不存在强应力敏感”[33-35].持第一种观点的学者主要是基于大量实验的观测与统计,而持第二种观点的学者则质疑了实验测试中的三个核心问题[36-38]:(1) 实验载荷方式的技术局限将导致岩石无法达到实际受力状态;(2) 岩心封套与岩心间存在的微间隙将导致渗透率测试过程中的较大幅度误差;(3) 由于流量计计量精度和测试人员的经验差异所限,对渗透率测试中稳态时刻的判断在一定程度上带有主观色彩,测试结果误差较大.

从工程实践来看,应力敏感性地层在开采过程中应与地表沉降、地层垮塌现象相伴生.这一现象在疏松高渗储层中较为常见,但较少在页岩储层中发现.这与实验测试结果显示的“渗透率越低则应力敏感性越强”的结论相悖[39-40].事实上,现场开发效果与室内实验结果契合度不高甚至结论相反的现象并不罕见,本文认为解决这一矛盾的方法除了审视实验本身的问题,还应从理论上加以推导、完善.

1 页岩应力敏感性定量评价

1.1 研究思路

本文总体研究思路如图1 所示.在充分认识页岩应力敏感现象的重要意义并考虑页岩孔缝非均质性的前提下,联合Griffith 经典弹性力学解、椭圆管Poiseuille 方程和Darcy 定律,结合岩石本体变形中孔隙度不变形原则,分别推导得到基质型页岩与裂缝型页岩应力敏感程度评价公式和覆压渗透率计算公式[41].

图1 总体研究思路:(a)页岩油储层应力敏感现象及规律示意图;(b)页岩油原位储量预测示意图;(c)页岩油真实产能评估示意图;(d)页岩油储层应力敏感性定量评价示意图Fig.1 The overall research idea of this study:(a) schematic of the stress sensitivity and law in shale oil reservoir;(b) schematic of in-situ reserves prediction of shale oil;(c) schematic of the actual productivity evaluation of shale oil;(d) schematic of the quantitative evaluation of stress sensitivity in shale oil reservoir

通过选取基质型和裂缝型页岩油储层的实际样品,结合已有的关键实验数据开展实例应用,对中国西部和中部两类页岩油储层的应力敏感特征开展定量评价,为工程现场提供相关启示或指导.

1.2 基质型页岩应力敏感程度评价公式推导

Inglis[42]在1913 年分析了平板椭圆孔的尖端应力集中现象,Griffith[43]在1920 年用弹性能转换的观点推导了平板椭圆孔裂纹扩展的临界应力值.图2中,椭圆孔的横坐标x范围在[-a,a]区间内,应力作用下椭圆短轴方向张开宽度d(x)的表达式为

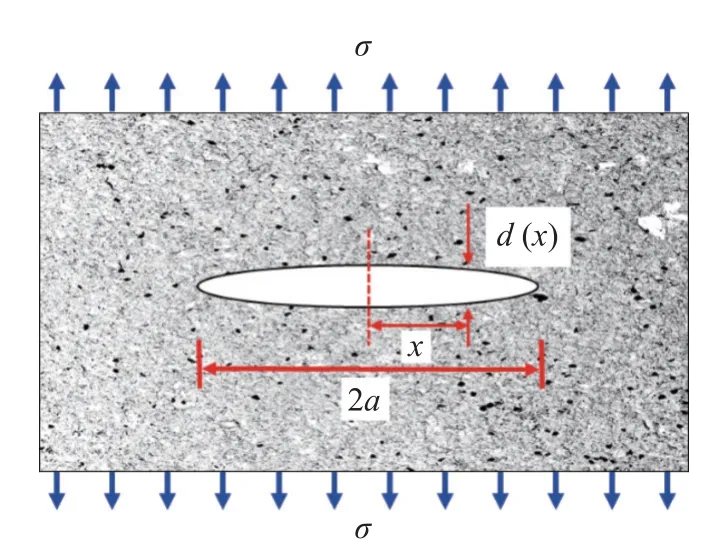
图2 Griffith 裂纹扩展条件推导示意图Fig.2 Schematic of the growth conditions derivation of Griffith crack

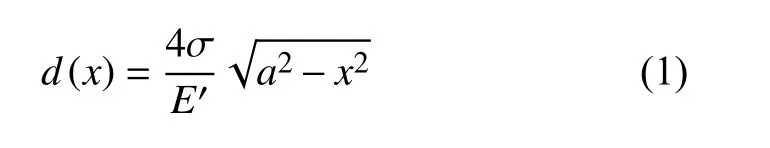
平面应力条件下,E′=E;平面应变条件下E′=

当椭圆的长短轴相等时,椭圆即退化成圆,因此圆孔仅为椭圆孔的一个特例.另外,当椭圆的长短轴比值逐渐增大时,其形态逐渐趋向于裂缝.因此,选择椭圆孔分析应力状态,其结论更具一般性,易于推广.

当前岩石多孔介质物理研究中广泛使用了标准圆柱管束模型来等效岩石储层中的孔隙和微裂缝[44-45].为进一步突出页岩油储层的非均质性,本次选用横截面为椭圆的柱体管束模型作为孔隙的等效模型.显然,当椭圆的长短轴数值相同时,上述模型即退化为标准圆柱管束模型.此外,当椭圆长轴远大于短轴时,椭圆可进一步向裂缝趋近.因此,对于包含了孔隙和裂缝的页岩而言,建议椭圆管束模型可增强研究结论的一般性,便于推广.需要指出的是,为了充分挖掘应力敏感现象的本质,对于单根管束而言,本文沿用经典毛细管定义,假设垂直该管束方向的截面面积相同,即单根毛细管内径是均匀分布的.对不同管束而言,其横截面积是呈现非均质分布的.

由于储层岩石占据三维空间,因此在载荷条件下,岩石内部产生的应力、应变必然是三向的,属于弹性力学空间问题.当然,若岩石形状具备某种特征时,可将其转换为弹性力学平面问题[41,46].基质型页岩内部主要发育孔隙,微裂缝比例相比较低,可忽略不计.如图3 所示,假设岩石中只含有一个横截面为椭圆的管束通道,该管束在纵向(Z)上的尺寸远大于横向(X,Y)上的尺寸,二者约相差6 个数量级.同时,在压缩过程中,所有外力均与纵轴(Z)垂直且沿纵轴无变化.椭圆孔所有横截面上对应点(X,Y坐标相同)的应力、应变和位移均相同,可作为平面应变问题处理.因此,只需沿管束纵向截出单位厚度的管束进行分析,用以代替整个管束的研究.

图3 横截面为椭圆的柱体管束模型示意图(基质型页岩)Fig.3 Schematic of cylinder tube bundle model with elliptical cross section (matrix-type shale)

事实上,岩石中含有大量管束,为问题处理方便起见,将所有管束等效为一个管束通道,使该管束通道与储层岩石的体积之比等于岩石孔隙度.需要指出的是,中国页岩油气储层的孔隙度值总体处在1%～10%之间,即孔隙所占体积比整块岩石体积小1～ 2个数量级.因此,岩石应力敏感过程其实是图1 椭圆孔张开的逆过程,即等效椭圆孔的闭合过程.

压缩过程中,随着有效应力大小的增加,椭圆孔逐渐缩小,短轴方向的间距逐渐减小,减小量为 Δd.假设岩石中的椭圆孔在受到有效应力压缩之前具有初始半短轴长b0.由于该问题属于平面应变问题,在某一固定的有效应力值条件下,椭圆孔的半短轴长度满足[41-43]

式中 σe是以拉应力为正的有效应力.根据Terzaghi有效应力原理,在不考虑孔隙内部压力的情况下,文中所指的有效应力即为岩石骨架承受的压力即岩石外压[31,36].

单个椭圆管束流动的Poiseuille 方程为[47]

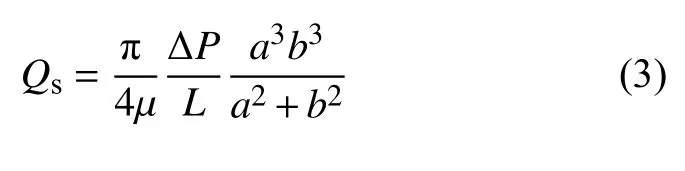
若岩石中含n个管束,则总流量为

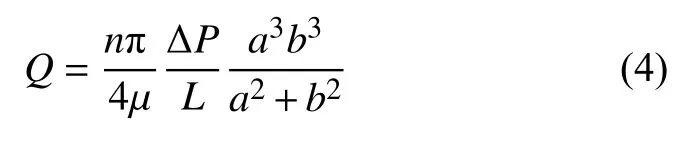
式中,Qs和Q分别为单个椭圆管束流量和总流量,μ为流体黏度,a和b分别为椭圆管束横截面的长轴与短轴尺寸,ΔP为流动方向的压强差.

含有n个管束的岩石有效孔隙度φ为

其中,A为岩石横截面积.结合多孔岩石中的Darcy定律

联立式(2)、式(4)和式(5)可得储层渗透率基本表达式为

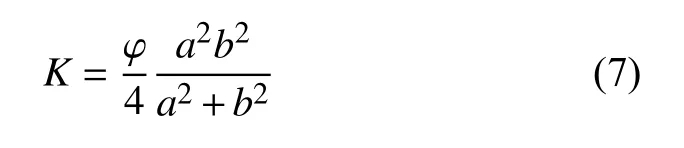
因此,初始渗透率K0和不同有效应力状态下的渗透率K′的表达式分别为

压缩前后孔隙度表达式分别为

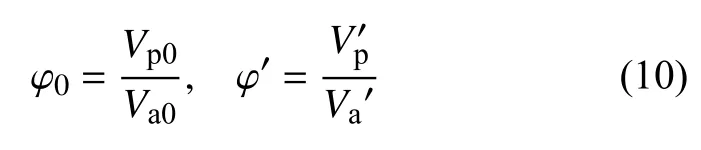
式中，Vp0，Va0分别为有效应力为0 时的初始岩石孔隙体积和外观体积.分别为不同有效应力状态下的岩石孔隙体积和外观体积.

根据致密岩石本体变形中的孔隙度不变性原则[48],对于具有高胶结程度的页岩而言,在其弹性极限内的应力加载压缩过程中,孔隙体积变形来源于颗粒体积变形,即岩石外观体积的变形程度与孔隙体积的变形程度相同,即

本文定义“渗透率保持水平”用以评估应力变化导致的岩石渗透率的变化程度.渗透率保持水平是指随着有效应力的增加,岩石在不同时刻的渗透率与有效应力为0 的状态下的渗透率的比值.数值越接近1,说明应力引起的渗透率变化规模越小,渗透率相对初始而言保持的程度越高,应力敏感程度越低;反之,数值越接近0,说明应力引起的渗透率变化规模越大,渗透率相对初始而言保持的程度越低,应力敏感程度越低.

联立式(8)～式(11)可得,应力作用下岩石渗透率保持水平的表达式为

将式(2)代入上式可得

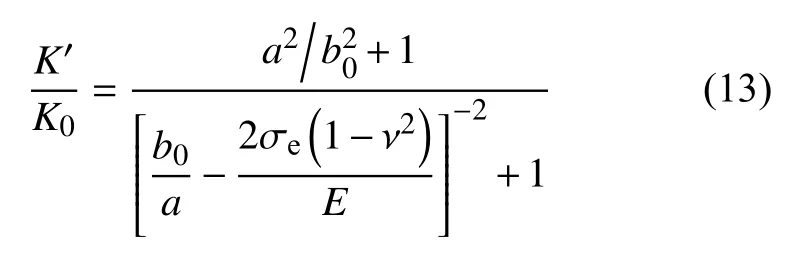
所以应力敏感性将由四个因素共同决定,即储渗空间长短轴比值a/b0、岩石骨架杨氏模量E、岩石骨架泊松比ν和有效应力 σe.

当有效应力为零时,K′/K=1,即不发生应力敏感,符合实际.对于相同状态下的固定岩石样品而言,岩石骨架杨氏模量E,岩石骨架泊松比ν和长短轴比值a/b0均为常数且符号为正.此时,随着有效应力不断增加,K′/K将由1 逐渐降低,发生应力敏感.

若基质型页岩油储层初始渗透率是在一定的初始有效应力值σe0下测得时,上述公式亦可进一步拓展为

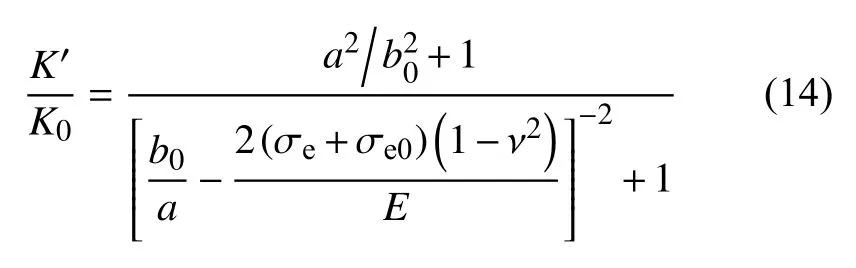
因此,基质型页岩油储层覆压渗透率K′的表达式为

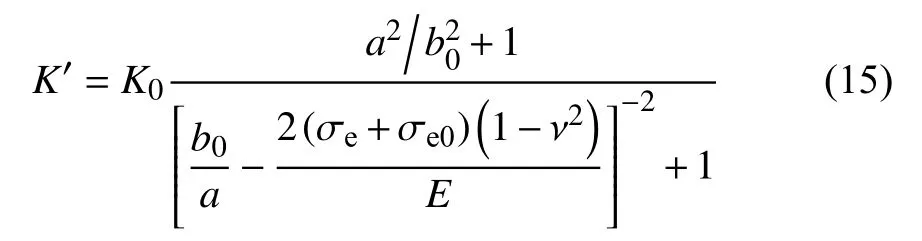
1.3 裂缝型页岩应力敏感程度评价公式推导

裂缝型页岩内部主要发育微裂缝,基质孔隙比例较低,本次研究中不予考虑.而且,当岩石内部含有主裂缝时,其余微裂缝的作用亦可忽略.

假设岩石样品内部含有一条主裂缝(图4),相似地,由Poiseuille 方程和Darcy 定律可得含主裂缝储层渗透率表达式为

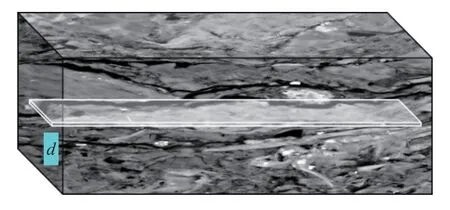
图4 微裂缝模型示意图(裂缝型页岩)Fig.4 Schematic of microcrack model (fracture-type shale)

将微裂缝等效为椭圆孔,则等效椭圆孔的短轴长的二倍可近似为微裂缝宽度d,即d=2b,所以

初始渗透率和不同有效应力状态下的渗透率的表达式分别为

相似地,渗透率保持水平的表达式为

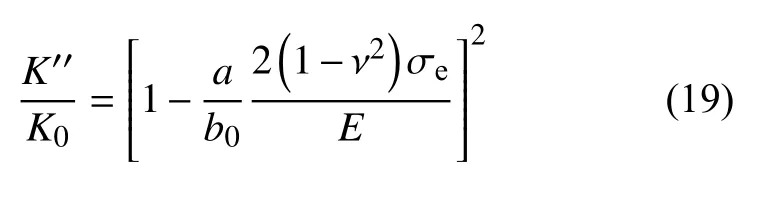
若裂缝型页岩油储层初始渗透率是在一定的初始有效应力值σe0下测得时,上述公式亦可进一步拓展为

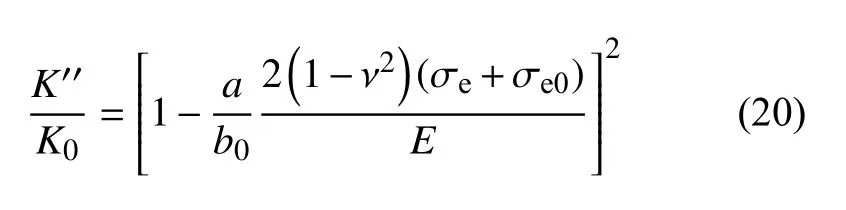
因此,裂缝型页岩覆压渗透率K′′的表达式为

2 工程实例应用

2.1 基质型页岩

选取准噶尔盆地芦草沟组页岩油储层岩石样品,开展场发射扫描电镜成像实验.成像结果显示(图5),该页岩样品主要以基质孔隙为主,微裂缝发育程度较低,属于典型的基质型页岩油储层.

图5 基质型页岩场发射扫描电镜成像结果(准噶尔盆地芦草沟组)Fig.5 Imaging results of matrix-type shale under field emission scanning electron microscope (Lucaogou formation,Junggar Basin)

基于图像处理平台对所有孔缝开展等效椭圆拟合,得到a/b0主要分布在1～ 9 之间.具体流程为:对储层样品开展高分辨率电镜成像,利用图像处理平台确定孔隙-颗粒分割的最佳灰度阈值,进而提取出所有孔隙个体.对所有孔隙个体开展勒让德椭圆拟合,得到相应椭圆的长轴a和短轴b,由此可计算得到所有孔隙个体的a/b0数值.结果显示,本研究中的基质型页岩油储层样品的a/b0主要分布在1～ 9之间.相关岩石力学实验数据显示[49],研究区页岩油储层杨氏模量数值主体分布在10～ 35 GPa 之间,泊松比数值主体分布在0.2～ 0.3 之间.同时,为全面刻画应力敏感变化特征,将有效应力设定为0～40 MPa.上述数据将用于分析页岩应力敏感特征.

2.1.1a/b0改变

取页岩杨氏模量E的平均值为23 GPa,泊松比取值为0.25,a/b0分别取1～ 9,当有效应力在0～40 MPa 变动时,应力敏感特征曲线为图6 所示.

图6 a/b0 为变量的基质型页岩应力敏感曲线Fig.6 Stress sensitive characteristic curve of matrix-type shale with a/b0as variable

随着a/b0的不断变化,基质型页岩应力敏感程度总体极其微弱,最大渗透率损耗程度不足6%.随着a/b0的增大,渗透率下降速率逐渐增大,应力敏感程度均匀增强,证明对于基质型页岩而言,孔隙扁平程度越高,越容易被压缩.

2.1.2 泊松比改变

取页岩杨氏模量E的平均值23 GPa,a/b0取平均值为5,泊松比数值分别取0.2～ 0.3,当有效应力在0～ 40 MPa 变动时,应力敏感特征曲线为图7所示.

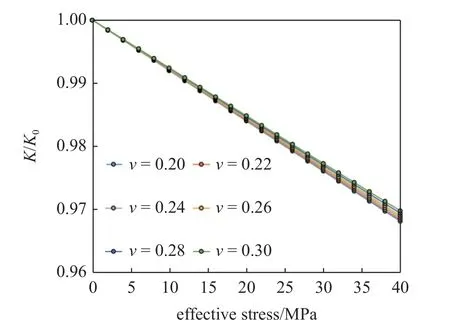
图7 泊松比为变量的基质型页岩应力敏感曲线Fig.7 Stress sensitive characteristic curve of matrix-type shale with Poisson's ratio as variable

随着泊松比的不断变化,基质型页岩应力敏感程度总体极其微弱,最大渗透率损耗程度不足4%.随着储渗泊松比的增大,渗透率下降速率逐渐减小,应力敏感程度均匀减小,但减小幅度总体较低,即泊松比对于岩石应力敏感性影响程度并不显著.总体而言,泊松比越大,孔隙越不易被压缩.

2.1.3 杨氏模量改变

a/b0取平均值为5,泊松比取值为0.25,页岩杨氏模量E取10～ 35 GPa,当有效应力在0～40 MPa 变动时,应力敏感特征曲线为图8 所示.

图8 杨氏模量为变量的基质型页岩应力敏感曲线Fig.8 Stress sensitive characteristic curve of matrix-type shale with Young's modulus as variable

随着杨氏模量的不断变化,基质型页岩应力敏感程度总体亦极其微弱,最大渗透率损耗程度不足8%.随着杨氏模量的增大,渗透率下降速率逐渐变缓,应力敏感程度均匀降低.证明杨氏模量越大,孔隙越不易被压缩.

2.2 裂缝型页岩

选取鄂尔多斯盆地延长组页岩油储层岩石样品,开展场发射扫描电镜成像实验.图9 显示,该页岩样品主要发育基质孔隙,微裂缝发育比例较低,属于典型的裂缝型页岩油储层.

图9 裂缝型页岩场发射扫描电镜成像结果(鄂尔多斯盆地延长组)Fig.9 Imaging results of fracture-type shale under field emission scanning electron microscope (Yanchang formation,Ordos Basin)

对所有孔缝开展椭圆拟合,得到a/b0主要分布在1～ 19 之间.相关岩石力学实验数据显示[50],研究区页岩油储层杨氏模量数值主体分布在20～40 GPa 之间,泊松比数值主体分布在0.18～ 0.24 之间.相似地,为全面刻画应力敏感变化特征,将有效应力设定为0～ 40 MPa.上述数据亦将用于分析该类裂缝型页岩油储层应力敏感特征.

2.2.1a/b0改变

取页岩杨氏模量E的平均值30 GPa,泊松比取值为0.21,a/b0分别取1～ 19,当有效应力在0～40 MPa 变动时,应力敏感特征曲线见图10.

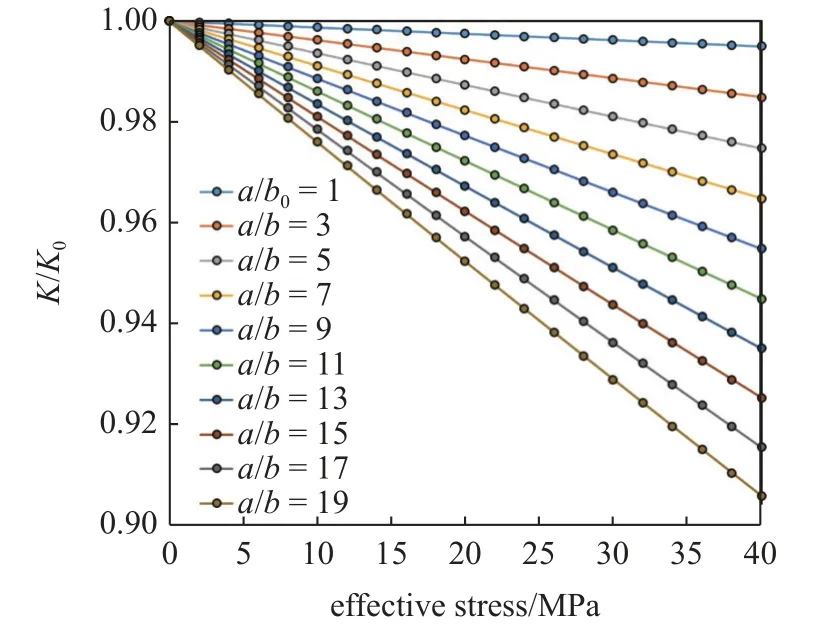
图10 a/b0 为变量的裂缝型页岩应力敏感曲线Fig.10 Stress sensitive characteristic curve of fracture-type shale with a/b0 as variable

随着a/b0的不断变化,裂缝型页岩应力敏感程度总体较为微弱,最大渗透率损耗程度不足10%,应力敏感程度总体大于基质型储层.随着a/b0的增大,渗透率下降速率逐渐增大,应力敏感程度均匀增强.

需要指出的是,虽然上述所有孔缝的椭圆长短轴比值分布在1～ 19 之间,数值跨度较大,但由于裂缝型页岩中仍含有一定数量的基质型孔隙,导致其总体平均值仅为2.0,且纵横比大于4.0 的孔缝占比不到6%.这表明,纵横比能达到4.0 以上甚至19 的孔缝在鄂尔多斯盆地延长组页岩油储层中仅为少数.对于选取的实例样品而言,纵横比的平均水平维持2.0 左右,这与裂缝型页岩中微裂缝发育的非均质性密切相关.图10 中全面展示了椭圆长短轴比值1～ 19 的范围内的全部应力敏感特征曲线,旨在评估裂缝型页岩应力敏感的最高水平,进而突出结论的一般性,并不代表实际页岩中的平均孔缝纵横比值能达到19.实际上,即使平均纵横比值达到19,页岩应力敏感程度亦维持在10%以内的低水平,进一步凸显了裂缝型页岩弱应力敏感的事实.

2.2.2 泊松比改变

取页岩杨氏模量E的平均值30 GPa,a/b0取平均值9.5,泊松比数值分别取0.18～ 0.24,当有效应力在0～ 40 MPa 变动时,应力敏感特征曲线为图11 所示.

图11 泊松比为变量的裂缝型页岩应力敏感曲线Fig.11 Stress sensitive characteristic curve of fracture-type shale with Poisson's ratio as variable

随着泊松比的不断变化,基质型页岩应力敏感程度总体极其微弱,最大渗透率损耗程度不足5%.随着泊松比的增大,渗透率下降速率逐渐减小,应力敏感程度均匀减小,但减小幅度总体较低,即泊松比对于岩石应力敏感性影响程度并不显著.

2.2.3 杨氏模量改变

a/b0取平均值为9.5,杨氏模量取20～ 40 GPa,泊松比取值为0.21,当有效应力在0～ 40 MPa 变动时,应力敏感特征曲线为图12 所示.

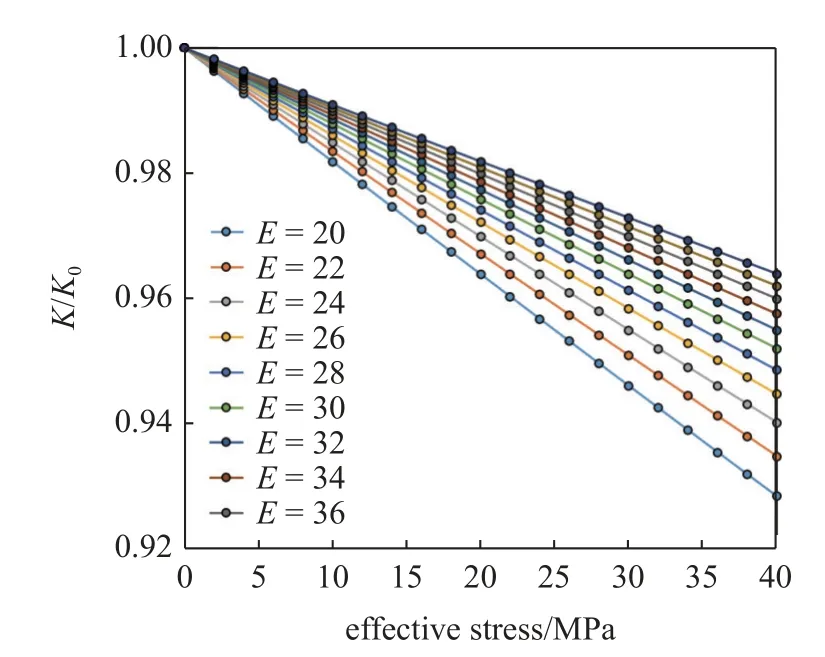
图12 杨氏模量为变量的裂缝型页岩应力敏感曲线Fig.12 Stress sensitive characteristic curve of fracture-type shale with Young's modulus as variable

随着杨氏模量的不断变化,基质型页岩应力敏感程度总体亦较为微弱,最大渗透率损耗程度不足8%.随着杨氏模量的增大,渗透率下降速率逐渐变缓,应力敏感程度均匀降低.

以40 MPa 有效应力下的基质型和裂缝型页岩为例,随着杨氏模量的增大,在起始阶段,应力敏感程度迅速降低,然后降低幅度逐渐趋小.裂缝型页岩总体应力敏感程度高于基质型页岩,且杨氏模量越小,二者应力敏感程度差异性越大(图13).

图13 变杨氏模量条件下基质型和裂缝型页岩应力敏感曲线对比(有效应力40 MPa)Fig.13 Comparison of stress sensitive characteristic curve of matrixtype and fracture-type shale under variable Young's modulus (effective stress value is 40 MPa)

对比前人模型结果发现[35,38],40 MPa 有效应力条件下,岩石应力敏感程度总体均小于5%,亦可为页岩储层总体呈现低应力敏感特征提供佐证.

为进一步厘清上述三类参数影响页岩应力敏感的显著程度,对杨氏模量、泊松比、a/b0等参数数值进行归一化处理,分析结果显示相同应力状态下,a/b0、杨氏模量、泊松比对页岩的应力敏感的影响程度依次降低.

2.3 本文力学模型的延伸性讨论

本文力学模型应用了以下几个假设:骨架在变形过程中满足线性弹性、变形状态可以使用小应变理论描述、岩石外观体积应变和孔隙体积应变相等、骨架始终没有出现破坏.固体骨架始终处于线性弹性状态,这与岩石为弹脆性材料相符,描述剪胀、非线性弹性等现象则需要引入适当的力学模型[41].小应变理论要求固体骨架的应变和变形量都很小,所以可以使用Cauchy 应变描述任意位置的变形,对于有限变形问题可以在本模型基础上进一步探索研究.当岩石外观体积应变和孔隙体积应变相等,代表有效应力仅引起固体骨架体积变形而非微结构的畸变,说明孔隙内存在与有效应力大小相等的压强的作用,进一步表明岩石、骨架、孔隙三者的体积应变相等,并且孔隙度保持不变,需要注意如果孔隙内存在流体,孔隙体积应变并非孔隙流体的体积应变.

当弹脆性多孔介质在加载过程中内部微结构出现破坏时,孔隙由于局部碎裂而闭合,容易产生伪塑性现象而服从弹塑性损伤本构关系[51].从材料力学或者断裂力学的角度来看,孔隙越小则微结构的承载能力越强,材料整体的弹性段就越长,本文模型适用的载荷范围也就越广.一般情况下孔隙尺寸和孔隙度成正比,初始孔隙度越高的材料,越容易发生微结构的破坏,当有效应力增加时也越容易产生孔隙闭合现象,一个典型的本构方程的例子是Drucker-Prager 帽子模型[41],此时压实状态对应应力空间中的“帽子”也越低.页岩油在开采过程中可能出现微结构破坏等不可逆变化,进而形成新的流动通道.此时,渗透率将由于新通道的形成而有所提升,且升高程度与这些微结构的破坏情况密切相关.需要指出,由于应力敏感性的研究主题为应力增加条件下引起的岩石渗透率的损耗,因此上述微结构破裂引起的增渗现象并不属于应力敏感性研究的范畴,本文所选用力学模型对于研究页岩应力敏感问题是合适的.

如果放松岩石外观体积应变和孔隙体积应变相等的假设,需要考虑受力时骨架和孔隙的应变之比.假设椭圆孔均匀分布在岩石中,并且沿椭圆长短轴方向的密度之比为长短轴尺寸之比a/b0.可将岩石分为每个截面单元具有一个椭圆孔的代表性长方形网格,其边长为n为每单位面积的孔隙数量.沿短轴压缩后岩石和椭圆孔的体积应变分别为

式中,k=(1+ν)(1-2ν),则压缩变形前后孔隙度之比为

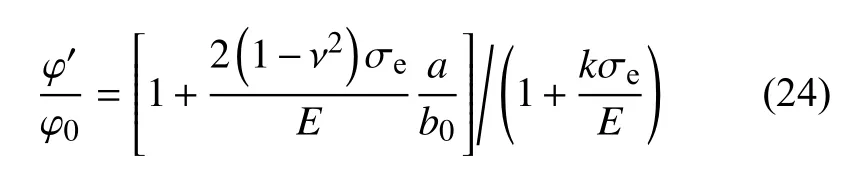
所以有效应力作用下岩石当前和初始渗透率之比为

式中

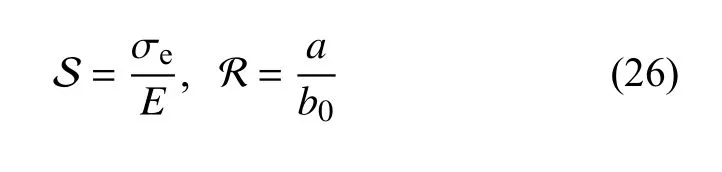
分别是无量纲有效应力和椭圆孔的长、短轴之比.应力敏感性程度仍然由三个因素共同决定,即原始长短轴比值a/b0、岩石骨架泊松比和无量纲有效应力.该式满足在无应力加载时,敏感性程度为零,且随着压应力增加渗透率减小的现象;当孔隙长短轴之比为无穷大时,即 R →∞,上式退化为裂隙介质受压前后的渗透率之比.可以看出对于裂隙来说任意微小的压应力都将使渗透率降为0,这与绝对光滑裂缝受压时的物理直观相符,可以通过研究裂隙面粗糙度的影响来进一步完善应力敏感性程度的评价公式.

以煤层气储层为代表的煤系地层内部发育了大规模的割理裂隙系统,储层孔隙度极低而渗透率较高,与页岩储层存在本质区别.同时,煤层的杨氏模量多分布在1～ 7 GPa,普遍低于页岩[52-53].有效应力的改变除了引起煤层固体骨架的体积变形外,也将造成较大规模的微结构畸变.此时,煤层、骨架、孔隙三者的体积应变已不再相等,孔隙度亦将持续变化,与页岩[54-61]、砂岩[55,62-67]、砾岩[68-73]、碳酸盐岩[74-81]等沉积岩储层都应加以区别.