复杂时间序列的多尺度分析1)
2022-08-30高剑波
高剑波
(北京师范大学地理科学学部地理数据与应用分析中心,北京 100875)
引言
20 世纪科学巨匠冯·诺伊曼临谢世时,对死亡后的人不再有思维,感到迷惑和恐惧.自2021 年8 月25 日吾师郑哲敏先生逝世至今,我有时也有这样的感觉,因不能与先生电话或面谈而得到先生对某件事的看法.但有时又觉得好像不全如此,因为先生的思维方式至少部分传下来了.在这篇纪念先生的文章里,我想在谈学术研究前,先提一下先生对我个人的影响.这些影响基本决定了我在非线性领域和其他领域研究问题的偏好.本文主要介绍先生和我在非线性领域的一些工作,及后来这些工作如何被拓展并演变成一些通用的非线性问题的分析方法.这些方法已被广泛用于自然科学、工程技术和社会科学的诸多领域.它们特别适用于各领域(包括运维)的故障诊断,生物医学数据的分析,及不确定性的度量.大家要是觉得有些方法对研究有用,请随时联系我,索要相关程序和使用说明.
1 教诲
1988 年,我从浙江大学工业自动化专业毕业.在浙大时,跟数学老师周先意先生,学了不少数学.周老师是陈建功和苏步青先生的学生,是数学家王元的同班同学.周老师在1958 年被发配到江西农村.空余时间都在思考教数学时如何把分析、代数和几何融合起来.1978 年苏步青先生将其调回浙大.由周老师教我们数学,是我们的幸运.周老师对学生极好,跟我们聊天时经常提到4 个他最得意的学生,曹银和博士便是其中之一,其时他已在北京力学所,师从白以龙院士,跟郑先生也熟.来京前,我没见过曹师兄,但经常与其通信交流.
1987 年大三时,在浙大电机系,我听了一个外校教授关于混沌动力学的报告,觉得这个领域太迷人了,因此跟曹师兄提及,并表示以后很想做这方面的研究.其时力学所正筹划于次年6 月建立非线性连续介质力学开放实验室(LNM),并由郑先生挂帅,所以曹师兄问我是否愿意去力学所跟郑先生读研.我自然很激动.之后曹师兄又带来一个好消息,说郑先生会帮我办理保送手续,这样就不用担心因没学过力学而考不上(不像现在考研,当时只考专业课),这些沟通发生在1987 年10 月.至11 月下旬,出了些问题,曹师兄跟我说,郑先生因太忙,忘了去给我申请免试读研,而申请的截止期是11 月1 号.所以师兄问我,是否等一年再说.我想了想,说还是考吧.考试在2 月初.我花了2 个月,学了4 门力学课,考上了力学所.
我在力学所待了6 年.第一年在玉泉路的研究生院,与先生几乎没有接触.后5 年,几乎随时可以找先生聊.在LNM 刚开始时,真正做非线性的年轻人就两三位,包括何国威院士、赵力师兄和我.可惜,我因资质有限,当时学得很有限.下面我讲五个方面.
第一点与情怀有关.在追思先生时,很多人提到先生说过的一句话,“不要做锦上添花的事,要做雪中送炭的事”.这个情怀的精髓是坚持不懈地努力,做出最好的工作.这包含两个方面.一是对自己的要求.听说先生90 岁高龄时还自己推导公式.二是帮助学生和年轻人,做出最好的工作.记得2007 年,我寄给先生我的英文著作[1]后,先生很喜欢,随即建议我寄一本给冯元祯先生.冯先生是生物医学工程奠基人之一,生物力学之父,是郑先生最好的朋友.冯先生当时已是88 岁高龄.开会时经常碰到加州大学的教授说,冯先生如此高龄,每年还会在PNAS 上发表高质量的文章,太令人敬佩.在书寄给冯先生后,近一个月,没收到任何回音,我忐忑不安,心里默念是不是自己书写得不好或冯先生的专业与我相差较多.此时,冯先生的亲笔书信到了,信中特别强调,他在每一页都学到了一些新东西.我特别激动,告知了郑先生信的内容,先生也很高兴.冯先生的鼓励对我影响很大.冯先生在信中还建议我看看他的好友,美国工程院院士黄锷(Norden Huang)关于经验模态分解(empirical mode decomposition,EMD)的工作[2].冯先生太有洞见了!他看出了我们数据分析的体系还缺类似于EMD 的一块.所幸,当时我们已经发展了一个新方法.这在第4 节会讲到.总的来说,冯先生的提醒,很大地促进了我们发展自适应去趋势、去噪、多尺度分解和分形分析.
另一件事,好像是2010 年初秋,先生还在美国探访儿子.我回国探亲,回美时,路过北京.远在美国的先生安排我去拜访林家翘先生.因郭永怀先生和李佩先生是林先生的好友,郑先生托李佩先生带我去清华拜访林先生.当时林先生已是95 岁的高龄了.到了林先生的别墅,聊了一个多小时,只聊一个主题,如何理解蛋白质结构.林先生最出名的工作是流体力学的流动稳定性和星系螺旋结构的密度波理论,但关于此却一字未提.不囿于自己熟悉的领域,随着时代发展不断拓展新的领域,这就是大师们的情怀.身处百年未遇之大变局时期,我们必须发扬光大大师们的这种求真务实和开拓创新的精神.
第二点与心态有关.2002 年8 月,我在佛罗里达大学当助理教授,其时离开力学所和郑先生已有8 年,自己首次带研究生,我想,怎么教能好些呢?脑袋里突然冒出来一句先生跟我讲过的话:100%的相信,同时又要120%的怀疑.先生的高明之处在于,不用另外解释,我自然觉得这句话很有道理.在我指导学生时,还展开解释了,所以落了下乘:前半句,100%的相信,表示对所选的领域和问题的重要性和前瞻性没有任何怀疑,因此会全身心、充满激情地投入到学习和研究中,只有这样,才能将天赋真正变成才能,并发挥出来.后半句,表示在所选的领域中,一些最基本的东西都可能有错.说的俗一些,就是不要被权威所束缚.其实,朴实的心态应该是,充分欣赏领域里那些漂亮的工作,但不该有谁是权威、能否超越等想法,而应该努力找到所选问题的最佳解,并成为最好的专家之一.虽然我不如先生高明,但这个教学方法还是有效的,如我在佛罗里达大学的博士生胡静,深得此法的精髓,对后面第3,4 节描述的方法,有很大的贡献.
第三点与思考有关.先生与我聊天时,强调最多的是,要自由思考.刚到力学所时,有朋友劝我一定要多读郑先生出名的那些文章.但因我缺乏基础,同时当时看不到那些工作与非线性科学的关系,且郑先生也没有要求我读,所以在力学所的几年,基本没读过郑先生的文章.2014 年,在庆祝郑先生90 岁生日的会议上,与我很熟的一位老教授,谈庆明老师,跟我说,当年我进力学所时,郑先生特意嘱咐他们,不要限制小高,让他完全自由发展.谈老师特别强调,郑先生这样关照的,我是绝无仅有的一个.听谈老师这么说,我很感动,也很惭愧.我想主要是我没力学背景,所以郑先生特别关照我.当然,由此也可看出郑先生对非线性科学的重视.可惜,1994 年出国后,有近10 年时间,我只断断续续地作为业余爱好者继续做些非线性问题的研究,所以成绩很有限.
第四点是宽容.事情得从1989 年秋天我在LNM 做的报告说起.郑先生请了很多人来听,包括北京大学的朱照宣先生.那是我做的第一个报告,讲得自然很不好,很多人听后有些不满意.不过,会上郑先生没有批评我,会后更没约束我的思维.
后来我没有转行做量子计算,理由是,大尺度、宏观的量子纠缠态几十年内是没法实现的,因此不可能发展出能用于通用计算的量子计算机.这个推理不一定严谨,但决定是正确的,21 世纪量子计算、量子通信需要的是实验方面的俊才,但于此我不擅长.另外,1993 年,MIT 的Cuomo 和 Oppenheim[3-4]用Pecora 和 Carroll[5]发展的混沌同步开创了用混沌做安全通讯的新领域.在1998 年前后,美国海军研究部的Pecora 博士组织了一个多学科大学研究计划(Multidisciplinary University Research Initiative,MURI,类似 DARPA 的项目) 以推动混沌安全通讯的军用和民用的研究.参加项目的有加州大学圣地亚哥分校(UCSD)、加州大学洛杉矶分校(UCLA)和斯坦福大学.其时,我在UCLA 电子工程系跟随Rubin 教授读博.系里的两位老师,Jia-Ming Liu 教授和Kung Yao 教授,参与了MURI 项目.姚教授做通讯,刘教授用半导体激光实现通讯.我对此很感兴趣,参与了刘教授团队的工作,因此与几位同学,Steven Huang、Howard Chen、Shuo Tang 和 C.C.Chen 成了好朋友.前三位是刘教授的学生,最后一位是姚教授的学生.除了Shuo Tang 去英属哥伦比亚大学当教授,其他三位都去了台湾当教授.与他们讨论时,我告知C.C.Chen,混沌通讯的功耗应该比Cuomo等[5]所说的大,因Cuomo 等在模拟随机微分方程时,把随机项处理错了(成正比,但Cuomo 等用dt代替了 dt—当 dt≪1 时,≫dt,相当于将实际噪声缩小了几个数量级,因而得出功耗小的结论).C.C.Chen 和姚教授发现我是对的,因而证明,混沌通讯也许能用于军用,但在民用领域,价值很有限[6-7].之后,这方面研究的热度在美国大降,但在香港和欧洲仍持续了很久.
第五点一定要重视科学实验和实验数据分析,尽量从重大的现实问题中,抽象出具有根本科学意义的问题,然后同时解决现实和科学问题.我想这是从普朗特传至冯·卡门、冯·卡门传至钱学森、再由钱学森传至郑哲敏的技术科学的精髓.
2 混沌时间序列分析
为了不让我成为无根的浮萍,谈庆明老师建议郑先生让我跟一个研究圆柱尾流混沌现象的实验团队一起做研究.这个项目的立项,白老师和曹师兄起了很大作用.团队由林贞彬和鄂学全两位老师领衔,成员中有位动手能力极强的年轻人,李东辉.团队研究的目的是通过测量和分析圆柱尾流固定点速度分量的时间序列来厘清圆柱尾流的初始转捩区域是否存在混沌现象,若是,再继续研究混沌在湍流发展过程中的作用.
自1963 年Lorenz[8]发表Lorenz 混沌方程至20 世纪八九十年代,混沌现象的基本特性及由规则运动向混沌运动转化的机制都已清楚.前者包括分数维特征和系统对初值的敏感性,后者包括周期倍化至混沌[9]、准周期至混沌[10]及间歇性至混沌[11]等路径.这里只粗略介绍一下最基本的概念和现象,更详细的请见文献[1,12].系统对初值的敏感性指的是小扰动随时间呈指数增长.令d(0)为0 时两条任意轨迹之间的小距离,d(t)为时间t时它们之间的距离,对于真正的低维确定性混沌,我们有

其中,λ1被称作最大的Lyapunov 指数.混沌吸引子的轨迹在相空间中有界.相邻轨迹的指数发散导致的不断拉伸,加上吸引子的有界性引起的不时折叠,使混沌吸引子经常成为分形,其特征是
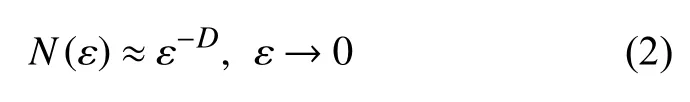
其中,N(ε) 表示在相空间中完全覆盖吸引子所需的线性长度不大于 ε 的(最小)盒子数.D称为吸引子的计盒维数.通常它是一个非整数.对于混沌 Lorenz吸引子来说,D为2.06.值得指出,方程(2)也适用于度量无人经营过的山路或海岸线的长度.这种情况,D通常大于1 但小于2.容易看出,当 ε 越来越小时,山路或海岸线的长度越来越长.特别地,当 ε →0 时,山路或海岸线的长度也变成无限长.
当时,混沌时间序列分析的基本框架也已完善.给定一个时间序列x(1),x(2),···,x(n),首先需构造一个相空间,其中的向量为

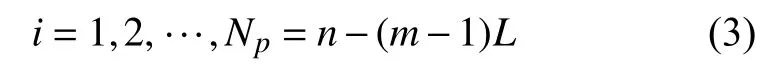
其中,m称作嵌入维,L是延迟时间.然后,可以用Wolf 等[13]的算法计算最大Lyapunov 指数,并用Procaccia 和Grassberger[14]的算法计算关联维(计盒维数D的一个很紧凑的下限)和关联熵(λ1的一个很好估计).一般假设,当关联维为非整数、Lyapunov 指数和关联熵为正时,所研究的时间序列是混沌的.当我们研究圆柱尾流有无混沌现象时,也用到了这个假设[15].但是这样做是不对的.有诸多原因.其一是,用Wolf 等[13]的算法计算最大Lyapunov指数时,小扰动的指数增长特性,只是被假设,但没被证明.事实上可以证明,从任意一组随机的数据,都可以计算出一个正的Lyapunov 指数.一方面,这与混沌来自决定性系统这个原理完全不一致.另一方面,这并不表示随机系统里小扰动有指数发散的特征.事实上,证明一个复杂时间序列的小扰动有指数发散的特征,是一个极富挑战性的问题.第二个原因是,一类很常见的随机过程,1/fα过程,也拥有非整数的关联维和正的关联熵,因而会被误判成混沌[16-17].第三个重大原因是,实验数据总有噪声.当时的分析方法没法帮助研究者撇开噪声,把数据里最重要的特性刻画出来.第四个原因是技术上而非原理性的:实验数据长度有限,因此式(3) 里m和L的选择就变得很重要.这个问题被称作相空间的最优重构.1993 至1994 年间,我和郑先生发表了三篇文章,把这些问题都解决了.下面解释一下基本原理.我们从相空间的最优重构讲起.
从原理上来说,式(3) 里的m只要够大就行,L可以任意.m够大指的是不小于2 倍的计盒维数D[18].问题在于D需要估计而非已知.所以相空间的最优重构这个问题,本质上是在数据有限这个约束条件下,估计最小可用的嵌入维m,然后选择L使得动力学的演化能被最清楚地观察到.m不能太小,可以通过考虑将南北极投影到赤道来理解-在2 维的赤道上,没法区分南北极,所以重构的相空间必须够大,使得地球看起来确实像个地球.L的选择与相空间里运动的速率有关-若速率变化忽大忽小非常极端,则动力学的演化很难被观察清楚.当时已有一个很好的方法,假的最近邻(false nearest neighbor)方法,来最优地重构相空间[19-20].这是一个几何的方法,其基本想法是,当m增大至最小可用的嵌入维时,假的最近邻的个数会急剧减少.嵌入维选定后,延迟时间可以通过让假的最近邻个数最小而得到.
我和郑先生构造的方法是动态的[21-23].基本想法是假定最近邻通过动态迭代后的发散远快于真的最近邻的发散.用方程表述是
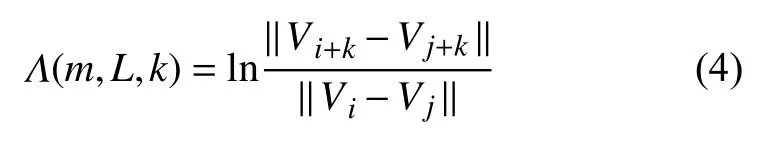
其中,Vi和Vj等是重构的向量,k是演化时间,尖括号表示满足下述条件的所有可能的 (Vi,Vj) 对的系综平均

其中,εk和 Δ εk是任意选择的小距离.这里的每一个不等式对应一个球壳,引入球壳的根本作用是为了刻画噪声的影响.这一点在后面讨论混沌的直接动力学判据时,会更清楚.为最优地决定m和L,可以固定k至一个较小的值.以Rossler 吸引子的重构为例,见图1,我们发现,m=3,L=8 是一个优化解.更多的细节请见文献[21].

图1 Rossler 吸引子的重构Fig.1 Reconstruction of Rossler's attractor
值得指出,这个动态的方法和假的最近邻法,当时是,现在仍是解决相空间重构的两个最系统的方法.我们的动态方法提供更多的信息.以Lorenz 吸引子Lyapunov 指数的估计为例,见图2.当向量对(Vi,Vj)无所限制,即下面不等式(6)里的w为1 时,Λ(k)随时间变化的斜率比Lyapunov 指数小.原因是,对应Lyapunov 指数为0 的轨道上的切向运动也被计算在里边了.让w大一些,如选取54,则 Λ (k) 随时间的变化的斜率与最大Lyapunov 指数完全一致

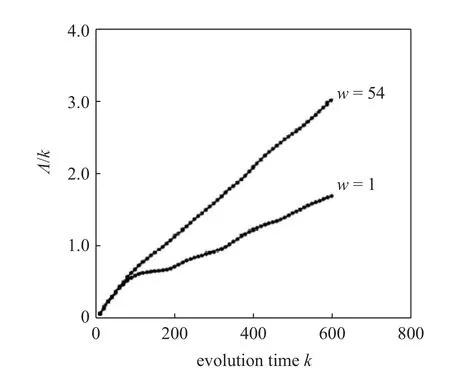
图2 Lorenz 吸引子Lyapunov 指数的估计Fig.2 Estimation of the Lyapunov exponent for the Lorenz attractor
更重要的是,这个动态的方法给出了一个混沌的非常可靠的直接动力学判据.如图3(a)所示,对真正的混沌系统来说,来自不同球壳的随时间变化的指数曲线会形成一个包络线,其斜率给出最大Lyapunov 指数的一个非常好的估计.对随机数来说,如图3(b)所示,来自不同球壳的随时间变化的指数曲线,虽然都能给出一个正的Lyapunov 指数(相当于L(k)/k),但因为是分散的,用不同的球壳去估计最大Lyapunov 指数时,得到的结果都不一样.这是随机系统的本质特征.特别地,当数据集的大小趋向于无限,而球壳的大小趋向于0 时,最大Lyapunov 指数将变得无限大.这也是随机系统的一个根本特征——熵无限大的一个很好的体现.
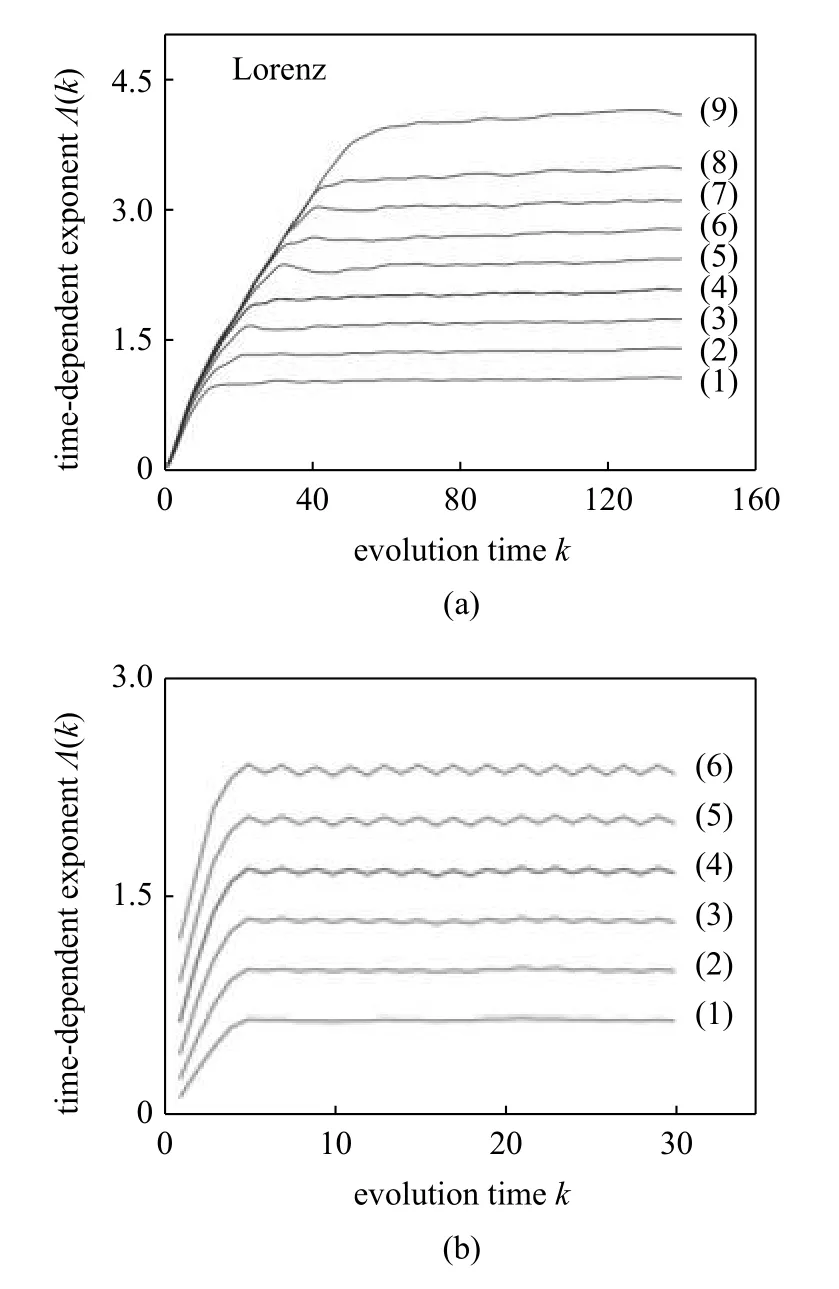
图3 随时间变化的指数曲线作为混沌的直接动力学判据:(a) Lorenz 系统,(b) 随机系统.数字从小到大对应球壳从大到小[21]Fig.3 Time-dependent exponent curves for the chaotic:(a) Lorenz data and (b) IID random variables,where the curves,from bottom up,correspond to shells from larger to smaller[21]
有了这个混沌的直接动力学判据,我们可以搞清楚圆柱近尾流低雷诺数的流动是否有混沌运动[24].图4(a)显示的是Re=136 时的相图.类似的相图在文献里经常出现,如有节律的化学反应和原子力显微镜[25],且被当作混沌运动存在的证据.这里,小扰动以幂律而非指数方式增长,l nεt~t1/2,见图4(b),所以这是极限环上的布朗运动而不是混沌运动.

图4 圆柱近尾流低雷诺数(Re=136)流动的混沌行为:(a) 相图,(b)lnt=ln||Vi+k-Vj+k||随时间的变化[24]Fig.4 Test of chaotic behavior in the near wake cylinder of low Reynolds number (Re=136):(a) phase diagram and (b) temporal evolution of l nt=ln||Vi+k-Vj+k|| [24]
懂了混沌的直接动力学判据后,就能很方便地理解噪声对动力系统的影响.对混沌系统来说,噪声的作用是破坏图3(a)所示的包络线,随着噪声越来越大,包络线从上到下,对应球壳从小到大,将逐渐被破坏,直至包络线完全消失,系统小扰动的指数发散特征不再能被分辨出来.这个现象可以用来估计噪声的大小[26].总的来说,这套方法能非常好地刻画噪声对动力系统,包括半导体激光系统的动力学的影响[27],也能非常好地研究一个相反的问题——噪声引发的混沌[28-30].细节就不再赘述了.这里只强调一下,这也是我在上一节提到的,能在没有任何基础的情况下,简单融入刘教授的团队,研究用半导体激光做混沌安全通讯的原因.
3 基于依赖指数的李雅普诺夫指数(SDLE)的多尺度分析
混沌理论对20 世纪科学思想的最大冲击是,随机性可以不由无限维的随机系统产生,而由有限维的确定性系统产生.这个将随机系统与确定性系统对立的表述,产生的一个很严重的后果是,早期的一些研究者,包括我自己,在选择了混沌研究后,会忽略随机系统的研究.1997 年在UCLA 的电子工程系研究互联网上的交通流时,我意识到这个偏见很糟糕.任一时间、任一地点的互联网牵涉到的用户数,都远多于地面交通牵涉到的车辆数.所以正常情况下互联网上的交通流必然是随机的,这种情况是相对于网络受攻击时的状态而言,当网络受攻击时,其上的交通流会有一个成分,由程序(即规则)产生,因此会不再是完全随机的.互联网上交通流的一个基本特征是长程相关性[31].虽然离散的混沌映射能模拟这个特征[32],但两个著名的随机分形模型,1/fα过程和乘法级联多分形模型,能更全面地模拟互联网上交通流的特征[33-36].值得注意,乘法级联多分形模型是为理解湍流而被发展起来的[37-41],且至今仍是湍流最好的模型之一.早期复杂性科学研究的一大目标是用低维混沌理论研究湍流.所以这里一个深刻的问题是如何将低维混沌与随机分形理论有机地结合起来.SDLE 是为了实现这个目标的一个很有成效的尝试.为了充分理解SDLE 的涵义,下面先介绍一下 1/fα过程.随机系统的其他主要模型,包括ARIMA 模型,Levy 过程,和乘法级联多分形模型,就不在此赘述了(可见文献[1]).
在表征复杂系统的活动类型中,一类非常普遍且令人费解的行为是 1/fα过程,其功率谱密度随频率(时域)或波长(空间域)以幂律方式衰减[1],因此其维数不能通过主成分分析等方法来有效降低[42].这种过程的一个子类,通常表示为 1/f2H+1过程,具有长程相关性,其中,H称作赫斯特指数(Hurst Parameter).取决于 0< H <1/2,H=1/2,或 1/2 < H <1,它们分别被称作具有反持久相关性、无记忆或仅短程相关性,及持久长程相关性(长记忆)[43].此类过程的突出例子包括视觉[44]、金融[45-46]、DNA 序列[47-51]、人类认知[52]、全球恐怖主义[53]、协调[54]、姿势[55-56]、心脏动力学[57-61]以及素数的分布[62]等.
具有长记忆过程的精确定义如下:均值为 μ、方差为 σ2,且协方差平稳的随机过程X={X(t),t=0,1,2,···},当其自相关函数r(w),w≥0 以幂律方式衰减时[63]

则有长程相关性,其中 0 <H< 1.当 1/2 <H<1,这是为什么这种过程被称作具有长记忆.过程X的功率谱密度 (PSD) 为它的积分被称为随机游走过程,其PSD 为作为1/f过程,它们不能被马尔可夫过程或ARIMA 模型恰当地建模[64],因为这些过程的 PSD 与1/f明显不同.为了充分模拟1/f过程,必须使用分数阶过程.最流行的模型是分数布朗运动模型[43].
值得强调的是,充分发展的湍流的Kolmogorov 能谱对应H=1/3,其效应在用雷达观察到的海平面的海杂波上也有反映[65-66].
在上述基础,我们可以讨论SDLE.
假设一个适当的相空间已经重构好了,我们考虑一个轨迹的集合.将两个相邻轨迹之间的初始分离表示为 ε0,它们在时刻t和t+Δt的平均距离为εt和 εt+Δt.相空间中轨迹分离的一个示意如图5 所示.我们考察 εt和 εt+Δt的关系.当 Δt→0,我们有

图5 相空间中轨迹分离的示意图Fig.5 Schematic of evolution of separation of trajectories in phase space
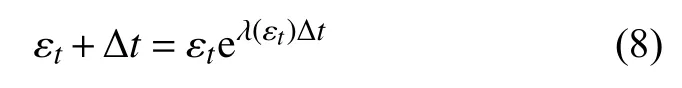
其中,λ (εt) 就是 SDLE,由下式给出

也可以把它表示成一个微分方程

有趣的是,λ (εt) 的计算,完全可以借用上一节描述的我和郑先生发展的方法.具体是,还是基于不等式(5)描述的球壳,我们直接得到
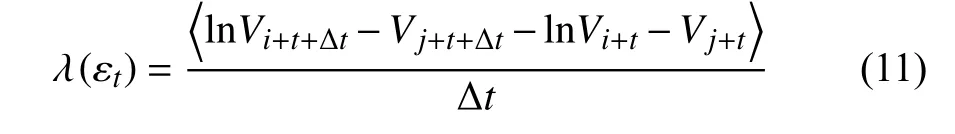
其中,t和 Δt是采样时间的整数倍,尖括号表示球壳内所有下标为i,j的平均值.注意,SDLE 蕴含Lyapunov 指数的概念,但比后者的概念宽广,因SDLE 是一个函数,而Lyapunov 指数只是一个数.
粗略地说,当时我和郑先生发展的方法可以称作是一个积分的形式,SDLE 的表述的是一个微分的形式.由积分形式转至微分形式带来的好处是,在SDLE 的框架下,对所有已知的时间序列模型,我们都可以证明它们有其独特的标度律.下面列举一些,更多的细节请见文献[1,61-67].
性质1:对确定性混沌,可以证明,在小尺度上

性质2:对于有噪声的混沌和噪声引起的混沌,在小尺度上,有

其中 γ >0 决定信息衰减的速率;
性质3:对1/f2H+1过程,可以证明

性质4:对 α-stable Levy 过程,可以证明

性质5:对随机振动来说,依赖于相空间的重构,λ(ε)≈-γlnε 和 λ (ε)≈-Hε-1/H都可被观察到;
性质6:对于具有多尺度行为的复杂运动,上述不同的标度律有可能在不同的 ε 范围内都被观察到.
上述6 个性质,涵盖了几乎所有已知的时间序列模型.因而我们可以期望,SDLE 能统一所有已知的复杂性的度量.事实上也确实如此.比如在刻画脑电动力学时,我们发现,常用的复杂性的度量,包括Lyapunov 指数,关联维,关联熵,赫斯特指数,等都可以被对应到SDLE 在某个尺度的值.细节请见文献[1](15.7.1 节)和文献[68].因这个原因,SDLE 在临床脑电的分析中有极大的应用前景[69].
因性质6 有重大意义,我们用一个例子使其具体化.考察一个动力系统
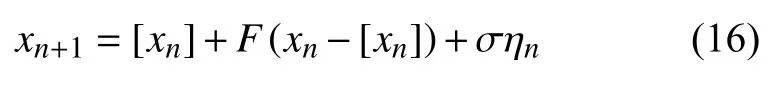
其中,[xn] 表示xn的整数部分,ηn是在区间 [-1,1] 上均匀分布的随机数,σ 刻画噪声的强度,F(y) 是个由下述方程给出的函数
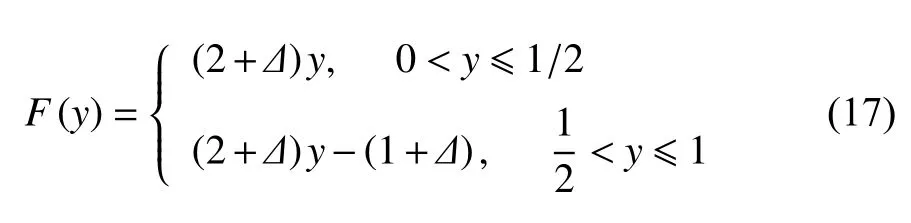
函数F(y) 描述的是一个混沌动力学,其Lyapunov指数为 l n(2+Δ).所以,由方程(16)描述的动力系统是一个整数格点上的随机运动加上整数格点内的混沌运动.因此,当没有噪声时,我们应该在小尺度上观察到性质1,而在较大尺度上观察到性质3.确实如此,如图6 所示.当有噪声时,性质1 被性质2 替代.这里,图6(a)用了5000 点,图6(b)用了500 点.后一种情形,因点太少,整数格点上的布朗运动没能被刻画好(事实上,真正牵涉整数格点的个数只有几十).总的来说,用这么少的点刻画这么丰富的动力学,很令人惊讶.

图6 小尺度上的混沌运动与大尺度上的布朗运动Fig.6 Chaotic motion on small scales and Brownian motion on large scales
性质6 的一个直接后果是,我们可以把一个混沌或分形时间序列拆成很多段,中间插入周期性运动,则原来的混沌或分形特征还是能被SDLE 很好地刻画出来.事实上,前者对应间歇性混沌.一个例子由图7 给出.分形+振荡是长时间监测的心跳动力学的一个基本特征.这里,振荡由呼吸引起.这样的分形很难被SDLE 以外的任何方法刻画.细节就不再此赘述了,请见文献[61].

图7 (a) 由Logistic 映射 xn+1=axn (1-xn) 生成的间歇性混沌时间序列,a=3.8284.(b) 由10000个点的时间序列计算出的 SDLE 曲线,m=4,L=1,最大的球壳尺寸为 (2 -13.5,2 -13).由箭头 A 指示的混沌标度区清晰可见.箭头 B 和 C 表示的区域对应周期性运动和混沌运动之间的过渡,箭头 D 表示大尺度的振荡运动Fig.7 (a) Intermittent chaos generated by Logistic map xn+1=axn (1-xn),a=3.8284.(b) SDLE curve calculated from a time series of 10000 points,m=4,L=1,and the largest shell is (2 -13.5,2 -13).The chaotic scale region indicated by arrow A is clearly visible.The regions represented by arrows B and C correspond to the transition between periodic and chaotic motions,while arrow D represents large-scale oscillatory motion
思考一下,我们就能够明白,SDLE 的提出,拓展了传统混沌动力学的研究范畴,因后者一般只研究由不变测度刻画的含有混沌吸引子的动力系统.在大数据时代,数据一般都是被连续观察的.真正让人激动的数据是那些含有状态突变的数据.这种情形,虽不易由大多数已知的方法来处理,但对SDLE 并没造成任何挑战.这里,值得提一下河流径流动力学.许多研究者猜测河流动力学是混沌的,但分析结果不能让人信服.原因是,河流动力学是强间隙性的—旱季的枯水期和雨季的丰水期,其动力学是完全不一样的.因此,河流的流动形态中若存在混沌,该混沌必须是间隙性的.所幸,这里的混沌很容易通过SDLE 刻画.一个例子如图8 所示.

图8 美国Colorado 河的间隙性混沌.这里,红色的曲线代表由下节的非线性自适应滤波器处理过的数据Fig.8 Intermittent chaos in the Colorado River,USA.Here,the red curves represent the data processed by the nonlinear adaptive filter to be explained in the next section
4 自适应去趋势、去噪、多尺度分解和分形分析
2006 年,美国因在伊拉克和阿富汗缺兵力,由陆军研究部负责,请一家公司设计了一款能用于野外很方便采集脑电的头盔,然后请杜克大学医学院的一个团队采集了一组脑电,最后找到我们,希望我们能设计出一套通过脑电分析,评估受炮弹冲击波冲击而脑震荡的士兵,是否已恢复可以再上前线了.因这个经费来之不易,我们做的非常认真.做了几个月,发现实验得到的脑电信号,其实没有任何真正脑电的信息.但我们不能就这样告诉陆军研究部.所以我们设计了一个新的分析方法,证明给我们的脑电,只有头部摇晃的信号,加上电源60 Hz 的信号(中国是50 Hz),及一些噪音.陆军研究部虽然对我们的分析很满意,但毕竟很失望,因为设计的头盔完全无效.我自己得到的一个深刻体会是,实验数据采集的团队,必须包含能做分析的人员,不然采集的数据可能都是垃圾.
我们的方法是这样的[70-75].先把一个时间序列分成长度为奇数w=2n+1 的小段,相邻两段重叠n+1个点.这样做引入了一个时间尺度=(n+1)τ,其中 τ 为采用时间间隔.对于每一段,我们拟合一个M阶的最佳多项式.请注意,M=0 和 1 分别对应于分段常数和分段线性拟合.分别用yi(l1) 和yi+1(l2)表示拟合的第i段和第(i+1)段的多项式,其中l1,l2=1,2,···,2n+1.注意最后一段的长度可能小于2n+1.我们将重叠区域的拟合定义为

其中,w1=1-(l-1)/n,w2=(l-1)/n可以重写为1-dj/n,j=1,2,其中dj表示那一点与y(i) 和y(i+1)的中心的距离.这意味着权重随点和线段中心之间的距离线性减小.这种加权确保了对称性并有效地消除了相邻段边界周围的任何跳跃或不连续性.实际上,该方案确保拟合处处连续,在非边界点处光滑,在边界处具有右导数和左导数.该方法能有效找出任何一种信号的趋势,假如存在的话.
回到杜克大学的脑电数据.两个例子如图9 所示.红色的曲线由我们的自适应滤波器得到.它们对应头部的晃动.较细的黑色趋势线由另一个很有名的滤波器Loess[76]得到.Loess 等价于Savitzky-Golay 滤波器[77].可以看出,红色的趋势线比黑色的更精确.
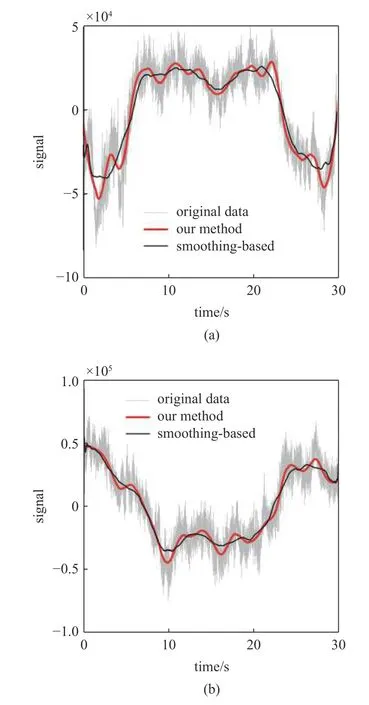
图9 脑电因头部晃动引起的趋势Fig.9 Trend of EEG caused by head shaking
值得比较这个滤波器与前面提到EMD[2].图10(a)显示的是全球年海表温度 (SST)及线性、抛物线、非线性拟合,右边显示的是相应的残差序列.图10(b)与文献[2]的结果完全一致.值得注意,EMD 是个二分法,时间尺度每次减半.这里的自适应算法牵涉到的时间尺度是连续的,因此,在许多应用场合,自适应算法应该比EMD 更准确.
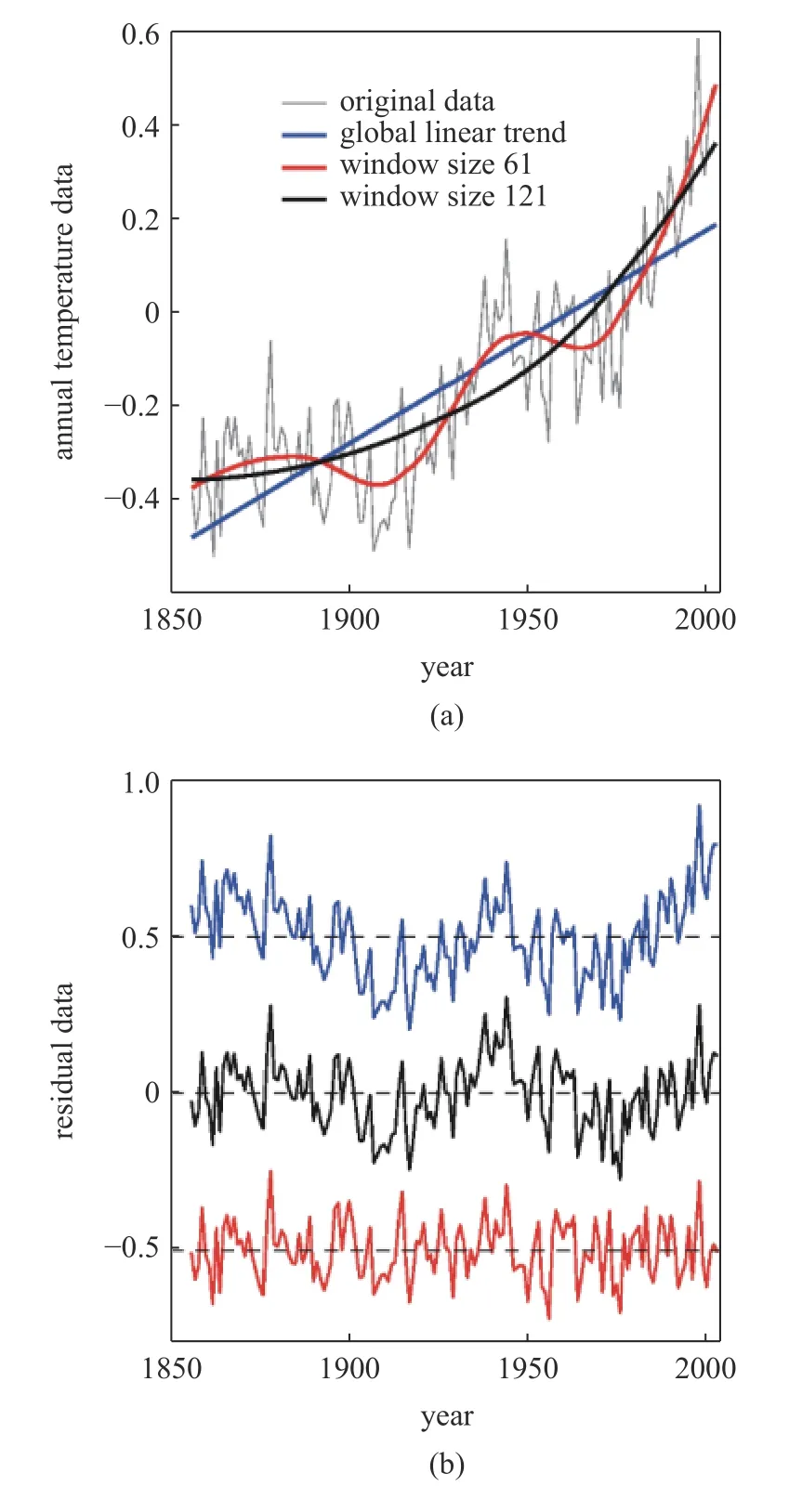
图10 (a)全球年海表温度(SST)及线性、抛物线、非线性拟合和(b)相应的残差序列Fig.10 (a) Global annual sea surface temperature (SST) and linear,parabolic and nonlinear fitting and (b) corresponding residual series
自适应滤波器有非常好的去噪功能.一个例子如图11 所示.可以看出,自适应滤波器比基于混沌的方法和小波变换都好.细节请见文献[71].
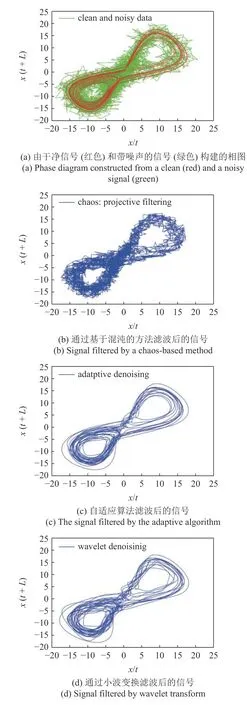
图11 混沌洛伦兹信号的去噪Fig.11 Denoising of a chaotic Lorenz signal
自适应滤波器也有极好的信号提取功能.一个例子如图12 所示.其中,图12(a)和12(b) 是以采样频率为250 Hz 采集的 EEG 和 ECG 信号;图12(c)和12(d)是通过使用自适应和小波变换从 EEG 中提取的ECG 成分.图12(a)中的箭头突出显示了 EEG信号中包含的 ECG 分量.在呼吸综合征的监测和治疗中,脑电EEG 的分析起到很重要的作用.但混杂了心电ECG 成分的脑电,使得通过分析判断是否有呼吸综合征变得很困难.因此,一个重要步骤是先去掉心电ECG 的成分.如图所示,自适应方法比小波变换更优.
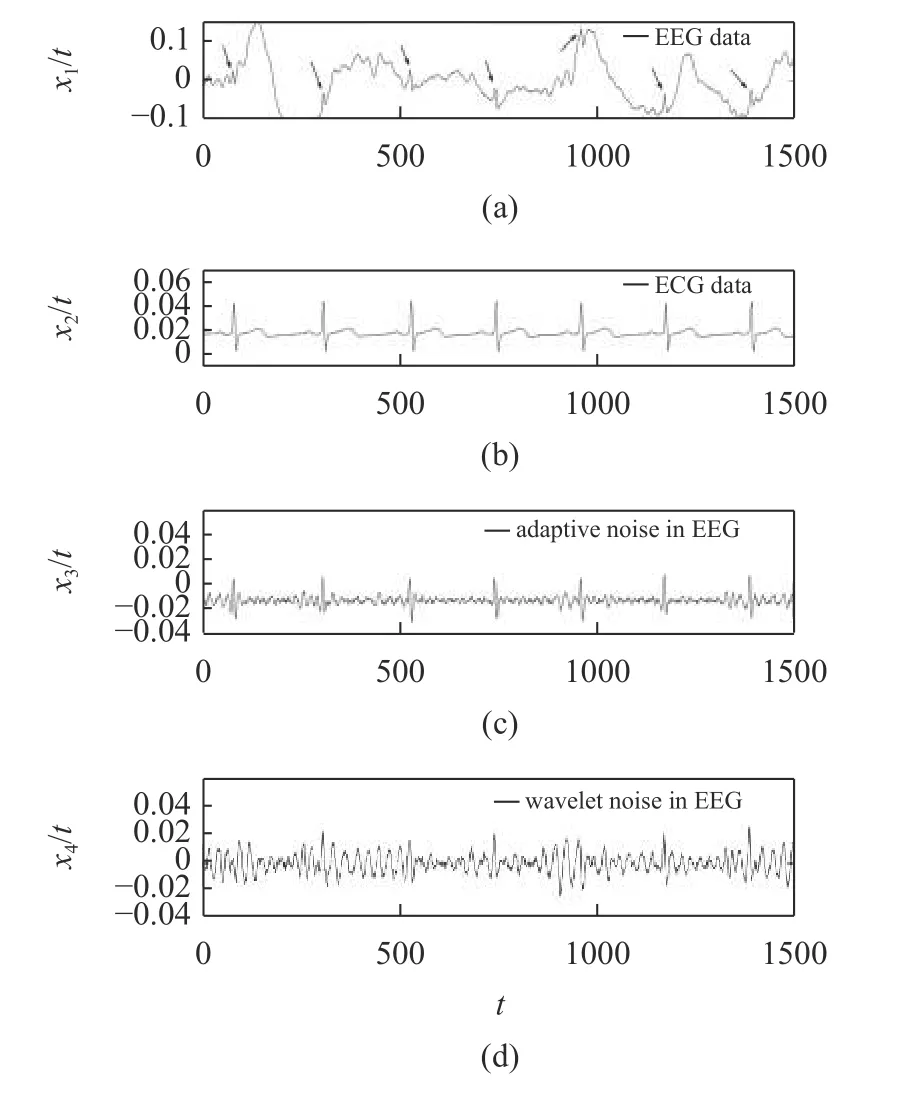
图12 (a,b)以采样频率为250 Hz 采集的 EEG 和 ECG 信号,单位为mV;(c,d)使用自适应和小波变换从 EEG 中提取的ECG 成分.(a)中的箭头突出显示 EEG 信号中包含的 ECG 分量Fig.12 (a,b) EEG and ECG signals acquired at a sampling frequency of 250 Hz in mV;(c,d) ECG components extracted from EEG using adaptive and wavelet transforms.Arrows in (a) highlight ECG components included in the EEG signal
理解了自适应滤波器上述功能后,就很容易理解它的多尺度分解的功能.这相当于用一系列窗口w1,w2,...,wk,得到一连串趋势线,任意两个趋势线的差,都代表原来时间序列在对应那两个窗口的频段的成分.对具体例子感兴趣的,请见文献[73].
最后,我们解释如何用自适应滤波器作分形和多分形分析.事实上,当数据有趋势时,它是所有估计赫斯特指数及广义的赫斯特指数谱的方法中最好的.这里只给出一些最基本的结果.细节请见文献[73].

然后,我们用窗口大小为w对u(n) 拟合一个全局趋势v(n).残差u(i)-v(i) 表征围绕全局趋势的波动,其方差是赫斯特指数H的一个非常好的估计

将上式的平方与开根号稍作变化,我们就得到估计广义的赫斯特指数谱的多分形分析
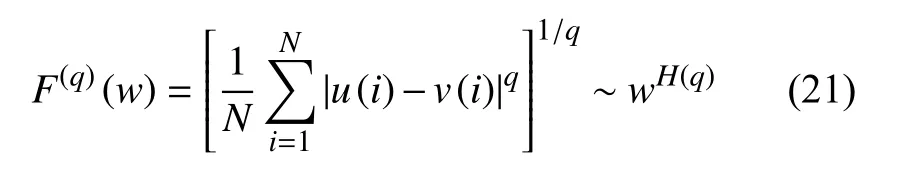
将式(20)应用于两个随机游走过程u(n) 和z(n),我们可以计算它们间互相关的长程相关指数Huz
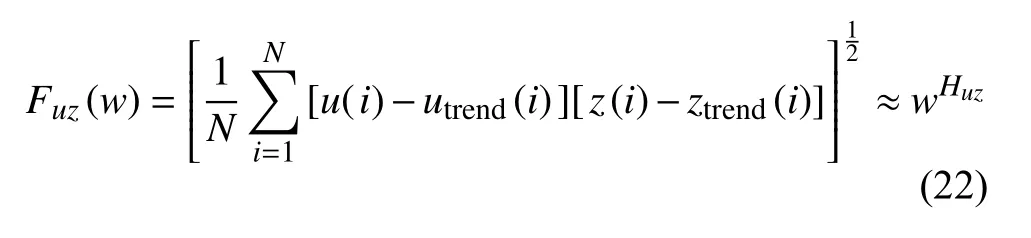
图13(a)显示的是一个典型的脑电信号的分形分析结果.从中我们可以定义三个参数,短时间和长时间的赫斯特指数(记为HS和HL),及饱和度(saturation level),就可以把三类脑电数据,正常(Group H),癫痫发作(Group S),癫痫病人未发作(Group E),几乎完全区分开.近期,我们发现这个方法有很大的临床应用前景[78].
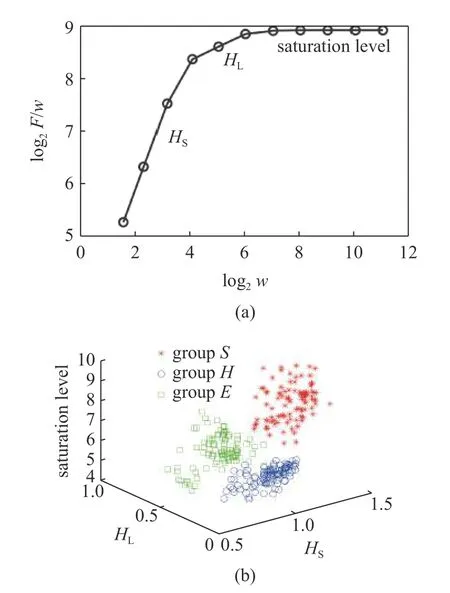
图13 (a)一个典型脑电信号的分形分析结果;(b) 三类数据,正常(Group H)、癫痫发作(Group S)、癫痫病人未发作(Group E)的分类,精度几乎100%Fig.13 (a) Typical adaptive fractal analysis of a an EEG signal;(b)Classification of three types of EEG data,normal (Group H),seizures(Group S),and seizure patients not having seizure (Group E),with an accuracy of almost 100%
5 结语
5 G 时代的到来及 6 G 时代的快速临近,科学、工程和社会中积累的大数据将很快变得更加巨大.任何人都不得不抓住这个前所未有的机会.虽然计算机科学家们正在努力开发更强大的数据库管理和机器学习方法,但现在是进入下一阶段的时候了.这个阶段将以捕获大数据背后的动力学及深刻理解人脑的工作机制为基本目的.就数据分析而言,我们可以洞见,机器学习和复杂性科学的主流方法在未来会相互补充并互相促进.为了帮助加速这个结合,我们提倡协同使用基于主流机器学习的方法和复杂性科学中的多尺度方法.
最后我们强调,在科学研究中,最重要的是一直保有一颗好奇、不断探索的心.只有这样,才能发现真正重大的科学问题并切实解决实际问题.这种普世的精神,郑先生等老一辈科学家们一直在言传身教.望读者们能和我们共勉!
