基于FTA的齿轮与轴过盈联接失效影响参数分析＊

龚青山 徐 昊 郭庆贺 吕 江 曹占龙

（①湖北汽车工业学院机械工程学院，湖北 十堰 442000；②东风汽车有限公司刃量具厂，湖北 十堰 442000）

过盈联接结构简单，无需使用螺钉、键或销等其他紧固件来联接，可避免因附加紧固件引起的应力集中问题，且承载能力高、定心精度好，广泛应用于齿轮与轴之间的联接[1]。齿轮和轴过盈联接的可靠性受诸多因素影响，找出过盈联接失效的关键影响因素并合理地设计各个影响参数，对增加过盈联接可靠性尤为重要。

近年来，国内外学者针对过盈联接可靠性问题进行了一定的研究并取得了一些研究成果。孙玲芳[2]使用Abaqus对机车轮对进行有限元建模，针对不同的装配过程分析了空心度和过盈量对应力的影响，优化出合理的空心度和过盈量范围。Paredes M[3]用有限元法对过盈联接紧固件进行了研究，讨论了过盈量和摩擦因数对轴向载荷损失的影响，找到了轴向压力及其载荷损失的变化规律。王挺等[4]研究了齿轮和轴因压装不当而产生轮轴接触面剧烈受损的问题。周鹤群等[5]人采用有限元法对传动轴过盈联接进行了精确分析，把传动轴和厚壁圆柱过盈装配进行理论计算并分析了离心力对过盈配合的影响。邹渊等[6]人研究了过盈联接时齿轮和预应力的关系，最终得出了齿轮内径、过盈量和预应力三者的关系式。Oswald F B等[7]研究了过盈联接对轴承寿命的影响。张金煜等[8]通过对高速动车组轮对压装过程的仿真，探讨了压装过程中轮轴的应力、应变及变形特征。杨广雪等[9]建立了过盈配合的微动损伤有限元模型，分析了不同参数对过盈联接微动损伤的影响。但对于齿轮与轴过盈联接失效问题研究较少，且目前大多数过盈参数仍使用经验法来设计，缺乏可靠的检验及设计工具。因此，探究一种质量工具来科学设置过盈参数对提高轮轴过盈联接可靠性意义重大。

针对齿轮与轴过盈联接发生的齿轮断裂失效问题，拟采用故障树分析法（fault tree analysis, FTA）这一质量工具来建立齿轮轴过盈联接系统故障树，找出影响齿轮断裂失效的主要影响因素，并分析各影响因素对齿轮轴过盈接触时Von Mises应力的影响规律，为齿轮轴过盈联接时发生齿轮断裂失效问题诊断和预防提供理论支撑。

1 轮轴过盈联接问题描述及计算

1.1 轮轴过盈装配应力及位移的理论计算

当齿轮与轴过盈装配时，由于齿轮与轴之间存在过盈量，导致齿轮的内径扩大，轴的外径被挤压缩小，过盈接触面会产生垂直向上的正压力，进而在轮轴接触面产生摩擦力来转递扭矩和轴向力。齿轮与轴过盈配合与轴的运动状态有关，当轴低速运转时，离心力对齿轮与轴过盈配合的影响可以忽略不计；但对于高速旋转，离心力对齿轮与轴过盈配合的影响至关重要[10]。因此，齿轮和轴在过盈装配时不仅要满足轴可以传递静态扭矩，而且要考虑轴在动态传动时不会打滑掉载。齿轮和轴之间的过盈配合面简化为如图1所示。

图1 齿轮和轴过盈联接简化模型

齿轮的应力分量和位移为[11]

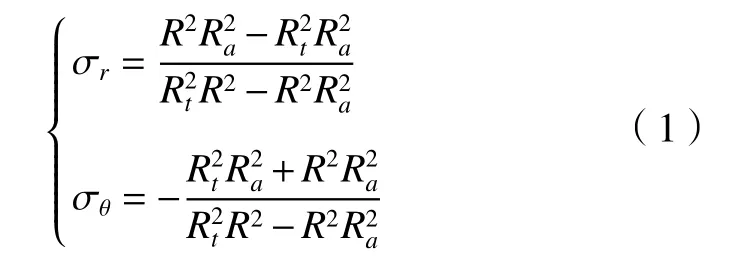
式中： σr为径向应力； σθ为周向应力；Ra为轴的半径；Rt为齿轮齿顶圆半径；R为接触半径到齿顶圆直径之间的任意半径。

记轴任意位置处的径向位移为u，则有

化简可得

式中：E为弹性模量； μ为材料的泊松比；p为过盈配合产生的内应力。

1.2 齿轮轴压装过盈量的确定

1.2.1 最小过盈量计算

能正常传递载荷而不发生掉载所需的最小装配压力为

式中：T为传递转矩；df为结合直径；lf为结合长度；μ为结合面摩擦系数。

齿轮与轴的直径比分别为

式中：qa为齿轮直径比；qi为轴直径比；da为齿轮外径；di为轴内径。

齿轮与轴传输扭矩所需最小直径变化量为

式中：Ea为齿轮的弹性模量；Ei为 轴的弹性模量。

式中：va为齿轮的泊松比；vi为轴的泊松比。

传递载荷所需的最小有效过盈量为

1.2.2 最大过盈量计算

齿轮和轴不发生塑性变形所能承受的最大装配压力为

式中： σsa为 齿轮的屈服强度； σsi为轴的屈服强度。

齿轮与轴未变形所能承受的最大装配压力为

齿轮与轴未变形所能承受的最大直径变化量为

齿轮与轴未变形所能承受的的最大过盈量为

2 齿轮轴过盈联接系统故障树分析

2.1 故障树的建立

故障树分析法是可靠性分析方法中非常重要的分析工具，它通过故障树模型来表达各个影响因素之间的联系。该方法把系统出现的问题放在故障树的最上面，作为其顶事件，然后从顶端到底端逐步分析故障因果逻辑关系，逐层找到系统发生故障的所有因素及各个因素的组合[12]，从而能够有针对性地去解决问题。下面对齿轮与轴的过盈联接系统建立系统故障树模型，对可能引起齿轮断裂失效的所有因素进行全方位分析。齿轮与轴过盈联接失效故障树见图2所示。

图2 齿轮与轴过盈联接失效故障树

2.2 故障树定性分析

故障树的定性分析可以找到导致系统顶事件发生的全部因素，将所有因素及因素组合的最小集合称为最小割集[13]。从顶事件问题开始，遵循从上到下逐步分析的基本原则，或门提高最小割集的个数，与门增大最小割集的容量，一直扩展到所有的基本因素把全部的逻辑门所取代，然后用布尔代数规则得到总的最小值。

式中： T 为齿轮与轴过盈联接失效； X1为工人师傅操作失误； X2为过盈量选取不合理； X3为摩擦因数选取不合理； X4为压装速度不合理； X5为材料型号选择不合理； X6为材料加工工艺误差； X7为轮轴接触面形状误差； X8为齿轮与轴装配偏差； X9为齿轮厂家生产质量缺陷； X10为传递最大扭矩误差。

2.3 故障树定量分析

故障树的定量分析通常采用独立事件的概率公式来计算顶事件发生的概率。假设用A和B来代表成功事件，则故障树系统中的OR门（如图3所示）实际上表示的是所有成功事件的集合[14]。两事件或门故障树结构的概率关系为

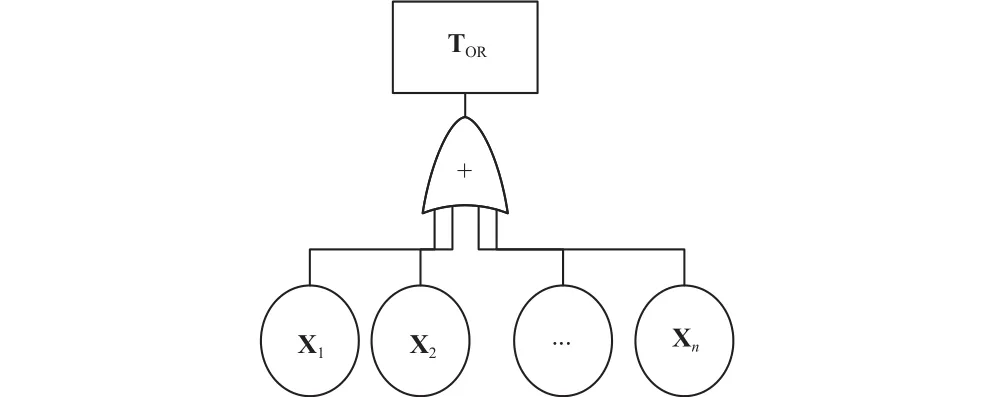
图3 或门故障树

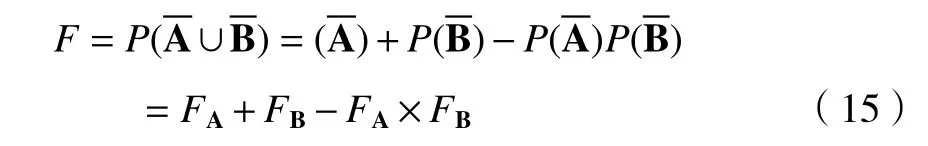
或门结构对应的故障树框图如图4所示。

图4 或门故障树框图

事件的逻辑关系式为

如果所有基本事件互不相干，那么输出事件的概率就是所有原因发生概率的总和。

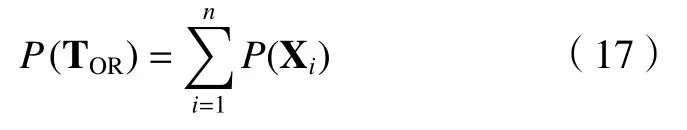
通过对某公司轮轴过盈装配车间现场实际生产数据收集和分析，计算出齿轮轴过盈联接系统故障树底事件的故障概率如表1所示。

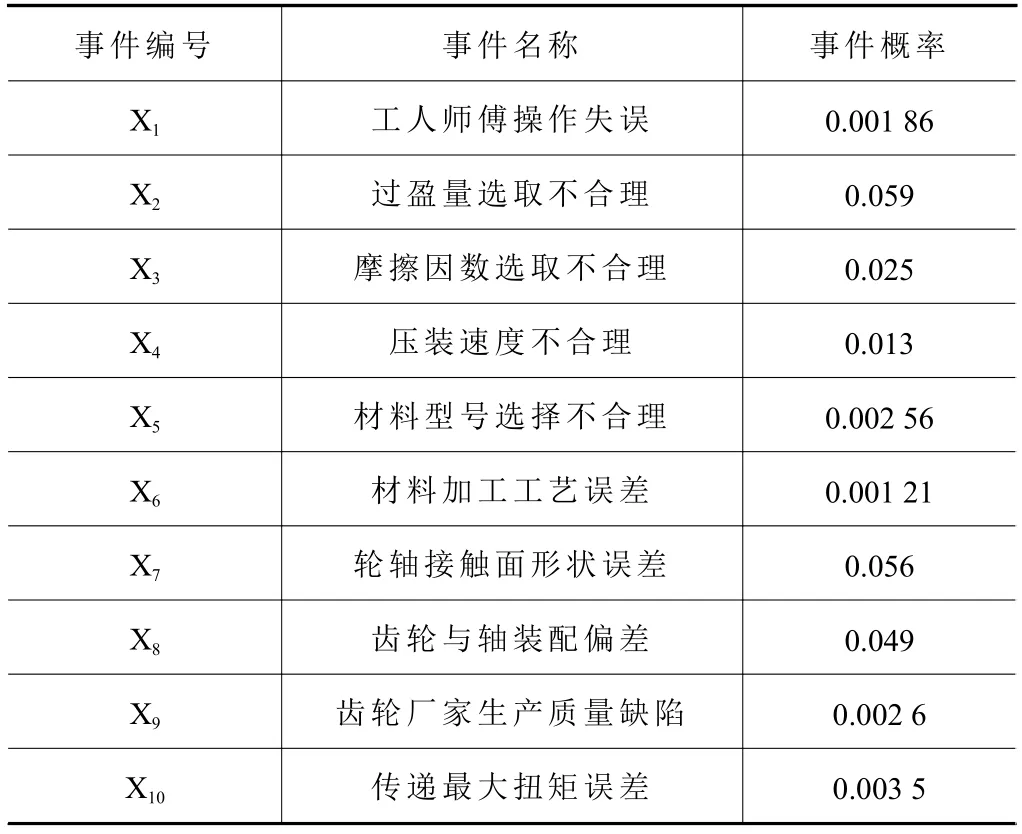
表1 齿轮轴过盈联接系统故障树基本事件概率表

底事件中任何一个事件单独发生，都有可能导致齿轮和轴过盈联接失效，造成齿轮断裂。采用概率公式来计算顶事件齿轮轴过盈联接齿轮断裂失效的概率，如式（18）所示。

式中： φ (T)为顶事件；qi为底事件概率；n为底事件数量。

由式（18）和FreeFta故障树分析软件可以得到，齿轮和轴过盈联接失效故障的顶事件概率为φ(T)=0.03，即每100对齿轮与轴过盈联接大约有3对会发生联接失效问题。

2.4 轮轴过盈联接系统失效各事件重要度分析

齿轮与轴过盈联接系统故障树各底事件对顶事件发生的影响程度不同，所以需要对轮轴过盈联接系统故障树进行重要度分析，找出造成系统发生失效的关键影响因素。齿轮与轴过盈联接系统故障树的重要度分析分为关键重要度分析和概率重要度分析。

关键重要度指底事件概率变化率引起的顶事件概率变化率，它能够反映出事件经过改善以后对系统的影响程度，其计算公式如式（19）所示。

概率重要度表示系统故障树底事件的概率发生变化时对其顶事件的影响程度，计算公式如（20）所示。

式中：PT为顶事件失效率；Pi为底事件失效率。

根据式（19）和式（20）计算齿轮与轴过盈联接系统故障树中底事件的关键重要度和概率重要度。由于建立的齿轮与轴过盈联接系统失效故障树只有串并联，所以概率重要度与关键重要度的趋势一致[15]。故只需要计算关键重要度，如表2所示。

表2 底事件的关键重要度

从表中可以看出：造成顶事件“齿轮轴过盈联接失效”的事件X2“过盈量选取不合理”的关键重要度最高，是结构中的关键环节，故在设计其结构时要特别关注，避免失效造成齿轮压装断裂失效；其次事件X3“摩擦因数选取不合理”、事件X4“压装速度不合理”、事件X7“轮轴接触面形状误差”及事件X8“齿轮与轴装配偏差”关键重要度较高，故为了更好地避免系统过盈联接失效情况的发生，有必要研究过盈量、摩擦因数、压装速度、装配偏差及形状误差对齿轮与轴过盈接触时Von Mises应力的影响规律。

3 齿轮与轴过盈联接案例

下面对某公司变速箱中间轴齿轮过盈联接案例进行分析，其中传递转矩：T=2 500 N·m；齿轮外径：da=99.6 mm，中间轴内径：di=30 mm，结合长度：lf=84.2 mm，结合面摩擦系数μ=0.08，结合直径：df=70.5 mm，弹性模量：E=20 600 N/mm2，泊松比：Va=0.3。将数据代入式（8）和式（13），可得出过盈量范围 δe=0.073～0.527 mm。然后采用ANSYS Workbench对齿轮与轴过盈联接系统进行瞬态动力学分析，讨论了过盈量、摩擦因数、压装速度、装配偏差及形状误差对齿轮轴过盈接触时Von Mises应力的影响规律。变速箱齿轮轴装配总成及齿轮压装断裂失效场景图如图5和图6所示。

图5 变速箱齿轮轴装配总成

图6 齿轮压装断裂失效

3.1 有限元模型建立

有限元仿真计算是在三维实体模型的基础上进行的。结合某变速箱中间轴和齿轮的具体参数，先在三维软件中建立了变速箱内部齿轮及部分中间轴（与其齿轮装配在一起的部分）的三维立体模型，如图7所示，进而将其放入有限元软件中对其进行瞬态动力学研究，在DesignModle界面对其中间轴齿轮系统模型进行简化处理来降低运算量，如去除不必要的倒角。在Mechanical界面中建立有限元模型，采用Solid187单元类型划分网格，如图8所示。大约有280 000个单元和420 000个节点，模型材料采用合金结构钢20MnCr5。创建轮轴接触对时选择有摩擦接触对来更贴合实际工况，同时将中间轴的端面设置全约束，在齿轮的端面施加位移载荷，同时设置两个求解步骤，最终完成对变速箱中间轴齿有限元模型的建立。

图7 齿轮和轴装配实体模型

图8 齿轮和轴装配体网格划分

3.2 过盈量对压装过程的影响

采用改变单一变量的试验方法，控制中间轴齿轮结合面摩擦因数为0.1，系统装压速度为1.5 mm/s不变，忽略轮轴装配偏差和形状误差的影响，依次设置装配过盈量为 0.073 mm、0.310 mm、0.527 mm，探讨系统过盈接触应力随着轮轴压装深度改变的分布情况。在图9中可以清晰地看出Von Mises应力曲线走势规律，影响应力数值主要与轮轴压装过盈量的大小有关。当系统装配盈量设置越大时，Von Mises应力也就越大。总体上来看，应力分布的趋势基本保持一致。

图9 不同过盈量下 Von Mises应力轴向分布情况

控制其他影响因素不变，图10给出了不同过盈量下的中间轴齿轮装配曲线。明显看出，系统装配过盈量与压装力几乎成正比，但对曲线总体变化趋势影响很小。

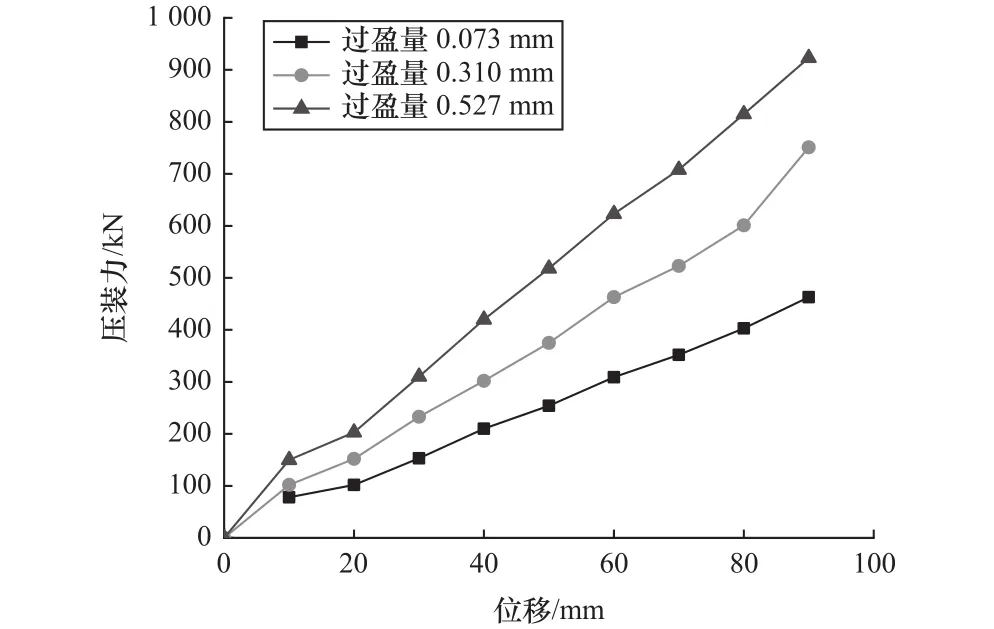
图10 中间轴齿轮装压曲线图

3.3 摩擦因数对压装过程的影响

控制中间轴齿轮系统装配过盈量为0.310 mm，系统装配速度为1.5 mm/s不变，忽略轮轴装配偏差和形状误差的影响，依次选取中间轴齿轮结合面摩擦因数为0.1、0.15、0.2，分析系统结合面Von Mises应力与轮轴压装深度的变化规律。如图11所示中间轴齿轮结合面摩擦因数对Von Mises应力有一定的影响。

图11 不同摩擦因数下 Von Mises应力轴向分布情况

3.4 压装速度对压装过程的影响

控制中间轴齿轮装配过盈量为0.310 mm，系统结合面摩擦因数为0.15不变，忽略轮轴装配偏差和形状误差的影响，选取轮轴装配速度1.5 mm/s和3 mm/s。不同装配速度下轮轴 Von Mises应力的轴向分布曲线如图12所示，2种压入速度下，齿轮轴接触面的Von Mises应力曲线基本完全一致。所以，齿轮压装速度对齿轮轴应力基本没有影响。

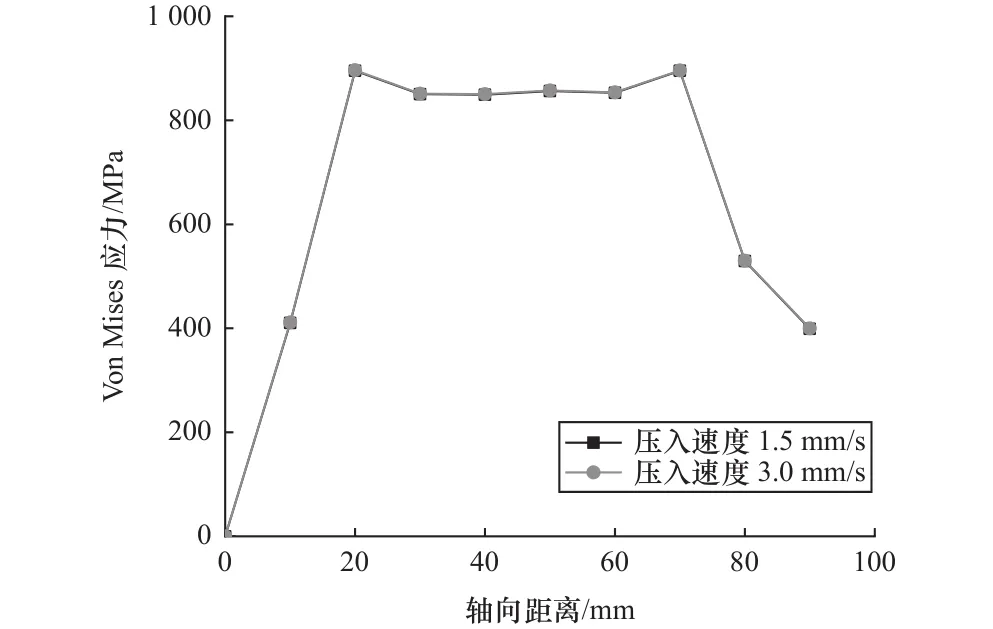
图12 不同压装速度下 Von Mises应力轴向分布情况

3.5 装配偏差对压装过程的影响

控制中间轴齿轮装配过盈量为0.527 mm，系统结合面摩擦因数为0.1，压装速度选取1.5 mm/s不变，忽略轮轴接触面形状误差的影响，针对中间轴与齿轮在压装过程中存在的中间轴位姿偏差进行了分析。中间轴的位姿偏差如图13所示，中间轴的轴线和齿轮孔轴线之间的夹角为θ，依次设置θ为0°、0.10°、0.20°时，探讨系统过盈接触应力随着轮轴压装深度改变的分布情况，结果如图14所示，当夹角θ增大时，轮轴接触Von Mises应力也随之增大，且影响显著。

图13 中间轴位姿偏差

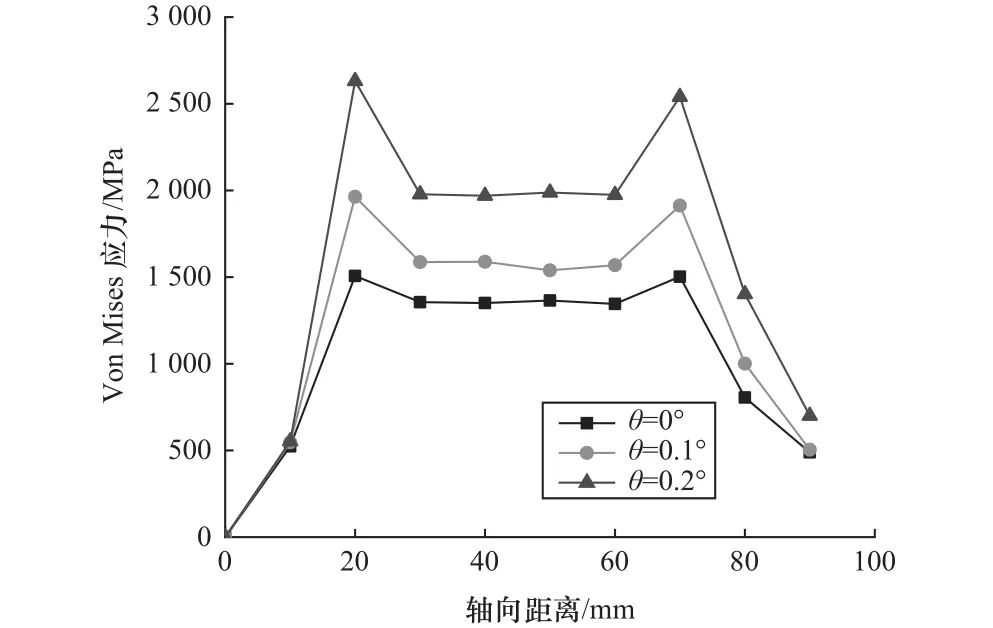
图14 不同装配角度误差下 Von Mises应力轴向分布情况

3.6 形状误差对压装过程的影响

在实际加工过程中，中间轴的外圈可能出现形状误差有3种情况，如图15所示。

图15 中间轴外表面的 3 种形状误差

图中 Δ表示圆柱度数值，e为过盈量。控制轮轴装配过盈量为0.527 mm，系统结合面摩擦因数为0.1，压装速度选取1.5 mm/s，圆柱度数值 Δ为0.2不变，忽略轮轴接触面装配误差的影响，讨论不同形状误差对轮轴接触应力的影响，结果如图16所示，当中间轴存在鼓形、锥形形状误差时，相比理想形状时接触应力明显增大。但当中间轴存在凹形误差时，接触面面积减小，滑动摩擦力将减小，从而轮轴接触应力也将减小。

图16 不同形状误差下 Von Mises应力轴向分布情况

4 结语

通过故障树分析法找出齿轮与轴过盈联接失效的各种影响因素，并对其进行重要度分析找出其关键因素，进而针对这些关键影响因素对齿轮与轴的装配过程进行瞬态动力学分析，模拟齿轮与轴压装的动态过程，通过分析压装过程中压装力和轮轴接触面上Von Mises应力的变化规律，得出以下结论：

（1）齿轮与轴过盈联接系统失效的主要影响因素为过盈量、摩擦因数、压装速度、齿轮与轴的装配偏差以及接触面存在的形状误差。

（2）轮轴接触应力受过盈量、摩擦因数、装配偏差和形状误差影响较大，压装速度对其几乎没有影响，但对应力分布的趋势影响都很小。

（3）采用故障树分析法，建立系统故障树进行综合评判，为轮轴过盈联接失效问题诊断和预防提供了有效的分析途径。