机器人为测量系统的工具坐标系标定方法研究
2022-08-30练少勋南晓萱王杼荣席文明
练少勋 南晓萱 王杼荣 席文明
(厦门大学航空航天学院,福建 厦门 361102)
在自动化制造中,机器人采用示教编程的方法,满足品种单一、高效率的产品制造。而在数字化制造阶段,一方面制造向高精度、复杂结构产品领域发展,另一方面为满足市场中的定制生产,需要快速重组生产系统以及更迅捷的机器人编程技术。通过对机器人系统进行标定,并建立机器人系统的镜像模型-模拟仿真系统,可以有效提高机器人的加工精度,并实现机器人轨迹的软件编程,从而满足高精度、复杂结构产品的定制[1-3]。
机器人系统标定是建立其镜像模型-模拟仿真系统的基础,它包含机器人本体标定和机器人末端工具标定。机器人本体标定通常有4个步骤组成,即理论建模、误差测量、参数计算和轨迹校正[4-7]。所谓理论建模就是建立机器人运动学参数的数学模型,通常有D-H法、MDH法和旋量法等;而误差测量是利用高精度测量仪器测量机器人末端的位姿误差,测量仪器包括三坐标测量机、球杆仪、视觉系统以及激光跟踪仪等;参数计算就是利用第二步的测量误差反求机器人的运动学参数,由于数学模型高度非线性,一般采用最小二乘迭代法、神经网络、卡尔曼滤波器算法求解机器人运动学参数,最后借助求取的机器人运动学参数,利用逆运动学解,在关节空间对机器人进行轨迹校正。机器人末端工具标定主要包括约束标定和非约束标定,所谓约束标定是指机器人(tool center point,TCP)位置不变,通过姿态的变化获取求解工具坐标系位姿参数的方程,通常有四点标定法、六点标定法等[8-9]而非约束标定是利用高精度测量仪器,直接获取工具坐标系相对于机器人基坐标系的位姿[10]。该标定方法类似于机器人的本体标定,都是通过测量工具在空间某些点的位姿误差,利用建立的数学模型反求工具的坐标参数。
标定机器人末端工具的最终目的是建立机器人数字化系统的模拟仿真单元,即利用标定参数建立实际机器人系统的镜像模型。利用机器人系统与机器人数字化系统中的镜像模型一致性,可以有效降低标定难度,提高标定精度。由于工具安装在机器人末端,利用机器人自身无法直接测量工具的坐标参数,所以首先利用机器人作为测量系统建立测量工具的第二基准,然后利用机器人末端工具相对第二基准的位姿在机器人系统与机器人数字化系统中的一致性,实现工具的标定。
1 基于镜像模型的工具标定方法
在标定机器人末端工具前,首先建立机器人模拟仿真系统。使用的是日本安川工业机器人,所以模拟仿真系统采用安川公司的MOTOMANSIMEG软件。图1是实际机器人系统和在模拟仿真软件中建立的数字化机器人系统,在图1中,、分别是实际机器人系统的基坐标系、机器人末端第六轴坐标系、机器人末端工具坐标系和工具顶端的TCP坐标系,分别是数字化机器人系统中的机器人模型基坐标系、末端第六轴坐标系、末端工具坐标系和工具顶端的TCP坐标系。

图1 机器人系统与数字化机器人系统的坐标系设定
如图2所示,为了标定机器人末端工具,首先需要利用标定探针建立第二基准,第二基准是一已知尺寸的长方体。标定时,探针安装于机器人末端代替工具,假设该长方体在实际系统和模拟仿真系统中的坐标系分别为∑XNYNZN、∑xnynzn,标定完成后,其长方体对应棱线平行于机器人基坐标系的对应坐标轴。利用标定参数(长方体相对于机器人基坐标系的位姿关系)调整模拟仿真系统中长方体模型的位姿,建立长方体在数字化机器人系统中的镜像模型。

图2 第二基准建立方法
由两个系统中机器人末端工具与第二基准长方体之间的约束关系,可以得到以下的方程
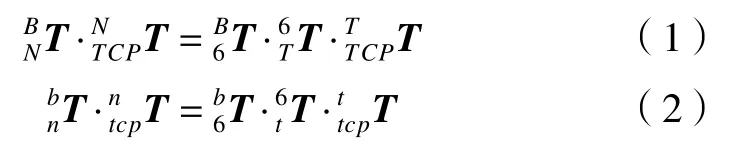

式(3)成立的条件是机器人末端工具制造(与CAD模型尺寸一致)和安装没有误差。
实际上,机器人末端工具在制造和安装时存在误差,导致两个系统中工具相对第二基准的约束关系不一致性,即,使得式(3)不成立。在图3a的实际机器人系统中,工具与长方体上表面平行并接触,将此时机器人的末端位姿参数输入到模拟仿真系统的机器人模型中时,其机器人末端工具模型并不与长方体模型上表面平行且接触,见图3b,说明机器人末端工具在制造和安装时存在位置和姿态误差。为了保持两个空间中工具与长方体约束关系的一致性,即保持,需要将工具模型绕机器人末端第六轴进行平移和旋转,平移和旋转后见图3b虚线所示,即在模拟仿真系统中,机器人末端工具模型也增加与实际机器人末端工具同样的安装与制造误差,这样才能保证模拟仿真系统中的工具模型是实际机器人末端工具的镜像。此时式(3)成立的条件为
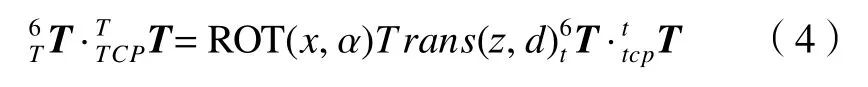
式中:α是在模拟仿真系统中,绕机器人末端第六轴x6旋转的角度;d是沿机器人末端第六轴z6平移的距离。从图3b可以看出,旋转和平移后,工具坐标系与机器人第六轴坐标系产生了分离。

图3 工具镜像模型建立方法
第二基准长方体的不同面和棱边用于调整工具坐标系不同轴的姿态和位置,通过最多不超过沿x6、z6轴的旋转以及沿x6、z6、y6的平移,可以使得两个空间中工具相对于长方体的约束关系一致。所以模拟仿真系统中,工具模型调整的通式为
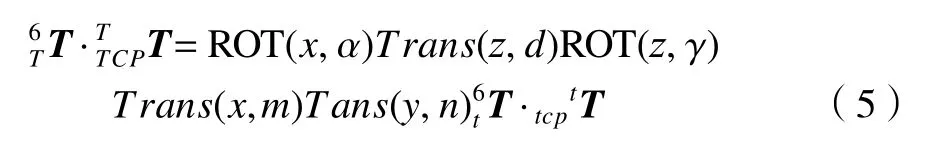
假设图2右图中的长方体为待加工产品毛坯,在CAM软件中产生的刀轨迹为相对于物体坐标系,参照图2右图,假设刀轨迹为∑xoyozo,则∑xnynzn到∑xoyozo的转换矩阵已知。刀轨迹后置处理就是将∑xoyozo从相对∑xnynzn转换到相对于机器人基坐标系∑xbybzb。
在实际机器人空间中,假设对刀点设置在毛坯前表面的中心处,其坐标系为∑XDZDZD,则根据毛坯尺寸,对刀点到毛坯坐标系∑XNYNZN的转换矩阵已知,这样已知,也即在模拟仿真系统中已知,是模拟仿真系统中对刀点到毛坯坐标系的变换矩阵。现在需要求解∑XDZDZD的位置和姿态。
首先求取对刀点的姿态,沿长方形毛坯面取3个点PK、PL、PM(这3个点可以由标定工具后的机器人测量),并且这3个点组成一直角三角形,则可以依据这3个点求得三点所在平面的姿态,即对刀点所在平面的姿态

可以得到

由式(1)可以求得TCP坐标系相对机器人基坐标系的转换矩阵,即

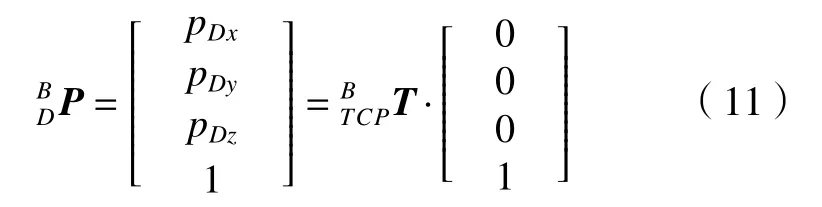
由于模拟仿真系统中的毛胚模型是实际机器人系统中毛胚的镜像,即,则可以利用实际机器人空间求得的对刀点位姿参数,对模拟仿真系统中的毛坯模型进行位姿调整,从而保持毛坯在两个系统中的镜像关系。因为已知,这样由式(9)和式(11)构建,从而将刀轨迹转换到机器人基坐标系中,即
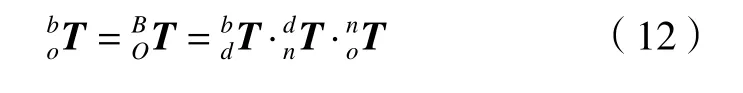
2 实验结果及分析
为了验证本文方法的有效性,利用ArtCAM(英国Delcam公司)软件产生加工刀轨迹。工具标定前将刀轨迹转换成机器人轨迹,该轨迹在180°方向上分别加工雕塑前后面。工具标定后将刀轨迹转换成机器人轨迹,该轨迹在180°方向上分别加工两个半长槽,共加工4组。通过加工雕塑前后面的错开误差以及两个对应半长槽的错开误差,验证机器人末端工具的标定精度。机器人加工系统见图4所示,机器人型号为安川MH250,抓取重量250 kg,工作空间2 700 mm。采用韩国艾彦125TD15Z7.5B电主轴,功率 7.5 kW,最高转速为 18 000 r/min,电主轴由连接块通过法兰与机器人末端法兰连接。

图4 机器人加工系统
图5a为工具标定前雕塑加工的前后面错位误差,图5b为加工一侧半长槽,图5c是工具掉转180°后加工另一侧半长槽,图5d是通过划线,测量两个半长槽的错位误差。雕塑前后面的错开误差(图5a局部图中箭头前后错开的距离)为5.1 mm,4组通槽侧面的错开误差分别为0.68 mm,0.71 mm,0.73 mm 和 0.69 mm。

图5 双侧加工以及测量实验
图6是标定工具后,加工一汉白玉雕塑。该雕塑的毛胚是一个长方体,通过双侧粗加工去除多余材料余量。由于人物头部形状复杂,采用双侧加工无法完整地加工细节,所以头部采用四侧精加工,其余部分采用双侧精加工。图6a是双侧粗加工过程,多余毛胚余量被逐渐切除,人物形状逐渐被加工出来。图6b、图6c是完成双侧粗加工后,双侧加工局部对准情况,可以看出,工具标定后双侧加工对准精确,能够精确加工出人物形状。图6d、图6e是头部四侧精加工效果,通过工具标定,能够将头部复杂的纹理精确地加工出来。

图6 标定工具后产品加工效果
图5、图6都采用了相差180°的双侧加工,每侧加工时工具姿态保持不变,是一种特殊的加工情况。为了获得轨迹姿态连续变化的加工情况,利用实验对一回转体进行加工。首先由PowerMill(英国Delcam公司)软件产生回转加工刀轨迹,然后将其转换成机器人轨迹。由于机器人关节轴运动范围的限制,加工方法是机器人先回转加工0°~180°范围内的回转体,然后调转工具方向,再回转加工180°~360°范围内的回转体,通过两次加工的拼合,完整地加工出回转体。机器人加工时,其工具末端TCP的Z轴垂直回转体模型轴线并绕其旋转。
图7a是机器人系统在回转加工左侧回转体(回转加工是指刀具法向量垂直圆柱表面,从而使得机器人加工时的姿态连续变化),图中显示其右侧已经加工完成。图7b是加工完成的回转体,可以看出,其两次加工后的半回转体间拼合精确,但回转体的最上部回转圆(最后加工的一圈轨迹所在圆),即红线所示的圆与最下部端面不并行,而下部端面平行于机器人基坐标系平面。在CAD模型中上下两个圆平面互相平行,由于加工姿态的变化,导致了加工误差的产生。为了确定上平面加工误差的大小,再次加工一直径为80 mm的半圆柱体,然后测量最后一条加工轨迹与上平面的误差(上平面平行于基坐标系平面),见图7c,图中黑线显示的即为该加工轨迹。测量实际加工圆柱最后一条加工轨迹的最左点与上表面的距离为z1,测量实际加工圆柱最后一条加工轨迹的最右点与上表面的距离为z2,计算两者之间的差值△z,经过多次测量求平均值,得△z= 2.42 mm。
在建立工具镜像模型时,为了验证方法的有效性,采用了双约束的方法,即在图3中,首先在左侧让工具与第二基准长方体的上表面接触并平行,记录机器人末端在左侧的位姿参数。然后旋转机器人末端工具180°,在右侧让工具与第二基准长方体的上表面再次接触并平行,记录机器人末端在右侧的位姿参数。最后将左右侧的机器人末端参数输入到模拟仿真系统中,发现无论如何调整工具模型的位姿,在左右侧,工具模型都无法保证同时与第二基准长方体模型的上表面接触并平行,最好的情况是工具模型在一侧与第二基准长方体模型上表面接触并平行,但工具模型在另一侧只能与第二基准长方体模型上表面平行,无法与其上表面接触,存在一个小的位置误差。发生双约束存在误差以及图7所示变姿态加工误差的原因是机器人本体存在几何参数误差,在标定机器人末端工具时,实际上本体误差也被当成工具安装与制造误差而被部分调整,但由于本体误差与工具误差形成耦合,通过工具标定无法消除本体误差,在某些加工条件下将会形成两者的综合耦合误差。

图7 机器人回转加工回转体实验
3 结语
与机器人末端工具的绝对位姿标定和位置固定的约束标定不同,本文首先建立实际机器人的数字化系统,然后利用数字化系统中的工具模型相对于第二基准模型的约束关系与机器人系统中工具相对第二基准的约束关系一致性,对工具模型的位姿进行调整,实现机器人末端工具的标定。该方法将机器人装备与数字化技术相结合,在提高装备加工精度的同时,有效提高机器人的编程速度,满足数字化制造中的复杂产品定制。
利用装备中的机器人作为测量系统,能够实现现场标定,标定过程简单、方便和标定精度高。但由于机器人本体存在误差,导致标定工具时,其机器人本体误差和工具标定参数耦合,虽然工具标定时部分消除了本体误差,但在机器人装备连续变姿态加工时,形成综合耦合误差。要进一步提高工具的标定精度,首先需要对机器人的本体进行标定,在此基础上再对工具进行标定。后期将利用高精度测量仪器,对机器人的本体进行标定,然后实现机器人本体与机器人末端工具的解耦标定,进一步提高工具的标定精度。
