基于动态压下的楔形板矫直过程仿真模拟研究
2022-08-30陆向辉郭贺松杜兴明陈松亮张君威邵靖斌
陆向辉,郭贺松,杜兴明,陈松亮,张君威, 邵靖斌
(1.河北建材职业技术学院, 河北 秦皇岛 066004; 2.燕山大学 国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004)
0 前言
随着船只、桥梁、建筑等领域的快速发展,楔形板(Longitude Profile Plate, LP板)的重要性越来越高。因其力学性能优异、结构相较于焊接变厚度板更为稳定而受到广泛关注[1-3]。所以高品质的楔形板产品成为了钢铁企业攻关的重点之一。在楔形板矫直的实际生产过程采用改变矫直辊开口度对板带矫直过程进行管控,且完全依靠人工经验的调控手段已经不能满足现场对高品质产品的要求,因此建立一种楔形板矫直过程机理模型指导现场生产很有必要[4]。
矫直是当前板带生产过程保证板带材具有良好几何尺寸与力学性能的关键。针对矫直过程的研究主要以实验、理论解析和数值分析等方法展开,在研究过程中缺乏了对矫直过程机理模型的解释,而且对生产过程的局限性较强,使得楔形板矫直无法实现技术互通。在当前对板带矫直的研究多集中于对常规板带矫直的研究,通过矫直以改善板带材质量[5]。靳皓越[6]为改善板形质量,使用有限元建立了一种基于三维弹塑性有限元法的拉伸弯曲矫直机模型,通过该模型分析张力与插入深度对板形的影响。刘东冶[7]用原始曲率补偿法和塑性变形层增加法对板带变量矫直提供了依据。宋丹龙[8]通过有限元解决了带材拉弯矫直工艺参数对伸长率和平直度的影响进行评估的问题。同时,刘松[9]以连续拉伸弯曲矫直机为研究对象,对厚度、宽度和屈服强度分别在拉弯矫直过程中的能量变化进行了研究。朱剑涛[10]从矫直件的角度揭示了带钢塑性延伸变化规律与矫直过程工艺的关系。邢伟荣[11]从辊系布局角度研究了平行辊矫直对降低板材残余应力的影响。
在楔形板矫直的研究中,祝夫文[12]提出了两阶段楔形板轧制的观点,并建立了楔形轧制的过程控制模型。高娟[13]建立了变厚度板的电液伺服厚度控制系统数学模型,制订了楔形板轧制工艺。国内外关于楔形板矫直理论的研究较少,Cui Li等通过弹塑性差分方法并基于曲率积分研究了LP板矫直过程中变形特征和残余曲率[14]。杜兴明等人[15]针对辊系调整展开研究,提出一种下辊系倾斜的楔形板矫直方式,并获得了良好的矫直效果。
本文研究了楔形板矫直过程轧件截面变厚度矫直辊动态压下与矫直力模型,建立Abaqus有限元仿真模型,分析了楔形板矫直过程压下与矫直力的变化情况,对楔形板矫直工艺优化具有一定的指导价值。
1 楔形板矫直动态压下模型
本文假设普通中厚板的厚度不变,矫直过程中各辊压下量不变,楔形板的厚度是变化的,矫直过程各辊压下量随厚板变化而变化,因此要求矫直设备应具有矫直辊动态调整功能。本研究以某4 300 mm十一辊矫直机作为研究对象,根据实际设备对其进行编号,如图1所示。
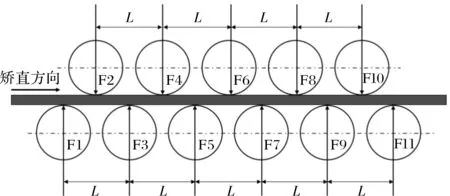
图1 4 300 mm矫直机辊系及编号
1.1 上矫直辊动态压下模型
根据楔形板矫直过程可知:上矫直辊动态压下时会产生压下量使矫直板带产生弹塑性弯曲变形,同时会产生由于楔形板截面厚度变化造成的矫直辊位移,以上两部分叠加构成了楔形板矫直过程动态压下。采用线性递减矫直方式,建立楔形板矫直过程动态数学模型。
设F2压下量为f2(h),F10压下量为f10(h)。则可得上矫直辊的首末机架压下位移为
(1)
(2)
(3)
式中,E为矫直件弹性模量;σt为矫直件屈服强度;L为矫直辊间距;h为矫直板厚;λ为压弯挠度比;ξ为系数,ξ∈[0,1];Cy为相对弹复曲率(弹复曲率与屈服曲率比);Cr为相对残余曲率(残余曲率与屈服曲率比)。
楔形板厚度h为
h=hm+2iΔL
(4)
式中,ΔL为h与hm间的板长,在楔形板表面存在大小为i的坡度。因此可得楔形板矫直过程上辊对矫件的压下量为
(5)
其中,k为各机架编号。
当t=0时,hm处于F1辊正上方,设矫直速度为v,则在t时刻上辊压下量为
(6)
在楔形板实际矫直过程,由于板带厚度不断增加,矫直辊随板带厚度的增加会产生一个向上位移,根据矫直辊运动形态取向下为正方向。则上辊系各辊随板带厚度增加的位移时间函数为
Sk(t)=(k-1)Li-2vti
(7)
可得上矫直辊在楔形板矫直过程的总位移
Tk(t)=fk(t)+Sk(t)
(8)
1.2 下矫直辊压下量模型
在楔形板矫直过程上辊系实现了楔形板矫直过程的线性递减,该部分建立下辊系各辊压下量模型。根据矫直过程辊系分布方式,以上辊系两矫直辊与下辊系的单矫直辊组成一个矫直单元,如图2所示。通过分析矫直过程独立单元计算下辊系各辊压下量。
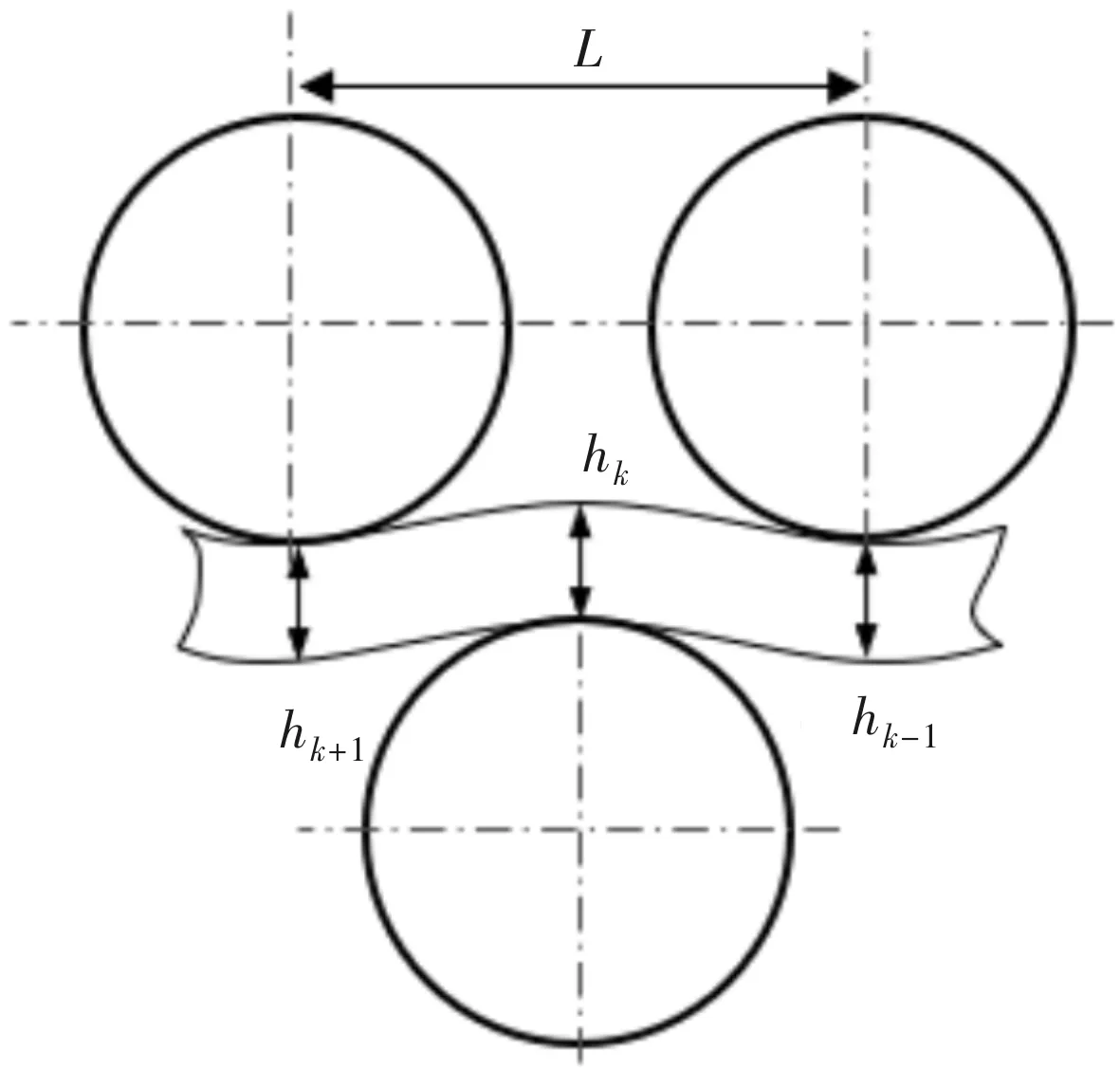
图2 楔形板矫直单元
根据图2可知,在矫直过程各矫直辊对应的矫件厚度变化可以表示为
hk+1-hk=Δh
(9)
Δh=Li
(10)
令k=3,则矫直单元由F2、F3、F4机架组合,此时F2与F4辊的压下量分别为
(11)
(12)
将上辊固定,计算下辊压下量,矫直过程厚度在F3处的理论压下为
(13)
厚度h3处在F2下的压下量为
(14)
厚度h3处在F4下的压下量为
(15)
厚度h3处在F3下理想压下量为
(16)
理论压下量与理想压下量之比为
(17)
由于,h>>Δh,λ>ξ,得
(18)
2 楔形板矫直力模型
当前矫直过程楔形板厚度一般在10~100 mm,i=8。在一个矫直单元内矫直其厚度变化弱,其在矫直过程中与普通板带矫直相同,受到的矫直力与弯曲力矩如图3所示。根据力平衡条件可得矫直辊系各辊的矫直力。

图3 矫直力模型
(19)
(20)
(21)
(22)
依此可得
(23)
3 基于ABAQUS的楔形板矫直过程仿真
本文采用4 300 mm热矫直过程为研究对象,设定建模初始参数,如表1所示。

表1 有限元建模初始参数
创建装备整体的有限元模型,如图4所示。

图4 矫直过程有限元模型
为保证计算精度与计算时间,将该模型划分27 000个单元,其中包括长度方向250单元,宽度18个单元,厚度6个单元。
模拟仿真过程矫直前、中、后状态如图5所示。
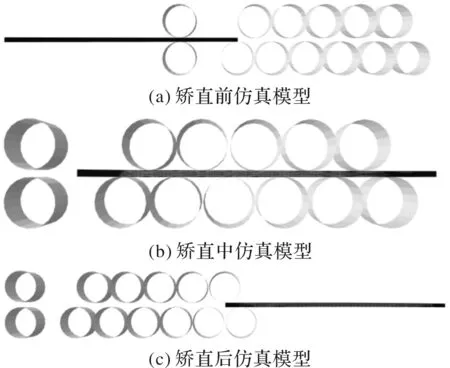
图5 基于有限元矫直模拟
4 计算结果与分析
4.1 有限元模型可靠性验证
为保证有限元仿真数据的可靠性,采集某厂4 300 mm热矫直机生产的规格为SM490A中厚板矫直实测数据。对基于所建模型得到的上辊系各辊矫直力随时间的变化曲线和基于有限元模拟得到的上辊系各辊矫直力随时间的变化曲线进行对比,如图6所示。

图6 可靠性验证
由图6可以看出两种方式得到的矫直力基本相吻合,其误差率保持在10%左右,如图7所示,验证了所建楔形板矫直有限元模型的合理性。

图7 实测数据与仿真数据误差
4.2 楔形板矫直过程压下量分析
根据以上建模过程对楔形板矫直过程压下量进行分析,如图8所示。当楔形板矫直过程中,随着楔形板截面厚度增加,上辊系各矫直辊压下逐渐降低。但是随楔形板截面厚度变化,上辊系末两机架压下变化不明显。

图8 上辊系压下量随板带截面改变的规律
由图9可知,随矫直进程,各矫直辊的总位移都向上,零线以上的值为初始压下量,线上各点纵坐标改变值为由于楔形板截面厚度增加产生的压下量改变值和上辊位移值之和。
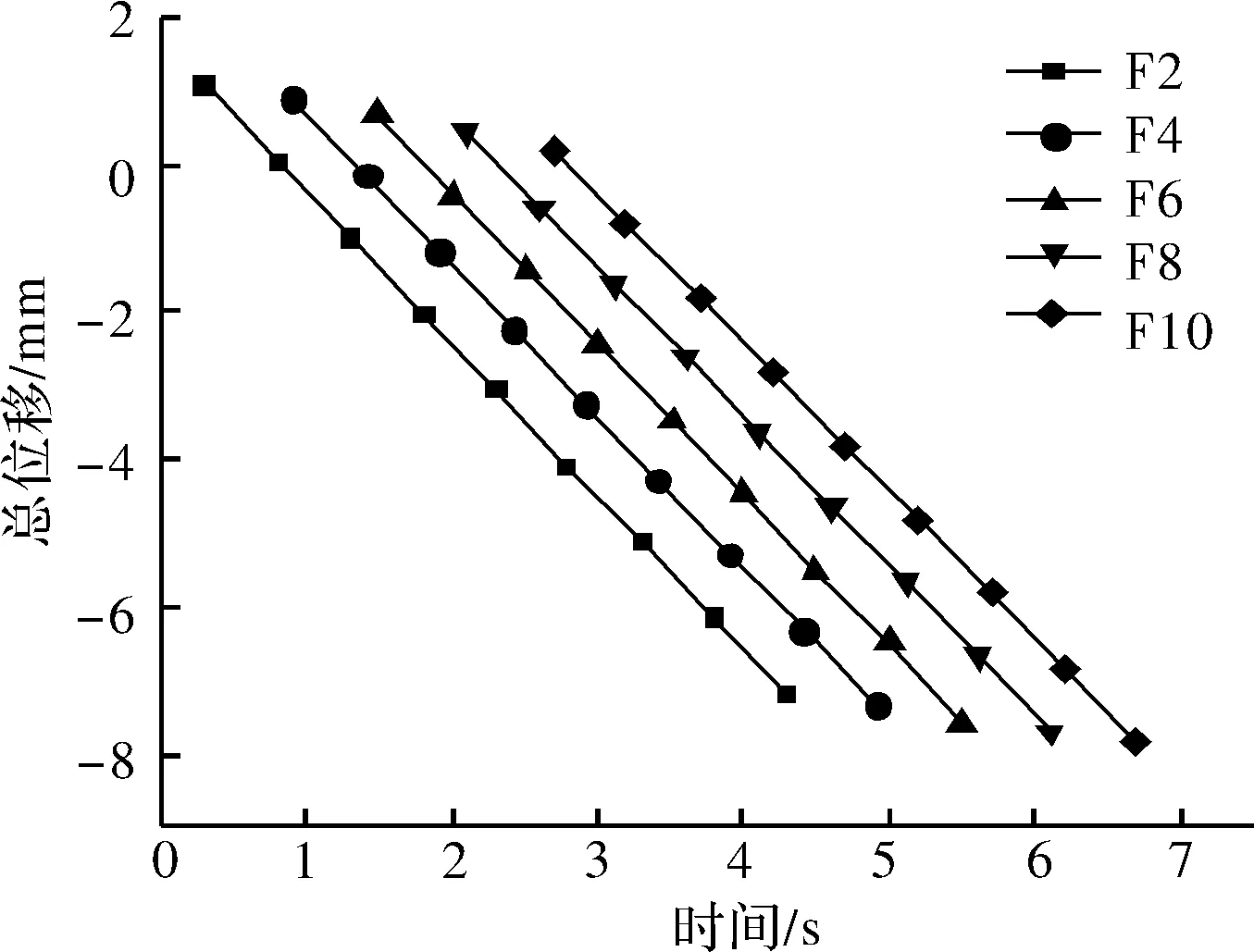
图9 上辊系各辊位移随时间变化
由图10可知,理论压下量和理想压下量误差较小,表明用线性递减矫直方式矫直该楔形板时,压下量符合线性递减规律。
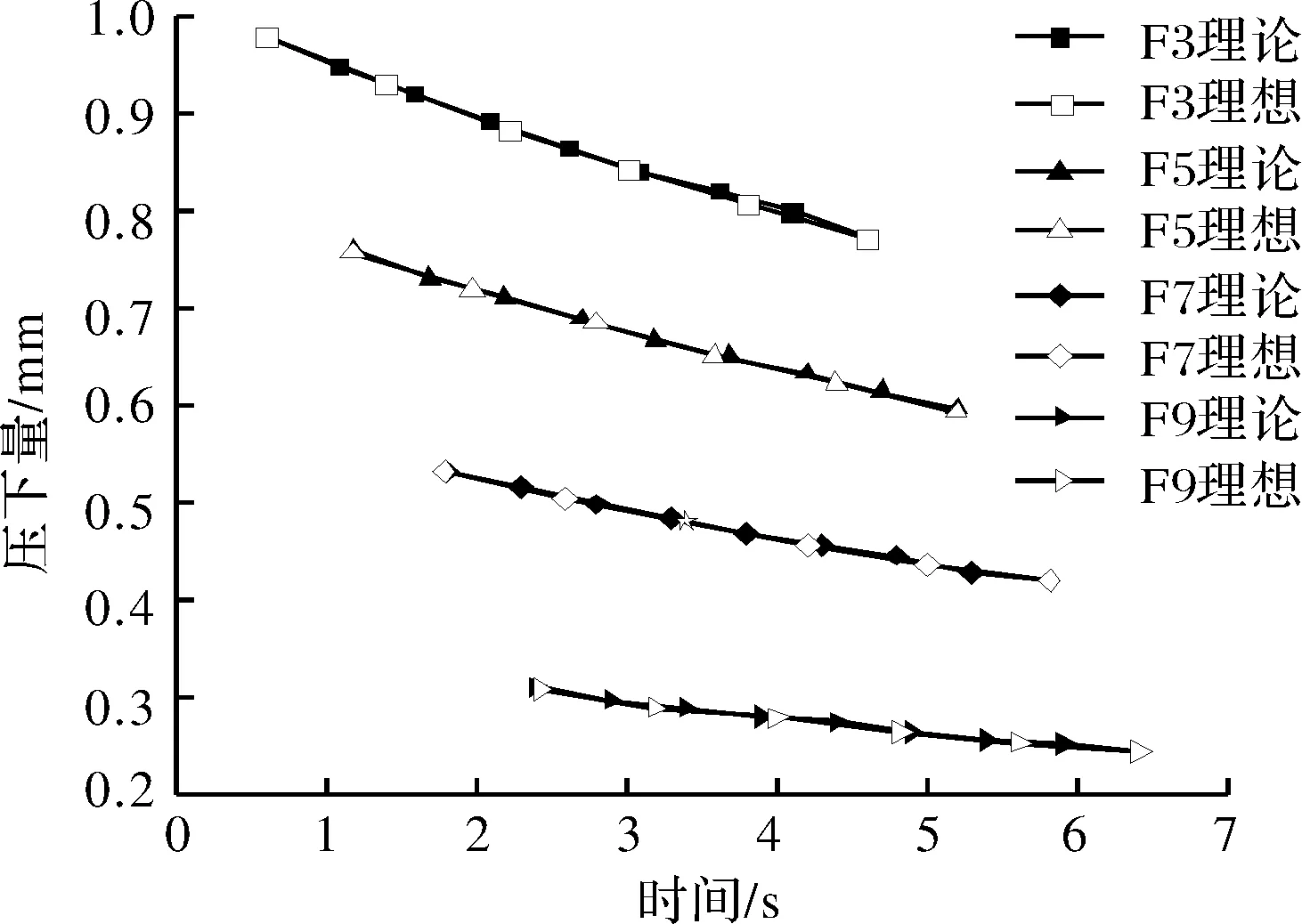
图10 下辊系理论与理想压下量对比
4.3 楔形板矫直力分析
在矫直过程假设整个过程处于稳定状态,得到各辊矫直力,如图11所示。在理论建模过程,省去了咬入阶段的不稳定性,可知在矫直过程,楔形板厚度不断增加致使各矫直辊矫直力增大。可以看出,矫直力在F4处最大,其原因是由于在前机架相对反弯曲率较大,矫件经过前机架现对残余曲率也较大,因此造成F4处矫件总相对弯曲率较大,造成该处矫直力最大。

图11 本文建立模型的上辊系矫直力
在有限元模型中,可以看出在稳定矫直阶段其轧制力与建立的理论模型矫直力基本一致,证明了模型的有效性,如图12所示。
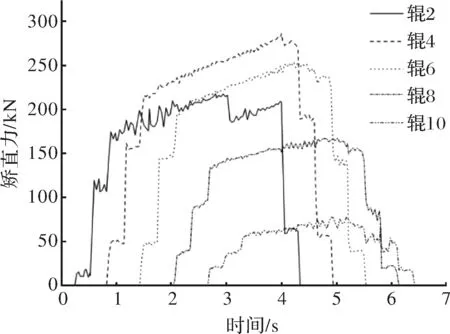
图12 基于有限元仿真的矫直力曲线
5 结论
本文通过对楔形板矫直过程压下量及矫直力模型的计算,解决因楔形板变截面厚度矫直过程中的动态变化问题,并采用Abaqus有限元进行仿真模拟,主要结论如下。
(1)用线性递减方案矫直楔形板时,理论压下量与理想压下量之比接近1,满足递减规律压下要求。
(2)通过有限元仿真分析,验证了理论模型与仿真模型的一致性,为后续优化矫直工艺提供了研究基础。
(3)对楔形板矫直过程,矫件的楔度越大,造成后续矫直压力越大,矫直难度也会增大。
