基于AHP-RS的重型装备网络化协同制造任务粒度评价体系研究

赵紫京郧，苏振华，王富强，刘 颖，余京宴，闫子威

(1.重庆大学机械与运载工程学院，重庆400044；2.中国重型机械研究院股份公司，陕西 西安710018；3. 国机重型装备集团股份有限公司，四川 德阳 618000)

0 前言

复杂重型装备通常为高端装备，是国家高端制造能力和水平的体现，也是国防工业和基础建设的重要保障，广泛应用于工程机械、航空航天、能源、交通、船舶、冶金、军工等重点行业和领域，是国家重点发展的战略性产业之一。不同于其他普通装备，复杂重型装备具有研制周期长、制造体量大、技术含量高、设计领域广泛等特点[1]。故其制造模式多为：一个项目总包企业(大型装备制造企业或科研院所等)和多个协作企业联合，总包企业在掌握核心技术的前提下，借助社会优质资源进行制造，即网络化协同制造模式。对于此类制造模式而言，各级任务的合理分解是开展工作前的必备环节，任务分解结果的有效性也决定了后续项目的顺利开展。其中，任务粒度作为任务分解后各子任务的重要属性之一，是任务分解结果的一种直观表现，因此，从任务粒度的角度对任务分解结果进行评价对于复杂重型装备网络化协同制造模式的顺利进行意义重大。

目前，在网络化协同制造模式下，任务粒度已有了较为广泛的应用。对任务粒度概念本身，庞辉[2]等对其进行定义，他认为任务粒度代表了产品在设计与加工过程中所涉及的活动聚合程度，既可以表现为任务的组织形式，又可以反映任务的规模和数量。曹勤伟[3]等在此基础上进一步拓展，认为任务粒度可以用任务粒度系数和任务数量的关系来表示，以衡量团队内部子任务的聚合程度。

在考虑任务粒度的影响因素方面，Xu[4]等将任务粒度本身作为考虑因素，基于系统工程原理，提出了一种任务分解方法，通过设定任务粒度阈值以判断当前任务分解方案是否合适。Liu[5]等同样从任务粒度本身特征出发，针对复杂产品集成制造系统中的任务分解与任务调度之间的协同问题，提出了一种任务粒度定量分析方法，以指导粗粒度任务分解和低内聚系数子任务重组。

在任务粒度的评价方面，包北方[6]等对任务分解后任务粒度本身、任务耦合度以及任务均衡度分别进行了分析和判定，并以此建立了任务分解系统模型。王龙[7]从制造资源服务的角度出发，对任务的执行时间、服务成本以及质量指标等因素进行了评价，建立了云制造环境下的制造资源服务组合指标体系。冀翔[8]针对众创设计中的设计任务粒度展开研究，指出设计任务粒度主要由设计需求、设计过程和设计结果等方面综合而成，并对其从关联度、影响度以及灵敏度三个方面进行了评价。高斐[9]提出了一种动态多角色的管理任务层级分解算法，算法兼顾了分解后子任务的负载平衡性和饱和度，并分别进行了指标评价。

上述研究成果从任务粒度的定义、影响因素出发，对网络化协同制造模式下任务分解后的任务粒度就不同方面进行了评价指标的研究，但均仅针对个别指标展开，未形成系统化的任务粒度评价指标体系，且缺少一套合适的指标评价方法。为此，本文以复杂重型装备网络化协同制造模式为研究对象，对其任务分解后的任务粒度评价方式展开研究，在上述研究成果的基础上，建立一套系统化的任务粒度评价指标体系，并给出相应的评价方法，最后进行实例分析，以验证本文指标体系和评价方法的可行性。

1 问题描述

目前，随着客户对于产品定制化程度要求的进一步提高，不同企业之间、企业同供应商之间，乃至企业同客户之间的协作范围以及协作程度正在逐步加深，越来越多的企业、供应商以及客户参与到了以核心企业为主体的产品网络化协同制造模式当中。这种制造模式往往依托于网络化协同制造平台，利用各类产品定制协同工具、信息集成与冲突消解技术、共享服务器、定制系统知识库等，对客户需求进行分析映射，对产品定制部件设计任务进行科学分解与合理分配，最终共同完成定制产品的设计[10-12]。

本文以项目总包为设计单位的复杂重型装备网络化协同制造模式为对象展开研究。其基本模式流程如图1所示。

图1 复杂重型装备网络化协同制造模式

在复杂重型装备网络化协同制造模式下任务分解流程大致分为三步，分别为顶层任务分解、二级任务分解以及任务聚类。为了保证后续任务-资源匹配流程的顺利进行，在任务聚类完成之后，需要对聚类结果进行评价。其中，对于任务粒度的评价尤为重要，该步骤须确保任务分解完成后得到的各子任务粒度本身大小合适、各属性符合要求，从而保证当前任务粒度在目前网络化协同制造平台的资源水平支持区间之内。因此，建立合适的任务粒度评价体系对于复杂重型装备网络化协同制造模式的顺利进行具有重要意义。

任务粒度的评价过程受到多维度、多方面的因素影响。从不同的评价维度来看，任务粒度评价可以分为子任务个体和项目总体两个维度，同时，两个维度又相对应地涉及不同方面的因素，如任务内聚性、任务耦合性、项目协同性等。显然，不同因素的影响机制及影响程度也有所不同，故合理的任务粒度评价体系应当充分考虑上述各维度、各方面的因素，以此确保任务粒度设计的合理性。基于此，本文拟在探讨如何保证任务粒度评价结果合理性的前提下，从上述两个维度进行分析，结合各维度下不同影响因素进行考虑，明确各因素评价的指标，并对各指标赋予合适的评价权重，以此构建任务粒度评价体系，为复杂重型装备网络化协同制造模式下任务分解流程中的任务粒度评价环节提供参考。

2 复杂重型装备网络化协同制造任务粒度评价指标体系构建

本文在参考有关文献及资料的基础上，结合复杂重型装备网络化协同制造特点，基于系统性、合理性、关键性的构建原则，按绝对性、相对性进行划分，从子任务和项目两个维度出发，建立任务粒度评价指标体系，用于评价该模式下任务分解后各子任务粒度的合理性，具体的指标体系如图2所示。

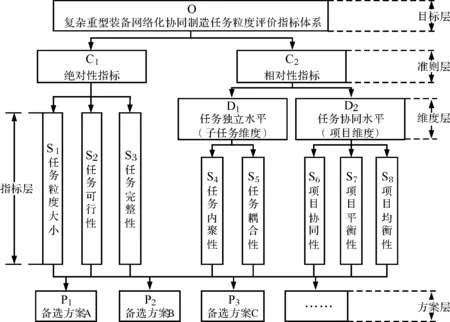
图2 复杂重型装备网络化协同制造任务粒度评价指标体系

指标体系有5个层级。第一层为目标层，即本文的主要研究内容——任务粒度评价指标体系本身。第二层为准则层，这里按照指标性质将指标划分为两类，分别绝对性指标和相对性指标。绝对性指标指在进行任务粒度评价时，某一指标为硬性要求即需要绝对满足；相对性指标则指在评价时仅进行不同方案间比较，本身并无硬性要求的指标。在进行任务粒度评价时，对于绝对性指标，需要事先根据平台实际情况设定指标阈值，并优先进行判定，指标大小须保证在阈值范围内，否则当前任务分解方案无效，需重新制定。对于相对性指标，是在绝对性指标全部满足后再进行评定打分，基于不同指标影响程度的差异，对指标赋予影响权重，从而加权判定可行方案中得分最高的最优方案。第三层为维度层，主要对相对性指标进行分类，分为任务独立水平指标和任务协同水平指标，分别反映了上文所划分的子任务维度和项目维度。第四层为指标层，本文共提出8项任务粒度评价指标，在进行任务粒度评价时即遵循各项指标的定义分别进行。第五层为方案层，为各备选方案，任务粒度评价即对不同备选方案分别进行。

指标层中有8个指标。

(1)任务粒度大小。顾名思义，任务粒度大小即为任务粒度本身的直接量化表示，这里选用任务粒度值来进行计算。任务粒度值计算如下式所示[6]：

(1)

式中，对于当前任务集T而言，GT即为其任务粒度值，k表示任务粒度系数，取值同任务之间的关联程度相关，本文取任务内聚系数作为任务粒度系数，关于任务内聚系数的详细描述将在后文进行说明，n表示项目集T中所含有的子任务数量，且有GT>0,k>0,n>0。任务粒度值从项目整体的角度反映了任务粒度水平，同任务数量及任务间联系直接相关。

在评价体系中，任务粒度大小为绝对性指标，在进行任务粒度评价时，需根据实际情况设立阈值，任务分解后任务粒度值计算结果不能超出阈值，否则认为任务分解无效。

(2)任务可行性。任务可行性要求任务分解后得到的任务集可以被完成，这里用任务负载水平进行评定。任务负载水平的计算如下式所示：

(2)

式中，Lt表示当前子任务t的负载水平，li指该子任务中元任务Mi的相对复杂度系数，m表示子任务中t的元任务数量。其中，li的值基于平台现有资源水平确定，若li小于1，说明该元任务的相对复杂度较小，在当前资源水平的支持范围之内，可以完成且有一定的资源富余；若li大于1，说明该子任务的相对复杂度较大，超出了当前的资源水平支持范围，无法直接完成，需要占用其他元任务资源。显然，Lt反映了当前子任务中各元任务t的平均任务负载水平，若Lt小于1，则表明分解后该子任务的负载水平合适，能够满足现有资源水平支持，若大于1，则表明该子任务的平均负载水平过高，当前资源水平无法支持，需要继续分解。

在评价体系中，任务可行性为绝对性指标，在进行任务粒度评价时，需保证各子任务负载水平均小于1，否则认为任务分解无效。

(3)任务完整性。同任务可行性类似，任务完整性也反映了任务分解的有效性。任务分解过程为将某一层级任务分解为若干个子任务，并组成相应的任务分解集合，在这一过程中，需要保证当前层级任务分解后的子任务完整，即不存在任务的缺失和重复。任务完整性没有直接量化的评定指标，但可用公式表示为

(3)

式中，tj为任务分解后的各子任务，T为任务分解集，即分解后应保证由子任务组成的集合能够同项目组成保持一致。

在评价体系中，任务完整性为绝对性指标，在进行任务粒度评价时，需保证任务分解结果能够满足上式，否则认为任务分解无效。

(4)任务内聚性。任务内聚性指任务分解完成后各子任务内的聚合程度，选用任务内聚系数进行计算。

(4)

式中，任务内聚系数C(T)通过任务关联内聚系数c(t)和任务重用内聚系数r(t)的乘积求和取平均进行表示。在给出任务关联内聚系数和重用内聚系数的定义之前，首先需对活动约束结构的概念加以说明。

所谓活动约束结构即指一个活动的基本组成部分，可以用一个二元组(D,O)来表示。其中，D表示该活动约束结构中的有限个活动单元；O={(p,cs)∈D×P(D)}是由一系列约束控制元所组成的约束控制集；p表示输出活动单元；cs表示由若干个输入活动单元组成的集合，(p,cs)即为一个由活动单元构成的约束控制空间下的约束控制元，属于由活动单元构成的约束结构空间。一个子任务t则是对于给定的活动约束结构(D,O)中的任意一个约束控制子集，即有t∈O。一个约束控制元由一组输入和输出的活动关系构成，参考文献[2]中的表示方法，定义本文的基本约束控制结构共有两种类型，如图3所示。

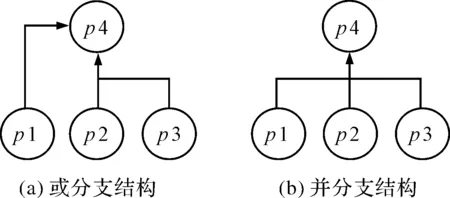
图3 基本约束控制结构

网络化协同制造过程中的每一个任务都是基于图中的两种活动约束结构，按照既定的工作流程进行。由于活动之间存在关联性，对于两个不同的任务，某一任务输出的活动有可能便是另一任务的输入，除此之外，同一任务中的不同活动之间可能也会存在这种关联现象。由此，便可引出任务关联内聚系数的计算公式。对于一个基于活动约束结构(D,O)的有效约束子集，即子任务t，其任务关联内聚系数c(t)为

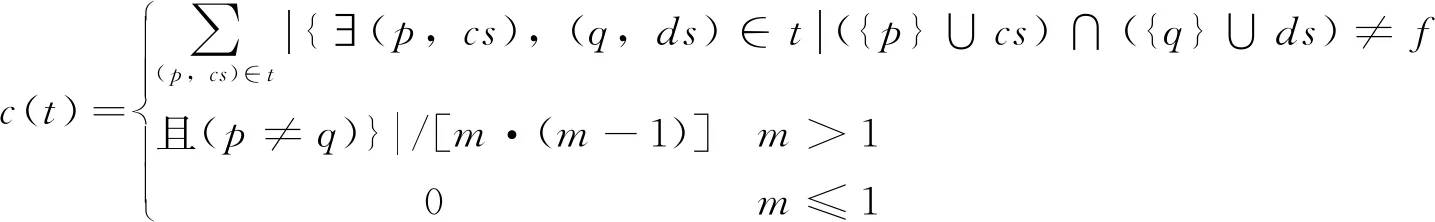
(5)

式中，m表示子任务t中约束控制元的数量，(p,cs)，(q,ds)表示在子任务t中的任意两个输出活动单元不同的约束控制元，公式表示在一个子任务t中，任意两个输出活动不同的约束控制元中相同活动单元出现的次数和该子任务t中约束控制元排列集数量m·(m-1)的比值。对于一个给定的子任务t而言，其控制元排列集数量为定值，因此c(t)越大，则说明某一约束控制元中的输入或输出活动在其他约束控制元中出现的次数越多，不同约束控制元之间的信息交互也就越多。即任务关联内聚系数反映了在当前任务粒度下，该任务中不同约束控制元之间的关联水平。

在上述理论的基础上，同时可引出任务重用内聚系数的概念。对于一个基于活动约束结构(D,O)的有效约束子集，即子任务t，其任务重用内聚系数r(t)为

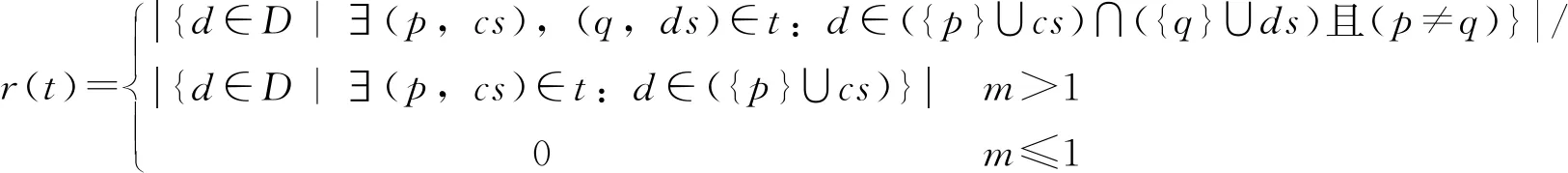
(6)

式中，d表示子任务中的活动单元，公式表示在一个子任务t中，任意两个输出活动不同的约束控制元中相同活动单元的数量和该子任务中所有活动单元数量的比值。对于一个给定的子任务t而言，其包含的所有活动单元数量为定值，因此r(t)越大，说明该子任务中重用的活动单元数量越多。即任务重用内聚系数反映了当前任务粒度下，该任务中活动单元的重复水平。

综上，任务内聚系数反映了任务分解后各任务总体的内聚程度，越大说明分解后项目整体内聚性越好。

在评价体系中，任务内聚性为反映任务独立水平的相对性指标，在进行任务粒度评价时，需同其他相对性指标进行加权综合比较，以此确定备选方案的优劣性。除此之外，由于任务粒度系数表达了任务之间的关联性，故这里也将任务内聚系数作为任务粒度值计算过程中的任务粒度系数。

⑤任务耦合性。任务耦合性指任务分解完成后各子任务之间的耦合程度，选用任务耦合系数进行计算。

(7)

式中，cond(s,t)表示在同一项目中，任意两个子任务的耦合关联指数。为方便表述，引入耦合信息关联矩阵的概念。耦合信息关联矩阵为一个n×n的方阵，n表示项目中子任务的数量，矩阵的行、列分别对应相同的子任务，矩阵内各元素即cond(s,t)，代表矩阵行任务同矩阵列任务之间是否存在信息交互。若任意两个子任务s,t(s≠t)中存在相同的活动单元，则认为两个任务之间存在信息交互，此时，cond(s,t)为1，否则为0；同一子任务的耦合关联指数为0，即cond(s,s)=0。矩阵所有元素的和，即∑cond(s,t)为项目中子任务间信息交互的次数，由此即可求得项目的耦合系数U(T)。项目耦合系数反映了项目经任务分解后不同子任务之间的交互程度，U(T)较大说明分解后不同子任务之间的交互较多。

在评价体系中，任务耦合性为反映任务独立水平的相对性指标，需要同其他相对性指标进行加权综合比较，以此确定备选方案的优劣性。

(6)项目协同性。基于上述对于任务内聚性和耦合性的讨论，这里更进一步给出项目协同性的概念。项目协同性反映了任务分解完成后任务集整体的联系性，这里的联系性特指任务耦合性和任务内聚性的相对水平。为了使后续进行任务-资源匹配流程时各任务能够准确匹配到对应资源，需要保证任务分解后的任务集内各子任务本身具有较强内聚性，同时子任务之间具有较弱耦合性，即需要满足高内聚、弱耦合的原则，反映在具体的指标上即要求任务内聚系数越大，同时任务耦合系数越小越好。故此处为了综合评定任务的内聚性和耦合性，引入项目耦合/内聚系数比率λT进行计算，如式(8)所示。

(8)

显然，若λT越小，则说明此时项目中子任务间耦合程度小，任务内聚程度大，既有利于项目资源在任务间的分配，同时也有利于单个任务的实施乃至整个项目的进行，即项目协同性较好。

在评价体系中，项目协同性为反映任务协同水平的相对性指标，在进行任务粒度评价时，需同其他相对性指标进行加权综合比较，以此确定备选方案的优劣性。

(7)项目平衡性。项目平衡性指任务分解后项目整体的负载情况，任务分解完成后，为使得后续任务执行过程的各环节不会出现严重的延滞，需保证项目整体的负载平衡性，这里选用项目负载平衡系数和项目负载平均饱和度进行计算[9]，以下对其分别进行说明。

在计算项目负载平衡系数前，首先需要对项目及项目中各子任务的负载水平进行计算。其中，针对各子任务的负载水平在上文中已有过论述，此处对项目负载水平进行讨论。对于一个基于活动约束结构(D,O)，且由若干子任务组成的项目T，其项目平均负载水平定义为

(9)

基于上式，进而对项目负载平衡系数进行计算，对于项目T而言，其项目负载平衡系数表示为

(10)

这里以各子任务负载水平方差的形式作为项目负载平衡系数LBT，LBT反映了当前任务分解结果下项目负载的平衡性水平，显然，LBT越小，则表示当前任务分解结果对应的项目负载平衡性越好。若LBT=0，则认为此时任务分解结果对应的项目达到了负载绝对平衡。

同样地，对于一个基于活动约束结构(D,O)，且由若干子任务组成的项目T，其项目负载平均饱和度定义为

(11)

式中，ηT为项目T的负载平均饱和度，LR为平台的资源水平，本文中默认为1。ηT反映了项目T所对应的负载饱和状态，由上式可知，ηT∈[0,1]，ηT越接近0，说明此时LT越接近LR，即项目负载更趋于饱和状态，资源利用率较高，此时项目任务分解效果较好；ηT越接近1，说明此时LT越接近0，即项目负载更趋于空载状态，存在资源的浪费，此时项目任务分解效果较差。

在评价体系中，项目平衡性为反映任务协同水平的相对性指标，在进行任务粒度评价时，需同其他相对性指标进行加权综合比较，以此确定备选方案的优劣性。

(8)项目均衡性。项目均衡性是项目整体在大小、规模上均匀程度的量化水平。在复杂重型装备网络化协同制造模式下，由于其产品工艺复杂、涉及工艺种类多样，其任务之间往往存在较强的关联性，单一任务的延滞即有可能影响整体项目的进行。故使得不同任务尽可能处于同一水平，从而令项目整体具有较好的任务均衡度对于复杂重型装备项目的顺利执行具有重要意义。

本文选取任务执行时间均衡度作为项目均衡性的综合考量指标。对于一个基于活动约束结构(D,O)，且由若干子任务组成的项目T，其任务执行时间均衡度定义为

(12)

在计算E之前，首先需要确定项目中各子任务的执行时间，考虑到任务分解过程结束后，各子任务实质上为不同元任务的集合，故其任务执行时间可由所组成的各元任务决定。若各元任务为独立、依赖及串并行关系，其执行时间即为单纯的各元任务执行时间累加，即

(13)

若各元任务为耦合重叠型关系，则其组合得到的子任务执行时间计算相对复杂，这里参考文献[6]，采用高斯消去算法来进行计算。假设某子任务中元任务M1和M2具有耦合关系，且其执行时间分别为|tM1|和|tM2|，则子任务的执行时间表示为

(14)

式中，dM1,dM2分别表示元任务M1对元任务M2、元任务M2对元任务M1的交互耦合系数。若两个元任务之间的耦合性越强，则相应地由其组成的子任务所对应的执行时间也会更长。

在评价体系中，项目均衡性为反映任务协同水平的相对性指标，在进行任务粒度评价时，需同其他相对性指标进行加权综合比较，以此确定备选方案的优劣性。

3 基于AHP-RS的相对性评价指标组合权重计算

对于任务粒度评价体系中的相对性指标，需要对其进行相对重要性判定从而确定指标权重，以此来评价可选任务粒度方案的优劣性。

考虑到复杂重型装备产品工艺复杂，各环节的评定过程除通过具体的指标进行量化的直接评价之外，往往还需要人为进行核对，受到一定的主观性影响。故在进行相对性评价指标权重确定的过程中，需要同时考虑主观和客观权重，本文提出一种基于AHP-RS的权重确定方法。

3.1 基于AHP的指标主观权重确定

层次分析法(AHP)是由美国匹兹堡大学教授T.L.Saaty在20世纪70年代中期提出的。其思想是把复杂的问题分为若干因素，并将因素按对应关系分组，形成一个有序的递阶层次结构。通过两两比较的方式确定层次中诸因素的相对重要性，并综合人的判断以确定相对重要性的总排序[13]。其基本流程如下：

(1)建立递阶层次结构。明确分析系统中不同层级之间以及同一层级内部各因素之间的关系，并由此建立对应的递阶层次结构，本文的层次结构即如上文建立的任务粒度评价体系所示。

(2)构建判断矩阵。对同一层次上的指标进行两两比较确定其相对重要性，并由此构建判断矩阵。其中，本文因素相对重要性评定的标准按照9级标度表确定。

(3)一致性检验。为保证各因素之间的相对重要性评判未出现明显偏差，需要对矩阵进行一致性检验，通过计算矩阵特征值λmax，并以此计算一致性指标比率CR，需保证CR<0.1，才认为判断矩阵有效。CR计算公式为

(15)

式中，n为判断矩阵的阶数，RI为随机一致性指标，其取值由判断矩阵阶数决定。

(4)主观权重计算。一致性检验通过后，即可基于指标间的相对重要性，对各因素的主观权重进行计算。

基于收集到的相关资料以及行业专家的意见，对任务粒度评价体系中的相对性指标两两进行相对重要性评定，以此建立判断矩阵，并进行一致性检验，得到各评价层下的判断矩阵及检验结果如表1所示。

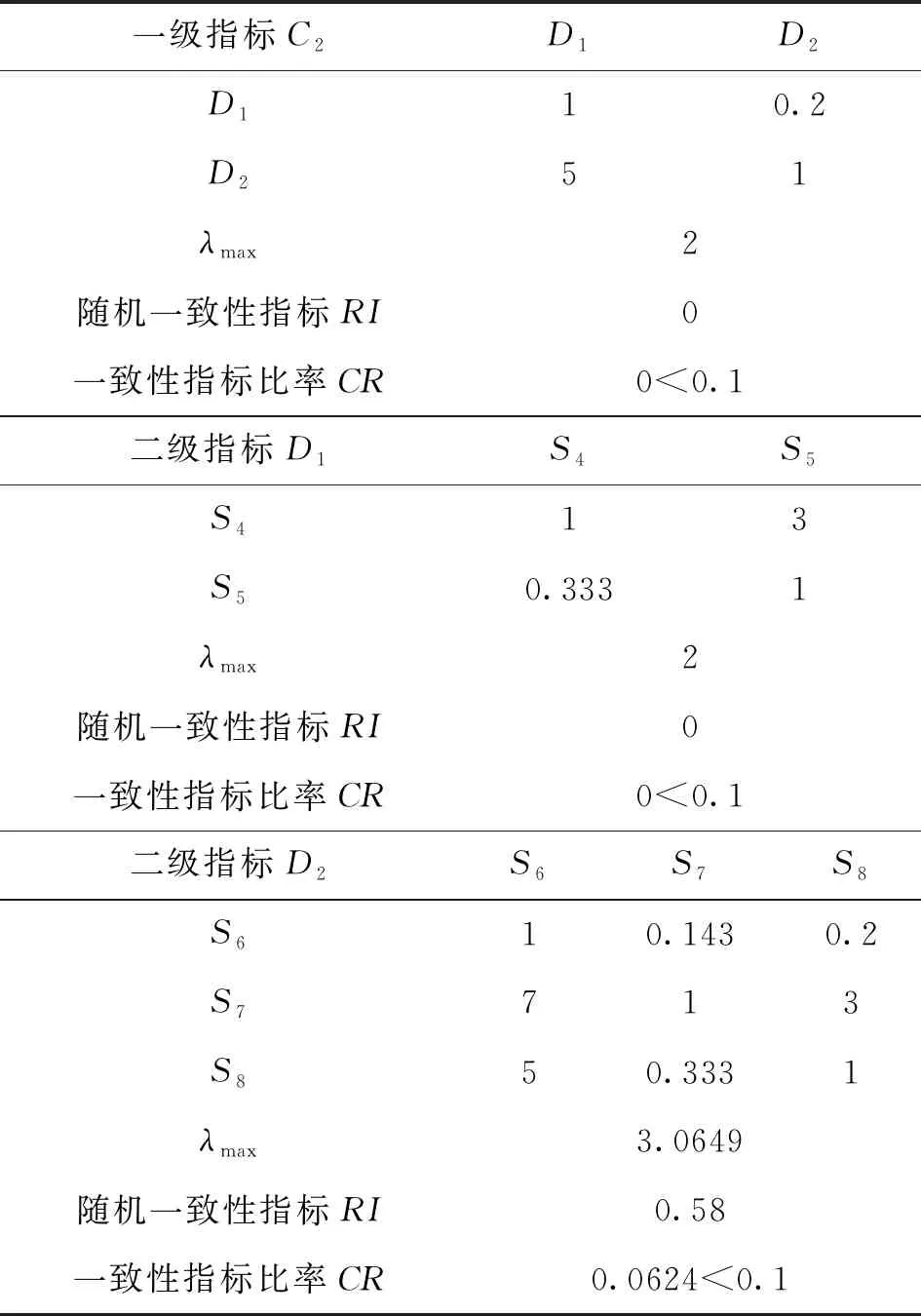
表1 各层级判断矩阵及一致性检验结果

如表1结果所示，各层级判断矩阵均通过一致性检验，即相对重要性评定有效。对上述结果进行整理，计算不同层级下各相对性指标的综合权重，结果如表2所示。

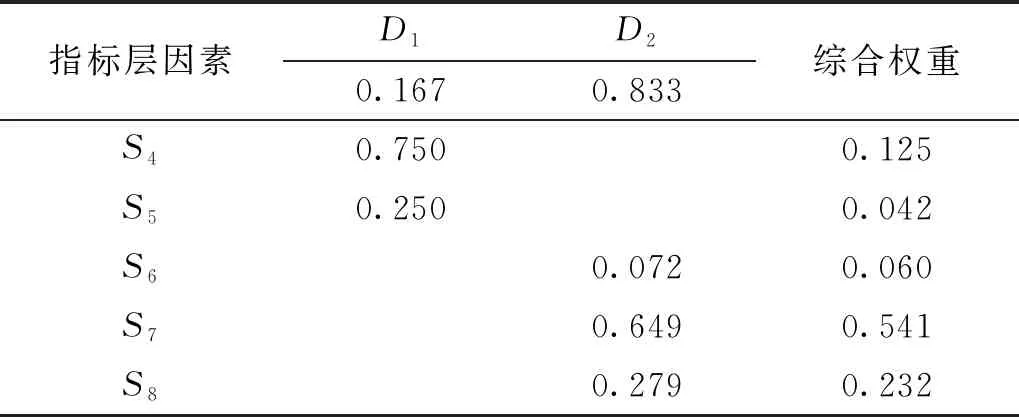
表2 相对性指标主观权重

3.2 基于粗糙集法的指标客观权重确定

粗糙集(RS)是指在信息系统分类能力保持不变的条件下，对信息系统进行属性约简，得到信息系统分类规则的一种方法[14,15]。本文对该方法涉及的3个概念进行了定义。

定义2 信息量。在一个信息系统中，若P⊆A有，则由P确定的二元不可区分关系可以表示为：ind(P)，且有ind(P)={(x,y)∈U×U|∀a∈A,f(x,a)=f(y,a)}，U/ind(P)={X1,X2,…,Xn}，则P的信息量可定义为

(16)

式中，|U|、|Xi|分别表示整个论域当中的对象个数以及Xi中的对象个数。

定义3 属性重要性。对于∀a∈A,ai属性的重要性定义为在A中去掉属性ai后引起的信息量变化程度，用sigA-{ai}表示，即有

sigA-{ai}=I(A)-I(A-{a})

(17)

通过计算得到各属性对应的sigA-{ai}，进而进行加权，即可得到各属性所对应的权重，用ωai表示，即有

(18)

根据上述定义给出基于粗糙集法的指标客观权重确定步骤如下：

(1)构建信息系统。基于任务粒度评价体系以及样本数据构建对应的信息系统。其中，评价体系中的各相对性指标即为信息系统的属性，各样本点为对象，样本数据为属性值。

(2)信息系统属性的重要性度量。根据式(16～17)，对任务粒度评价体系中的各相对性指标的信息量以及信息量变化程度进行计算。

(3)指标权重确定。根据式(18)，对各指标的客观权重进行计算。

按照上述步骤，本文选取10个复杂重型装备历史项目作为样本进行测评，决策属性值取V={1,2,3,4,5}共5个等级，等级越高表示任务分解后得到的任务粒度越合适，对应指标的效果越好，由此得到的样本评价结果如表3所示。

表3 样本相对性指标评价结果

由此计算得到各层级相对性指标客观权重，结果如表4所示。

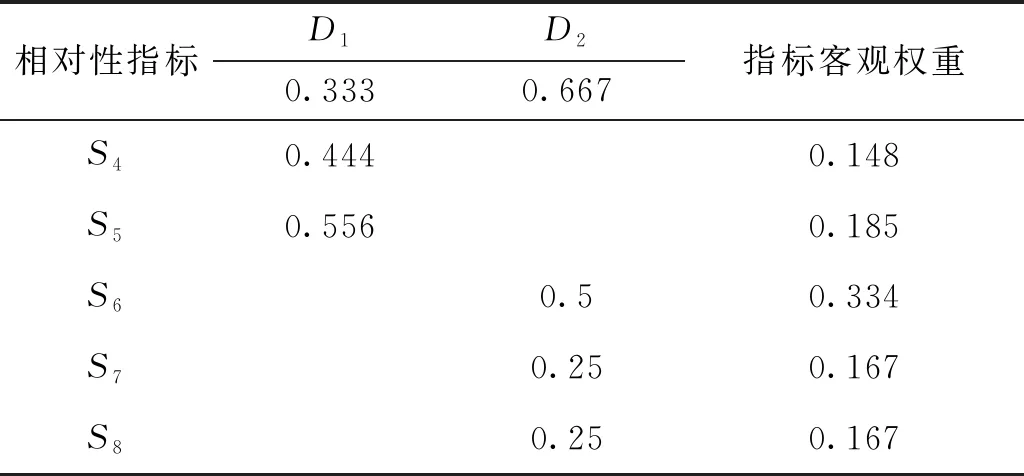
表4 相对性指标客观权重

3.3 基于组合权重的评价模型

所谓组合权重即将基于AHP法得到的指标主观权重同基于粗糙集法的指标客观权重进行结合，保证最后的任务粒度加结果同系统真实状态的误差最小，以此达到最优的评价效果。设指标主观权重为ωs，指标客观权重为ωo，组合权重为ωc，引入参数μ，以此建立优化模型[13]，即

(19)

可以证明，上述模型在可行域Ωc上有唯一解，其解为

ωci=μωsi+(1-μ)ωoi,i=1,2,…,n

(20)

证明如下：

作Lagrange函数

(21)

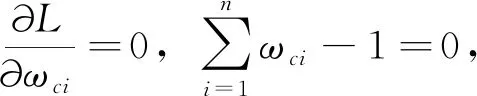
(22)

解上述方程组即可得证。

其中μ可视作指标主观权重ωs同客观权重ωo的影响因子，反映了两者对于组合权重的影响程度。本文根据有关材料，取黄金分割数，即μ=0.382进行计算，由此得到相对性指标组合权重如表5所示。

表5 相对性指标组合权重

基于上述指标组合权重最优值的计算，即可建立对任务粒度相对性评价指标的评价值数学模型。设Wcj、ωci(i=1,2,…,n;j=1,2,…,m)分别为评价模型中维度层和指标层中各指标的组合权重，vi为研究对象O在该指标下的评价值，则O任务粒度评价的得分可以表示为：

(23)

其中，m,n分别表示评价体系中维度层和指标层中的指标个数。

根据任务粒度评价得分结果，对任务粒度的设计合理性进行评级，共分为5个等级，各等级同评分的对应关系同表6所示。

表6 任务粒度合理性评价等级

4 案例分析

以国内某重型装备研究院Z企业125 MN挤压机主工作缸定制研发设计项目为研究对象，用本文提出的基于AHP-RS的复杂重型装备网络化协同制造任务粒度评价体系对其任务分解后的任务粒度方案进行评价。

该挤压机主要用于生产大型铝型材、铝棒材、铝管材等，在我国国防工业和基础建设中发挥着重要作用，是典型的复杂重型装备，在其设计过程中有着高度定制化的需求，125 MN挤压机的结构如图4所示。

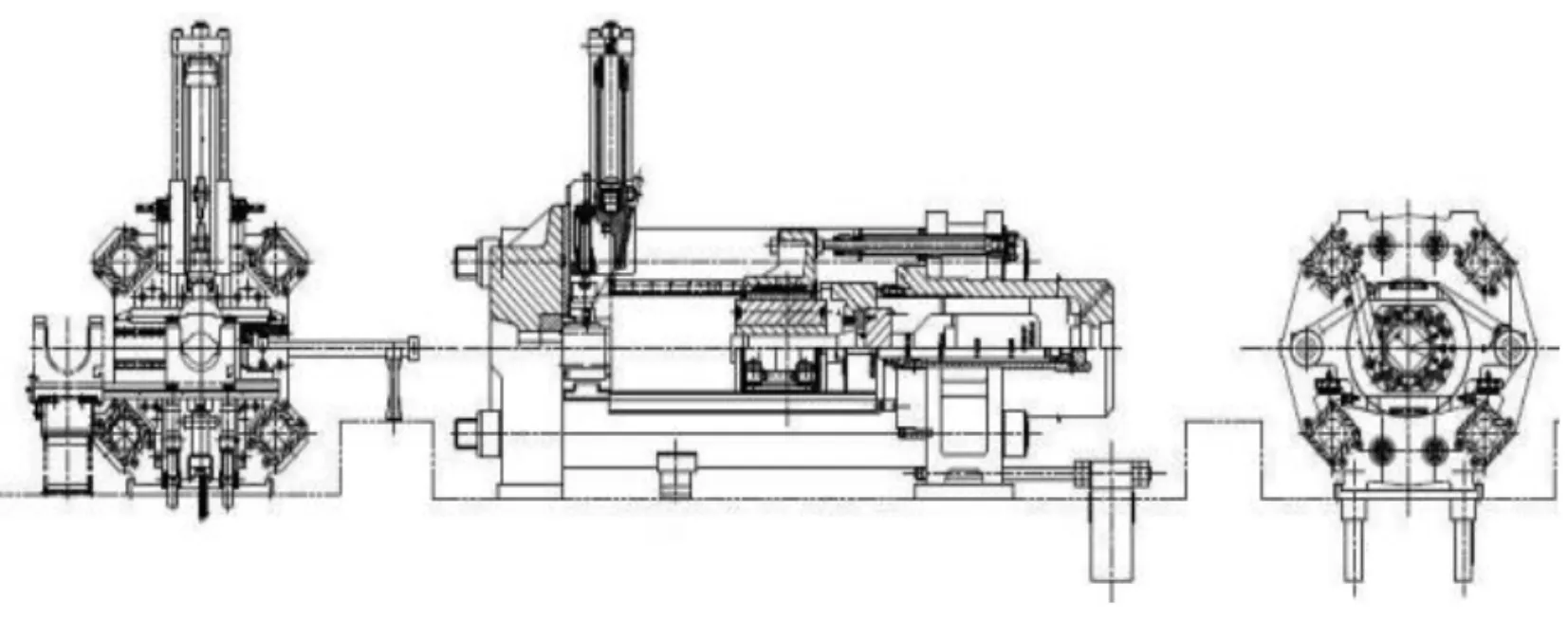
图4 125MN挤压机结构图

其中，主缸项目研发设计活动的实施流程如图5所示。

图5 125 MN挤压机主工作缸定制研发设计项目活动实施流程

该流程按照125 MN挤压机主工作缸的结构层次分解得到，自上而下逐步将主工作缸设计任务分为部件级、组件级直至零件级任务，在本文定义下，零件级任务即元任务，其中包括主缸体设计、主柱塞设计、柱塞导套设计、移动横梁设计等共27个设计活动单元，各活动单元名称及其指标参数信息如表7、表8所示。

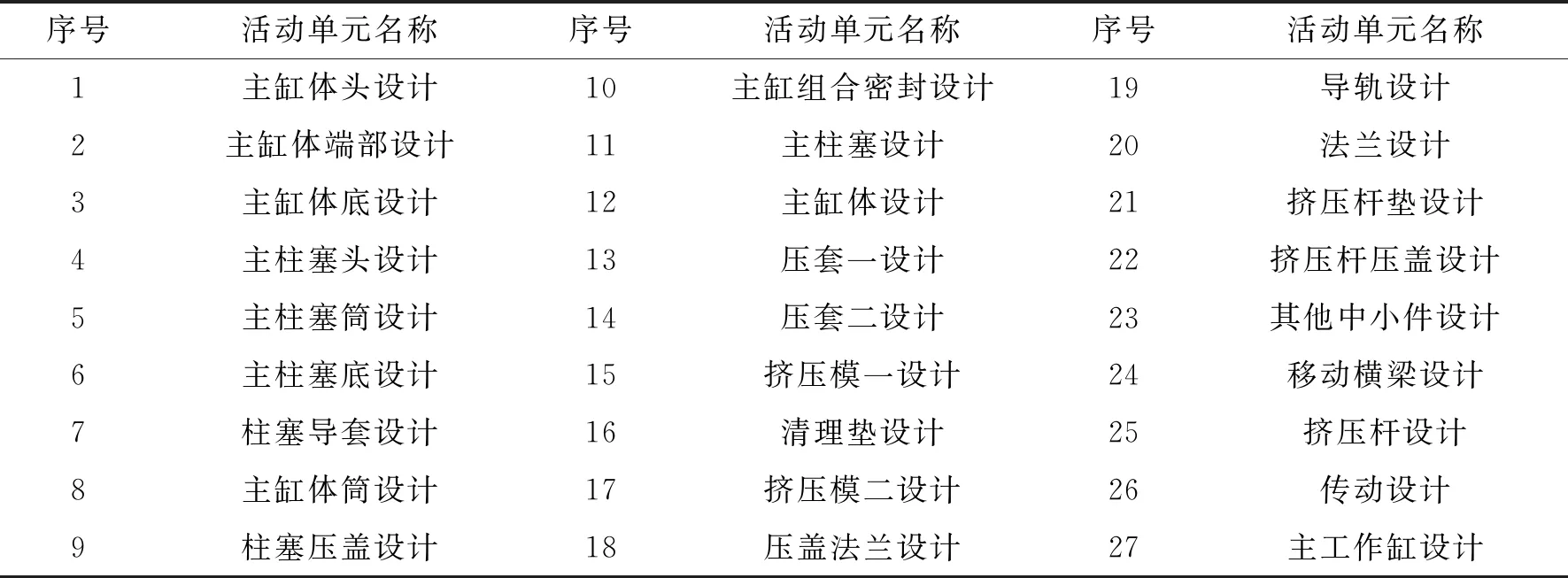
表7 125MN挤压机主工作缸设计项目活动单元名称

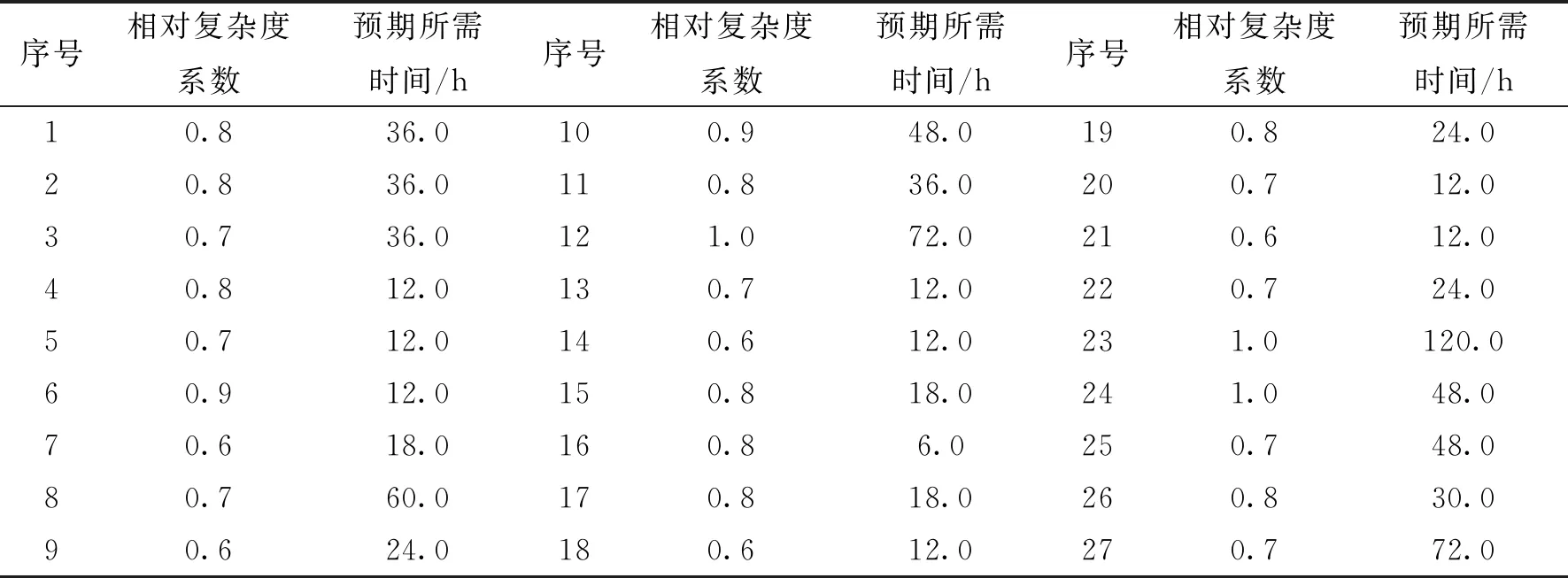
表8 活动单元指标参数信息

针对上述主缸设计项目，现有两种任务粒度设计方案A、B，其各自对应的任务分解集合，即子任务集如图6所示。

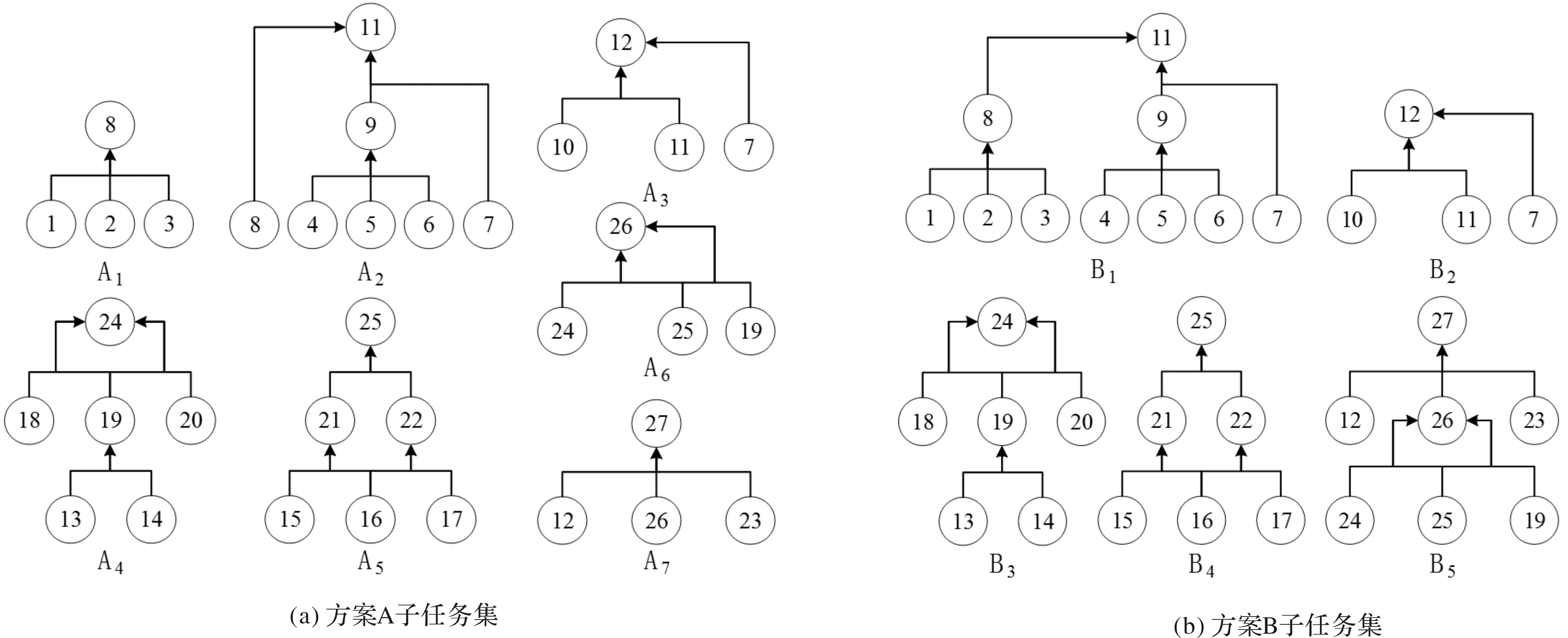
图6 备选方案子任务集

基于本文提出的任务粒度评价体系，对A、B两种方案分别进行评价。两种方案所对应的项目及各子任务有关参数值经计算如表9所示，其中任务耦合参数均设为0.5；负载影响因子设为等值。

表9 备选方案指标参数值

首先进行绝对性指标的评价，按照企业以往对于125 MN挤压机主工作缸定制项目的研发经验，这里设定项目任务粒度值阈值为0.05，平台资源水平定义为1。分别对两种方案的三类绝对性指标进行计算和评价，评价结果如表10所示。

表10 绝对性指标评价

从三类绝对性指标来看，两种方案均在指标的可行取值范围内或满足约束条件，故认为A、B两种方案均为可行方案，但哪一方案的任务粒度设计更优还需要进行相对性指标的评价。

分别对两种方案的任务内聚系数、任务耦合系数、项目耦合/内聚系数比率等相对性指标参数进行计算，并根据计算结果对两种方案进行评价，评价结果如表11所示。

表11 相对性指标评价

对于任务内聚性指标，方案A和方案B的任务内聚系数分别为0.110和0.196，从指标参数来看，方案B的任务内聚性更好，综合以往设计经验赋予“优秀”评级；而方案A任务内聚性相对较差，综合以往设计经验赋予“一般”评级。

同样地，其余相对性指标均按照上述流程进行评价，得到两方案对应的评价结果，并依照表6对各方案对应指标进行打分，这里统一取评级区间的上限，例如“优秀”评级即对应1分。进而基于式(23)对两方案对应的任务粒度合理性综合评分进行计算，最终得到方案A得分为0.685，方案B得分为0.762。显然，从任务粒度合理性得分来看，方案B更好，处于“良好”评级，说明方案B对应的任务分解方案得到的任务粒度更加合适，更符合网络化协同制造模式情境，但同时该方案并没有达到“优秀”评级，仍存在可以优化的地方。上述结果同企业生产实际情况相符，目前企业同样是以方案B作为主缸项目的任务粒度设计方案，说明了本文建立的任务粒度评价模型具有一定的准确性。

5 结论

本文针对复杂重型装备网络化协同制造模式下任务分解环节中的任务粒度评价流程展开研究，本文的主要成果如下：

(1)以复杂重型装备网络化协同制造模式为对象，对该模式下的项目实施流程进行了分析，归纳了其主要特征以及在任务粒度评价环节存在的问题。

(2)基于系统性、合理性、关键性的构建原则，构建了一套复杂重型装备网络化协同制造任务粒度评价指标体系。该体系按绝对性指标、相对性指标进行划分，从子任务和项目两个维度出发，对任务分解后的任务粒度结果分别以任务粒度大小、任务可行性、任务完整性等8个指标进行了评价，并以基于AHP-RS的组合权重计算法为体系中的相对性指标计算了权重，为复杂重型装备网络化协同制造模式下任务粒度的评价提供了一种新的解决思路。

(3)以某125 MN挤压机主工作缸研发设计项目为例，对本文提出的任务粒度评价方法进行了应用，应用结果验证了该方法的可行性和有效性。

由于复杂重型装备网络化协同制造模式过程复杂，所涉及的流程繁杂且各环节直接交互性强，故在该模式下的任务分解所涉及的环节以及考虑因素也较多，相应的对于任务分解结果的评价也涉及诸多方面。本文主要对该模式下任务分解结果对应的任务粒度合理性评价进行了研究，如何以更加广泛的视角对该模式下的整个任务分解过程进行更加全面的评价，以此确保整个任务分解环节的合理性，是后续需要进一步拓展和研究的重点内容。