多源多层的融合自适应加权积分旋翼无人机测高算法

黄 鹤,谢飞宇,王会峰,王 珺,杨 澜,茹 锋

(1.长安大学 西安市智慧高速公路信息融合与控制重点实验室,陕西 西安 710064;2.长安大学 电子与控制工程学院,陕西 西安 710064;3.长安大学信息工程学院,陕西西安 710064)

无人航行器技术已获得快速发展[1],无人航行器通过携带多传感器对外界数据进行采集,利用智能算法进行自主决策,进而完成所需任务。其中,测高技术是无人机(Unmanned Aerial Vehicle,UAV)智能检测的重要环节,在空域较大的情况下,要使旋翼无人机稳定完成低空区域的自主巡航和悬停定位,需要高精度的测高技术做保证。传感器系统为无人机测高提供数据支持,一般包括GPS、无线电高度表、气压高度计和加速度计等[2]。选择更优的融合估计算法是多传感器融合效果更佳的关键[3-5],现有融合估计算法可分为两类。一类方法是针对观测信息中的噪声误差,建立适合工程需求的系统误差参数模型,采用矢量扩维的方法直接转化为标准形式下的状态融合估计问题[6]。这类方法过度依赖关联概率分布、先验概率分布、噪声强度等先验知识,在实际的无人机测高过程中,由于环境影响未知,因此不可行。另一类方法是通过挖掘数据之间的可靠性信息,确定融合估计权重[7]。但是随着测量次数的增加,数据量有所增加,新数据会不可避免地受到陈旧信息的影响逐渐失去修正能力,融合估计效果较差。针对以上方法的不足,在测量误差无先验信息的情况下,本文提出了一种基于相关认知支持度的多传感器融合自适应加权积分算法,并设计了多源多层信息融合旋翼无人机测高算法,克服了现有测高算法需要运用陈旧信息的局限性。在融合加权后使用自适应互补滤波方法,无需过多的先验知识和噪声特性,相对于卡尔曼滤波方法,在精度和稳定性方面都有较大提升。

本文所使用的无人机测高系统的结构如图1所示,算法过程可分为3步:

图1 无人机测高系统的结构Fig.1 Structure of UAV altimetry system

(1)利用搭载多传感器的无人机系统采集不同时刻气压计和GPS的数据,设计相关认知支持度对数据进行预处理,将某些传感器发生故障或由环境因素产生较大偏差的测量数据去除掉;

(2)设计融合加权算法对每一时刻数据的权值运算得到初步的测高结果;

(3)设计辅助测高模块,采用加速度计传感器组建自适应滤波模型,进一步减弱干扰噪声,提高无人机测高数据的精度和可靠性。

1 基于相关认知支持度的一致性度量

假设多传感器系统包括m个相互独立的传感器,对静止或渐变参数直接测量,测量方程可表示为

若ri(k)越大,则在k时刻,第i个传感器与其他传感器对真值X的认知程度越高;若ri(k)越小,则在k时刻,第i个传感器与其他传感器对真值X的认知程度越低。随着测量次数和时间k的变化,通过ri(k)来判断第i个传感器的可靠性。

2 多源多层融合自适应加权积分测高算法

2.1 融合自适应加权的总体框架

旋翼无人机测高模型由两层信息融合算法组成,其总体框图如图2所示。我们提出的基于相关认知支持度的多源多层数据融合加权积分算法为第一子层。自适应互补滤波为第二子层[8]。

图2 融合自适应加权积分算法的总体框图Fig.2 Overall block diagram of fusion adaptive weighted integration algorithm

在正常情况下,无人机在高空悬停测高时,GPS和气压计测量数据所受到噪声的影响都不大,基本会保持在真实高度值附近轻微波动,数据稳定。而加速度计的测量数据噪声较小,对其经过两次积分,就可以基本转化为真实情况下的高度。但长时间的积分会累积误差,造成积分漂移。结合3个传感器各自的特点,需将GPS和气压计的测量数据进行一次加权融合,再与加速度计的测量数据进行二次数据融合作为辅助测高。在工作时间比较长时,融合加权GPS和气压计的数据结果,不断修正加速度计中累计的积分值,有效解决漂移现象导致的积分误差。在噪声较大的情况下,会不可避免地出现尖锐的毛刺,为了将这些毛刺彻底滤除,设计了自适应互补滤波作为第二层数据融合。这样既实现了无先验条件下的无人机测高,又避免了测量时间累加带来的积分漂移,具有良好的测高效果。

2.2 多源数据加权积分融合算法

在第一层融合中,针对测高时多种传感器、噪声统计特性的不确定,设计了一种基于相关认知支持度的多源数据加权积分融合算法。首先,利用一致性检验理论对所有传感器测量数据进行预处理,去除多传感器系统中受某些传感器故障或环境因素影响产生的较大偏差的测量数据,然后将各个传感器在不同时刻与之前相邻时刻的测量值进行融合,利用时间递推理论估计得到第一次融合结果。这样可以消除由于单个传感器在实际工程中测量的不确定性,提高测量结果的准确性。第一层融合的过程如图3所示。

图3 第一层融合的框图Fig.3 Block diagram of the first layer fusion

若全部利用一致性序列ri(k)的信息,前一时刻的权重结果将影响后一时刻的权值分配,这会造成大量陈旧信息的累积。同时,前一时刻数据出错也会影响后一时刻数据预测的准确性,导致数据出现整体错误。对于无人机测高算法来说,当前时刻传感器获得的高度测量数据所包含的信息,比过去时刻所包含的信息价值更大。而多源数据加权积分融合应使得当前测量数据的信息利用程度最大化、最优化,尽可能发挥当前时刻数据的优势。本文对于多源数据加权积分融合算法中的权重取值,只考虑当前k时刻的ri(k)以及k-1时刻的ri(k-1),完全可以避免k-1时刻之前的陈旧信息的干扰。

考虑k时刻第i个传感器的一致性度量ri(k)所占的比重对融合结果的影响,取k和k-1时刻的一致性度量ri(k)和ri(k-1)的平均值作为当前时刻融合的均值权重Wj(k),公式如下:

可以看出,整个融合算法权重的选取完全来自传感器网络测量数据本身,避免了主观选择融合参数所带来的不确定性,具有良好的自我调节能力。

2.3 第二层融合

在第二层融合中设计了自适应互补滤波方法,如图4所示。加速度计的数据能够对测高起到较好的辅助作用。同时,长时间工作时,GPS和气压计测量融合数据能够把加速度计积分值导致的误差不断修正,可以有效解决积分漂移的问题。

图4 第二层融合的框图Fig.4 Block diagram of the second layer fusion

3 实验结果

实际上,在悬停过程中,允许四旋翼无人机有水平方向的细微侧滑调整。在不失通用性的前提下,构建了以下试验环境,如图5所示。数据采集使用F450四旋翼飞行器机架,搭载MS5611气压计和M8N GPS;飞控设备使用Pixhawk开源飞控,搭载STM32F427核心处理芯片和STM32F103故障协同处理芯片。实验过程中各采集150组不同高度的数据进行分析。无人机高度数据是在西安市某两栋高层建筑的顶部获得的,共采集两组不同的高度数据,实测屋顶天台相对于地面高度h1为228 m和299 m,h2为2 m和1 m。试验杆竖直固定在屋顶上,连接水平的金属杆,直接从天台伸出面向地面。无人机悬挂在杆下导轨上面对地面可以进行横向滑动,保证相对于地面的准确高度始终不变。高度融合信息处理的硬件平台使用Intel Core i7-11800H 2.3 GHz CPU,16 G内存的计算机,通过对试验获取的高度数据进行计算分析,并使用MATLAB R2021a软件平台进行融合验证,证明了本文方法的有效性。

图5 测高场景图Fig.5 Altimetry scene diagram

将MPU6050的三轴微电子机械系统(Micro-Electro-Mechanical System,MEMS)数字加速度计作为本次试验设备,其校准首先放置在水平面上,Z轴向下进行X,Y轴零位校准,然后以X轴旋转90°再进行Z轴零位校准。加速度计在静止状态下,Zg(在静止时,Zg为负数,对应的数据是重力加速度g)是Z轴上所得到的数据。加速度计测量得到的加速度数据、速度数据、高度数据如图6～图8所示,从中可以看出数据不够稳定,但误差较小。由于旋翼无人机在飞行过程中的震动以及长时间工作,会导致加速度计芯片自身的温度变化,加速度计传感器在长时间测量且没有其他传感器对数据进行修正的情况下,积分不断累计会导致漂移现象,因此只能将其作为辅助测高数据。

图6 加速度计测量的加速度曲线Fig.6 Acceleration curve measured by accelerometer

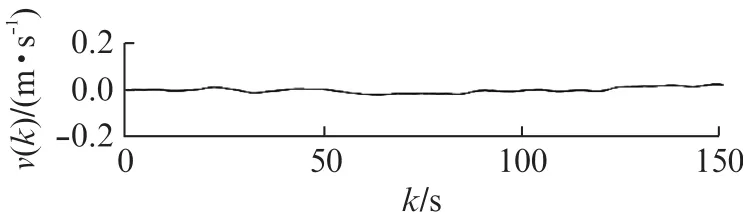
图7 加速度计测量的速度曲线Fig.7 Velocity curve measured by accelerometer

图8 加速度计测量的高度曲线Fig.8 Height curve measured by accelerometer

图9为一致性序列曲线。实验高度为230 m和300 m的多种方式测高所得的高度曲线如图10所示,其误差曲线如图11所示。根据仿真结果,气压计和GPS测量高度曲线存在较大误差。经过融合加权后,可以看出,获得的数据在实测高度值上下存在轻微波动,但测量数据比较稳定,并且高度误差明显低于单个传感器测得的误差。经过自适应互补滤波后,误差进一步减小,精度进一步提高。

图9 一致性序列曲线Fig.9 Consistent sequence curve

图10 多种方式测高的高度曲线Fig.10 Height curves of height measurement in various ways

由图11可以看出,从单个传感器到融合加权高度、自适应互补滤波的设计,测得的高度误差逐渐减小,测量精度和稳定性进一步提高。本文采用的自适应互补滤波方法与文献[8]的滤波方法相比,在无需任何先验知识的情况下,均方根误差(Emean)和最大误差(Emax)都更小,因此该方法速度更快且精度更高、稳定性更好,结果见表1(见第 458页)。

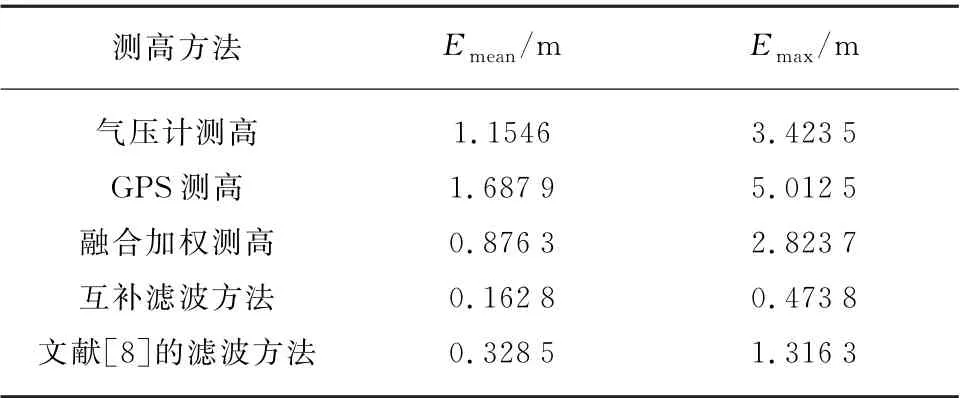
表1 实验结果评价指标Tab.1 Evaluation of experimental results

图11 多种方式测高的高度误差曲线Fig.11 Height error curves of height measurement in various ways

为了进一步验证实验效果,将本文的测高系统与自适应卡尔曼滤波测高系统、文献[9]的基于自适应S滤波无人机高度融合估计系统以及文献[10]的二步延迟自适应时空融合测高系统进行测高的效果对比,具体误差数据见表2(见第 458页)。图12(见第 458页)为各测高系统的误差曲线对比,结合表2,可以看出,虽然文献[10]中的测高方法的精度略低于本文方法,但该方法在测高开始时有较大的波动,测得结果不够稳定。而本文系统相对于其他2种测高系统来说,效果明显更好,误差更低。

图12 测高系统的误差曲线对比Fig.12 Comparison of altimetry system error curves

表2 测高系统误差数据对比Tab.2 Comparison of altimetry system error data

4 结 语

本文设计了一种多源多层融合自适应加权积分旋翼无人机测高算法,算法包含第一层加权积分融合和第二层自适应互补滤波融合,利用GPS和气压计的测量数据对加速度计的误差不断进行修复,提高了无人机的定高精度。系统对于先前经验概率分布知识和噪声特性的要求不高,且无人机状态参数的测量不同于雷达,数据量很小,整个系统的计算量不大,应用价值明显。