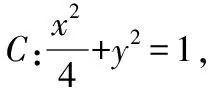教学考试杂志社“数学经典试题及变式”征集活动阶段性成果展示
2022-08-30韩兆峰,彭长军,赵伟娜等
一、直线与圆的综合应用
吉林 韩兆峰
【母题1】(多选题)(2021·新高考Ⅰ卷·11)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则( )
A.点P到直线AB的距离小于10
B.点P到直线AB的距离大于2
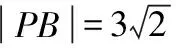
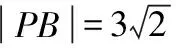
【试题分析】考查知识:直线与圆的位置关系及两点间距离;解题方法:借助图形分析建立“形”与“数”的联系,采用数形结合的思想;综合素养:数学运算及数学建模核心素养.
【答案】ACD
甘肃 彭长军
【变式1】(知识变式)求点到直线的距离的最值变为求三角形面积的最值
已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则△PAB的面积的最大值为________,最小值为________.

河北 赵伟娜
【变式2】(知识变式)直线的方程含有参数,直线变为过定点的动直线
(2022·高三模拟试题·11)(多选题)已知圆C:x2+y2-6x-8y+21=0和直线l:kx-y+3-4k=0,则( )
A.直线l与圆C的位置关系无法判定

C.当圆C上有且仅有3个点到直线l的距离等于1时,k=0
D.如果直线l与圆C相交于M,N两点,则M,N的中点的轨迹是一个圆
【答案】BC
吉林 韩兆峰
【变式3】(知识变式)由求点到直线距离变为求圆的方程
(改编)已知圆M:(x-5)2+(y-5)2=16,若点A(4,0),B(0,2),那么与⊙M关于直线AB对称的⊙N的方程是________.

吉林 韩兆峰
【变式4】(方法变式)由求点到直线距离变为求参数的范围
(改编)已知圆M:(x-5)2+(y-5)2=16,设点T(t,0),圆M上存在一点P使∠MTP=30°,则t的取值范围是________.
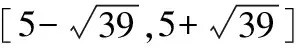
甘肃 彭长军
【变式5】(方法变式)求切线长变为求过圆内定点的最短弦长及最短弦所在直线的方程
已知圆C:(x-5)2+(y-5)2=16和直线l:(m+2n)x+(m-n)y-8m-10n=0(m,n∈R),求直线l被圆C所截得的最短弦的长度及最短弦所在直线的方程.
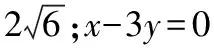
河北 赵伟娜
【变式6】(素养变式)曲线方程复杂化,落实逻辑推理的数学核心素养

A.曲线C表示两条直线
B.当r=4时,曲线C与圆M有2个公共点
C.当r=2时,存在圆N,使得圆N与圆M相切且圆N与曲线C有4个公共点
D.当曲线C与圆M的公共点最多时,r的取值范围是(4,+∞)
【答案】AC
安徽 王玉佩 张超
【母题2】(2020·全国卷Ⅰ理·11)已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( )
A.2x-y-1=0 B.2x+y-1=0
C.2x-y+1=0 D.2x+y+1=0
【试题分析】考查知识:直线与圆的位置关系及面积相关知识;解题方法:数形结合、化归与转化思想;综合素养:直观想象、数学运算、逻辑推理等数学核心素养.
【答案】D
江西 叶新波
【变式1】(知识变式)求直线方程变为求长度、角度范围及直线过定点问题
(多选题)已知圆M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,过点P作圆M的切线PA,PB,切点为A,B,则( )

B.存在点P,使得∠APB=90°
C.直线AB经过一个定点
D.线段AB的中点在一个定圆上
【答案】BCD
安徽 王玉佩 张超
【变式2】(方法变式)基于点到直线距离公式进一步求方程
已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,过点P作⊙M的切线PA,PB,切点为A,B,当M到直线AB的距离最大时,直线AB的方程为( )
A.2x-y-1=0 B.2x+y-1=0
C.2x-y+1=0 D.2x+y+1=0
【答案】D
甘肃 彭长军
【变式3】(方法变式)通过|PM|·|AB|取得最小值的条件进一步探寻切点弦,求△QAB的面积的最大值
已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,Q为⊙M上的动点.过点P作⊙M的切线PA,PB,切点为A,B.当|PM|·|AB|最小时,△QAB的面积的最大值为________.

江西 叶新波
【变式4】(素养变式)融入参数方程,处理数量积和面积问题
已知点A(2,0),B(0,2)和点P(cosθ,sinθ),θ∈R.给出下列四个结论:

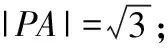
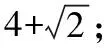

其中所有正确结论的序号是________.
【答案】①②④
安徽 王玉佩 张超
【变式5】(素养变式)融入距离和绝对值函数
已知⊙M:x2+y2-4x-2y+1=0,直线l:2x+y+2=0,P为y轴上的动点,过点P作⊙M的切线PA,PB,切点为A,B,切线长为d1.设点P到直线l的距离为d2,当d1+d2取最小值时,P的纵坐标为( )
【答案】A
二、圆锥曲线的几何性质
甘肃 彭长军

【试题分析】考查知识:椭圆的标准方程与性质,直线与圆的位置关系及简单几何性质,点到直线的距离公式以及点与曲线的位置关系等;解题方法:推理运算及数形结合思想;综合素养:数学运算及逻辑推理核心素养.

甘肃 彭长军
【变式1】(知识变式)把圆换成抛物线


甘肃 彭长军
【变式2】(知识变式)把直线与圆相切变为直线被圆截得的弦长为c


甘肃 彭长军
【变式3】(知识变式)把椭圆换成双曲线


甘肃 彭长军
【变式4】(素养变式)把直线与圆相切变为直线与圆相交,把求斜率及离心率的值变为求其范围


安徽 朱益

【试题分析】考查知识:圆锥曲线的几何性质与平面几何知识综合;解题方法:数形结合思想;综合素养:数学运算与逻辑推理核心素养.
【答案】D
安徽 朱益
【变式1】(知识变式)定点变为动点
【答案】D
陕西 韩红军
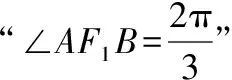

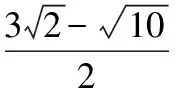
陕西 韩红军
【变式3】(知识变式)“AF⊥BF”变成“MF1⊥MF2”

【答案】D
河北 赵伟娜
【变式4】(知识变式)将垂直(90°)变为120°
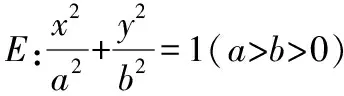
【答案】C
安徽 朱益
【变式5】(方法变式)巧用平面几何知识,化繁为简

【答案】A
河南 赵先举
【变式6】(方法变式)基于椭圆的定义融入椭圆的对称性

陕西 韩红军

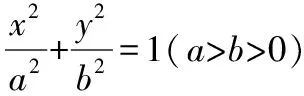

陕西 韩红军
【变式8】(素养变式)“AF⊥BF”变成“sin∠ABF1≤2sin∠BAF1”


安徽 吴志勇
【母题3】(2016·全国卷Ⅲ理·20节选)已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.若点F在线段AB上,R是PQ的中点,证明:AR∥FQ.
【试题分析】考查知识:抛物线定义与性质、直线与抛物线位置关系;解题方法:过焦点弦直线AB满足yAyB=-p2.将直线AR和直线FQ的斜率用A或B的坐标表示,证明斜率相等.综合素养:考查逻辑思维能力、以及对设而不求解题思想的应用能力.
【答案】证明过程略
甘肃 彭长军
【变式1】(知识变式)基于抛物线的定义变式
已知抛物线C:y2=2px(p>0)的焦点为F,直线l过点F与抛物线交于A,B两点,A,B在准线上的射影分别为P,Q,连接PF,QF分别交y轴于G,H,连结AG并延长交准线于M,证明:M,H,B三点共线.
【答案】证明过程略
安徽 吴志勇
【变式2】(知识变式)将向量知识与抛物线几何性质相结合是本题的命题思想

【答案】3
安徽 吴志勇
【变式3】(方法变式)光学与焦点弦性质探究
已知抛物线C:y2=2x的焦点为F,直线AB经过抛物线的焦点F,且与抛物线交于A,B两点,过A,B两点分别作x轴的平行线交抛物线准线于P,Q两点.若准线上存在一点R,满足AR∥FQ,证明:AR⊥PF.
【答案】证明过程略
安徽 吴志勇
【变式4】(素养变式)判别式法与复合函数求斜率相结合
已知抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1与C交于A,B两点,过点A的直线l2交C于另一点D,交x轴的正半轴于点E,且|FA|=|FE|.若抛物线C在点B处的切线为l3,证明:l2∥l3.
【答案】证明过程略
江西 邹荣华

(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB
【试题分析】考查知识:椭圆的定义与性质;解题方法:通过直线与圆锥曲线联立建立直线斜率关系,运用通性通法解决问题,综合素养:数学运算与逻辑推理核心素养.

(2)证明过程略
河南 赵先举
【变式1】(知识变式)圆锥曲线变为抛物线

(1)求抛物线C的方程;
(2)当直线AB变动时,x轴上是否存在点Q,使得∠AQP=∠BQP,若存在,求出点Q坐标;若不存在,说明理由.
【答案】(1)y2=2x;
(2)x轴上存在点Q(-2,0),使得∠AQP=∠BQP
江西 邹荣华
【变式2】(知识变式)由角相等问题变为圆锥曲线中面积问题

【答案】证明过程略
甘肃 彭长军
【变式3】(方法变式)由角相等问题变为存在性问题


江西 邹荣华
【变式4】(方法变式)条件与结论互换

【答案】存在M(2,0),使∠OMA=∠OMB恒成立
河南 赵先举
【变式5】(素养变式)角度相等变为二倍角关系
(1)求椭圆C的方程;
(2)直线y=kx+m(km≠0)与椭圆C交于A,B两点,与y轴交于点P,线段AB的垂直平分线与AB交于点M,与y轴交于点N,O为坐标原点.如果∠MOP=2∠MNP成立,求k的值.

江西 邹荣华
【变式6】(素养变式)由角相等问题变为定值定点问题


三、圆锥曲线定点与定值问题
河北 赵伟娜
【母题1】(原创)已知抛物线y2=16x,若不过原点O的动直线l与抛物线交于M,N两点,且OM⊥ON,则直线l过定点________.
【试题分析】考查知识:直线与抛物线位置关系;解题方法:方程思想的应用;综合素养:数学运算与逻辑推理核心素养.
【答案】(16,0)
江西 邹荣华
【变式1】(知识变式)类比母题更换已知条件进行变式
已知抛物线C:y2=16x,不过坐标原点O的动直线l与抛物线C交于M,N两点,P在线段MN上,若OP⊥MN且|OP|2=|PM||PN|,直线MN是否过x轴上的定点?若是求出定点,若不是说明理由.
【答案】直线MN经过x轴上的定点(16,0)
河北 赵伟娜
【变式2】(知识变式)先有定值再求定点
(原创)已知抛物线y2=16x,过原点O作两条直线l1,l2,分别与抛物线交于M,N两点,且l1,l2的斜率k1,k2满足k1·k2=2,则直线MN过定点________.
【答案】(-8,0)
甘肃 彭长军
【变式3】(知识变式)先过定点再求定点
过抛物线C:y2=16x的焦点F的直线l交抛物线C于A,B两点且直线l与x轴不垂直,若A关于x轴的对称点为D,求证:直线BD过定点,并求出该点的坐标.
【答案】直线BD恒过点(-4,0)
河北 赵伟娜
【变式4】(方法变式)先过定点再求定值
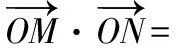
【答案】-48
广东 周艳祖
【变式5】(方法变式)换斜率积为和
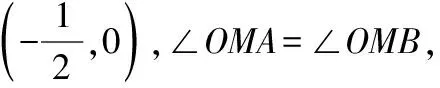
【答案】证明过程略
辽宁 蔡明天
【变式6】(素养变式)原点变式为抛物线上普通点
(改编)抛物线C的方程为:x2=8y,点P(4,2),直线l与抛物线C交于异于点P的A,B两点,以线段AB为直径的圆经过点P.问:直线l是否过定点?若是,求出所过定点的坐标;若不是,请说明理由.
【答案】直线l过定点(-4,10)
辽宁 蔡明天
【变式7】(素养变式)直线过定点隐含到其他(本题是面积比)问题

(1)求椭圆C1的标准方程;



广东 周艳祖
【变式8】(素养变式)抛物线拓展到椭圆
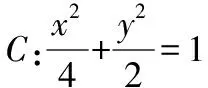
【解题策略】证明过程略
山东 李俊岭 刘慧
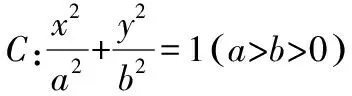
(1)求椭圆C的方程和离心率;
(2)过点P(4,0)且与x轴不重合的直线l与椭圆C交于A,B两点,与直线x=1交于点Q,点M满足MP⊥x轴,MB∥x轴,求直线MA的斜率与直线MQ的斜率的比值.
【试题分析】考查知识:椭圆的标准方程、离心率、直线与椭圆的位置关系、韦达定理、直线的斜率等知识;解题方法:坐标法、数形结合、化归与转化,由特殊到一般等数学思想方法的应用;综合素养:直观想象、数学运算、逻辑推理等数学素养.

山东 李俊岭 刘慧
【变式1】(知识变式)由椭圆背景到抛物线背景的变式
已知过点P(-1,0)且与x轴不重合的直线l与抛物线C:y2=4x交于A,B两点,与直线x=1交于点Q,过点B作BM⊥x轴,垂足为点M,求证:直线MQ与直线MA的斜率之比为定值.

山东 李俊岭 刘慧
【变式2】(知识变式)基于调合线束变化的变式
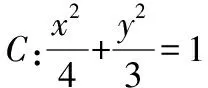
【答案】kAM+kBM=-1
山东 李俊岭 刘慧
【变式3】(方法变式)调换调和点列中的点确定点M
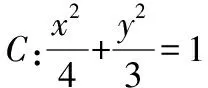

山东 李俊岭 刘慧
【变式4】(素养变式)对原问题进行逆向思考
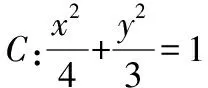
【答案】过定点(4,0)
山东 李俊岭 刘慧
【变式5】(素养变式)对原问题换一种问法
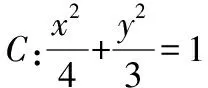
【答案】证明过程略
山西 李小丽
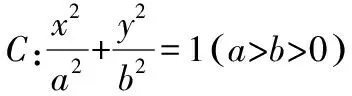
(1)求C的标准方程;
(2)过点P(0,1)的两条直线分别和C交于不同两点A,B(A,B异于点P且不关于坐标轴对称),直线PA,PB的斜率分别为k1,k2,且k1k2=1,试问直线AB是否恒过定点?若是,求出该定点的坐标;若不是,请说明理由.
【试题分析】考查知识:本题为圆锥曲线中的定值定点问题,属于综合问题,几乎考查圆锥曲线的所有知识;
解题方法:参数法(圆锥曲线的定点、定值问题会涉及到曲线上的动点及动直线,所以很常用的方法就是设动点或设动直线,即引入参数解决问题.设参数有两种情况,一种是设点的坐标,另一种是设直线的斜率);从特殊到一般法:(如果要解决的问题是一个定值或定点问题,而题设条件又没有给出这个定值或定点,那么我们可以这样思考:由于这个定值或定点对符合要求的特殊情况必然成立,那么我们可以根据特殊情况先找到这个定值或定点,明确了解决问题的目标,然后进行一般情况下的推理证明);
综合素养:本题考查数学抽象、逻辑推理、数学运算核心素养.

山西 李小丽
【变式1】(知识变式)将条件中的斜率之积改为斜率之和
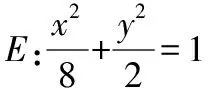
(1)当λ=1时,求证:直线l过定点,并求出定点坐标;
(2)当λ=0时,求证:直线l的斜率为定值,并求出定值

辽宁 蔡明天
【变式2】(知识变式)母题条件与结论可以互推,反序命题
(1)求椭圆C的方程;
(2)不过点P的直线l:y=kx+2与椭圆C交于A,B两点,记直线PA,PB的斜率分别为k1,k2,试判断k1+k2是否为定值.若是,求出该定值;若不是,请说明理由.

(2)k1+k2为定值,且k1+k2=3
甘肃 焦永垚
【变式3】(知识变式)斜率之积为定值变为斜率之和为定值
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.

河北 赵伟娜
【变式4】(知识变式)斜率关系复杂化,探究直线恒过的定点
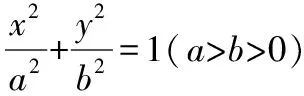
(1)求椭圆的标准方程;
(2)探究直线AB是否过定点,若过定点,求出定点坐标,若不过定点,请说明理由.

(2)直线AB恒过定点(-4,-3)
河北 赵伟娜
【变式5】(知识变式)变换曲线为抛物线,将条件转化为斜率关系探求直线恒过的定点
(2020·保定基础模拟考试·21)设抛物线C:y2=2px(p>0)的顶点到焦点的距离为1.
(1)求抛物线C的方程;
(2)设过点P(1,2)的直线l1,l2,分别与抛物线C交于M,N两点(不同于点P),以MN为直径的圆恰好经过点P,证明:直线MN经过定点,并求出该定点坐标.
【答案】(1)y2=4x;(2)直线MN经过定点(5,-2)
河北 赵伟娜
【变式6】(方法变式)变换待求结论,探究圆过的定点

(1)求椭圆C的方程;
(2)若直线AM,AN分别与直线x=4交于点P,Q,证明:以线段PQ为直径的圆恒过两个定点,并求出定点的坐标.

甘肃 董宏杰
【变式7】(素养变式)圆锥曲线定点问题中参变量关系的转化

(1)求E的方程;
(2)证明:直线CD过定点.
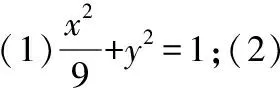
山西 李小丽
【变式8】(素养变式)结论变为计算三角形面积的最值