核心素养视角下的变式与拓展
——以一道课本习题为例
2022-08-30广东周艳祖
广东 周艳祖
高中数学教材中的许多例题、练习题、习题和复习参考题(简称“四题”)因为有着极强的“代表性”与“穿透性”,往往因受到命题者的青睐而成为高考的题源.2019年人教A版的习题分为“复习巩固”“综合运用”“拓广探索”三个层次,开展对教材习题的研究,创设合理的变式教学,以“最近发展区”为平台,拓展学生的认知,在落实“情境与问题、知识与技能、思维与表达、交流与反思”的过程中既夯实了学习以及未来发展所必需的“数学基础知识、基本技能、基本思想、基本活动经验”,又培养了学生的数学核心素养.
【源题】(2019年人教A版选择性必修第一册第138页习题3.3复习巩固第6题)直线y=x-2与抛物线y2=2x相交于A,B两点,求证:OA⊥OB.(详细解答过程略)
一、结论不变,改装已知条件
结论不变,将定直线变为过定点的动直线,让学生在运动、变化、发展中探索不变的元素与性质.
变式1:已知过点M(2,0)的直线与抛物线y2=2x相交于A,B两点,求证:OA⊥OB.
【解析】可设A(x1,y1),B(x2,y2),显然直线AB的斜率k≠0,则可设其方程为x=ty+2,将直线的方程代入到y2=2x,化简得y2-2ty-4=0,由韦达定理得
y1+y2=2t,y1y2=-4,
x1x2=(ty1+2)(ty2+2)=t2y1y2+2t(y1+y2)+4=4.
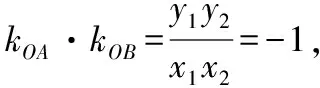
【评注】浅显易懂,将直线与抛物线的方程联立,运用韦达定理求出两根之和与积,是解决这一类相关问题的“通法通解”,思路清晰简洁,让学生进一步熟悉常规方法.
二、互换结论与条件,培养逆向思维
将变式1中的结论变为条件,用同样的方法与技巧去探索它们之间的关系,检验学生对方法的熟练程度,培养学生的逆向思维和未来发展所必需的数学素养.
变式2:设A,B是抛物线y2=2x上异于原点O的两点,且OA⊥OB,求证:弦AB过定点(2,0).
【解析】可设A(x1,y1),B(x2,y2),显然直线AB的斜率k≠0,则可设其方程为x=ty+m,将直线的方程代入到y2=2x,化简得y2-2ty-2m=0,由此得到
y1+y2=2t,y1y2=-2m,
x1x2=(ty1+m)(ty2+m)=t2y1y2+mt(y1+y2)+m2=m2.
因为OA⊥OB,所以kOA·kOB=-1,
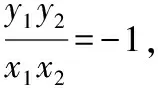
直线AB的方程为x=ty+2,
当y=0时,x=2,所以弦AB过定点(2,0).
【评注】基于学生思维的“最近发展区”,着重培养学生的数学运算与逻辑推理核心素养.
在变式1和变式2的基础上,归纳总结得到一般性的结论,由于证明过程有很大的相似性,此处不再做详细的证明.
结论1:设A,B是抛物线y2=2px上异于原点O的两点,若OA⊥OB,则弦AB过定点(2p,0),反之亦然.
三、变特殊角为任意角,培养发散思维
变特殊角为任意角,在斜率积为定值的条件下,探索直线的斜率积与过定点之间的关系,进一步推广已有的结论.
变式3:设A,B是抛物线y2=2x上异于原点O的两点,且kOA·kOB=-2,求证:弦AB过定点(1,0).
路径1(常规解法):可设A(x1,y1),B(x2,y2),显然直线AB的斜率k≠0,
则可设其方程为x=ty+m,
将直线的方程代入到y2=2x,化简得
y2-2ty-2m=0,由韦达定理得
y1+y2=2t,y1y2=-2m,
x1x2=(ty1+m)(ty2+m)=t2y1y2+mt(y1+y2)+m2=m2.
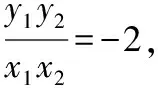
解得m=1或m=0(舍去),
直线AB的方程为x=ty+1,
当y=0时,x=1,所以弦AB过定点(1,0).
【评注】将两条互相垂直的直线变为成任意角的两条相交直线,既检验学生对方法的熟练程度,又可以培养学生的发散思维.
路径2(齐次化):可设A(x1,y1),B(x2,y2),
直线AB的方程为mx+ny=1,
将直线的方程与抛物线的方程联立,
即y2=2(mx+ny)x,
化简得y2-2mx2-2nxy=0,
两边同时除以x2,
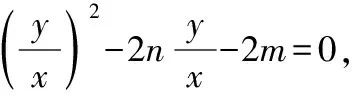
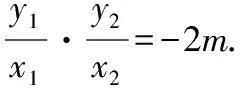
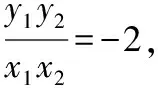
解得m=1所以直线AB的方程为x+ny=1,
当y=0时,x=1,因此弦AB过定点(1,0).
【评注】这种方法基于“整体的思想”下应用韦达定理,与路径1相比,运算量大大减少,由此可见齐次化的方法在解决圆锥曲线的双斜率模型问题的强大功效,往往可以事半功倍,当然在处理过程中也要有一定的技巧性,比如:将直线的方程设为mx+ny=1,联立时将系数“2”变换为“2mx+2ny”,这些都为后面的齐次化扫清了障碍.
变式4:过点M(1,0)的直线与抛物线y2=2x相交于A,B两点,求证:kOA·kOB=-2.
【评注】将变式3的条件与结论互换,由于证明过程有很大的相似性,此处不再做详细的证明,目的是培养学生的数学抽象核心素养.
在变式3和变式4的基础上,归纳总结得到一般性的结论,由于证明过程有很大的相似性,此处不再做详细的证明.
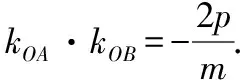
四、换斜率积为和,变式更丰富
将已知条件中斜率积为定值变成斜率和为零,让学生在新情境下探索直线过定点与斜率的关系,培养学生利用已有经验获得新知识的能力,进一步夯实数学学习所必需的“数学基础知识、基本技能、基本思想、基本活动经验”.

路径1(常规解法):可设A(x1,y1),B(x2,y2),
显然直线AB的斜率k≠0,
将直线的方程代入到y2=2x,
化简得y2-2ty-1=0,由韦达定理得
y1+y2=2t,y1y2=-1,

因为kMA+kMB=0,所以∠OMA=∠OMB.
【评注】表面上求角度相等,实质上可化归与转化为斜率和问题.将斜率和为零的问题“包装”为角度相等问题,在新情境下解决旧问题,本质是方程的联立与韦达定理的应用,进而求出斜率和.

可设A(x1,y1),B(x2,y2),
因为直线AB过点(1,0),
则直线AB的方程为x+ny=1,
将直线的方程与抛物线的方程联立,
即y2=2(x+ny)x-(x+ny)2,
化简得(1+n2)y2-x2=0,两边同时除以x2,
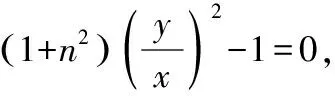
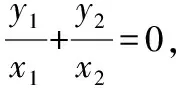
因为平移不会改变斜率的值,
所以kMA+kMB=0,所以∠OMA=∠OMB.
【评注】先平移再做齐次化,减少了运算量,方便了计算,提高了解题速度,但也有一定的技巧性.
在变式5的基础上,归纳总结得到一般性的结论,由于证明过程有很大的相似性,此处不再做详细的证明.

推论3.1:已知过点N(a,0)(a>0)的直线与抛物线y2=2px相交于A,B两点,点M的坐标为(-a,0),O为坐标原点,则∠OMA=∠OMB.
五、与椭圆和双曲线结合,变式更精彩
由于椭圆、双曲线和抛物线都是二次曲线,通过设计有层次性的变式训练的方式类比横向拓展这些性质,探索椭圆、双曲线是否有类似结论?
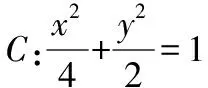
【评注】该变式与题源非常相似,此处不做详细解析.
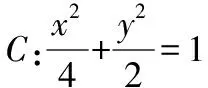

即(x+2)2+2y2=4,
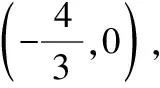

将直线的方程与椭圆的方程联立,
即2y2+x2-(3x+3ny)x=0,
化简得2y2-2x2-3nxy=0,两边同时除以2x2,

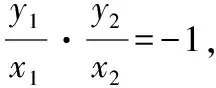
因为平移不会改变斜率的值,
所以kMA·kMB=-1,所以MA⊥MB.
【评注】先平移再做齐次化,减少了运算量,给解题带来了很大的方便.
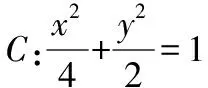
在变式7和变式8的基础上,归纳总结得到一般性的结论,由于证明过程有很大的相似性,此处不再做详细的证明.
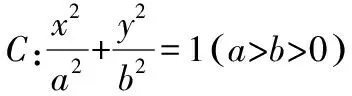
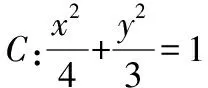
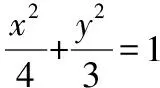
即4y2+3x2+24x+36=0,
因为直线AB过点(-3,0),
则直线AB的方程为x+ny=-3,
将直线的方程与椭圆的方程联立,
即4y2+3x2-(8x+8ny)x+4(x+ny)2=0,
化简得(4+4n2)y2-x2=0,两边同时除以x2,
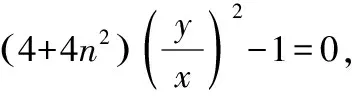
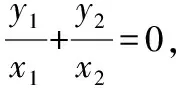
因为平移不会改变斜率的值,
所以kMA+kMB=0,所以∠OMA=∠OMB.
在变式9的基础上,归纳总结得到一般性的结论,由于证明过程有很大的相似性,此处不再做详细的证明.
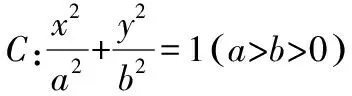
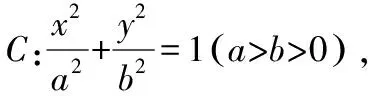
继续追问学生双曲线是否有类似性质,经探索得到如下结论:
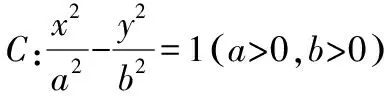
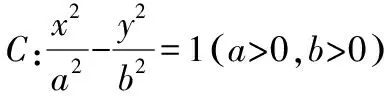
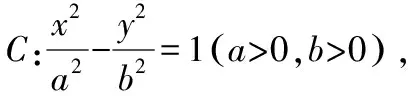
六、应用结论,链接考题
【例1】(2019·湖南高三月考理·16)已知F是抛物线y2=4x的焦点,点A,B在抛物线上且位于x轴的两侧,kOA·kOB=-2,其中O为坐标原点,则△AOB面积的最小值是.
【解析】设A(x1,y1),B(x2,y2),
由前面的结论2可知直线AB过定点(2,0),
显然直线AB的斜率k≠0,
则可设其方程为x=ty+2,
将直线的方程代入到y2=4x,
化简得y2-4ty-8=0,由韦达定理得
y1+y2=4t,y1y2=-8.


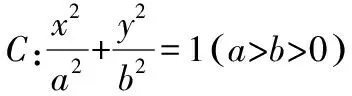
(1)求椭圆C的标准方程;
(2)设椭圆的右顶点为A,过椭圆长轴上一点N(t,0)作直线l,直线l与椭圆交于P,Q两点,若AP⊥AQ,求t的值.

七、变式教学与培养学生数学核心素养的思考

