基于微惯性测量单元的矿用定向钻孔轨迹绘制*

2022-08-30李海英

传感器与微系统 2022年8期

姚星,李海英

(上海理工大学机械工程学院，上海 200093)

0 引言

随着中国经济的快速发展，煤炭的需求也日益增加，煤炭的开采面临新的更高的要求。矿用定向钻机在瓦斯抽采、探水以及煤层走势勘探等方面具有重要作用[1]。为实现精确的定向钻机轨迹绘制，更好实现瓦斯抽采、煤层勘探效果，需要用到随钻测量(measurement-while-drilling,MWD)技术。MWD是指在钻井作业中实时确定底部钻具组合(bottom hole assembly,BHA)的位置和方向，是定向钻井中的一种重要工具。目前国外的MWD系统远远领先于国内[2]。20世纪70年代，Russell A W等人在其专利[3]中提出基于三轴正交加速度传感器与三轴正交磁传感器组合的姿态测量单元解算姿态。由于磁力计易受到周围磁场的干扰，如果采用能隔磁的无磁钻铤，则会大大增加成本且使用不方便[4]。

加速度计与陀螺仪组合构成的惯性导航系统(inertial navigation system,INS)不受磁场干扰，因此被引入MWD进行钻具的姿态测量。Noureldin H首先在文献[5]中提出将光纤陀螺(fiber-optic gyro,FOG)应用于石油钻井中油气田勘探的MWD。文献[6]在理论研究的基础上，采用基于INS的机械陀螺仪与加速度计组合进行钻具姿态测量实验，得到的结果表明，使用机械陀螺仪的姿态测量效果远优于使用磁力计时的结果。机械陀螺仪的使用会有体积限制与能耗过大的问题，因此，体积小、功耗低是未来MWD的发展方向。随着芯片技术与微机械电子技术(micro-electrical-mechanical system,MEMS)的发展，微传感器组合的测量单元因体积小、功耗低且抗干扰能力强等众多优点，被安装在细小的钻杆中。

MEMS惯性传感器含有运动单元，且本身尺寸较小，易受外部环境干扰，通常会存在误差。文献[6]采用了非平稳静止对准法(in drilling alignment,IDA)，文献[7]采用了旋转调制装置，均取得了较好的误差消除结果。以上两种方法均为精细误差消除，需要在实验室条件下做大量测试，建立误差模型。

本文采用数理统计分析方法，找出实验测量数据的统计规律，得到测量单元误差的有规律与随机漂移量分别进行消除，可适用于不同环境下的误差分析。本文用集成陀螺仪、加速度计的微惯性测量模块MPU6050进行姿态参数获取，通过STM32进行数据读取与处理，输出钻孔轨迹绘制所需的倾角与方位角等数据，在消除误差后绘制钻机的钻进轨迹。

1 钻孔轨迹绘制理论

钻孔的实际轨迹是钻头在钻进过程中钻杆留下的路径。实测轨迹是以实际测量得到的点为基础绘制的轨迹，可以近似描述钻孔的实际轨迹，实践中通常用实测轨迹表示实际轨迹[8]。绘制实测轨迹时，需建立坐标系用于描述钻孔轨迹，然后测量钻进中钻杆的姿态参数，最后通过相关算法处理数据并绘制轨迹。

1.1 钻孔轨迹空间坐标系

在煤矿钻井中，对钻进轨迹进行描述和绘制，实质是描绘其在地理坐标系(n系)中的位置。同时，将载具在运动中的变化视作刚体的旋转，建立载具坐标系(b系)描述旋转。

地理坐标系以当地的地磁北为北(N)，在水平面上与N轴向右垂直为东(E)。取水平面向上的方向为正方向(D)，零点(O)一般选在钻机所在的位置，或者开孔点的位置。建立的地理坐标系如图1所示。

图1 钻孔轨迹坐标系

钻具坐标系原点取在钻具的质心，以钻进方向为横方向x轴，y轴沿钻具的纵方向，z轴垂直于钻具平面向上，如图1所示。x′为钻具坐标系的x轴在水平面上的投影。

1.2 钻孔轨迹的基本要素

角度要素：ψ为方位角，是钻具坐标系x轴在地理坐标系水平面上的投影与地理北轴的夹角；θ为倾角，是钻具坐标系x轴与水平面的夹角。

钻孔深度L为沿着钻孔轨迹轴线到测点的曲线长度，通常用钻杆总长度近似。在实际生产中，通常选择1根或2根钻杆的长度作为测距ΔL，即每钻进1根或2根钻杆，在加杆时获取姿态角，进行轨迹计算与绘制。

1.3 方向余弦阵

(1)

(2)

该矩阵的求解，采用四元数法。因为欧拉角法在倾角接近90°时存在奇点，会导致算法失效；方向余弦法需要求解9个一阶方程来，比较复杂；四元数法可以简单地描述旋转运动，且计算量较小，故采用四元数法进行求解[9]。

2 基于四元数法的惯性导航测量原理

2.1 惯性导航姿态测量

钻孔轨迹绘制需要得到轨迹基本要素中的姿态角。姿态角的测量方法采用加速度计和陀螺仪组合测量，加速度计测量加速度值，陀螺仪输出转动角速率。采用四元数法解算姿态角，其原理框图如图2所示。

图2 姿态角测量原理

2.2 机械陀螺仪原理

陀螺仪又被称为角速度传感器。机械陀螺仪内部质量块在激励力的作用下向某一轴产生振动，当质量块绕其中心轴旋转时，在与振动轴、角速度输入轴正交的另一方向将存在科氏力[10]。在载体上正交安装3只机械陀螺仪，通过检测陀螺仪质量块的科氏力的大小和方向，在固定振动速度的情况下可计算出物体的旋转速度ω。

单个陀螺仪在使用中存在漂移的问题，引入加速度计可以一定程度上矫正陀螺仪的漂移。

2.3 加速度计原理

加速度计测量的量为比力，是物体受到的万有引力与其他力作用的结果。如图3所示，由于重力始终朝下，根据3个轴检测的重力分量。倾角的解算式如式(3)所示。解算出初始值，也可作为陀螺仪的矫正值

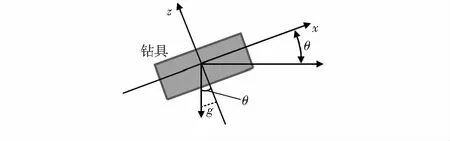
图3 加速度计测量倾角示意

(3)

式中gz为重力在z轴的分量，gx为重力在x轴的分量，gy为重力在y轴的分量。

2.4 四元数解算姿态角

从载具坐标系到地理坐标系的变换，可以看作是某一矢量从载具坐标系rb旋转到地理坐标系rn，旋转四元数为q，其旋转用四元数表示为

q=p0+p1i+p2j+p3k

(4)

rn=q⊗rb⊗q-1

(5)

(6)

2.5 微惯性组合单元MPU6050

MPU6050包含了惯性导航单元以及温度传感器，具有体积小、价格低廉、精度好、读取速度快、能耗低等优点，其工作温度为-40～85 ℃，优于一般FOG，更适应煤矿下的工作环境温度。 MPU6050自带的DMP模块通过调用函数对获取的数据进行四元数求解，即可得到所需姿态角。由于加速度计在运动时误差较大,静止时误差较小，陀螺仪恰好相反，运动时姿态角求解将增大陀螺仪数据的权重，静止时增加加速度计的权重。

3 钻孔轨迹绘制与误差分析

3.1 钻孔轨迹

工程上通常使用二维相对坐标系进行轨迹绘制。以初始钻进方向为基准线，进行相对偏差计算，在竖直平面和水平面绘制，可以更直观地反映钻进轨迹偏离设计轨迹的情况。方位角初始值需外部测量，实际方位角与测量方位角的偏差值为α，初始值设定为0。

3.2 平均角法计算坐标

在随钻测量中，采用递推累加的方式计算下一测点的位置。设定开孔的位置为坐标原点(0,0,0)，测得下一测点的姿态角，测距ΔL在地理坐标系各个轴的分量值即是下一点的坐标增量，连接各增量值即可绘制轨迹图。

本文选择平均角法进行轨迹坐标的计算。假设钻进中相邻两测点之间为直线段，长度等于测距ΔL，且直线的倾角和方位角分别等于上下两测点倾角和方位角的平均值[12]。将测距ΔL投影到水平与竖直平面，得到轨迹计算示意图如图4所示。

图4 平均角法轨迹计算坐标

根据坐标图可得到坐标增量的计算如式(7)所示

(7)

三维空间坐标值计算如式(8)所示

(8)

3.3 实验测量与轨迹绘制

实验模拟打钻工艺，每加装一根钻杆测量一次，每次钻进长度设定为1 m。初始方位角为232°，初始方位角的偏角为0，倾角为3.64°。读取钻进过程中的方位角与倾角信息的频率设为10 Hz，通过平均角法进行轨迹坐标计算，用MATLAB绘制轨迹三维视图如图5所示。

图5 钻孔轨迹三维视图

由图5可以看出，由测量数据计算得到的轨迹，在前半段与实际轨迹近乎重合，在后半段与实际轨迹之间出现了较大偏差，说明存在累计误差。

通过观察图6所示的二维投影图可以发现，测量轨迹在竖直平面上的投影与实际轨迹几乎重合，水平投影出现了一定的偏差。说明通过MPU6050获取的倾角准确度很高，因为加速度计对倾角测量值进行了修正，而方位角则出现了一定的偏移，需要对陀螺仪的误差进行分析。

图6 钻孔轨迹二维投影

3.4 误差分析

出现上述误差的原因可以从设计理论缺陷和硬件误差两个角度出发进行分析。

理论缺陷：采用加速度计作为倾角的初始值与矫正值时，测量的各轴向所受加速度或者说比力的大小，对测量值求解反三角函数即可得到倾角与工具面角的大小，如式(3)、式(4)所示。而对方位角的求解是将陀螺仪的测量值进行积分得到的，若测量时出现误差，将会通过积分放大，加之测量轨迹时采用累加法，导致误差会在求解过程中累积，形成累计误差。上述误差可通过缩短测距减小。

陀螺仪本身存在误差[13]：陀螺仪的误差主要由温度、有规律漂移量与随机偏移量决定。不同温度下的偏移有所不同，温度发生变化对实验结果影响较大。随机漂移是指陀螺仪启动时产生大小方向不固定的偏移。MPU6050的DMP模块启动时间为8 s，在这8 s中测量值会朝着某一方向变化，直至稳定下来，稳定后的值为随机漂移量。有规律的偏移为陀螺仪参数大小遵循一定规律的漂移。在温度为24 ℃时MPU6050的方位角偏移为每分钟0.3°。

实验时,为了使精度提高，去除随机漂移量，按规律减去有规律的偏移，再保持测量温度在固定条件下，就能使得实际测量值更接近真实值。经修正后的轨迹如图7所示，测量轨迹与实际轨迹更接近，测量结果满足工程上的精度要求。