基于RBF神经网络的地铁隧道施工坍塌事故应急车辆需求预测

邓林，陈玉斌，刘湘慧，陈赟

(1. 湖南交通职业技术学院 建筑工程学院，湖南 长沙 410132；2. 长沙理工大学 交通运输工程学院，湖南 长沙 410114；3. 中铁建港航局集团勘察设计院有限公司，广东 广州 511442)

近年来，随着城市化进程的不断加快，地铁成为城市轨道交通网络建设的重要内容。但其建设过程具有较大的不确定性和风险，从而导致地铁隧道施工坍塌事故时有发生。为减少人员伤害和财产损失，事故发生后及时、合理的应急救援尤为重要，其中应急资源类型和规模的选择是实施救援的前提和基础。为提高救援效率，保证应急资源的合理调配和利用，已有学者指出消防部队、医护人员、工程器械和药品等[1-2]是应急资源的重要组成部分，且应急车辆是应急资源的核心[3]。目前，对于应急资源调配和利用的相关研究主要集中于应急资源调度和应急资源预测两方面。在应急资源调度方面，主要包括运输路径选择及资源配置优化[4-7]等相关研究。在应急资源预测方面，学者们将多米诺效应、蒙特卡洛、鲁棒优化模型、直觉模糊集和案例推理等方法[8-10]引入其需求量的预测过程中。现有研究主要集中于突发事件应急资源总体上的预测和调度，缺少对地铁隧道施工过程中具体突发事件以及特定性的应急资源的相关研究。而在地铁施工坍塌事故中，展开对于医疗救护力量和消防救援力量需求的预测具有一定的现实意义。此外，在现今大数据时代，神经网络技术在应急管理领域得到了较为全面的应用，如应急资源需求预测、应急能力评价和应急疏散仿真等，其适用性和合理性已经得到了验证。在模拟预测方面，相较于传统统计回归模型，神经网络模拟预测能力更强，对样本数据不要求其具有很强的规律性，且相对误差较小，地铁隧道坍塌事故突发性质决定了样本数据的不规律性[11]。因此，可以将神经网络技术引入地铁隧道施工坍塌事故的应急资源需求预测中。综上所述，本文从应急车辆需求量预测角度出发，结合行业标准及相关规定，以救护车和消防车数量为预测目标，考虑神经网络技术的优越性，利用RBF 神经网络技术，构建地铁隧道施工坍塌事故应急车辆需求量预测模型，对应急车辆及其关联的应急人员数量展开预测，提供调度建议，为事故应急决策提供参考。

1 地铁隧道施工坍塌事故应急车辆需求预测输入指标确定

为明确地铁隧道施工坍塌事故应急预测输入指标，本文借鉴其他领域在应急资源需求量预测输入指标选取方面的研究[12-14]，归纳得到各类输入指标的选取应主要考虑以下3个类型。

1) 反映救援基本需求。承受灾害事故不利影响的人或物的数量或规模，如受灾人数、房屋倒塌规模。

2) 反映救援难度。事故灾害的自身信息，如台风灾害的风速、地震灾害的震级、洪涝灾害的洪水等级等。

3) 反映事故影响范围。事故灾难受损范围的基础信息，如灾区规模、电网规模等。

地铁隧道施工坍塌事故隶属于生产安全事故，造成的事故影响包括人员伤害、周边建筑物塌陷和路面交通受损等，与其他类型的事故灾难在损害结果和救援目标上相似。因此，本文从以上3类指标出发，结合所确定的应急资源类型——救护车及消防车选取预测输入指标，选取依据如下：

1) 与救护车数量和消防车数量的需求量判断相关联。

2) 可以反映承受事故不利影响的人或物的数量和规模、事故灾难的自身信息和项目基本信息。

3) 可以迅速采集即时信息或存在预留信息，保证应急资源需求量预测的时效性。

4) 可以对指标直接进行量化，或通过预处理后进行量化，便于直观构建预测模型。

5) 可以获取完备的训练数据以进行预测模型的训练。

综上所述，最终确定坍塌位置(c1)、次(衍)生事故(c2)、坍塌面积(c3)和被困人数(c4)作为地铁隧道施工坍塌事故应急车辆的预测输入指标，各指标含义如表1所示。

表1 地铁隧道施工坍塌事故应急车辆需求量预测输入指标Table 1 Prediction input index of emergency vehicle demand for subway tunnel construction collapse accident

2 地铁隧道施工坍塌事故应急车辆需求预测模型构建

RBF(Radial Basis Function)神经网络又称径向基函数神经网络，是一种3层前向神经网络，具有结构简单、计算量少、收敛速度快和无局部最优等特性[15]。其基本原理是通过径向基函数，对输入的低维数据进行非线性变换，形成高维隐含层，隐含层再通过线性变换输出数据。

本文构建的地铁隧道施工坍塌事故应急车辆需求预测模型输入层由坍塌位置(c1)、次(衍)生事故(c2)、坍塌面积(c3)和被困人数(c4)4 个节点组成。同时，为提高预测准确性，将救护车数量(d1)及消防车数量(d2)2 个变量分别作为输出层节点，构建2个RBF 神经网络。通过案例搜集基础数据，量化指标作为训练样本，以及网络结构训练预测模型，在误差允许范围内测算结果。

2.1 数据处理

2.1.1 数据量化方式及取值范围

搜集地铁隧道施工坍塌案例共61 例，其中由于自然条件引发的事故和施工过程中人为失误的事故12 例，事故发生所在地偏远的事故13 例，被划分为重大事故的事故10 例。案例数据整理和分析过程中，剔除缺失和数据偏离均值较大的数据组，保留有完整输入指标的数据共47组。

结合以上事故案例，对坍塌位置(c1)、次(衍)生事故(c2)、坍塌面积(c3)和被困人数(c4)的量化方式及取值范围进行选择。对指标c1，地铁隧道施工坍塌位置分为洞口、洞身和其他位置(机械内部和其他掩埋物内部)。洞口坍塌较洞身坍塌和其他位置坍塌可供救援设备安置和救援人员操作的开放空间较大，救援难度较小；洞身坍塌事故多伴随路面塌陷或建筑物沉降，救援难度居中；其他位置坍塌是在隧道本身坍塌的基础上伴随着其他结构物、机械设备或施工材料的继发坍塌，救援难度大。综上，洞口、洞身和其他位置的救援难度是递增的，分别赋值1，2 和3。对指标c2，无次(衍)生事故和有次(衍)生事故的救援难度是递增的，分别赋值0 和1。对指标c3和c4，为数值型指标，可根据事故情况取值，各指标量化方式及取值范围见表2。

表2 指标量化方式及取值范围Table 2 Ⅰndex quantification method and value range

2.1.2 数据预处理

通过对61 例案例数据的整理和分析，剔除数据缺失和数据偏离均值较大的数据组，保留有完备输入指标和输入指标的数据组共47 组。各数据组有c1，c2，c3，c4，d1和d2共6 项数据，记为样本矩阵X47×6。

为消除各变量量纲不同对预测结果的影响，需要对数据进行归一化处理。对于第i个样本的第j个数据xij，其归一化数据x*

ij计算公式如下：

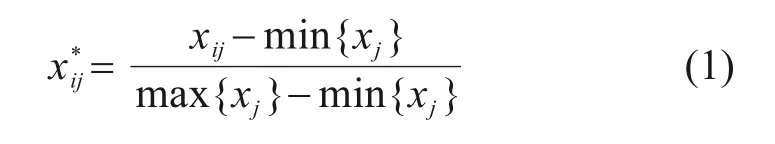
其中：min{xj}和max{xj}分别为第j列数据的最小值和最大值。

2.2 代码实现与结果分析

本文选用Windows10 环境下MATLAB R2018a软件进行模型构建和训练，基于47 组样本数据随机生成37 组训练集和10 组测试集样本。选用matlab 中的newrb 函数构建神经网络，该函数通过不断增加隐含层神经元个数直至满足目标误差为止，可以较好地解决隐含层难以确定的问题。样本归一化数据精度为0.001，因此设定目标误差为0.001，最大神经元个数为100，每次返回增加神经元个数为1。为防止过拟合，分别选取扩展速度spread为0.01，0.05，0.1，0.5，1和3进行训练。

以救护车数量RBF 神经网络预测模型为例，不同的扩展速度训练结果如表3所示。

结合训练结果和表3 的对比分析结果可知，spread 取0.01 和0.05 时，救护车数量训练数据和预测数据基本重合，形成了过拟合；spread 取3 时，救护车数量训练数据和预测数据偏差较大。综合对比隐含层神经元个数和均方误差，选取spread值为0.1，救护车数量预测模型训练结果如表4和图1所示。

表3 扩展速度对比表Table 3 Expansion speed comparison table

表4 救护车数量newrb函数训练结果Table 4 Number of ambulances newrb function training result

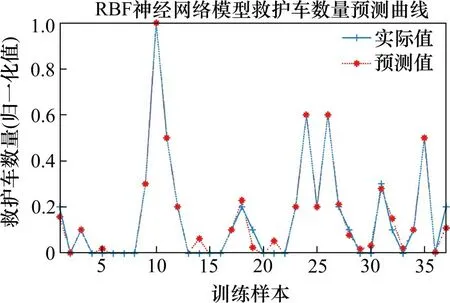
图1 救护车数量训练集样本数据对比Fig.1 Comparison of sample data of ambulance number training set

由表4 可知，隐含层神经元个数为15 时，其均方误差MSE 可以满足目标误差要求。由图1 可知，该预测模型对于救护车数量能够较好地拟合训练集历史数据，误差较小(＜0.001)。将测试集代入计算，并将预测数据与实际值进行对比可得图2。

由图2可知，该预测模型对于救护车数量测试集样本预测准确率为90%(反归一化后取整数据的准确率)，相关系数R2=0.965 21，进一步验证了模型的可靠性。

图2 救护车数量测试集样本数据对比Fig.2 Comparison of sample data of ambulance number test set

同理，对消防车数量RBF 神经网络预测模型进行训练，选取spread 值为0.1，消防车数量预测模型训练结果如表5和图3所示。

表5 消防车数量newrb函数训练结果Table 5 Number of fire engines newrb function training result

由表5 可知，隐含层神经元个数为21 时，其均方误差MSE 可以满足目标误差要求。由图3 可知，该预测模型对于消防车数量能够较好地拟合训练集历史数据，误差较小(＜0.001)。将测试集代入计算，并将预测数据与实际值进行对比可得图4。

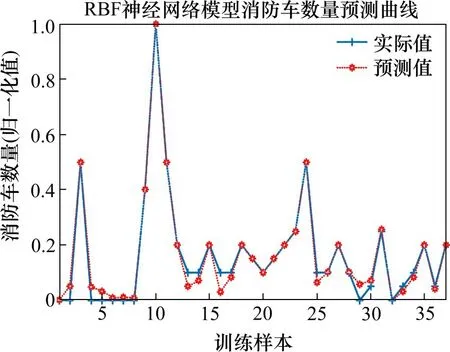
图3 消防车数量训练集样本数据对比Fig.3 Comparison of sample data of training set for the number of fire engines

由图4可知，该预测模型对于消防车数量测试集样本预测准确率为80%(反归一化后取整数据的准确率)，相关系数R2=0.958 35，进一步验证了模型的可靠性。

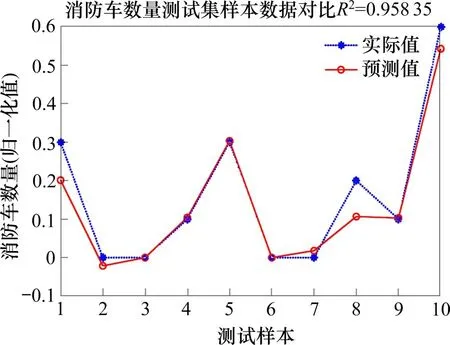
图4 消防车数量测试集样本数据对比Fig.4 Comparison of sample data of test set for the number of fire engines

3 地铁隧道施工坍塌事故应急车辆需求量预测与实施建议

3.1 地铁隧道施工坍塌事故应急车辆需求量预测

3.1.1 项目描述

2016年10月19 日上午8 时45 分左右，某地铁区间正线左线隧道发生坍塌事故，事故造成现场作业人员3 人死亡，直接经济损失约450 万元。该合同段采用暗挖法和明挖法结合施工，事故段采用台阶法施工。

该事故发生的直接原因包括：1) 坍塌处的地质条件复杂，地层变化大。2) 事发点地处十字路口，重载车往返频繁，震动及动载对下部隧道内施工空顶期土体稳定性造成不利影响。3) 事故掌子面处上方土体塌方后，局部土体流动和应力释放迅速波及后方上台阶初支结构，进而导致初支全封闭和未全封闭处上部结构发生断裂。

该事故发生的间接原因包括：1) 施工单位对总体风险预判不足，监测不到位，未采取有效的安全保护措施；对作业人员的安全教育不详实。2)监理单位对监测工作未进行有效地指导和监督，对事故隐患未提出防范措施和建议。3) 建设单位对施工扰动预估不足，对作业人员的安全教育指导不力。

3.1.2 应急车辆预测

据调查显示，该地铁隧道施工坍塌发生在洞身处，未引起其他次(衍)生事故，坍塌面积为50 m2，造成3 人被困。据此，该项目预测指标取值如表6所示。

表6 事故案例预测指标取值Table 6 Value of accident case prediction index

通过代入训练后救护车数量RBF 神经网络预测模型和消防车数量RBF 神经网络预测模型进行计算。通过归一化、计算预测值、反归一化和取整数等步骤，最终计算得该突发事件的救护车需求量为3辆，消防车需求量为5辆。

3.2 应急车辆调配对策分析与验证

事故案例在事故调查或新闻媒体报道中均未体现应急资源的准确数量，但考虑目标情景的被困人员数量和坍塌规模，并查阅事故现场附近的医疗机构和消防机构距离等信息，可以认为预测值已经能够基本满足救援需求。

基于前述应急资源需求量预测模型，可以对救护车和消防车的需求量进行预测，实际资源调配对策应在二者的基础上进一步推算医护人员数量和消防车人员数量。由于事故的特殊性和事故间的差异性，还需要对预测结果进行修正。

1) 根据卫生行业标准《救护车(WS/T 209—2008)》，一辆A 型救护车或B 型救护车应配备司机1名，医生1名，护士1名，担架员2名，以及必要的医护设施，至少可容纳1 名随行家属和1 名伤员。

2)根据国家通用技术标准《消防车第1 部分：通用技术条件(GB 7956.1-2014)》，灭火消防车、举高消防车和专勤消防车应配备5～7 人消防救援人员，本文取6人/辆。

3) 应急资源调配对策反映的是应急资源需求量的最低限值。由于预测模型的预测值是归一化后的精确值，反归一化后数据小数位易被忽略，为满足应急资源的最低限值需要，决策者应对其最终取值逢小数位进一处理，保证救援的基本需求。

4) 对于预测结果显著不合理的地方，则需要按照一般应急处置经验对资源调配对策进行修正。还应考虑应急储备、项目所在地周边医疗机构与消防机构自身的救援能力、救援设备的周转能力等，进而对应急资源调配对策进行修正以满足实践需求。

综上，该事故案例应在事故爆发后委派至少3辆A型救护车或B型救护车，每辆救护车应配备司机1 名，医生1 名，护士1 名，担架员2 名，以及必要的医护设施，每辆至少可容纳1名随行家属和1 名伤员。同时，需要委派至少5 辆灭火消防车、举高消防车或专勤消防车，每辆消防车应配备6名消防救援人员。

4 结论

1) 通过归纳文献资料的输入层指标，结合历史事故数据结构和应急需求，确定了将坍塌位置、次(衍)生事故、坍塌面积和被困人数作为输入层指标。

2) 构建了救护车数量RBF 神经网络预测模型和消防车数量RBF神经网络预测模型，2个预测模型在训练集拟合程度较好，测试集的样本准确率分别为90%和80%，验证了模型的可靠性。在应急资源调配对策选取和修正中，应结合相关规范和实践需求，对应急资源调配对策进行进一步的选取和修正。

3) 本文构建的应急车辆预测模型均基于搜集的案例数据，在数量上和信息维度上都存在一定的局限性，在实践中需要不断更新案例，不断更新预测模型，以提高方法的准确性。