基于时间序列分析和信息熵的结构损伤识别

董家凡，潘玉恒，鲁维佳

(天津城建大学 计算机与信息工程学院，天津 300384)

随着工程技术的进步，桥梁的类型和结构形式日益复杂，人们对桥梁的安全性越来越重视。由于桥梁的设计使用年限较长，在长期的使用过程中会产生一系列的老化和损伤，因此从安全角度出发，监测桥梁结构的运行状态并准确识别结构随时间发生损坏的位置和严重程度是一项非常重要的工作。结构的损伤识别方法可分为两大类：模态参数法和非模态参数法[1]。模态参数法通过检测由损伤引起的模态参数的变化来确定损伤程度，如频率[2-3]、模态形状[4-5]、曲率模态[6-7]、柔度[8-9]和模态应变能[10-11]等，基于模态参数的损伤识别方法易受环境噪声、温度和交通状况的影响，这些外界因素以非线性的方式影响桥梁刚度，进而改变桥梁的模态特性，最终导致错误的检测结果[12]。非模态参数法因其无需构建精确的有限元模型，且具有较强的抗噪能力，被广泛应用于监测结构损伤前后测量数据的变化。时间序列模型法作为非模态参数法的一种，因其能够校准结构的动态响应并能快速识别异常数据而被广泛应用于结构损伤识别中。张玉建等[13]针对现有损伤识别方法提出了基于具有外部输入的自回归模型，实现了损伤结构的定位和定量分析。GHAREHBAGHⅠ等[14]利用自回归时间序列模型的系数和残差，提出一种称为最佳不相关特征选择算法提取损伤特征，用于检测结构的损伤。为解决实际工程应用中结构的非线性损伤问题，CHEN 等[15]通过将非线性广义自回归条件异方差(GARCH)模型应用于框架结构中，有效地识别了结构的损伤。周建庭等[16]提出了融合kalman滤波和GARCH模型的结构损伤识别方法，利用非线性递归模型实现对损伤结构的精确识别，有效地降低了识别误差。虽然时间序列模型法在结构损伤识别领域取得了一些研究成果，能精确定位损伤，但是仅利用时间序列模型中的统计指标难以建立与损伤程度之间的关系，无法实现损伤程度的量化。基于此，ZHANG 等[17]利用正则化ARMA 模型拟合虚拟脉冲响应，将模型系数的一范数作为损伤敏感特征指标，但所提取的模型阶数过大，对损伤程度的度量结果不明显。NAⅠR 等[18]研究发现前三阶AR 系数的平方和和平方根归一化的第一个AR 系数提供了对结构损伤最鲁棒的敏感特征。LE 等[19]提出了基于ARⅠMA 模型和马氏距离的特征提取算法，该方法可以识别不同程度的损伤，但未能精确量化损伤。ZHU 等[20]利用稀疏正则化求解AR 模型系数，并构建自回归系数与刚度折减系数之间的灵敏度矩阵，实现了损伤位置和损伤程度的判定，但该方法增大了运算量，不利于实时监测结构健康状况。本文结合ARMA 模型系数在结构损伤识别方面的优势，提出了一种新的损伤指标用于结构的损伤检测，实现损伤的定位和量化分析。本方法从理论上推导了自回归系数与结构振动频率之间的关系，引入信息熵实现对节点信息的量化度量，利用结构损伤前后ARMA 模型系数的变化检测损伤，所提出的损伤指标能够同时判定损伤结构的位置和损伤程度。并以常见的简支梁结构及ASCE美国结构健康监测小组的ⅠASC-ASCE 基准结构[21]为例，对方法的有效性进行验证。

1 理论方法

时间序列模型可以将大量结构响应数据所蕴含的信息凝聚为少数模型参数(自回归系数、滑动平均系数和模型残差方差)[22]，解决了结构损伤检测过程中因测量的数据较多无法直接评估结构的健康状况的问题。本文对测量的加速度时程数据建立ARMA 模型，分析自回归模型系数与振动频率的关系，建立损伤程度与模型参数之间的依据，引入信息熵实现对节点信息变化量的度量，利用结构损伤前后ARMA 模型系数信息熵的变化检测损伤位置和量化损伤程度。

建模之前，对测量到的振动数据进行标准化处理，消除其他荷载条件的影响。将每个传感器记录的加速度时间序列进行以下的归一化：

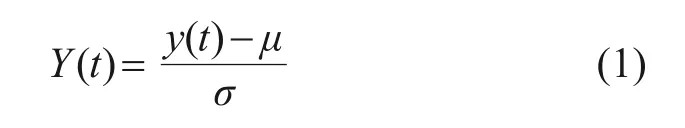
式中：Y(t)表示对时间序列y(t)标准化之后的结果，μ为y(t)的均值，σ为y(t)的标准差。然后，对标准化序列Y(t)建立ARMA模型进行分析，模型如下：

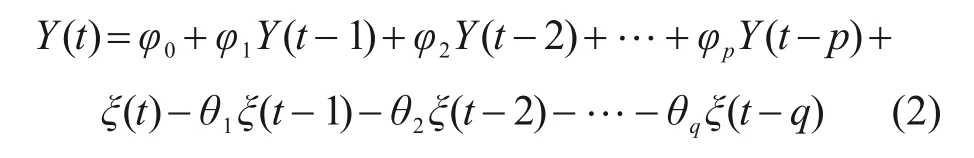
式中：φ0是模型的常数项；φ1,φ2,…φp是自回归模型AR(p)的系数；θ1,θ2,…θq是移动平均模型MA(q) 的 系 数；ξ(t),ξ(t-1),…,ξ(t-q) 是 时 间t,t-1,…,t-q的随机误差。ARMA 模型的系数由极大似然估计法确定。

自回归系数包含了关于模型固有频率和阻尼比的信息，在线性输入振动背景下，ARMA 模型可被看作是具有外部输入时间序列的自回归模型。应用z变换的时移特性，可以在复z域中检验该模型。将公式(2)两边同时求z变换：

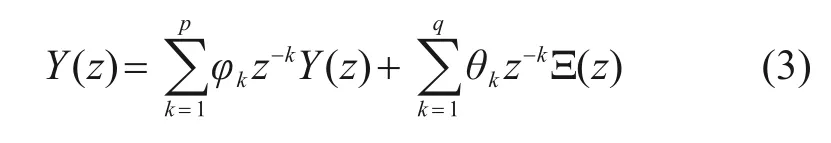
式中：Y(z)和Ξ(z)分别是Y(t)和ξ(t)的z变换。传递函数H(z)为：

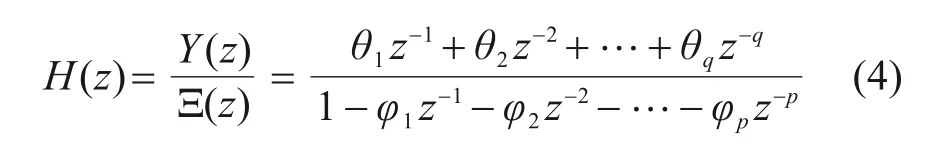
传递函数的分母Ξ(z)是一个p阶多项式，称为特征方程：

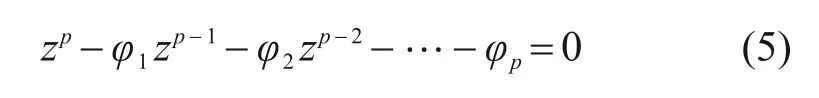
特征方程共有p个根，将其因式分解为：

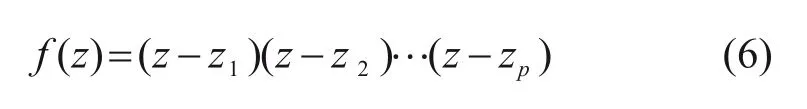
根据韦达定理，得到以下特征方程的根与ARMA模型系数之间的关系：

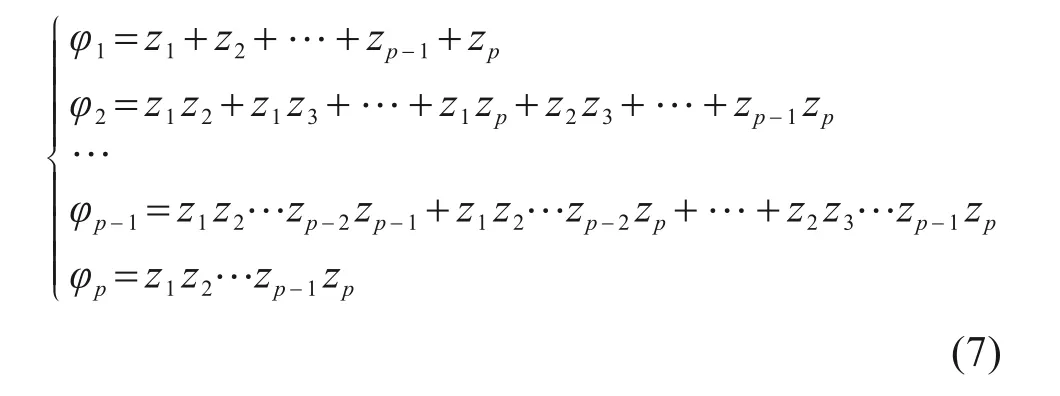
公式(7)中z1,z2,…,zp为系统特征方程的根，φ1,φ2,…,φp为ARMA模型的系数。

系统特征方程的根与固有频率和阻尼比之间的关系为：

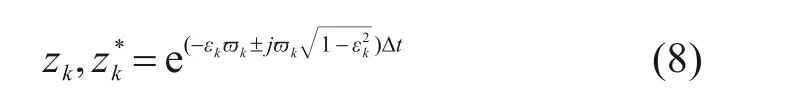
式中：ϖk和εk分别为k阶模态的固有频率和阻尼比，为系统特征方程的一对共轭根，k=1,2,…,p/2，Δt为采样的时间间隔。

不同损伤情况下的ARMA 模型系数的不同可以表示为固有频率和阻尼比的改变。参考文献[18]中也指出，刚度因损伤的发生而降低时，结构的响应将会发生变化，从而导致自回归系数的改变。对于一个高阶模型，韦达定理无法直接求解系统的固有频率和阻尼比，本文基于此研究理论，引入信息熵实现对节点信息变化量的度量，提出了一种基于信息熵的损伤指标，量化固有频率和阻尼比的变化，检测结构发生损伤的位置和损伤程度。

信息熵是由香农在1948年提出的，实现了对信息的量化。信息熵定义如下：式中：S是系统信息熵，pi表示的是事件i在所有事件记录中的概率。例如，在本研究中pi为第i阶自回归系数占全阶系数和的比重。pi表示如下：

定义结构损伤指标为ARMAPE，其中Su和Sd为损伤前后模型系数的信息熵值

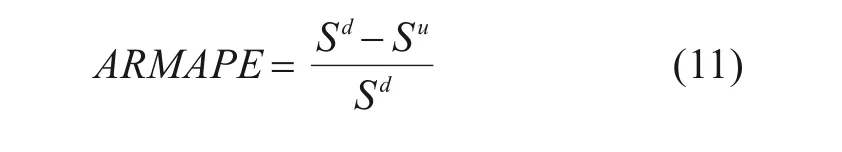
2 数值仿真：ⅠASC-ASCE基准结构

为了验证理论方法的有效性，将所提出的损伤识别方法应用在ASCE健康监测小组提出的基准结构上。该基准结构是一个4 层2 跨2 跨钢框架比例模型，如图1所示。传感器的放置位置按照方向的不同分别编号为X和Y，在仿真过程中，通过拆除结构中的支撑来模拟损坏，测试案例1中拆除第1层的所有支架，测试案例2拆除第1层和第3层的所有支架，测试案例3 拆除第1 层的一个支架，测试案例4 分别拆除第1 层和第3 层的一个支架，损坏模式由图2中虚线画出的支撑表示，对损伤前后的模型框架进行振动测试，记录加速度传感器的时程数据，实验采样频率设置为1 MHz，加速度时间历程为40 s，图3(a)表示测试案例1 中传感器1Y测量的损伤前后加速度时程曲线，为了能清楚地看出在损伤前后加速度时程曲线的差异，在图3(b)中将图3(a)中第10 s 至第15 s 内的时程曲线进行了放大。各案例的刚度折减系数如表1所示。

表1 实验工况Table 1 Experiment case

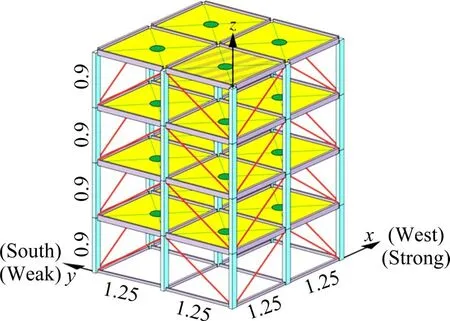
图1 模型结构Fig.1 Model structure

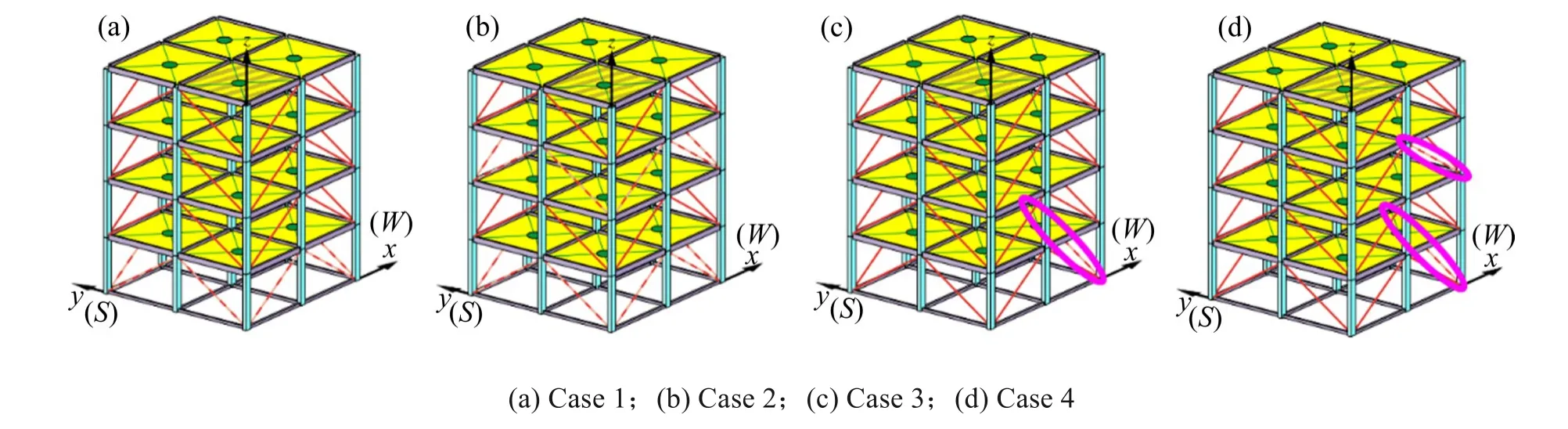
图2 损坏模型Fig.2 Damage model

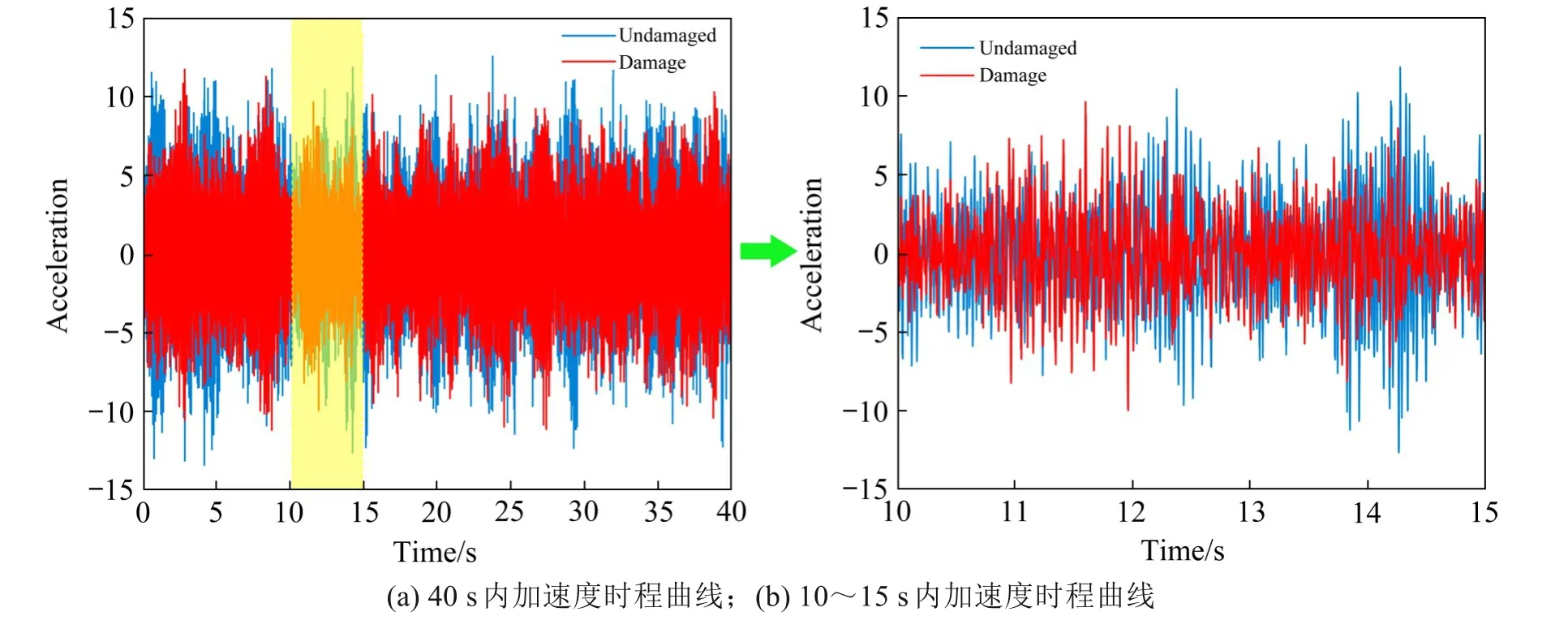
图3 加速度时程曲线Fig.3 Acceleration time curves

图4 显示了基准结构的损伤识别结果。1X 表示框架第1 层西面放置的传感器编号，1Y 表示框架第1 层北面放置的传感器编号。图4(a)，4(b)中1X 和1Y 的ARMAPE 值明显较大，能准确定位结构的损伤位置。图4(c)中为单一支架损伤识别结果图，其中测得的ARMAPE 值为0.178，与理论值0.17 的误差仅为0.047。图4(d)中分别拆除第一层和第3 层的一个支架，经计算得到的ARMAPE 值分别为0.178 和0.120，最大误差为0.09。根据实验结果图4(a)，4(b)可知，Case 1 和Case 2 中每层破坏的支架数较多，仅凭借单一传感器测量值进行损伤检测会存在误差，识别的损伤程度与理论值存在差异，但从整体的识别效果可知，所提出的基于时间序列模型的损伤识别方法可以检测、定位和量化结构中的损伤。

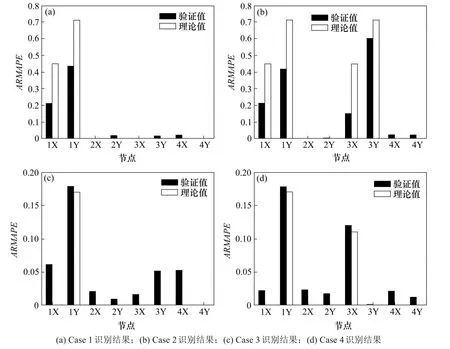
图4 损伤识别结果Fig.4 Damage identification result

3 实验案例：组合梁结构

为了更进一步验证本方法的可行性，实验设计了一个6 m 长，0.9 m 宽的钢-混凝土组合桥梁模型，模型横截面尺寸为900 mm×90 mm，18 个节点，每个节点处纵向安装4 个剪力连接件。将11个加速度传感器均匀布置在模型表面，模型内嵌有18 组可拆卸的剪力连接件，所有剪力连接件通过力矩扳手紧固到120 N·m 的扭矩。混凝土面板和钢梁为紧密连接状态，将梁板分开浇筑，每个剪力连接件由梁拱腹的螺纹杆组成，并系在嵌入的螺母帽中，桥梁模型支座宽度为0.5 m，高度为0.8 m，设计的桥梁模型如图5所示。

图5 组合梁模型Fig.5 Composite beam model

实验使用NⅠ加速度传感器，相比于桥梁的质量传感器自重可以忽略，不影响组合梁桥的自振频率。利用磁性支座将加速度传感器固定在钢梁上，如图6 所示。利用COⅠNV 北京东方振动和噪声技术研究所的ⅠNV306U 型号动态采集仪进行数据采集，该采集仪最高采样频率为1 MHz，将动态采集仪主机与显示器连接，并将信号显示输出。为了模拟真实桥梁结构的损伤情况，实验设置单一损伤和多重损伤2种模式，并通过拆除不同数量的连接件，引入不同程度的损伤，使用锤击法测试损伤前后各种工况下的振动加速度，实验装置如图7 所示。采样频率设置为1 MHz，加速度时间历程为20 s，实验损伤工况如表2所示。

图6 传感器位置Fig.6 Sensors location

图7 实验装置Fig.7 Experimental device

表2 损伤工况Table 2 Damage case

考虑到损伤是由拆除剪力连接件产生的，结构的损伤程度由损伤前后钢-混凝土组合桥梁的极限抗弯强度折减系数表示。实验中假设健康状况下钢-混凝土板为完全交互作用，采用完全剪力连接。考虑到桥梁跨度问题，在进行损伤实验时，以节点A6 为中心将组合梁分2 部分进行损伤的定位和定量分析。剪跨中连接件个数与钢-混凝土组合桥梁极限抗弯强度之间的关系[23]：

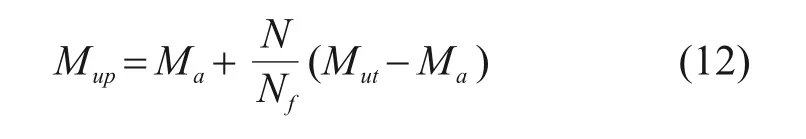
式中：Mup为拆除部分栓钉情况下组合梁的极限抗弯强度，Ma为纯钢梁的塑性抗弯强度，N为组合梁中的实际栓钉个数，Nf为完全剪力连接时组合梁中栓钉个数，Muf为完全剪力连接时组合梁的极限抗弯强度。

损伤前后强度折减系数为α，和分别为损伤前后组合梁的极限抗弯强度。

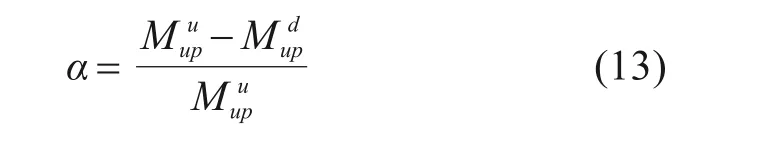
图8(a)和8(b)显示了2 种单一损伤状态下损伤识别结果。在图8(a)中，节点3处的ARMAPE值明显低于其他未受损节点，这一结果与实验工况OM1 的损伤节点位置一致。识别的ARMAPE 值为0.115，实验验证值与理论损伤严重程度值0.111 的误差仅为0.036。在图8(b)中，节点8 处识别的ARMAPE 值为0.278，其他未损坏节点处的识别值接近于0，与理论值一致。实验结果表明，在单一损伤工况下，损伤节点的位置可以被准确定位，并且识别的损伤严重程度接近理论值。

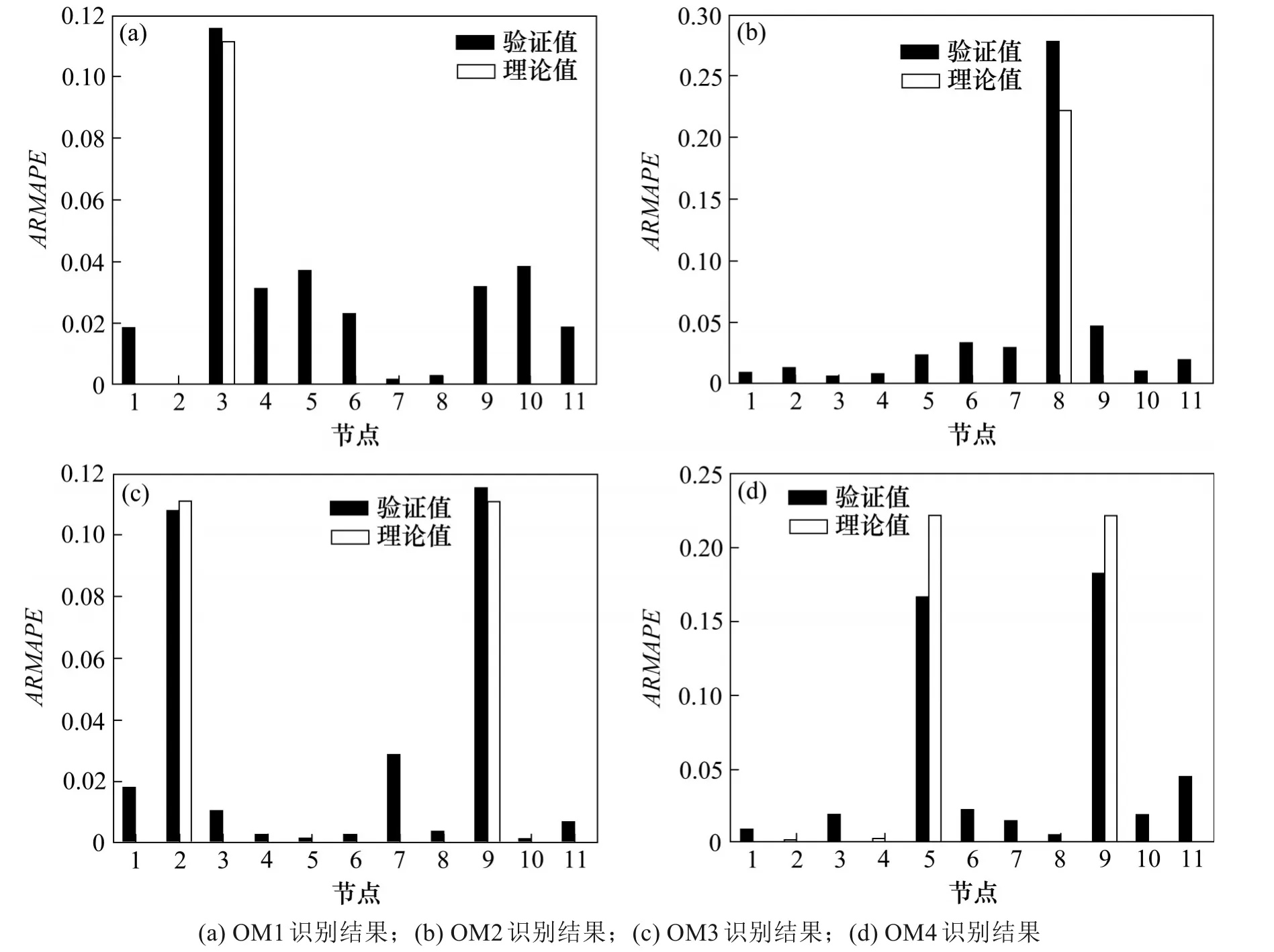
图8 损伤识别结果Fig.8 Damage identification result

图8 (c)，8(d)显示了多重损伤状态下的损伤识别结果。图8(c)显示了在节点2 和节点9 处ARMAPE 值明显增大，识别结果与实验设置的损伤位置相同，且节点2和节点9处的ARMAPE值分别为0.108 和0.116，与理论值的最大误差仅为0.045。图8(d)中节点5 与节点9 处的ARMAPE 值分别为0.167和0.183，明显大于其他无损节点。实验结果表明，多重损伤情况下的损伤节点位置能够被准确定位，识别的损伤严重程度与理论损伤严重程度一致。

4 结论

1) 从理论上推导了ARMA 模型的自回归系数与结构损伤的关系，将模型系数作为损伤敏感特征，通过提取结构受损前后的自回归系数并结合信息熵理论，提出ARMAPE 指标，实现对损伤结构的定位和损伤程度的量化分析。

2)通过在实验室的钢-混凝土简支梁和ASCE健康监测小组提出的一个基准结构上的应用，本文提出的方法对单一损伤和多重损伤均可进行损伤定位，并在损伤定位的同时实现损伤程度的量化。