考虑桥墩撞击的整体式刚构桥列车走行性分析
2022-08-29戴公连肖尧郭向荣葛浩
戴公连,肖尧,郭向荣,葛浩
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 长江勘测规划设计研究有限责任公司,湖北 武汉 430010)
整体式桥梁采用墩梁固结的构造,全联无支座,既保留了连续梁无伸缩缝、线路平顺的优点,又兼有便于施工和维护及结构整体性能好的特点,因此成为城市轨道交通中广泛应用的桥型[1-2]。由于梁体和桥墩直接固结,桥梁受到混凝土的收缩徐变和温度变化的影响比较大,同时桥梁的弯矩分配由梁体和墩柱的相对刚度决定,所以必须设计合理的桥墩形式和尺寸。理想的桥墩设计中,在保证桥墩承载力的前提下,应使墩柱具有较高的柔性[3-5]。城市轻轨桥梁一般会经过市区,与既有道路系统频繁交叉,存在发生汽车撞击桥墩事故的可能,事故严重时甚至会引起桥梁垮塌。据统计,美国1989年到2000年间发生了59起由撞击引起的桥梁倒塌事故[6],即使梁体没有发生完全塌落,上述柔性桥墩设计也有可能致使主梁产生过大的振动和位移,影响线路的平顺性,进而对列车行车安全构成威胁[7]。因此,有必要对撞击荷载作用下的整体式刚构桥的动力响应和桥上列车的走行性进行研究分析。目前仅有极少的研究是针对撞击荷载引起的桥梁振动和列车行车安全问题进行的。DU 等[8]以修正拉格朗日法和CR 算法建立了考虑大变形的初始斜拉桥模型,在此基础上模拟车桥耦合、船桥撞击及桥-车-船共同耦合振动,并用已知模型和数据验证了该算法的准确性,计算结果显示,当列车到达主桥塔位置时船舶的撞击作用威胁最大。夏超逸[9]建立了撞击作用下的车桥耦合系统动力分析模型,以哈大高速铁路某连续箱梁桥为研究对象,将流冰撞击和船舶撞击下的撞击力时程输入到分析模型中,分析研究了撞击荷载类型、撞击强度、列车类型和列车速度等对桥上列车行车安全的影响。崔堃鹏[10]借助车-线-桥耦合动力实验平台进行模型试验,定性研究了横向撞击力对桥梁和列车行车安全的影响规律,结果显示撞击过程中桥梁和列车的动力响应均有一定程度提高。夏超逸等[11]将船舶撞击力时程作为外部激励输入到车桥系统中,分析了某双线连续梁的桥墩遭受船舶撞击时的桥梁和列车动力响应,结果表明撞击作用使得桥梁动力响应和列车的行车安全受到了显著影响。李鹏浩等[12]使用精细化有限元模型模拟计算了流冰撞击桥墩的过程,得到了不同冰排特性下的撞击力时程曲线,并以该撞击力荷载作为外激励,计算了冰击荷载下的桥梁子系统和车辆子系统的动力响应。综上,既有研究一般将撞击荷载当作外加激励,直接输入到车桥动力分析模型中以计算撞击作用下的车桥耦合振动响应,类似方法将撞击作用下的桥梁视为弹性结构,但实际撞击作用下的桥梁变形是一个复杂的非线性过程,因此按该类方法计算得到的桥梁撞击位移难以反映桥梁实际的撞击变形特征。鉴于既有研究现状的不足,以某整体式刚构桥为例,首先运用MSC 有限元软件,模拟计算了某整体式刚构桥在6轴重载货车撞击桥墩作用下的整桥动态变形曲线,桥梁和货车均考虑了在撞击过程中的非线性变形。再将该曲线叠加到轨道不平顺中以计算分析将撞击荷载作用转化为动态不平顺的车桥耦合模型的空间振动响应,方法可为撞击荷载作用下桥上行车安全性分析研究提供参考。
1 桥墩受撞击作用下的动态非线性不平顺
本文以某轻轨线路上4×40 m 的4 跨整体式刚构桥为研究对象,其立面示意图及各桥墩相应编号见图1(a),其主梁为箱型截面,截面尺寸见图1(b);桥墩高14.5 m,截面为矩形,边墩顺桥向宽0.8 m,横桥向长2.6 m,中墩顺桥向宽1.4 m,横桥向长2.6 m,示意图见图1(b)。
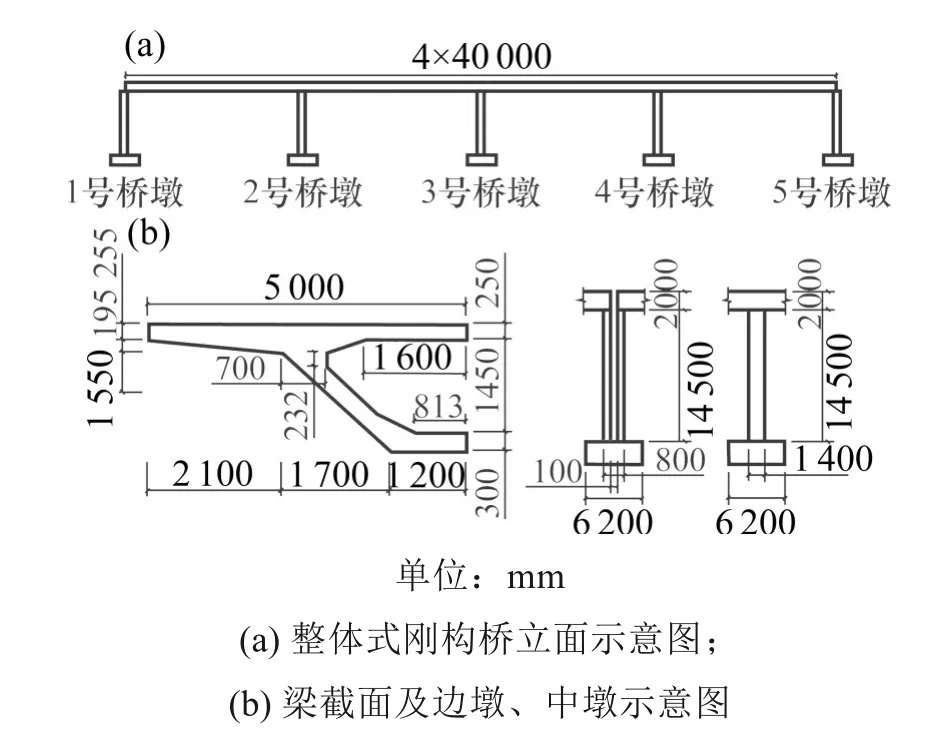
图1 整体式刚构桥示意图Fig.1 Diagram of integral rigid frame bridge
由于撞击物与桥墩的碰撞以及其与桥梁上部结构的相互作用机理十分复杂,难以从理论上获得解析解[13-14],而车桥碰撞足尺实验代价又过于昂贵,仅有少数研究可以参考[15-17],故本文使用数值模拟的方法计算货车分别撞击桥梁的边墩(1 号桥墩)和中墩(3 号桥墩)时桥梁的动力响应,然后将得到的桥面位移时程曲线叠加到桥面附加动态不平顺中,形成动态轨道不平顺,以此考虑撞击作用对车桥耦合系统动力响应的影响。
在进行数值模拟计算时,桥梁按实际参数建模,建立弹性材质的分层壳单元以模拟上部结构的C60 混凝土变截面箱梁;桥墩墩身为矩形截面,其C50 混凝土设置为实体单元,且选取为Kent-Park 非线性模型,并按Hillerborg 模型考虑其开裂的情况,HRB400 钢筋按梁单元建模并设置为Esmaeily模型。货车采用壳单元建立了一个外部尺寸长宽高分别为20,2.5 和4 m 的模型以模拟49 t重的6轴重载货车,且由于车辆发生撞击时主要是车头产生变形,因此将整车模型分为车头和车身2部分,车头采用理想弹塑性材料,车身设置为弹性材料。钢筋和车头的应变率敏感性本构方程均采用Cowper-Symonds 模型。在模拟中使货车以60 km/h 的撞击速度及20°的撞击角度分别撞击边墩和中墩,采用主从面接触算法和库伦摩擦模型计算碰撞全过程,计算步长0.005 s,计算总时长10 s。
当中墩以及边墩分别被撞击时,各跨产生的最大横向位移的信息见表1。考虑到撞击发生的概率,本文仅按撞击作用下可能的最不利振动变形进行车桥耦合振动计算,选定的计算工况汇总见表1。
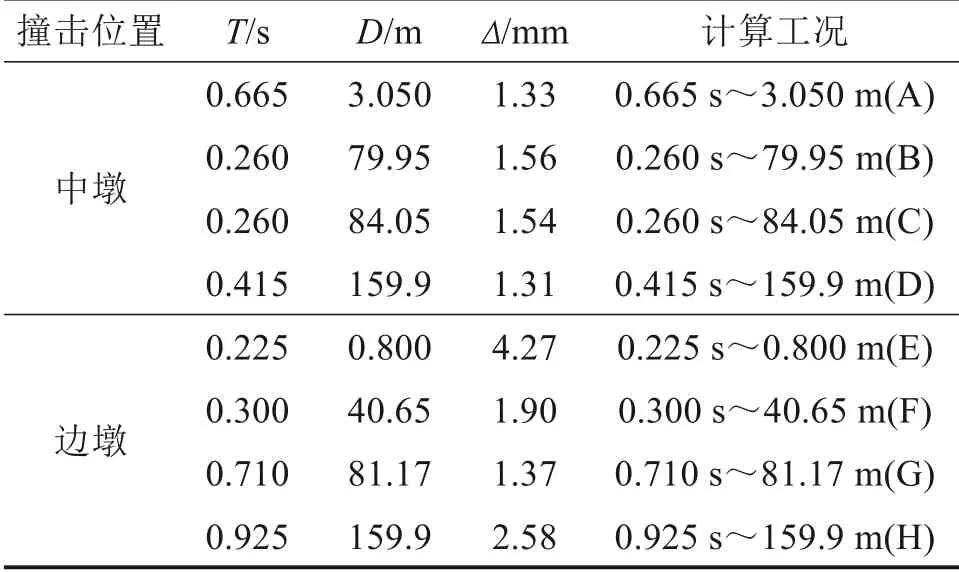
表1 撞击作用下桥梁各跨最大位移Table 1 Maximum displacement of each span of bridge under impact
根据表中桥梁振动位移各峰值发生的时刻和对应的桥面位置,进行考虑响应动态峰值的车桥耦合振动瞬时分析。即将计算得到的10 s内的全桥实时撞击位移以0.005 s 步长与原始轨道不平顺叠加生成实时动态不平顺,以便在车桥耦合振动计算时调用,并在计算时根据响应动态峰值进行调整,使得头车在到达对应跨产生振动峰值的桥面位置时调用的是相应时刻的动态不平顺。例如在工况0.665 s~3.050 m(各工况在下文中均以对应简称代替)中,当头车到达第一跨的位移最大处,即离桥头3.050 m 的位置时,调用的是撞击发生后第0.665 s的动态不平顺。
表1中各工况下对应峰值时刻的桥面横向位移X,叠加位移后的动态不平顺及原始轨道不平顺O见图2,轨道不平顺采用美国6 级轨道不平顺[18],各工况简称及各工况的最大位移点标于图内,图中x代表与桥头之间的距离,y代表横向不平顺幅值。
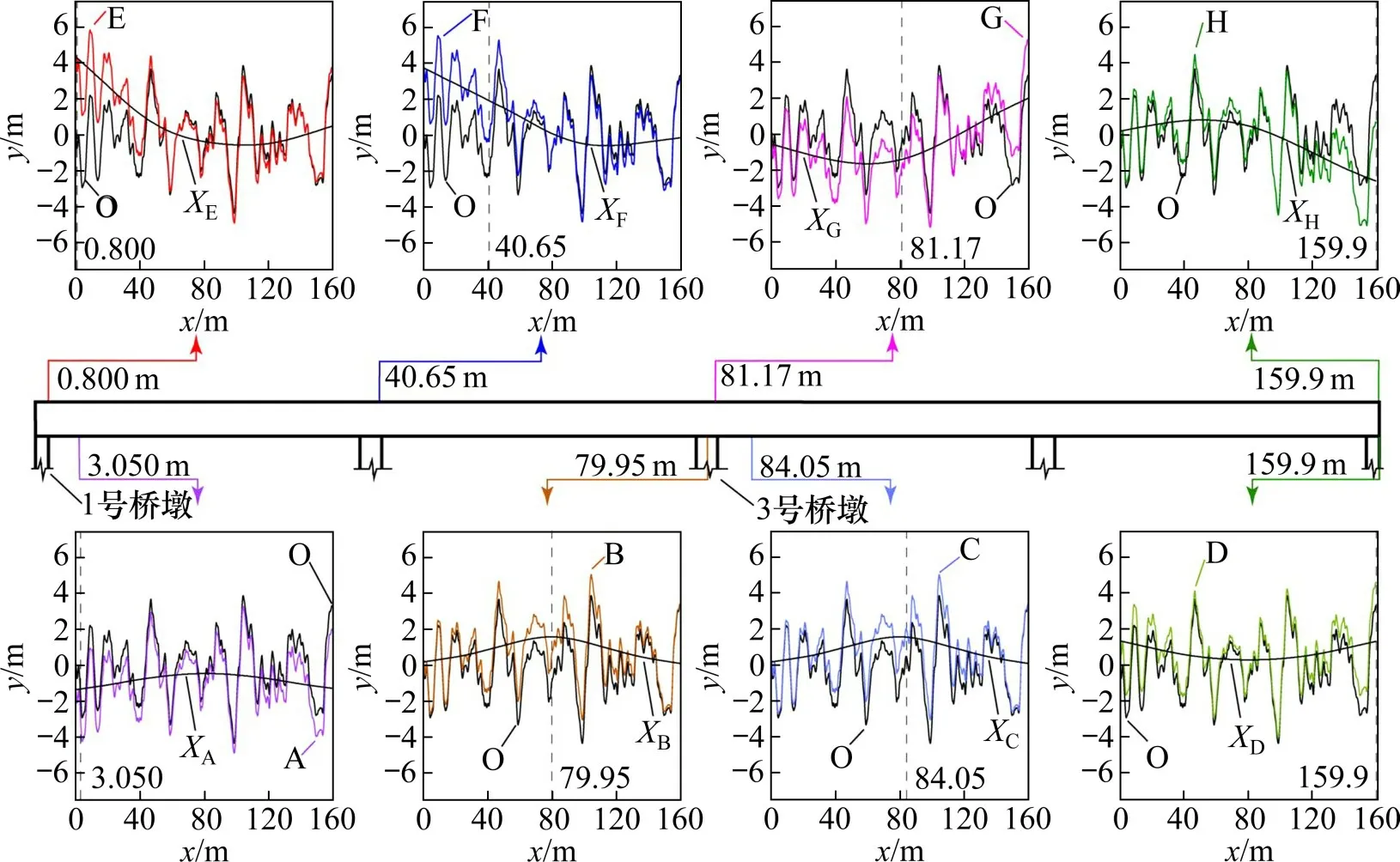
图2 撞击作用下动态不平顺示意图Fig.2 Diagram of dynamic irregularity under collision
从图中可以看出,整个撞击过程中的横向位移曲线的最大波峰会在撞击发生后产生在靠近撞击点的梁体区域,这种波峰会随着时间推移如同波浪一样向相邻几跨移动,并且其峰值会因为能量损耗而不断减小。此外,当边墩受撞击时的桥梁的振动响应比中墩受撞击时对应的桥梁振动响应大。
2 桥墩受撞击作用下车桥系统空间振动分析模型
2.1 桥梁模型
利用基于文献[19]原理开发的有限元分析软件进行桥梁模型的建立。全桥构件均采用空间梁单元建模,并采用m 法考虑桩土之间的共同作用,建立的模型如图3(a)所示。
2.2 列车模型
针对复杂的列车模型,采用以下假定进行简化:1) 车体、轮对和转向架为刚体,且只产生小位移振动;2) 列车匀速通过桥梁;3) 车辆模型中的所有弹簧都按线性处理,蠕滑力按线性计算,所有阻尼都按黏滞阻尼计算;4) 轮轨关系为密贴模型;5)忽略轮对的侧滚和点头运动。
按照以上假定,可以建立一个23 自由度的4轴列车模型,如图3(b)所示。
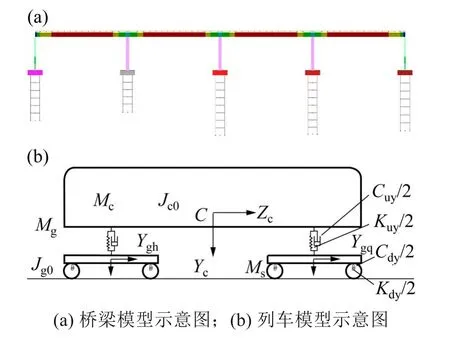
图3 桥梁及列车模型Fig.3 Bridge and train model
其中车体和转向架有侧滚、侧摆、浮沉、摇头和点头这5个自由度,每个轮对有侧摆和摇头这2 个自由度。图中各参数含义和模型矩阵方程的具体演引过程参考文献[20]。
计算中运行列车选定为地铁B型车,静轴重为140 kN,采用2×(1动+1拖+1动)的编组,设计车速为120 km/h,计算车速选取为90~140 km/h。
2.3 撞击作用下车桥系统耦合振动方程的建立和求解
要模拟计算t时刻的车桥时变系统的空间振动,必须得到在该时刻系统的总势能Πd(t),即t时刻行驶于桥上的所有车辆的总势能Πv(t)及桥梁所有构件的总势能Πb(t),运用弹性系统动力学总势能不变值原理δΠd(t)=0 外加形成矩阵的“对号入座”法则,可得到车桥系统的矩阵方程。按照该思路,建立的撞击作用下车桥系统耦合振动模型见图4,对应t时刻的振动方程如下:
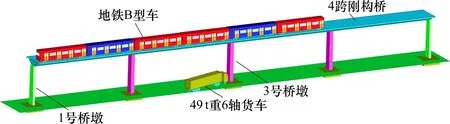
图4 桥墩受撞击作用下车桥耦合振动模型Fig.4 Model of vehicle-bridge coupled vibration when pier is impacted
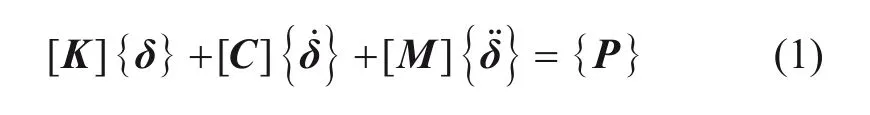
式中:[K],[C]和[M]分别表示系统的刚度、阻尼和质量矩阵;{P}表示系统的荷载列阵;{δ},{}和{}分别表示系统的位移、速度和加速度列阵。将前文得到的动态不平顺代入对应参数,则位移列阵可以拆分为k个已知参数和n个未知参数,即{δ}={δk δn}T,则式(1)可以重新表示为:
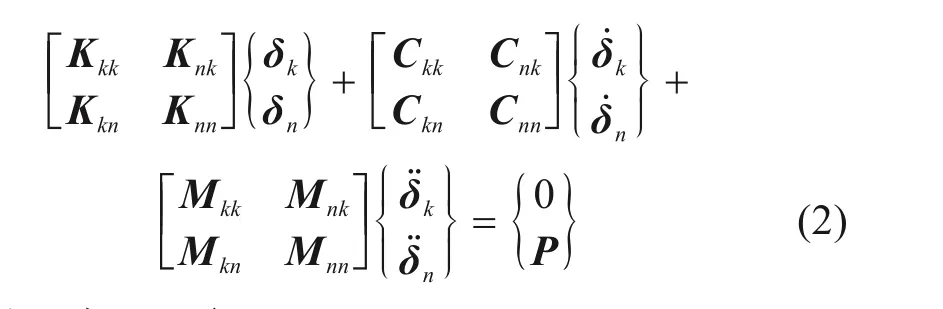
展开式(2)可得:
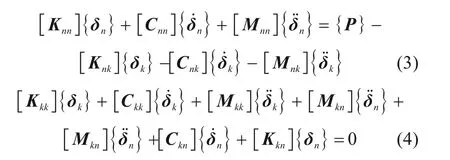
很显然,式(4)属于非独立的矩阵方程,可以将其省去。然后对式(3)采用逐步积分法进行求解,可以得到在撞击作用下的车桥耦合系统的动力响应。
3 桥墩受撞击作用下列车动力响应
当货车撞击桥墩时,由于这种荷载只会作用很短的一段时间,可以不用考虑其对车体加速度和乘车舒适度的影响[21],因此本文仅考虑脱轨系数、轮重减载率和轮对横向力这3 项安全性指标。根据GB50157—2013(《地铁设计规范》)[22]的有关规定,脱轨系数Q/P,轮重减载率ΔP/和轮对横向力Q应满足:

式中:Q为轮对一侧的车轮的横向力;P为轮对一侧的车轮的垂直力;ΔP为一侧车轮的轮重减载量,为车轮的平均轮重;P0为静轴重,计算可得轮对横向力限值为56.67 kN。
根据前述条件对选定的工况及无撞击条件下的列车过桥耦合振动响应进行仿真计算。
各工况下动车最大响应随车速增加的分布规律如图5 所示,d代表脱轨系数,w代表轮重减载率,Q代表轮对横向力,v代表列车速度,N工况即无撞击工况。
从图5 中可以看出,由于在中墩遭到撞击时,桥梁位移响应较小,因此对应的列车响应基本不受影响,最大脱轨系数分布变化很小,其最值由无撞击工况下的0.08 增加到0.085;而边墩遭到撞击的工况F,G 对应的脱轨系数分布规律显示此时的列车横向振动受到撞击的强烈影响,最大脱轨系数从无撞击工况下的0.08 分别增加到0.145 和0.137。
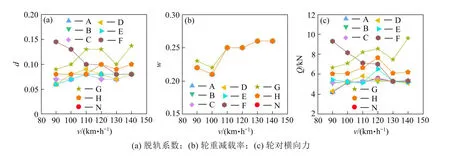
图5 动车响应随车速增加的分布Fig.5 Distribution of motor-car response vs train speed
无论是中墩受撞击还是边墩受撞击,最大轮重减载率的分布规律基本没有变化,对应最值没有增加,即在无撞击时是0.259,受到撞击时仍为0.259。
轮对横向力的变化规律与脱轨系数相似,当中墩遭到撞击时,其最值从5.62 kN 增加到5.83 kN;在边墩受到撞击的F,G 工况下,其最值分别增加到9.31 kN和9.62 kN。
3 项指标的计算结果分别小于0.8,0.6 和56.67 kN的安全限值。
工况D,E 和H 下对应的最大脱轨系数出现在列车编组的第1 辆列车,F 和G 则出现在第3 辆列车和第4辆列车,对应的时程曲线如图6所示,t代表时间。

图6 脱轨系数时程曲线Fig.6 Derailment coefficient time history curves
从图6中可以看出,当撞击发生后,动车的脱轨系数会随着撞击作用下的桥面位移振动产生振荡,且变化趋势与动态不平顺波形基本一致。在撞击响应尚未迅速衰减的短暂时间内,工况D 下,由于中墩受撞击时的梁体响应较小,脱轨系数仅产生小幅度振荡;工况E,F,G 和H 下,由于边墩受撞击时的梁体响应较大,撞击作用在耦合振动中起主导作用。
当边墩受到撞击后,第1跨会在一段时间内产生较大的撞击振动,对行驶在其上的列车产生明显影响。反映到图6 中,工况E 下的第1 辆列车到达第1跨位移最大点时,其脱轨系数有很明显的增长,从0.022增加到0.074,但由于此时并非该工况下的最不利情形,因此该工况下的最大脱轨系数未受到影响,依然出现在列车行驶的后半段。工况F 下的第1 跨位移维持在较大时,正好是列车编组的第3辆列车在其上行驶,因此其脱轨系数为该工况下最大值,当其在撞击发生后的0.334 s 上桥时,第1跨的位移还未明显衰减,对应的脱轨系数产生了一个波峰突变;同理,工况G 下列车编组的第4 辆列车在撞击发生后的0.188 s 上桥时,第1跨的位移虽未达到峰值,但依然较大,达到3.647 mm,因此脱轨系数也产生了一个对应的波峰突变,是该工况下的最大值。对于工况H 而言,当撞击发生时头车位于离桥头129 m 的位置,且正驶离撞击点,由于梁体振动波峰从撞击点向外扩散的滞后性,列车运行仅受其小幅度干扰,因此脱轨系数时程曲线在撞击发生后的一段时间内仅有小幅度振荡;当振动波峰传递至列车附近时已有减弱,因此脱轨系数时程曲线在后半段有较明显的波动,但其幅度比工况E,F和G都要小得多。随着列车前进,撞击位移迅速减小,动车的响应回落到无撞击时的时程曲线上。
上述规律符合撞击荷载下车桥耦合系统的响应特点,表明考虑动态不平顺的车桥系统模型可以很好地反映撞击作用对车桥系统耦合振动的影响,同时根据动态不平顺的幅值可以直观地判断撞击作用下列车运行在桥上何处时将会遇到危险。
工况D和F下车速140 km/h时的轮重减载率时程曲线如图7所示。
由图7可知,无撞击时的轮重减载率时程曲线和有撞击时的基本重叠,表明撞击对列车的竖向振动基本没有影响。
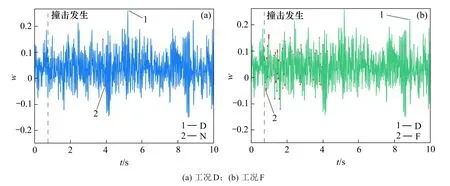
图7 轮重减载率时程曲线Fig.7 Time history curves of wheelset load reduction rate
工况D 下车速110 km/h 时和工况E 下车速120 km/h时的轮对横向力时程曲线如图8所示。
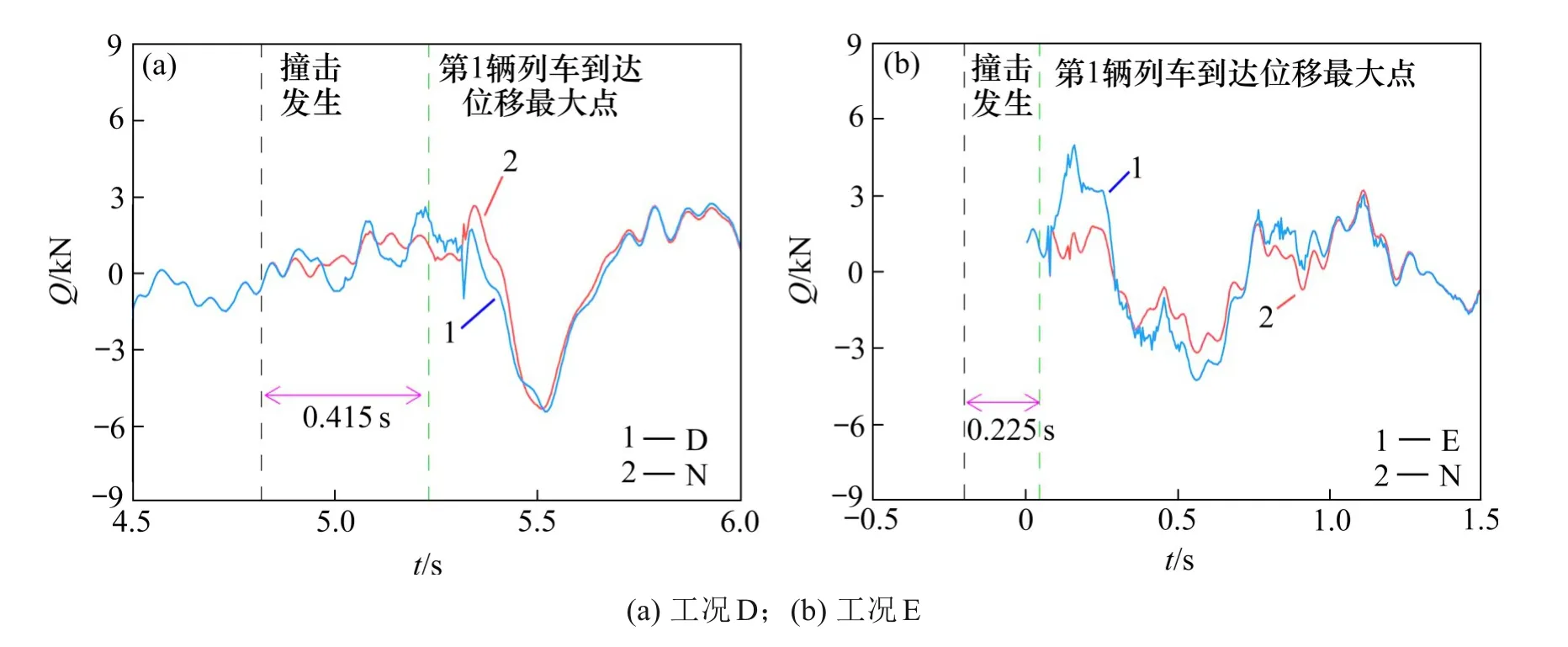
图8 轮对横向力时程曲线Fig.8 Wheelset lateral force time history curves
轮对横向力时程曲线的波动趋势及其反映的规律与脱轨系数基本一致。
4 结论
1) 当桥墩受到撞击时,梁体的最大撞击位移会产生在撞击点附近,其振动随时间如同波浪一样从撞击点向两侧扩散,振动峰值不断减小。
2) 基于动态不平顺的车桥耦合系统模型考虑了撞击过程中桥梁变形的非线性,并能够更直观地反映撞击荷载对车桥系统耦合振动的影响,可为研究撞击作用对车桥耦合振动的影响提供参考。
3) 计算结果表明,桥墩受到撞击时,若列车运行在撞击点附近,则其横向振动将受到不可忽视的影响,而竖向振动受到的影响甚微;而当列车不在撞击点附近时,列车的运行不会受到很大影响。此外,当桥梁边墩受到撞击时,桥上列车的响应更大,此时更易发生事故。
