塑料排水板地基变形的简易计算法

彭扬发，周洋，王宁波，徐方, ，阮波, ，叶新宇，冷伍明

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 河南工业大学 土木建筑学院，河南 郑州 450001；3. 湖南铁院土木工程检测有限公司，湖南 长沙 410075)

随着我国国民经济的快速发展，建于软土地区的基础设施(如铁路、公路和机场等)不断增多并趋于密集。由于软土地基具有压缩性大、含水量高、强度低和透水性差等特点，修建设施前通常需要对其进行加固或处理[1-2]。其中，塑料排水板结合预压处理法以其工期短、无需大型施工机械、成本低及环境友好等优点而得到广泛应用[3-4]。排水板地基的固结和变形计算分析，是工程设计中需要考虑的关键问题[5-7]。BARRON 等[8-9]在考虑排水板地基涂抹效应和井阻效应的前提下，基于等应变假设和圆柱形单元体分别推导了不同形式的排水板地基固结解析解，亦是目前工程界最常采用的排水板地基固结分析方法。近年来，亦有诸多学者基于不同的侧重点发展了排水板地基的固结理论。ZHOU 等[5]提出了考虑真空预压过程中排水板淤堵效应的排水板地基固结分析的解析法；WANG 等[6]建立了考虑真空压力沿圆柱形单元体径向衰减的排水板地基大变形固结模型；NGUYEN等[7]进一步推导了考虑软土蠕变效应的排水板地基固结解析解；YU 等[10]提出了考虑排水板排水性能随时间衰减的排水板地基固结解析解；周洋等[11]提出了排水板地基不均匀固结效应的简易量化法；张玉国等[12]提出了考虑土体径向渗透系数变化的真空预压排水板地基的固结解析法；田乙等[13]基于椭圆柱排水体等效假定，并考虑真空压力在排水板内的线性衰减规律，推导了真空预压下排水板地基的水平向(即径向)固结解析解；卢萌盟等[14]将矩形截面的排水板转换为圆环形截面，并提出了相应的固结解析解。上述研究基于不同的出发点发展了排水板地基的固结理论；然而，预压荷载下，排水板地基内的孔隙水总会沿着相对容易的排水路径排出。因此，在表面排水垫层形成的竖向排水边界和塑料排水板提供的水平向排水边界的共同作用下，排水板地基表层一定厚度土体将同时在竖向和水平向排水固结，而当地基深度超过一定深度时，土体可近似认为只在水平方向排水固结[15]。可见排水板地基的表面排水垫层存在其有效影响深度。计算排水板地基的固结过程和沉降历史时，应考虑该双向排水固结层的影响效应，但现阶段并无方法可有效计算该影响层的厚度。此外，工程实践中预压荷载(如堆载)通常是随施工过程逐步施加的，预压荷载的施加历史很大程度上影响着排水板地基的固结过程。对此，部分学者先后提出了计算时变荷载下排水板地基固结度的解析法，然而相关解析解通常以复杂的无穷级数形式或拉普拉斯变换形式给出[16-17]，不便于工程应用。鉴于上述研究现状，本文首先推导了排水板地基表面双向固结层厚度的近似计算公式，并基于排水板地基有效应力变化的连续性，发展了一种时变荷载下排水板地基固结度的计算方法。其次，结合软土地层的压缩特性，建立了预压荷载下排水板地基沉降-时间曲线的实用分析法。最后，将本文的固结度和沉降计算方法拓展应用于排水板地基侧向变形的预测计算，综合形成了排水板地基变形计算的简易法。

1 双向固结层厚度的确定方法

对排水板地基而言，当地基达到一定深度时，土体距离表面排水垫层已较远，而距离竖向打设的排水板则较近，此时超孔隙水压可近似认为只沿塑料排水板提供的水平向排水路径消散。因此，可将水平向排水引起的固结度(Uh)等于竖向排水引起的固结度(Uv)的深度作为确定排水板地基表面双向固结层厚度(Hd)的依据。根据HANSBO[9]提出的排水板地基固结理论，Uh可按下式计算:

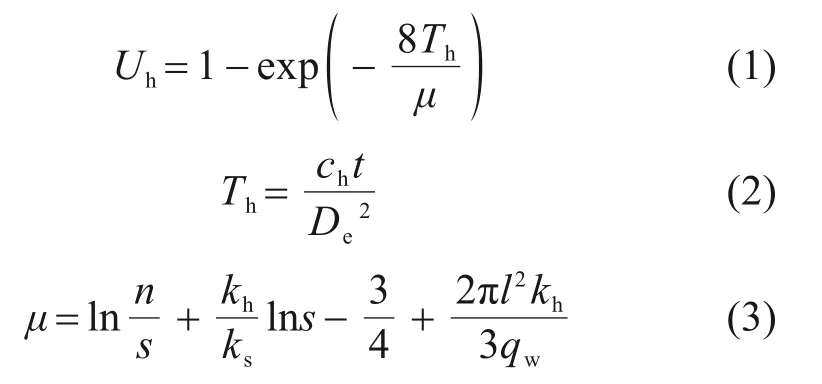
式中：n=De/dw；s=ds/dw；Th为径向固结的时间因素；t为固结时间；l为排水板的长度；qw为排水板的排水量；ch为土体在水平方向的固结系数；dw，ds和De分别为排水的等效直径、涂抹区的直径和圆柱形单元体的直径；kh和ks分别为原状土和涂抹区土体的水平方向渗透系数。

CHAⅠ等[18]提出了TERZAGHⅠK[19]一维竖向固结理论的近似表达式，避免了竖向固结度分析中的无穷级数计算过程，给出的Uv近似公式如下：

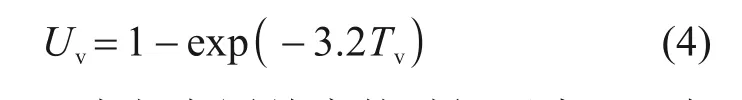
式中：Tv(=cvt/H2)为竖向固结度的时间因素；cv为土体在竖向的固结系数；H为土层厚度。

令Uh=Uv，可推导得到排水板地基中表面双向固结层厚度Hd的计算公式如下：

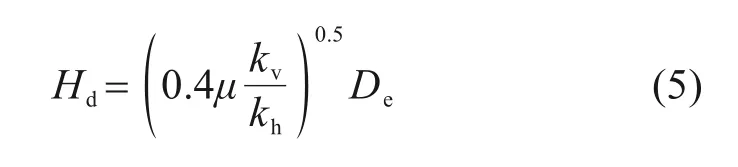
式中：kv为原状土的竖向渗透系数。

由式(5)可知，双向固结层的厚度Hd与排水板和地基土的参数有关。实际工程中，地基土和排水板的特性通常是预先确定的，而De，ds和kh/ks则可能随排水板的设计间距和打设方法而变化。工程中通常采用横截面长100 mm，宽为3～5 mm 的矩形截面排水板，换算所得排水板等效直径dw约为52 mm。排水板一般由插排机上的金属芯棒辅助插入地基，并按梅花形或矩形布设，间距多为1.0～1.5 m，对应的圆柱形单元体直径De约为1.05～1.70 m。打设排水板时引起的地基涂抹区直径ds约为金属芯棒等效直径dm的2～3 倍或排水板等效直径dw的4～6 倍[20-21]；工程中，ds的值一般在0.25～0.35 m。基于上述分析，本文采用表1 中土层1 参数和表2 中排水板参数分析De，ds和kh/ks对双向固结层厚度Hd的影响，其中E为土层的弹性模量。

表1 土层参数Table 1 Soil properties

图1 为分析所得表面双向排水垫层厚度Hd随De，ds和kh/ks的变化关系曲线。由图1 可知，Hd随De，ds和kh/ks的增加而非线性增大。De，ds和kh/ks的增大意味着径向排水引起的固结速率相对减小，表明Hd主要与竖向排水固结和径向排水固结的相对重要性有关。另外，当kv/kh为0.5 时，由式(5)计算所得的Hd约为圆柱形单元体直径De的0.9～1.1倍；因此，对于kv/kh为0.5 的土层，其表面双向排水固结层的厚度Hd可近似取为De。

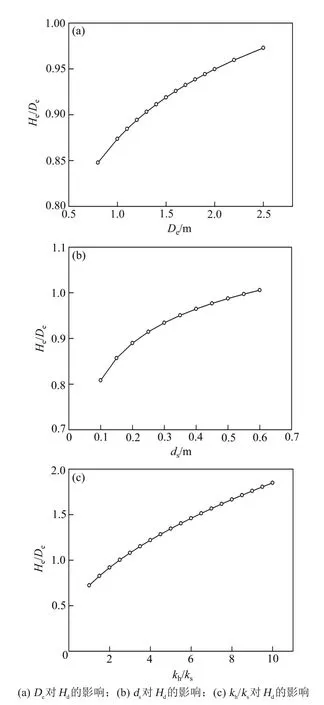
图1 De,ds和kh/ks对Hd的影响Fig.1 Effects of De，ds and kh/ks on Hd

2 时变荷载下排水板地基固结分析的实用法

根据排水板地基有效应力变化的连续性，提出采用阶梯型等效荷载模拟实际的堆载预压过程(见图2)，并通过如下步骤计算排水板地基的固结度U：

1) 假设ti时刻施加的预压荷载为pi，pi对应的固结度为Ui。在ti时刻瞬时施加一个增量荷载Δpj，此时总荷载pj=pi+Δpj，则pj所对应的固结度Uj可近似计算为：

2)根据Uj和相应的固结理论(如Hansbo径向固结理论[9])可反算得到与pj对应的等效固结时间tj0；

3)ti+Δt时刻，荷载pj作用下的固结度则可根据相应的固结理论和等效固结时间tj0+Δt计算。

图2 中时变荷载线末端3 个三角形的面积满足Ak=Ai+Aj；除此之外，线性时变荷载线上方和下方各三角形的面积相同，以此满足阶梯型等效荷载在加载线上方和下方的三角形总面积相等。

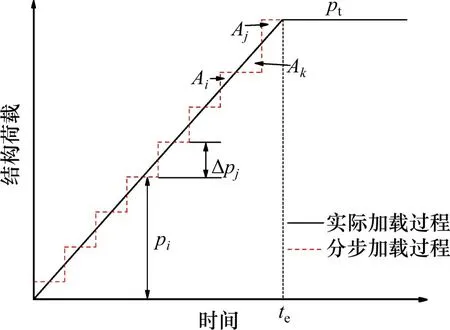
图2 阶梯型等效荷载加载过程Fig.2 Equivalent stepwise loading process

针对以上提出的时变堆载的阶梯型等效法，需要进一步分析探讨阶梯型等效荷载加载步的合理划分数量。对此，本文开展了排水板地基圆柱形单元体的系列轴对称有限元仿真分析(FEA)，并将有限元计算所得固结度与本文方法对比，综合评估本文方法的有效性。采用Plaxis 2D 有限元软件模拟分析了2类模型场地，轴对称模型的半径均为0.75 m；其中一类由5.0 m 厚的单一土层组成(图3(a)，称为A 型)，另一类由2 层各厚2.5 m 的土层组成(图3(b)，称为B 型)。为满足有限元仿真过程中土体的渗透系数和固结系数与理论公式计算所采用的值始终保持一致，便于数值仿真所得固结度与本文方法所得固结度的直接对比，模型地基采用线弹性模型，土层1 和土层2 的参数见表1，排水板参数见表2。

有限元模型的左侧定义为透水边界(该处有排水板)，并根据表3 中所列工况决定模型的顶部和底部是透水或不透水边界。表3排水边界一栏中的H 表示仅有径向排水的工况，H+1V 表示径向排水和单面竖向排水工况，H+2V 则表示径向排水和双面竖向排水工况。图3 为2 类模型地基的有限元网格图，其中模型地基表面处施加的线性时变预压荷载的最终值均为80 kPa，但根据不同的工况加载速率按10，4和1 kPa/d施加。

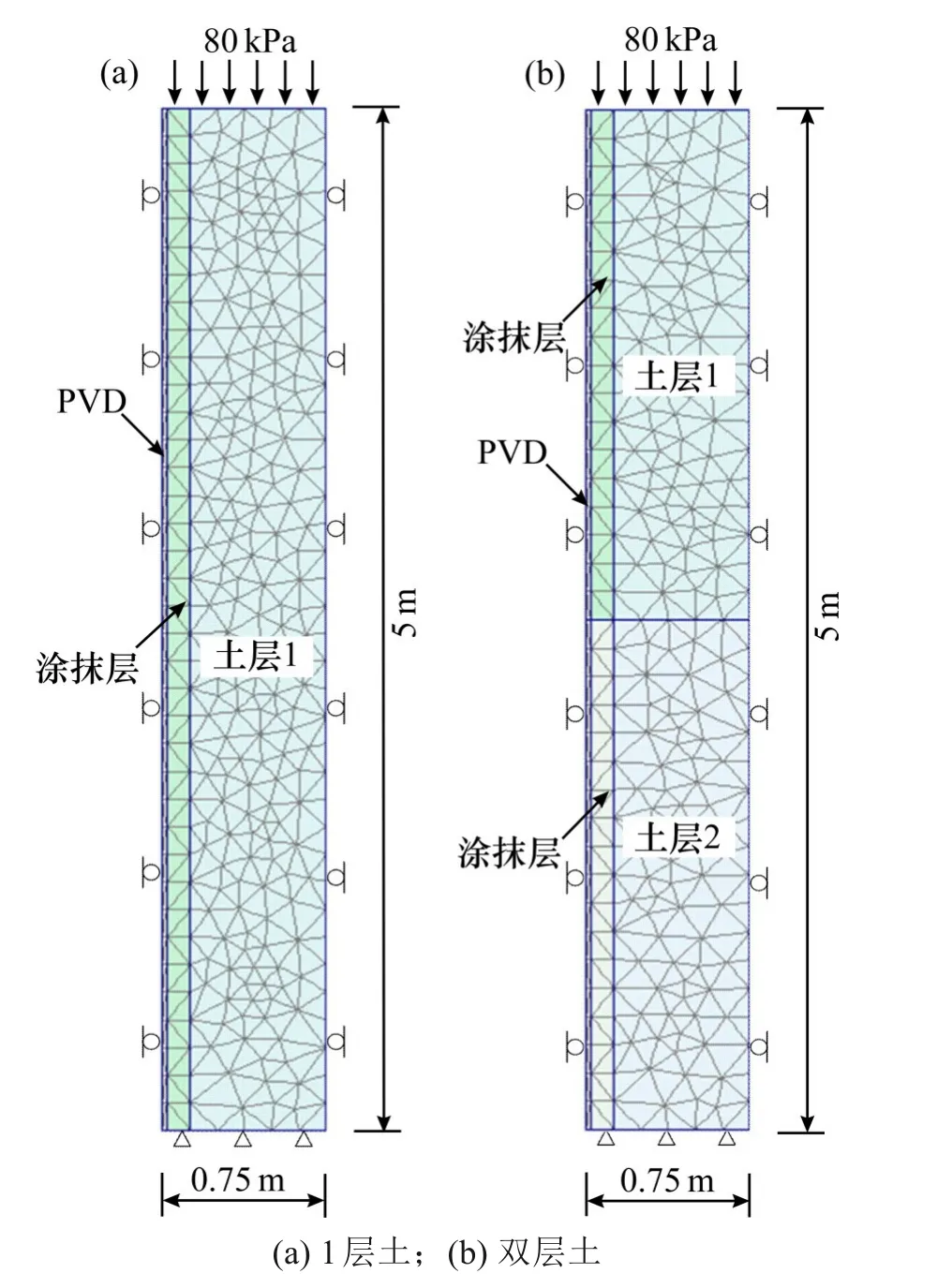
图3 模型地基网格Fig.3 Mesh of model grounds

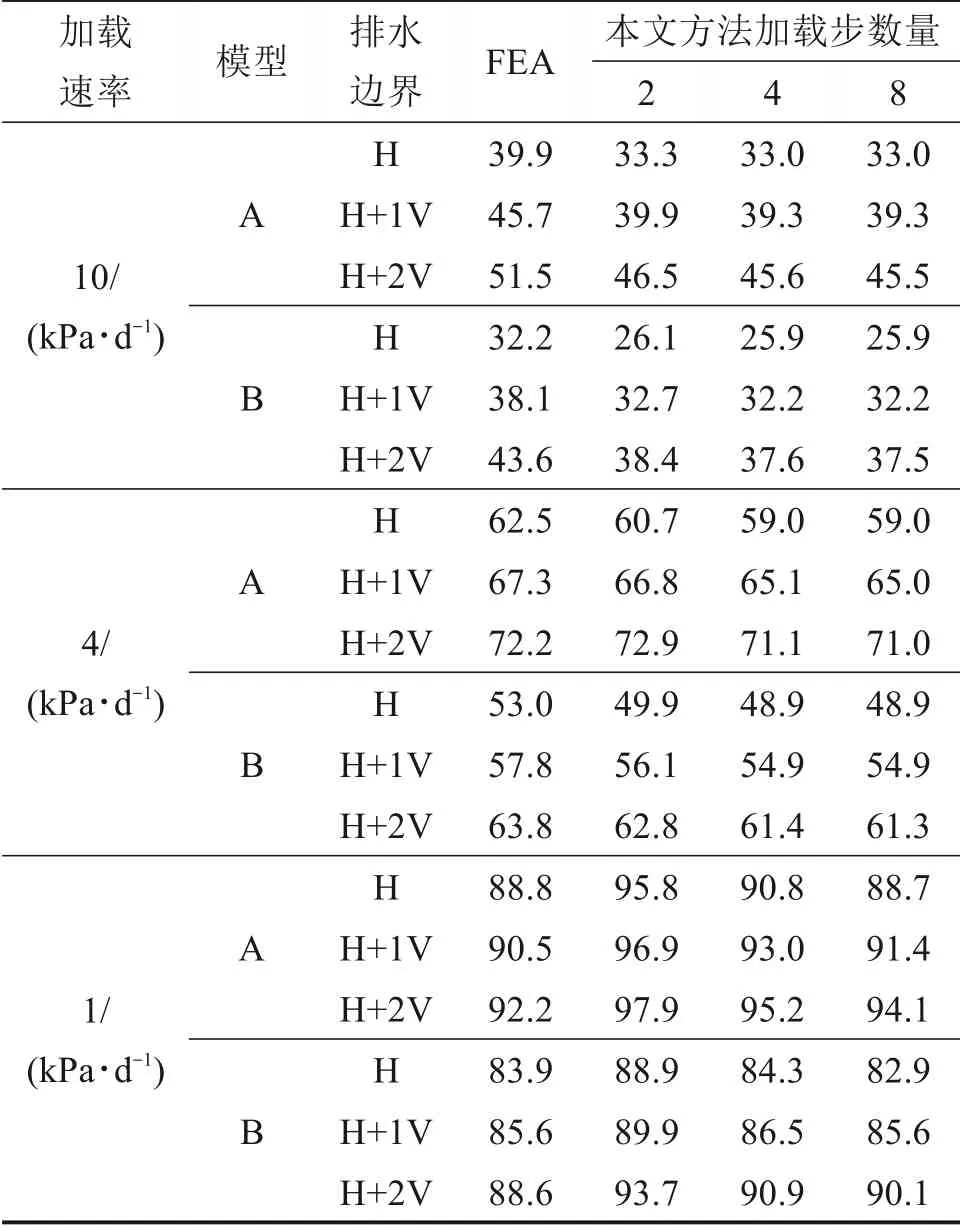
表3 不同方法计算所得固结度Table 3 U values from different calculation methods %

表3列出了本文方法和有限元仿真计算所得的加载结束时刻(即图2 中te时刻)模型地基的平均固结度。本文方法中，根据式(5)计算所得的表面双向排水固结层厚度Hd为1.38 m，采用TERZAGHⅠK[19]一维竖向固结理论和HANSBO[9]径向固结理论计算竖向和径向排水效应引起的固结度Uv和Uh，并根据CARⅠLLO[22]提出的方法按式(7)计算表面双向固结层的最终固结度U：

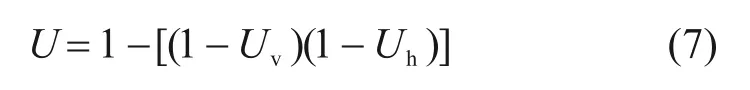
对于双向固结层以外的土层只需考虑径向排水效应，则采用HANSBO[9]的径向固结理论计算其固结度。最后，根据各土层厚度计算整个模型地基的加权平均固结度。由表3可知，线性时变荷载按阶梯型等效荷载法分4 步和8 步施加所得的固结度相差甚微，但与分2步施加的工况所得固结度相比则存在较大差别，表明采用本文提出的阶梯型荷载等效法计算时变荷载下排水板地基的固结度时，阶梯型荷载的划分步数不宜小于4步。

图4 为本文方法(分4 个加载步)和有限元仿真计算所得固结度的对比结果。由图4可见，本文方法与有限元仿真计算总体吻合较好，最大误差小于10%；特别当模型地基的固结度U超过50%时，本文方法与有限元计算结果基本一致(误差在5%以内)。塑料排水板地基的固结速率通常比天然地基大得多，既有研究表明堆载结束时刻排水板地基的固结度一般可达70%以上[23-24]；因此，本文提出的阶梯型等效荷载法可作为时变荷载下排水板地基固结分析的有效方法之一。

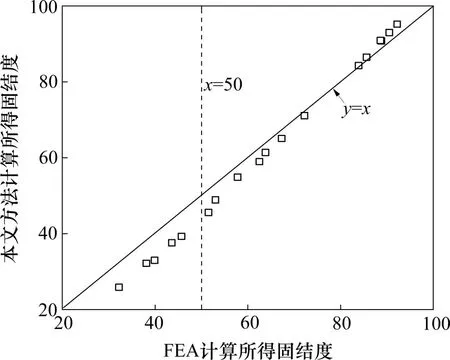
图4 本文方法与FEA模拟得到的固结度比较Fig.4 Comparison of U from FEA and the proposed method

3 排水板地基沉降-时间曲线的计算方法

时变荷载作用下排水板地基的最终沉降可根据土体的一维压缩理论及分层总和法计算求得；然而要获得排水板地基的沉降-时间曲线，则需计算不同时刻t时地基的沉降。

根据土体的一维压缩曲线，第i层土t时刻的压缩变形Si(t)与土层孔隙比的改变量Δei存在如下关系：式中：e0i为第i层土的初始孔隙比；Hi为第i层土的厚度。

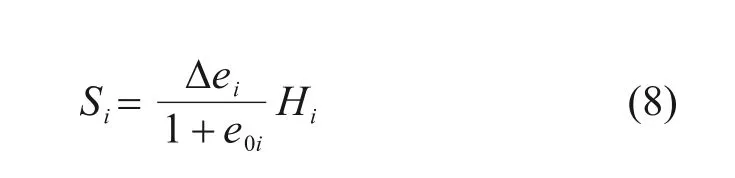
由土层的一维压缩曲线可知，土层孔隙比的改变量Δei可计算如下：

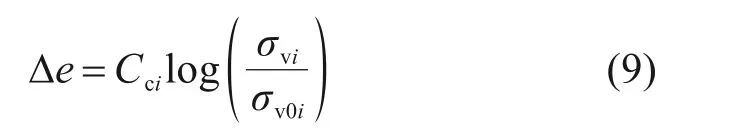
式中：Cci为第i层土的压缩指数，当土体处于超固结状态时，则用膨胀指数Csi代替Cci；σv0i和σvi分别为第i层土的初始竖向有效应力和t时刻的竖向有效应力。

运用本文提出的排水板地基表面双向固结层厚度的计算方法和时变荷载下排水板地基固结分析的阶梯型等效荷载法，可求得第i层土的平均固结度Ui，此时第i层土的有效应力σvi可根据下式求得：

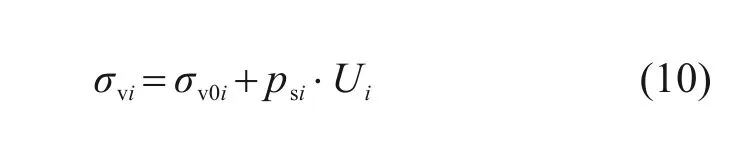
式中：psi为上部预压荷载于第i层土处引起的总附加应力，具体可根据DAS 等[25]提出的堆载下地基土的附加应力计算方法确定。

将式(10)和式(9)代入式(8)，即可得第i层土在t时刻的一维压缩变形Si(t)。最后，采用分层总和法，即可得到排水板地基在t时刻的总沉降计算公式如下：

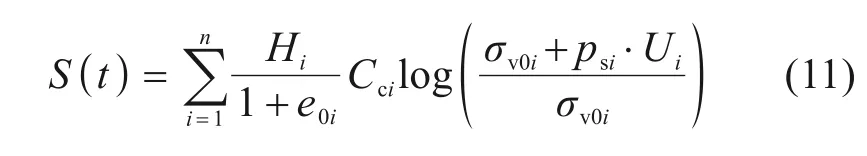
式中：S(t)为t时刻排水板地基的总沉降(即地表沉降)。具体分析时，将不同时刻计算所得的总沉降S(t)绘制为时间t的函数，即可得排水板地基的沉降-时间曲线。

4 侧向位移的预测方法

CHAⅠ等[23]基于大量工程案例数据，提出了预测真空-堆载联合预压下排水板地基最大净侧向变形(即最大向外侧向变形和最大向内侧向变形的差值)的经验方法。XU 等[24]进一步结合实例数据和模型试验拓展了上述方法，提出了堆载预压下排水板地基最大向外侧向变形的预测计算法。上述方法的核心要点是建立了排水板地基最大侧向变形和地基表面沉降比值(NLD)与表征参数RLS之间的经验关系；其中RLS的计算过程中综合考量了地基土的压缩、固结及强度特性和堆载的施加历史。参数NLD和RLS的具体计算方法如下：

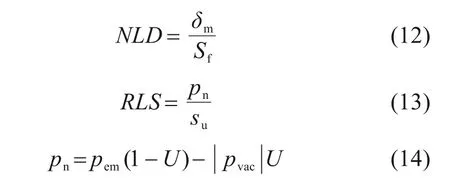
式中：δm为堆载预压下排水板地基的最大向外侧向变形；当真空和堆载联合预压时，δm则表示地基的最大净侧向变形；Sf为地表堆载中心线处的最终沉降；pem为堆载；pvac为真空荷载；su为堆载施加完成时排水板地基的平均不排水抗剪强度；U为堆载施加完成时排水板地基的平均固结度。式(13)中的不排水抗剪强度su可根据LADD[26]提出的经验方法按式(15)计算：

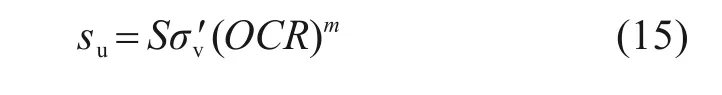
式中：σ'v为地基土的竖向有效应力；OCR为超固结比；S和m为经验常数，其中S的取值范围为0.162～0.25，m的取值范围为0.75～1.0。通常，堆载填筑完成时地基土均处于或接近于正常固结状态(即OCR=1.0)，因此常数m的影响可忽略不计。常数S则可根据原位试验获得的不排水抗剪强度su的反算获得；当无实测数据可用时，根据既有研究的相关经验[23-24]，S可初步取为0.25。

式(13)和式(14)中不排水抗剪强度su和固结度U均为堆载填筑完成(即路堤填筑完成)时刻的值。取该时刻为计算时间点的原因在于：此时地基土承受最大的预压荷载，且地基的不排水抗剪强度相对较小，该时刻通常亦是地基安全系数最小的时刻，采用此时刻的su和U值分析排水板地基的侧向变形更具代表性。XU 等[24]通过工程案例数据和模型试验分析得到的NLD和RLS之间的关系如图5所示。

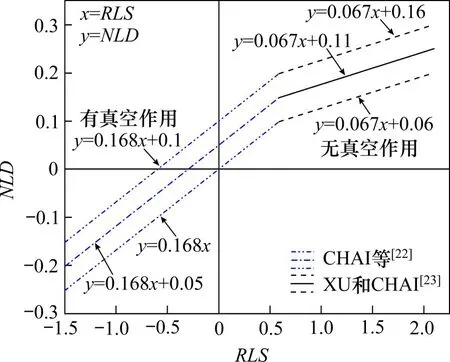
图5 NLD与RLS的关系Fig.5 Relationship between NLD and RLS

5 应用分析

5.1 工程概况

本节结合2段填筑于排水板地基之上的典型试验路堤，运用本文方法对地基的固结度、沉降和侧向变形进行计算和分析。2 段试验路堤位于四川省境内，最早由冯永财[27]于2013年报道了相关测试数据；为控制篇幅，本节主要对其中的试验路堤A 进行计算和分析。试验路堤A 的地基主要由2层厚度分别为6 m和3.5 m的软黏土层组成，2层土的kh/ks值分别为4.44 和3.75。路堤的几何形状和软黏土层的相关物理力学参数见图6；其中，e0为初始孔隙比，Es1-2表示有效应力100～200 kPa 时土体的压缩模量。地下水位位于地表以下0.5 m 处；排水板截面尺寸为100 mm×4 mm，呈三角形分布，间距为1.3 m。排水板的具体参数见表4。根据式(4)计算可得，排水板地基表面双向排水固结层的厚度为1.22 m。

表4 试验路堤A的PVD参数Table 4 Parameters of PVD for embankment A

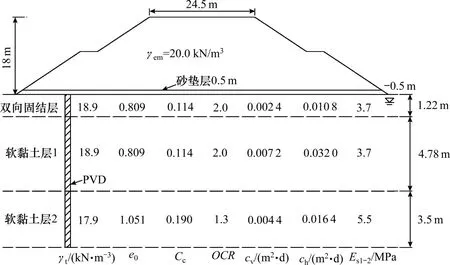
图6 试验路堤A几何尺寸及地基土参数Fig.6 Cross-section and soil parameters of embankment A

5.2 沉降分析

图7 为试验路堤A 的堆载历史，结合图6 中的地基土参数，运用本文提出的沉降-时间曲线分析方法(即式(11))计算了试验路堤A 的排水板地基沉降历史。具体分析时，地基内的附加应力根据DAS 等[25]提出的路堤荷载下地基土的附加应力计算方法确定；当土层处于超固结状态时，其膨胀指数Cs近似取为压缩指数Cc的1/10[24,28]。时变路堤堆载下，排水板地基的固结度则采用本文提出的阶梯型荷载等效法计算。图8为本文方法分析得到的排水板地基沉降曲线与实测曲线的对比；由图8可见，本文方法的计算结果与实测数据吻合较好。

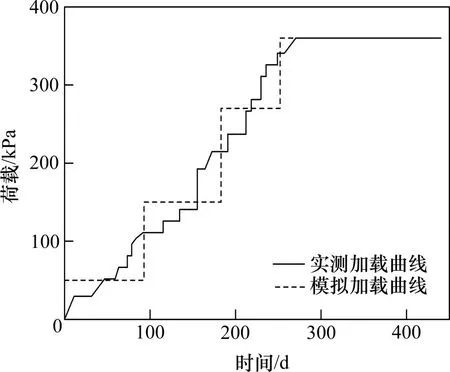
图7 试验路堤A堆载历史Fig.7 Preloading history of embankment A

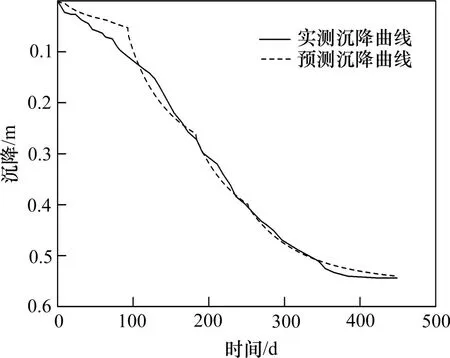
图8 试验路堤A处地表沉降-时间曲线Fig.8 Ground surface settlement curves of embankment A

5.3 侧向变形分析

预测排水板地基的最大侧向变形时，首先计算获得路堤中心处地面的最终沉降Sf，地基土平均固结度U和不排水抗剪强度su，具体计算值见表5。试验路堤A 中心线处地面最终沉降Sf的计算值为0.531 m，非常接近0.541 m 的实测值。根据式(12)～(15)及表5 中的数据可计算得到试验路堤A对应的RLS值如下：

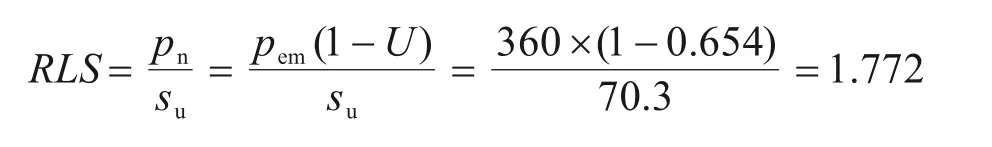
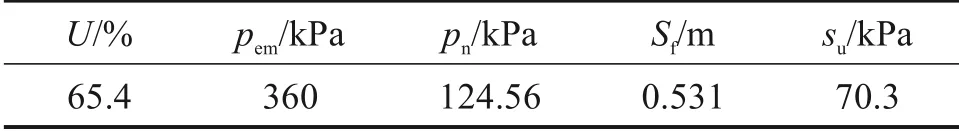
表5 侧向变形计算参数Table 5 Parameters for calculating the lateral deformation

根据XU 等[23]建立的NLD与RLS的关系(图5)，可计算得试验路堤A对应的NLD值如下：

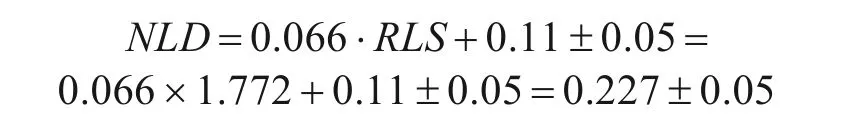
因此，试验路堤A 处的NLD预测范围为0.177～0.277。由Sf的值和NLD的范围，按式(12)可得试验路堤A 坡脚处的最大侧向变形(δm)的预测范围为0.094～0.147 m。试验路堤A 坡脚处实测的侧向变形随深度的变化曲线如图9 所示。由图9 可知最大侧向变形大致出现在地基深度2.0 m 处，其值约为0.125 m；实测所得最大侧向变形基本位于本文预测范围0.094～0.147 m 的中间位置，论证了本文方法的有效性。笔者针对试验路堤B的分析结果同样表明：本文方法计算所得的排水板地基沉降-时间曲线及路堤坡脚处的最大侧向变形均与实测数据吻合较好，限于篇幅，不赘述。

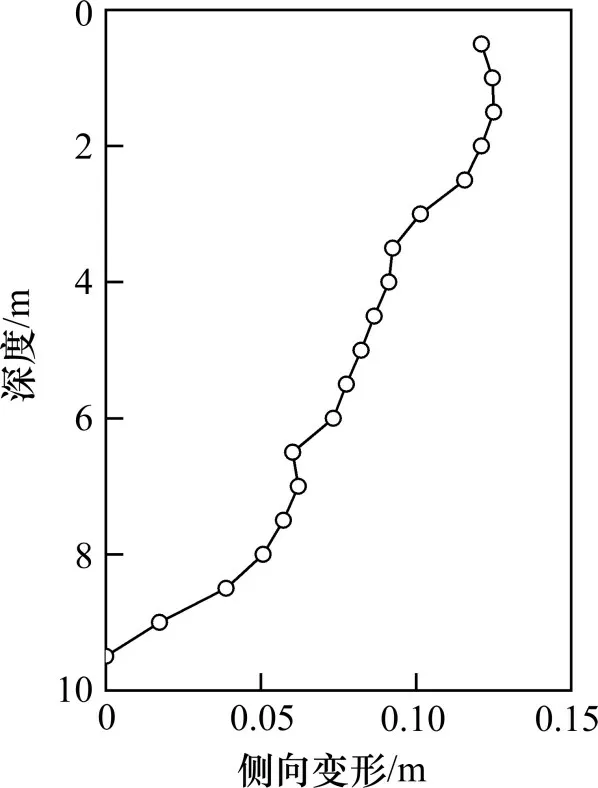
图9 试验路堤A侧向变形实测曲线Fig.9 Measured lateral deformation of embankment A

6 结论

1) 针对塑料排水板地基表层的双向排水固结效应，提出了该双向排水固结层厚度Hd的近似计算方法。分析表明：Hd的值主要与竖向排水相对于水平向排水的效应大小有关，且Hd随圆柱体排水单元体直径De，排水板涂抹区直径ds以及原状土体水平渗透率kh与涂抹区水平渗透率ks之比的增加而非线性增大。

2) 综合地基表层的双向排水固结效应及堆载预压荷载的时变特性，提出了阶梯型等效时变荷载下排水板地基固结度的计算方法。分析结果表明：阶梯型荷载等效法计算排水板地基固结度的加载步划分步数不宜小于4步，此时本文方法与有限元仿真计算总体吻合较好，最大误差少于10%，特别当模型地基的固结度U超过50%时，本文方法与有限元计算结果基本一致(误差在5%以内)，验证了本文方法的适用性。

3) 结合提出的排水板地基固结度计算方法及地基土的压缩特性，建立了预压荷载下排水板地基沉降-时间曲线的实用分析法，并将上述方法推广应用于排水板地基最大侧向变形的预测计算，综合形成了排水板地基变形计算的简易法。

4) 基于典型试验段路堤的应用分析表明，本文方法计算所得排水板地基的最终沉降值为0.531 m，接近0.541 m 的实测值，且实测地基最大侧向变形(0.125 m)基本位于本文预测范围0.094～0.147 m 的中间位置，此外本文方法计算所得的排水板地基沉降-时间曲线与实测沉降曲线的吻合度也较高，论证了本文方法的有效性和适用性。