涡轮集气腔结构参数优化研究

王振宇，王春华，张靖周,2

(1. 南京航空航天大学能源与动力学院江苏省航空动力系统重点实验室，江苏 南京，210016；2. 先进航空发动机协同创新中心，北京，100191)

为了提高航空燃气涡轮发动机的循环效率，人们不断增大压气机的增压比和涡轮进口燃气温度，高温部件的工作环境愈发恶劣[1]。为了保证涡轮发动机工作环境的安全，人们对发动机冷却系统的性能提出了更高的要求[2]。

涡轮集气腔承担着为导向叶片输送冷气的任务，是航空发动机空气系统的重要组成部分[3]。集气腔流动损失直接影响发动机工作效率；而出流分配的不均匀则会导致部分叶片冷气流量不足或是冷气流量过大，对下游热端部件冷却造成不利影响[4]。

传统涡轮集气腔由于冷却气进气直接冲击腔室内壁面，会形成明显的出流流量分配不均现象。赵曙[5]通过相似原理以航空发动机集气腔的1/4 部分为研究对象，对其内部流动特性进行了实验研究，发现在不同雷诺数下集气腔腔室内部压力分布规律和出口质量流量分布规律基本相同，正对进口的区域静压系数较小，离入口较远的出口处流量较小。姚甜等[6]通过实验发现传统集气腔分流规律并不均衡，正对主进气口的出流孔流量最大，紧邻其两侧的周向出流孔流量明显减少。集气腔的总流量会随着腔室高度和进出口压比的增大而升高，但是这2个参数的改变都不会影响出流分布规律。张小颖[7]将CFD模拟与实验相结合，详细研究了集气腔的各个结构参数如进口直径、出流孔直径、进出口轴向间距等对集气腔分流特性的影响，其结果表明当进口总压一定时，集气腔的几何参数可在一定程度影响了集气腔出流孔的出流不均匀度。

集气腔流量分配特性明显受到几何结构参数和来流热力参数的影响[8]，故研究集气腔结构参数的优化方法具有重要的意义。LEE[9]采用单目标优化代理模型，以气膜冷却效率为优化目标，对平板表面扇形孔结构进行了优化，并采用多目标优化代理模型，以气膜冷却和气动损失为目标函数，对扇形孔结构进行了优化。黄莺等[10]对涡轮叶片吸力面特性位置的扇形气膜孔结构进行优化，针对扇形气膜孔的多个结构参数，通过径向基神经网络构建代理模型，采用遗传算法搜索最优设计点，得到冷却效率更好的优化结构。WANG 等[11]针对多孔层板结构，从给定的几何变量范围出发，采用径向基神经网络和遗传算法相结合的方式进行结构优化，优化后多孔层板结构的整体冷却效率提高，压降降低，其热力学性能大大提升。

为进一步降低集气腔内气流的流动损失，改善出流不均匀度，本文以进气导管直径、进出口轴向间距、进气导管倾斜角和出流孔周向偏角为设计参数，提出基于径向基函数(radial basis function，RBF)神经网络代理模型和遗传算法(genetic algorithm，GA)的集气腔结构优化方法；对优化效果进行测试，比较分析优化前后集气腔流动特征的差异。

1 物理模型和优化方法

1.1 物理模型

集气腔简化模型如图1所示，其计算区域由进气导管、腔室和出流孔排组成。冷却气体经过进气导管流入腔室之后从内壁面密集的出流孔流出。集气腔基准结构参数如下：进气导管A1～A4 直径(D)为30 mm，腔室高度(h)为20 mm，腔室下端直径(Dd)为866 mm，上端直径(Du)为821 mm，集气腔整体高度为262 mm，40 个出流孔H1～H40 均匀排布在腔室内壁，直径为10 mm。

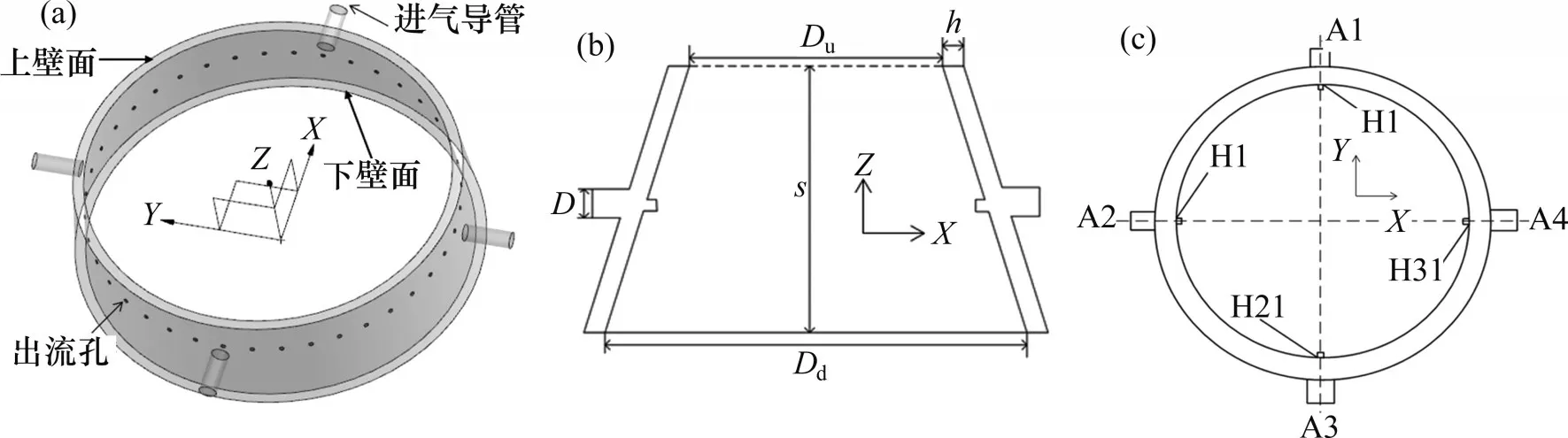
图1 集气腔简化模型Fig.1 Simplified models of coolant-collecting plenum

为进一步提高集气腔出流均匀度，降低流动阻力，在基准结构上引入进出口轴向偏差、进气导管倾斜度及出流孔周向偏差等参数，并选取进气导管直径、进出口轴向间距、进气导管倾斜角和出流孔周向偏角作为优化变量(见图2)。优化变量设计区间见表1。

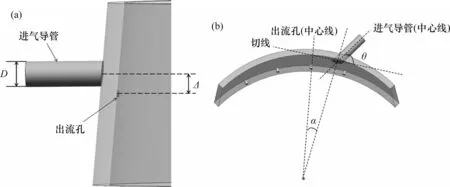
图2 优化变量示意图Fig.2 Diagram of optimization variables

表1 优化变量设计区间Table 1 Design range of optimization variables

流量不均匀度(σ)可以直观地反映集气腔出流孔的流量分布均匀性，定义σ为

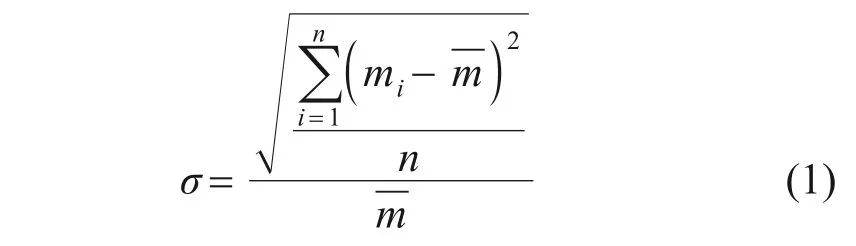
式中：m为出流孔的质量流量；n为出流孔总个数；i为出流孔序号；ˉm为出流孔平均质量流量。

流量系数(Cd)可以定量评价集气腔腔室内部的冷气流动阻力，其表达式为

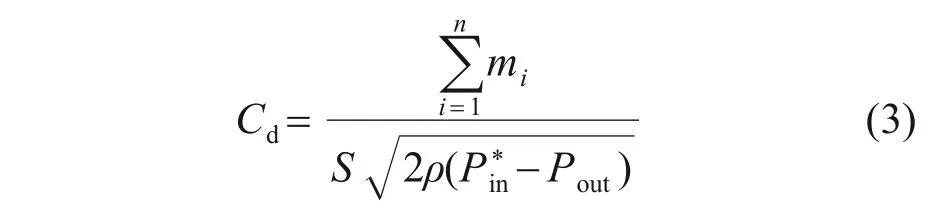
式中：S为出流面积；P*

in为进口总压；Pout为出口静压；ρ为气流密度；流量系数越大说明流动阻力越小。

1.2 优化方法

1.2.1 基本流程

优化过程以提升流量系数、降低不均匀度为优化目标，针对进气导管直径、进出口轴向间距、进气导管倾斜角和出流孔周向偏角展开优化，建立的目标函数为：

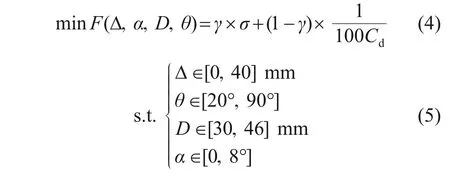
式中：指标权重γ∈[0，1]。

图3所示为优化基本流程。首先，通过拉丁超立方抽样方法进行数值实验设计，并进行CFD 求解，获得数据样本；其次，建立RBF 神经网络代理模型，并基于数据样本对代理模型进行训练；最后，引入遗传算法对优化变量进行全局寻优，分别以“最大化流量系数”“最小化出流不均匀度”“兼顾流量系数和出流不均匀度”为目标进行集气腔结构的优化。

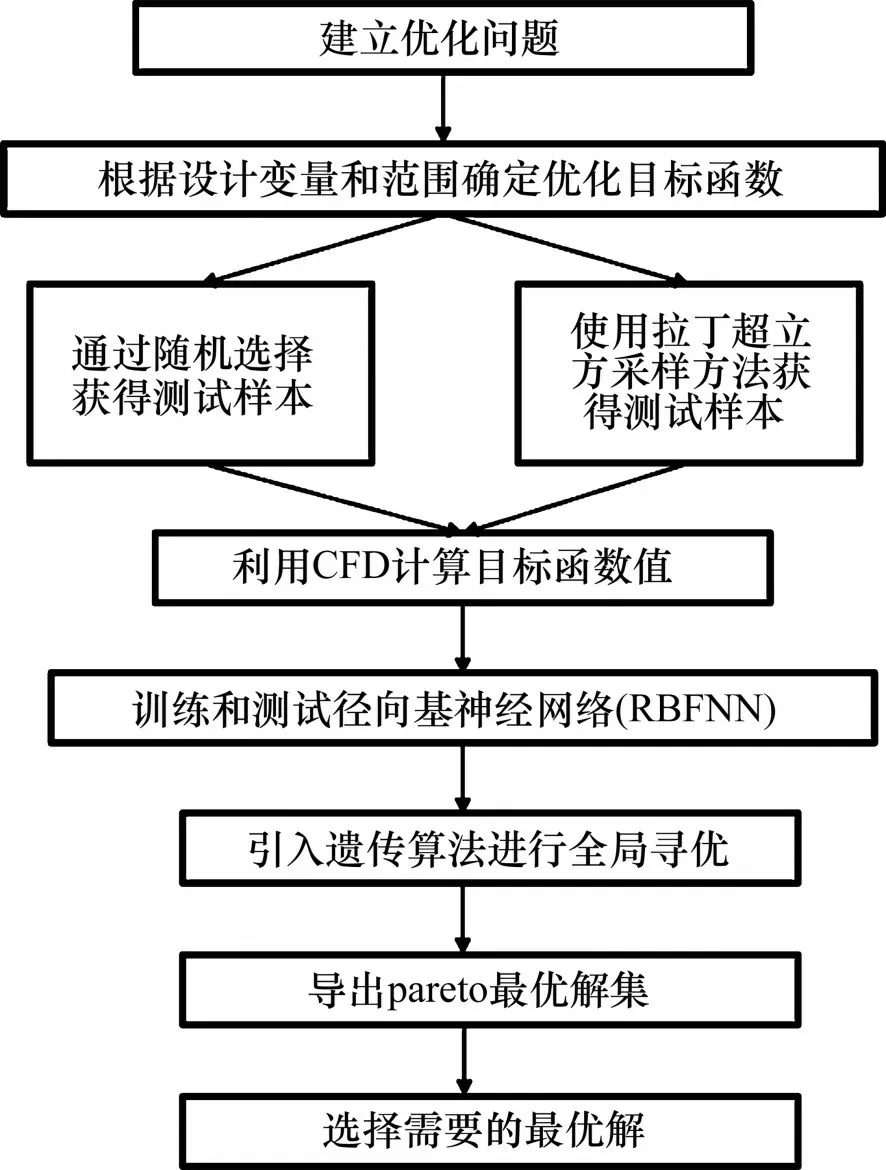
图3 优化基本流程图Fig.3 Basic flow chart of optimization

1.2.2 数值计算及验证

1) 数值计算。 拉丁超立方抽样(Latin hypercube sampling，LHS)是一种从多元参数分布中近似随机抽样的方法，属于分层抽样技术，优点在于可以保证覆盖每一个变量范围。本文通过LHS共得到60组数据样本，其中48组为RBF神经网络训练样本，12组为RBF神经网络测试样本。

使用ICEM软件对计算模型进行非结构网格划分。在进口孔与出流孔以及壁面附近进行局部网格加密，为了满足增强型壁面函数对近壁区域网格的要求，在壁面附近设置边界层网格，使量纲一参数y+≈1。网格数量通过网格独立性测试予以确定，如图4 所示，基准结构计算网格为445 212 3个。

图4 计算网格示例图Fig.4 Example of computational grids

使用Ansys Fluent 软件对数据样本进行求解，集气腔进口气流Ma＜0.3，所以，气体域可以作为不可压理想气体处理。集气腔边界条件设计如下：外环导管进气采用压力入口(pressure-inlet)，=1.2 MPa，=700 K，出流孔采用压力出口，Pout=1.06 MPa，其余壁面均设置为绝热，无滑移壁面。

蒋亮等[12]通过CFD模拟与实验相结合的方法，发现Realizablek-ε湍流模型在集气腔计算中具有较高的计算精度，因此，本文也使用Realizablek-ε模型。动量、湍流动能、耗散率和能量以及离散方程均采用二阶迎风格式，压力速度耦合采用SIMPLEC算法；解的收敛标准为残差小于10-5。

2)实验验证。实验装置如图5所示，该装置由供气系统、测量系统和实验件3个部分组成。实验装置由单螺杆压缩机供气，额定体积流量为37 m3/min，压气机提供的气源通过涡街流量计进行监控(流量计型号为LU-13021BD0211010，量程为5～50 m3/min，精度等级为1.0)。气流通过转接头后分成四路，使用阀门调节进气导管的流量以达到流量平衡，气流从4 个进气导管流入集气腔，最终从实验件内壁出流孔流出。实验中使用热球风速仪逐一测量每个出流孔的出流平均速度(热球风速仪型号ST-732，分辨率为0.01 m/s)。经过计算得到每个出流孔的质量流量。

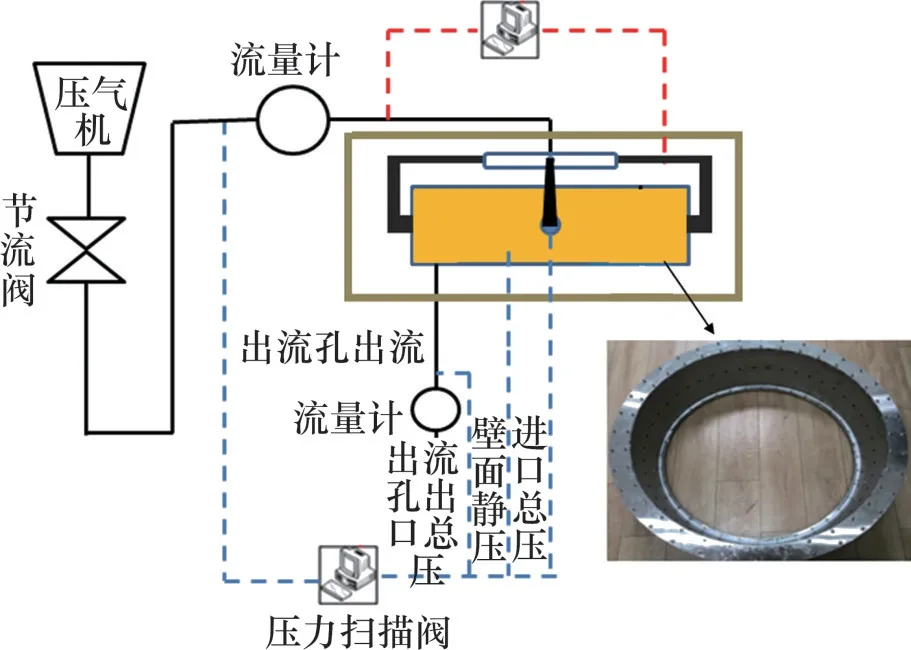
图5 实验装置Fig.5 Experimental setup

当入口流量为0.2 kg/s 时，出流孔质量流量实验结果与计算结果对比见图6，两者相对误差为7.6%。由于受实验设备加工精度、测量仪器、人员因素和实验室环境等综合因素的影响，实验与计算结果存在偏差，但相对误差在合理范围内，说明CFD模型整体上具有较高的计算精度。

图6 出口质量流量实验与计算结果对比Fig.6 Comparison between experimental and calculated results of outlet mass flow

1.2.3 代理模型

RBF 神经网络是一种性能优良的前馈型神经网络[13]，可以以任意精度逼近任意的非线性函数，可用于构建代理模型。RBF 神经网络拓扑结构结构分为输入层、隐藏层和输出层[14]，如图7 所示。隐藏层第i个神经节点的输入值Hi为

图7 RBF神经网络拓扑结构Fig.7 Topologic structure of RBF neural network

式中：X=(x1，x2，…，xm)，为RBF 神经网络的输入向量；Ti=(t1i，t2i，…，tmi)，为第i个神经节点中心向量。

隐藏层第i个神经节点的输出值φj可表示为

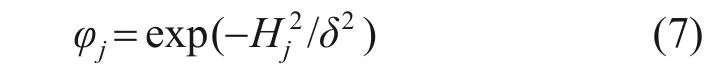
式中：δ为扩展速度。

RBF神经网络的输出值可以表示为

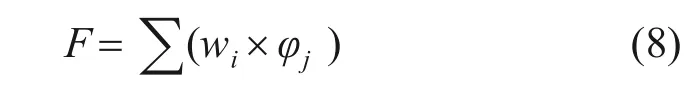
式中：w=(w1，w2，…，wn)，为隐藏层和输出层之间的连接权重[12]。

通过Matlab 神经网络工具箱实现RBF 神经网络的构建，其预测性能受扩展速度δ影响[15]。本文采用试错法确定δ。图8所示为RBF神经网络预测结果和测试样本结果(CFD 计算结果)对比。由图8可见流量系数Cd的RBF预测值和CFD计算值的平均相对误差为6.4%，出口流量不均匀度σ的RBF预测值和CFD 计算值的平均相对误差为2.8%。RBF 神经网络扩散速度通过试错法来确定，对于流量系数，最优的扩展速度为0.76，对于出流不均匀度，最优的扩展速度为0.54。

图8 不同参数RBF预测值与CFD计算值对比Fig.8 Comparison between the predicted values from RBF neural network and CFD calculated values of different parameters

1.2.4 遗传算法优化

遗传算法是一种可以模拟自然界进化过程的优化算法[16]，该算法通过对待解决问题的所有可能解集进行随机搜索，从而找到全局最优解[17]，具有适应范围较广、全局搜索能力较强的特点。

在遗传算法优化迭代过程中，相对适应度由个体适应度在群体总适应度所占的比例决定；变异参数通过高斯变异函数确定，交叉参数通过分散交叉函数确定[18]。交叉概率Ptc和变异概率Ptm与进化代数的关系分别为：

式中：t为进化代数；tmax为最大进化代数，l=10。

通过Matlab 遗传优化工具箱来实现遗传算法优化，并在工具箱内对以下参数进行设置：种群为60；选择高斯函数作为变异函数[19]；选择中间比率为1 的交叉函数；设置前向型进化且步长为0.2，最大迭代步长为200。

根据遗传算法，以提高出口流量系数和减小出流不均匀度为目标寻求多目标优化的Pareto前缘解集，得到一条非线性曲线，如图9所示。对优化目标赋予权重以区分优化结果的性能差别，用来满足实际生产中所需要的特性要求。M1和M2均为极值点，M1代表最大出口流量系数极值点，此时，最大流量系数目标权重为1；M2代表最小出流不均匀度极值点，此时，最小出流不均匀度目标权重为1。针对优化目标分别定义权重为(1，0)和(0，1)。中间值为M3点，此处权重为(0.5，0.5)。表2 所示为不同流量系数权重下的多目标优化结果。

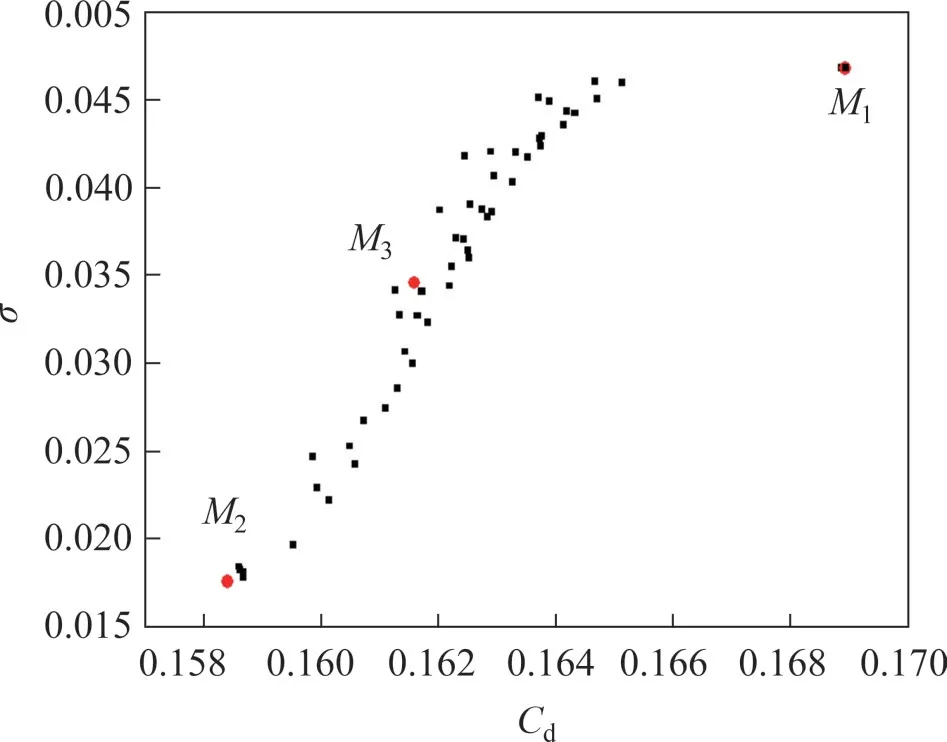
图9 Pareto解集Fig.9 Pareto solution set

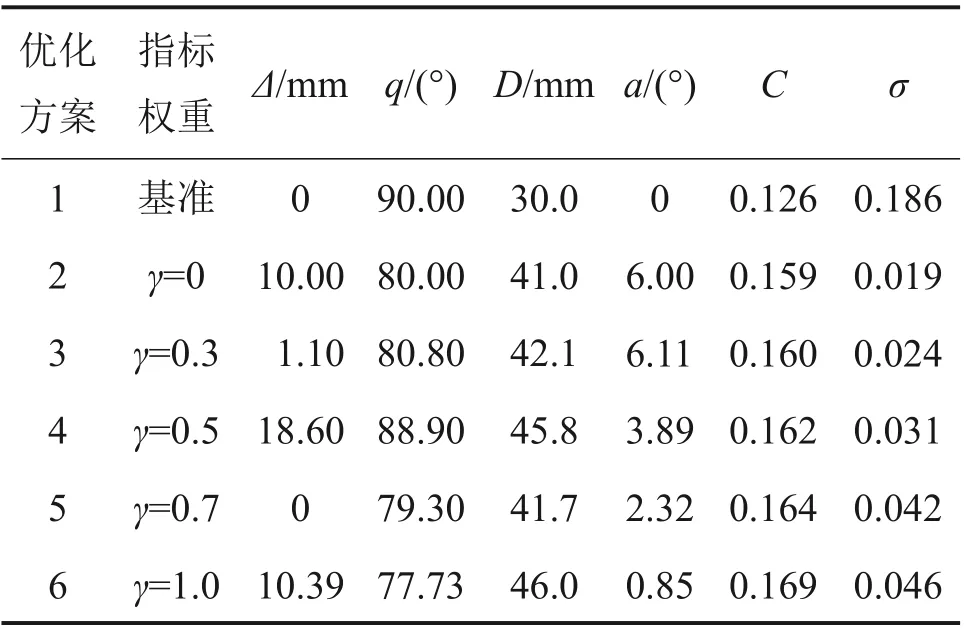
表2 不同流量系数权重下的优化结果Table 2 Optimization results of flow coefficient with different index weights

2 优化结果分析

2.1 单目标优化结果分析

当入口流量为0.2 kg/s 时不同优化方案中优化前后出流孔流量分布如图10 所示。图10 中，A 组为涡轮集气腔基准结构出流孔排流量分布，B组为以最大流量系数为优化目标(即表2 中优化方案6)所得优化结果，C组为以最小出流不均匀度为优化目标(即表2 中优化方案2)所得优化结果。由图10可见：优化后，B 组整体流量相对于A 组明显升高，总流量提升30%，集气腔输送冷气能力明显提高；出流不均度降低76%，冷气分配更加均匀。B 组存在3 个流量极大值点，4 个极小值点，相比于优化前，出口流量极大值点减小，在一定程度上可以避免冷气浪费；出口流量极小值点明显增大，可防止出现冷气不足现象。优化后，C组整体流量相对于A组提升26%，总流量提升的同时，出流孔流量分布曲线中未出现差距过大的极大值和极小值点，出流不均匀度减小90%，极大地优化了出流孔排流量分布规律。

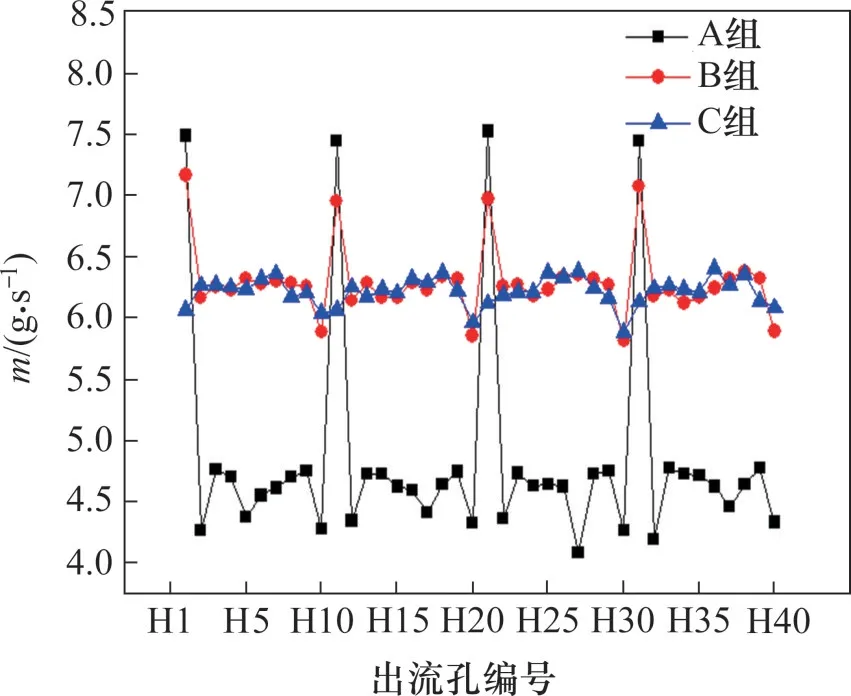
图10 优化前后出流孔排质量流量分布Fig.10 Outlet mass flow distributions before and after optimization

图11 所示为初始模型基准结构的腔室内部流场和压力分布云图，初始模型中进气导管直径为30 mm，气流从进气导管垂直入射集气腔腔室。H1 出流孔正对进气导管，来流动压被充分利用，部分高速气流未碰撞腔室内壁而是直接冲击流入出流孔。H2 和H40 出流孔位于壁面流动区域，高速气流冲击壁面后，动压转变为静压，在出流孔H1 出流孔两侧形成了明显的高压带，气流流动方向从垂直壁面转变为平行于出流孔排的贴壁流动。只有很少一部分气流从H2 和H40 等出口流出。因此，H2和H40的出流流量明显比H1的小。在2个进气孔中间区域，来自两侧进气孔的高速壁面流发生相向碰撞，能量损失和总压降低，使得出流能力降低，出现极小值。这将导致冷气不足。

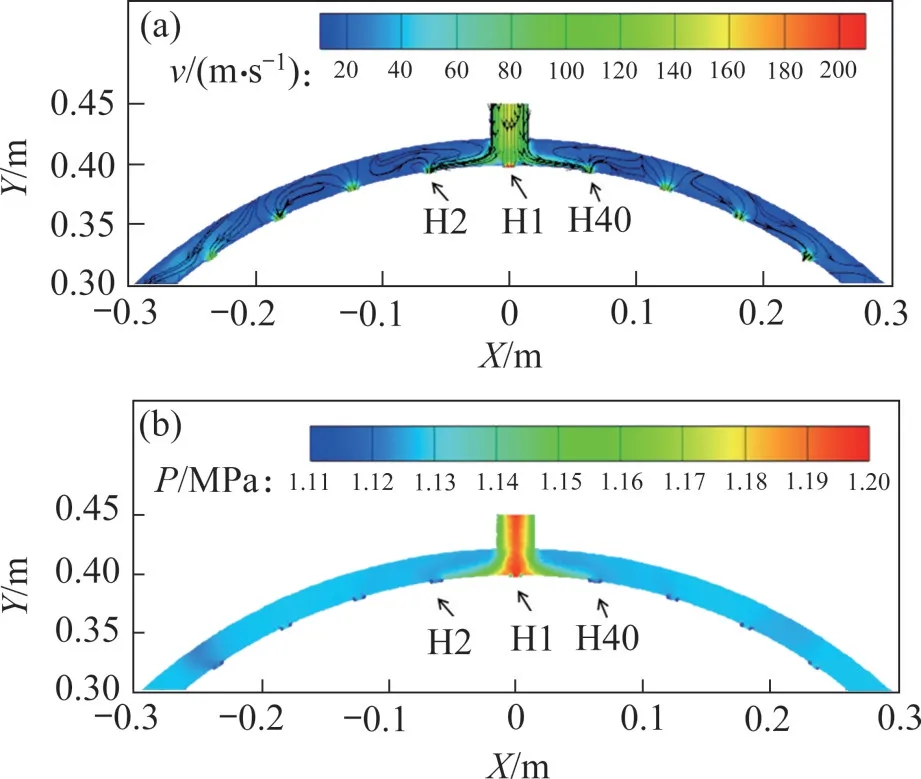
图11 基准结构流场和压力分布Fig.11 Flow field and pressure distribution in the benchmark structure

优化后，B组结构进气导管直径为46 mm，进气导管倾斜角为77.73°。图12 所示为优化后B 组腔室内部流场和压力分布云图。由图12 可知：在相同进出口压比下，增大进气导管直径可以减小进气导管内部压力。由流线分布结果可知：倾斜的进气导管可以防止气流垂直入射，只有少部分冷气未冲击腔室内壁面，直接流入出流孔H1，所以，B 组H1 出流孔流量比A 组的小，斜向进气使更多的气流转变为壁面流动，从而H1两侧的多个出流孔流量相对于原始结构明显增大。倾斜进口同样可以使气流转变为壁面流动过程中的流动损失更小。

图12 B组结构流场和压力分布(γ=1)Fig.12 Flow field and pressure distribution in Structure B with γ=1

优化后C 组集气腔进气导管倾斜角为80°，周向偏角为6°。图13 所示为C 组结构内部流场和压力场。由于周向偏角的存在，正对进气导管的位置没有出流孔，可避免出现出流流量极大值。来自进口的冷气高速冲击集气腔内侧壁面，腔室内壁面形成明显的高压带，在压力梯度的作用下，气体与壁面碰撞后由轴向流动转变为壁面流动，沿腔室内壁逐一从出流孔流出集气腔，出流孔流量沿着气流流动方向逐渐减小，在2个进气导管的中间区域与反方向来流相撞，共同流出集气腔。因此，在C组集气腔结构中出现没有明显的出流流量极大值和极小值，出流孔排流量分布均匀，相比原始结构，出流不均匀度下降了90%。

图13 C组结构流场和压力分布(γ=0)Fig.13 Flow field and pressure distribution in Structure C with γ=0

2.2 多目标优化结果分析

对原始集气腔结构进行多目标优化，入口流量为0.25 kg/s时不同流量系数权重下多目标优化结构出流孔排质量流量分布如图14所示。

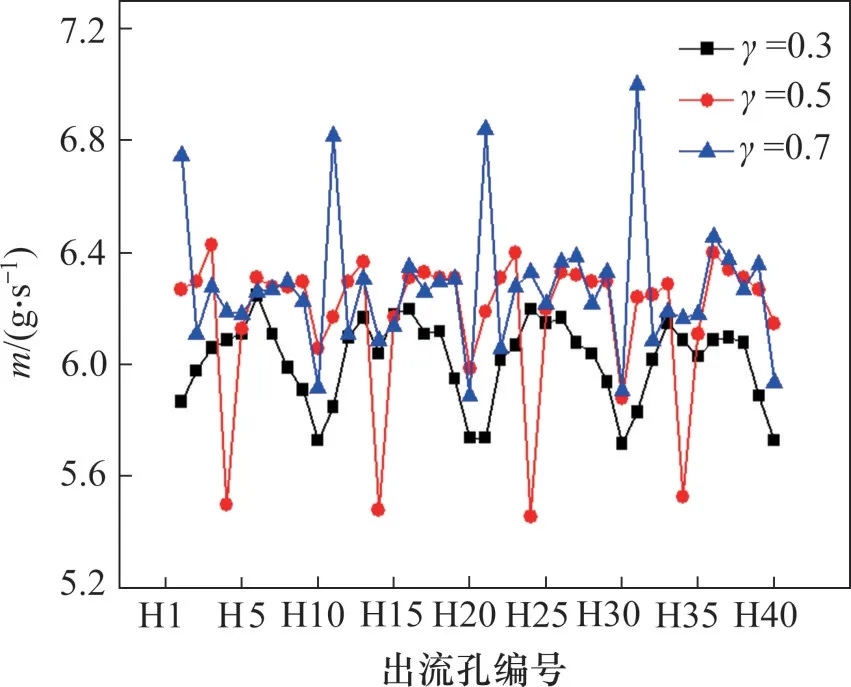
图14 多目标优化后结构的质量流量分布Fig.14 Outlet mass flow distributions after multiobjective optimizations with different γ

以流量系数权重为0.5时的优化结果为例，分析腔室内部流场和压力分布，结果如图15 所示。由图15 可见：优化后，进气导管直径为45.8 mm，进气量明显增大，周向偏角为3.89°，没有正对进气导管的出流孔，避免出现出流流量极大值。进口气流直接冲击腔室内壁面，在H1 和H40 出流孔的周围形成复杂的涡。由于压力梯度的作用，气流转变为壁面流动，沿两侧壁面逐一从出流孔流出腔室。优化后轴向间距为18.6 mm，由腔室截面流场分布可以看出，增大进出口轴向间距同样可以减小正对出流孔的流量，减小出流不均匀度。进气导管的细微倾角间接导致只有很少的气流能够到达2个进气导管中间位置的出流孔，所以，该位置压力较低，对应流量曲线中的极小值点。

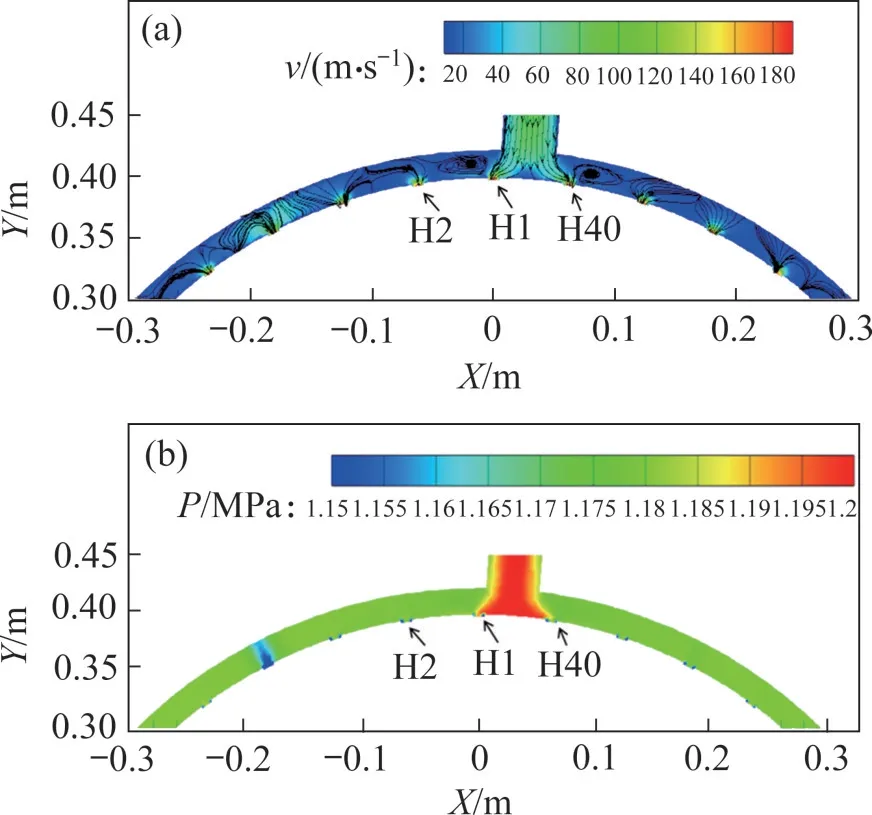
图15 优化结构流场和压力分布(γ=0.5)Fig.15 Flow field and pressure distribution in the optimized structure with γ=0.5

由上述分析可以看出：进口直径、进口偏角、进出口轴向间距和出流孔周向偏角4个结构参数共同影响腔室内部流动特性，在不同流量系数权重下的优化结果没有呈现明显的数值规律。整体而言，在同一工况下，增大进气导管直径可以有效地提高出流孔流量系数；增大倾斜角可以增大入射气流切向速度，减小流动损失和出流不均匀度；进出口轴向间距和周向偏角的存在避免了气流未碰撞腔室内壁直接流出腔室(轴向间距影响如图16所示)，出流不均匀度显著减小。

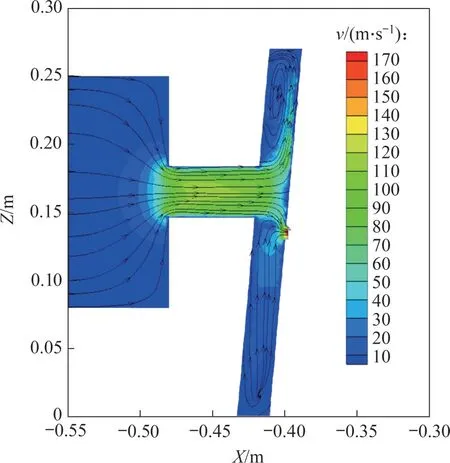
图16 流场分布侧视图Fig.16 Side view of flow field distribution

3 结论

1)提出了一种耦合神经网络模型和遗传算法的涡轮集气腔结构优化方法。首先，通过拉丁超立方抽样方法进行数值实验设计，并进行CFD 求解，获得数据样本；其次，建立RBF 神经网络代理模型，并基于数据样本对代理模型进行参数训练；最后引入遗传算法对优化变量进行全局寻优。

2) 当以最大出流孔流量系数为优化目标时，最优结构参数如下：轴向间距为10.39 mm，进气导管倾斜角为77.73°，进气导管直径为46 mm，周向偏角为0.85°。当以最小出流不均匀度为优化目标时，最优的结构参数如下：轴向间距为10 mm，进气导管倾斜角为80°，进气导管直径为41 mm，周向偏角为6°。

3)以最大化流量系数和最小化出流不均匀度权重分配均为0.5为目标，针对涡轮集气腔结构展开多目标优化。结果表明，优化后腔内流线变化更为平缓，进气导管射流冲击效应和出流孔的抽吸效应明显减弱。