波浪形前缘叶片对动车组牵引变压器冷却风机气动性能及噪声特性的影响

冀怡名，史佳伟，圣小珍，何远鹏，徐凡，陈力

(1. 西南交通大学牵引动力国家重点实验室，四川 成都，610031；2. 上海工程技术大学城市轨道交通学院，上海，201620；3. 同济大学上海地面交通工具风洞中心，上海，201804)

“十四五”规划将推动更高速度动车组的研发，列车运行速度的提高意味着动车组上的牵引变压器、牵引电机等设备需要以更高的负荷运行。这些设备运行时会产生大量的热，如果这些热量无法及时散去，就很可能损坏本身及周围的设备，影响列车运行的安全性[1]，为此，需要对发热设备进行散热处理。其中，动车组牵引变压器的散热一般通过安装在车体下方的冷却风机来实现，但高速旋转的风机在发挥其冷却作用的同时会产生很大的噪声，因此，为了提升高速列车的NVH(noise, vibration, harshness)性能，有必要对牵引变压器冷却风机的噪声进行控制。

动车组牵引变压器冷却风机属于轴流风机，其噪声来源主要为气动噪声。近年来，仿生学的发展为降低风机的气动噪声提供了新的思路，常见的基于仿生学原理设计的降噪叶片有仿鸮类翅膀翼形的叶片[2]、仿猫头鹰翅膀的锯齿形叶片[3]及仿鸟类翅膀尖部的叶尖小翼结构[4]等。此外，驼背鲸鳍肢前缘的波浪形结构具有较好的动力学性能和降噪特性[5-6]，因此，基于驼背鲸鳍肢前缘凸起的波浪形结构的仿生设计也得到了国内外研究人员广泛关注。

FISH 等[7]对驼背鲸鳍肢前缘结构进行了研究，由于驼背鲸灵活的机动性和其庞大身躯的不匹配性，于是他们测量并绘制了不同的鳍肢截面形状，通过风洞实验研究了鳍肢凸起结构的流体动力学性能，发现鳍肢凸起结构可提升大迎角下翼型的升力，并延缓失速。此后，人们对波浪形结构形叶片的气动特性和噪声特性进行了大量研究。MATHEWS等[8]对湍流翼型上的波浪形前缘结构的降噪机理进行了理论分析，并提出了波浪形前缘降低平板噪声的理论模型；NARAYANAN 等[9]采取实验的方法研究了前缘锯齿形对平板翼型宽频噪声的影响，发现锯齿的幅值对噪声的影响较大，波长对噪声的影响较小；CORSINI 等[10]研究了正弦形波浪前缘的三维风扇叶片的流动机理，结果表明，正弦型前缘提高了风扇失速后的升力恢复，在一定程度上还可以提高风扇的效率；张照煌等[11]通过图像处理技术获取了座头鲸胸鳍外形特征，并对比了座头鲸胸鳍外形翼型与常规翼型的空气动力学性能，发现座头鲸胸鳍外形翼型的升力系数和升阻比比常规翼型的高；程颢颐等[12]研究了翼型常规尾缘、波浪形前缘、锯齿形尾缘的气动噪声，发现波浪形前缘主要降低低频段的噪声，波浪形的波长越短，降噪效果越明显。

综上所述，目前对于波浪形前缘的研究大多集中于翼型设计上，对于将波浪形前缘结构应用于风机叶片的研究还较少，具有波浪形前缘结构的叶片对动车组用轴流风机气动性能和气动噪声特性的影响尚不明确。

基于此，本文作者以某型动车组牵引变压器冷却风机为研究对象，采取仿驼背鲸鳍肢前缘凸起的波浪形结构对其出风口叶片进行改形，设计3款不同的叶片前缘，通过数值模拟研究波浪形前缘叶片对牵引变压器冷却风机气动性能和气动噪声特性的影响，为波浪形前缘叶片在动车组冷却风机上的工程应用提供参考。

1 原型风机模型及波浪形结构参数

图1(a)所示为某公司设计和生产的动车组用轴流冷却风机的实物图，为了减小计算资源，在不影响计算精度的条件下，利用3D 模型设计软件UG对该风机的电机、支座、螺栓、圆角等进行简化处理，简化模型如图1(b)所示。表1所示为该风机的结构参数。

图1 动车组轴流冷却风机模型Fig.1 Model of axial cooling fan for EMU

表1 冷却风机结构参数Table 1 Structural parameters of cooling fan

由文献[13]知，要降低动车组轴流冷却风机的噪声，应当优先考虑出风口叶轮；张照煌等[11]指出，驼背鲸鳍肢前缘凸起结构可拟合为正弦曲线。基于以上2点，参照下式对冷却风机的出风口叶轮叶片前缘进行波浪形结构改形：

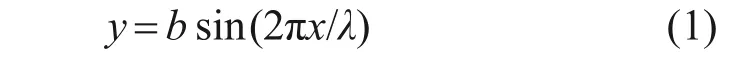
式中：b为振幅，mm；λ为波长，mm。

共设计了3款叶片，如图2所示。表2所示为3款波浪形前缘叶片的参数。

图2 仿驼背鲸鳍肢前缘凸起的波浪形结构叶片模型Fig.2 Wave structure blade model of humpback whale fin front protruding

表2 波浪形前缘叶片设计参数Table 2 Design parameters of wavy leading edge blades

2 数值模拟方法及验证

2.1 计算域及网格划分

将冷却风机的出风口和进风口区域延伸成长直管道，以作为流体计算域，延伸长度分别为叶轮直径的3倍和叶轮直径的4倍，此时将计算域分为进口、风机、出口3个区域，如图3所示。

图3 冷却风机数值计算域Fig.3 Numerical calculation space of cooling fan

数值计算前需要对风机流场的计算域进行离散处理，利用STAR-CCM+软件对3 个区域网格进行划分，网格类型为切割体网格，这样可以在绝大部分区域生成正交性很好的六面体网格，利用较少的网格，实现与非结构化网格等同的计算精度。为了实现相邻区域界面之间的数据传递，还需要在各区域之间设置界面。本文作者还对动、静叶轮表面附近区域以及相邻壁面附近区域进行了网格加密处理，表面网格长度为2.5 mm，并在各个固体表面生成了12 层边界层网格，其中y=0截面的网格图如图4所示。

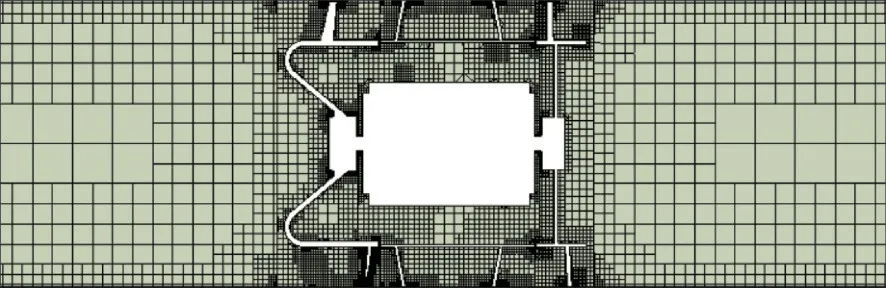
图4 y=0截面的网格分布Fig.4 Grid distribution of y=0 section

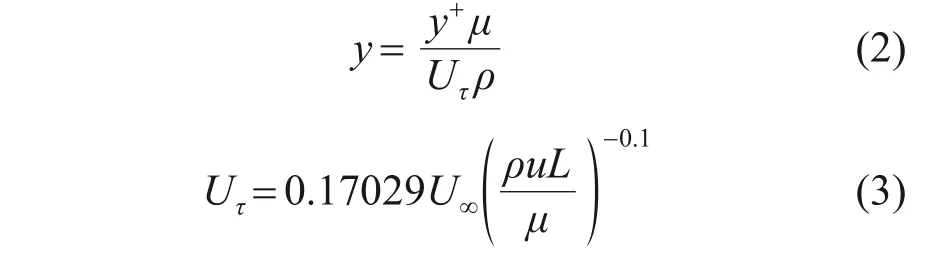
式中：y为第一层网格高度，m；y+为反映垂直于壁面湍流情况的量纲一参数；ρ为流体密度，kg/m3，取值1.225 kg/m3；μ为动力黏度，kg/(m·s)，本文取1.789 4×10-5kg/(m·s)；Uτ为估算速度，m/s；u为流动特征速度，m/s，取叶片旋转的最大速度，为43.70 m/s；L为特征长度，m，取叶轮的直径0.568 m；U∞为来流速度，m/s，取叶片旋转的最大速度43.70 m/s。

由式(2)计算得到第一层网格高度为0.01 mm，从而保证冷却风机表面的y+小于1，以达到大涡模拟和“紧致”声源对网格的要求[14]。

图5 所示为冷却风机的壁面y+，由图5 可以看到：壁面y+均小于1。同时，根据x和z方向的第一层网格高度估算壁面x+和z+，最大值分别为123.67和118.65，网格分辨率满足计算要求。

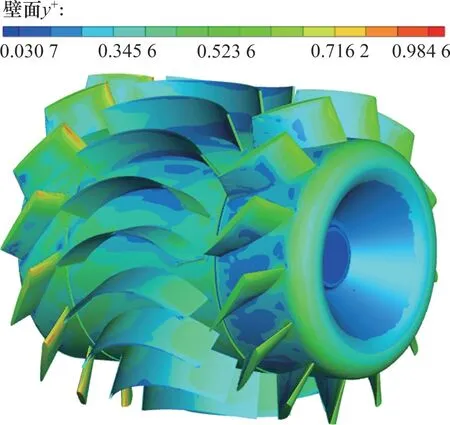
图5 冷却风机壁面y+Fig.5 y+of cooling fan wall

2.2 流场和声场的计算模型

利用商业软件Ansys Fluent对冷却风机的流场和气动噪声进行数值模拟，首先对其进行稳态计算，再将稳态的计算结果作为初始值进行瞬态计算，以加速收敛，减小计算时间。由于冷却风机的马赫数为0.13(小于0.2)，属于低速不可压流动，所以，选取压力基求解器进行求解；此外，冷却风机内部流动基本不会涉及流体温度的改变，故模拟时能量方程处于关闭状态。

以叶轮外径为特征长度，可得冷却风机的雷诺数为1.699 25×106，属于高雷诺数流动，稳态计算的湍流模型选择RNGk-ε模型。进口区的端面设置为压力进口边界，为1.01×105Pa，出口区的端面设置为压力出口边界，为1.01×105Pa。

在稳态计算中，动叶轮叶片表面设置为旋转壁面，其余表面设置为无滑移壁面边界。进风口叶轮和出风口叶轮的旋转区域采用多运动参考系模型(MRF)，设定其旋转轴的方向为(0，0，-1)，旋转速度为1 470 r/min。求解方法选择适用于稳态计算且稳定性较好的SIMPLEC 算法。由于网格是结构化网格和非结构化网格的组合，所以，梯度离散选择精度高和计算资源低的Least Squares Cell Based 方法；压力离散格式选择标准格式，动量、湍动能、湍流耗散方程均采取具有较小截断误差的二阶迎风格式，从而保证计算的精度。当设置残差值小于10-4时，计算便收敛。

瞬态计算的边界条件与稳态时的一致，进风口和出风口叶轮区域采取滑移网格方法实现旋转，旋转参数设置与稳态的参数相同。时间离散为二阶隐式，压力速度耦合采取适用于瞬态计算的PISO 算法，压力离散格式为二阶迎风格式，动量离散格式为有界中心差分格式。瞬态模拟采用基于Smagorinsky-Lilly 亚格子应力的大涡模拟(LES)模型。

通过监测冷却风机的流量来判断流场是否发展充分，待流场发展充分后开启声学计算，声学计算时间取0.6 s，时间步长为0.000 1 s[13]，最大内部迭代步数为20 步，根据奈奎斯特采样定理，经傅里叶变换可以得到的最大频率为5 000 Hz。将大涡模拟得到的叶片表面压力脉动作为声源激励，结合FW-H 方程计算得到在转轴上距离出风口1 m监测点(0，0，1.32)m处的声压时域信息，通过快速傅里叶变换得到冷却风机的噪声频谱。由于噪声的波长远比冷却风机的特征长度长，因此，可不考虑叶片之间以及叶片与机壳之间的反射、折射和衍射[15]。

2.3 数值计算模型验证

为验证数值计算模型的准确性，参照GB/T 2888—2008“风机和罗茨鼓风机噪声测量方法”[16]布置噪声测点，对冷却风机噪声进行试验，图6所示为现场试验。因为试验条件有限，无法在半消声室进行，本次试验在侧墙装有吸声板的厂房进行。风机距离侧墙的距离约为3 m。

图7所示为在转轴上距离出风口1 m测点处(图6中标出)的频谱对比图，从图7可以看出：冷却风机的A计权声压级随频率呈先增加后降低的趋势，测试结果与仿真结果整体一致性较好，噪声的声能量显著频段一致，但在一些频段处噪声存在差异，造成这种差异的原因有以下3点：1)受试验条件所限，实测噪声存在地面及其他方向的反射所产生的噪声；2)FW-H 方程仅考虑了偶极子噪声，并未考虑流动分离、湍流边界层、涡旋脱落产生的随机宽频带噪声；3)噪声预测模型未考虑风机内部的声反射对噪声的影响。

图6 现场试验示意图Fig.6 Diagram of field test

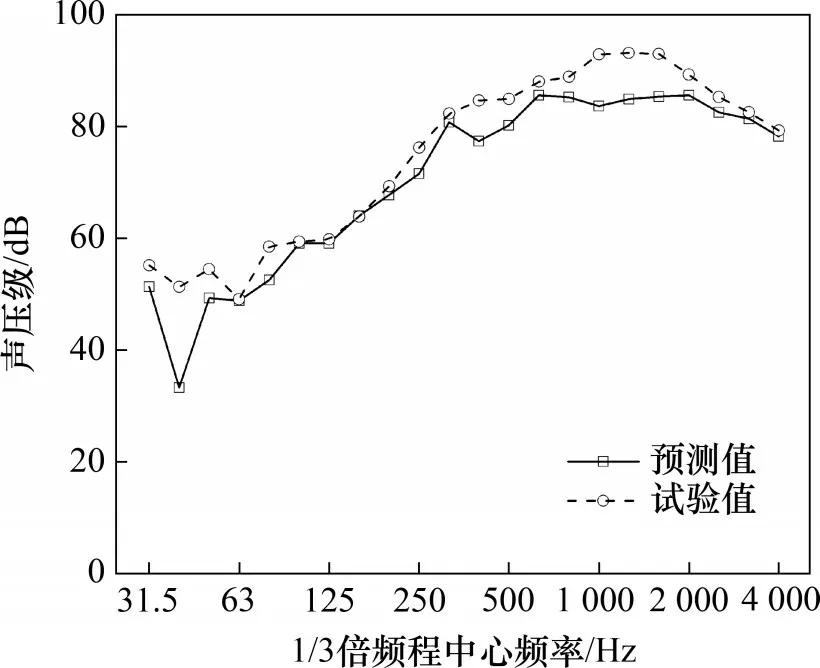
图7 试验与预测的噪声对比Fig.7 Comparison of noise between experiment and prediction

此外，该测点处的试验和预测采取A 计权的总声压级(0～5 000 Hz 范围内)分别为98.3 dB 和93.7 dB，两者差值为4.6 dB；风机试验和预测的流量分别为165.0 m3/h 和170.3 m3/h，相对误差为3.2%。

由以上分析可得，本文冷却风机的流场和声场预测模型与试验一致性较高，相对误差在允许范围内，可以指导工程应用。

3 冷却风机数值模拟结果及分析

3.1 波浪形前缘结构对冷却风机气动性能的影响

设计仿生叶片的目的是降低冷却风机的气动噪声，但降噪不能以降低风机的气动性能为代价，故本文首先研究仿生叶片对风机气动性能的影响。

表3所示为设计工况下4种模型气动性能(流量和冷却效率)的计算结果，由表3 可得：对冷却风机进行波浪形前缘结构改造后，风机的流量和效率有所提高，气动性能得到改善，这也与驼背鲸良好的气动性能一致；其次，随波浪形前缘结构波长减小，冷却风机的效率逐渐增大。

表3 仿生叶片的气动性能的计算结果Table 3 Calculation results of aerodynamic performance of bionic blade

3.2 波浪形前缘结构对冷却风机流场的影响

冷却风机的流场特征可在一定程度上表征其气动噪声特性，因此，本文首先对冷却风机的流场进行分析，主要研究4种模型叶片前缘的压力分布、涡结构分布以及叶顶泄漏涡的强度，明确波浪形前缘对冷却风机流场特征的影响。

图8所示为波浪形前缘叶片和原型叶片前缘处的压力分布，同时给出了叶片前缘压力的局部放大图。冷却风机的叶片并不是直立叶片，而是扭转了一定角度的扭转叶片，故气体流经叶片的分流线不与叶片前缘重合，从而导致叶片压力最大处并不出现在叶片前缘处，而是与前缘呈一定的角度分布。原型叶片的最大压力近似呈直线分布，而波浪形前缘叶片的最大压力近似沿直线间断性分布，在靠近波峰处出现间断，使叶片前缘处的压差变小。与原模型相比，流经前缘处的气流较稳定，不易引发涡旋，因此，波浪形前缘叶片具有较好的气动性能。

由图8可知：原型叶片在前缘处的压力梯度分布比较狭小，当气流经过时会造成很大的压力脉动，从而更容易产生由于压力脉动造成的气动噪声。波浪形前缘叶片的压力梯度分布比较均匀，压差平稳过渡，且随波浪形前缘结构波长减小(模型A 的波长＞B 的波长＞C 的波长)，压力梯度分布的均匀性更强，产生的气动噪声更小。

图8 叶片表面的压力分布Fig.8 Pressure distribution on blade surface

涡声理论揭示了气动噪声来源于涡结构的破碎和拉伸[17]，图8所示为冷却风机叶片前缘处利用Q准则等值面得到的涡结构，Q的定义为

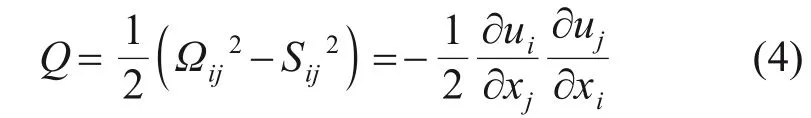
式中：Ωij和Sij分别为涡张量和应变率张量；ui和uj为速度张量；xi和xj为位移张量；Q为正值时表示该区域的流体涡的旋转作用比剪切作用大[18]。

图9 所示为Q=108s-2(该Q的涡结构等值面在前缘处较为明显)的等值面分布。由图9可以看到：4种模型在叶片前缘处的涡结构比较突出，原型风机的涡结构在前缘处呈连续均匀的条状分布，且涡的面积明显比其余模型的大；波浪形前缘结构的涡核分布呈现较强的不均匀性和不连续性，并具有一定的规律性：涡核分布在靠近波峰处出现间断，与其他部位相比，波谷处的涡结构比较突出。这是因为气流经过波浪形前缘的特殊结构时，来自两侧波峰的气流汇集到波谷处发生碰撞，造成气流在波谷处卷起形成涡核；对于叶片侧面的涡核分布，波浪形前缘结构叶片的涡较原模型的更小。

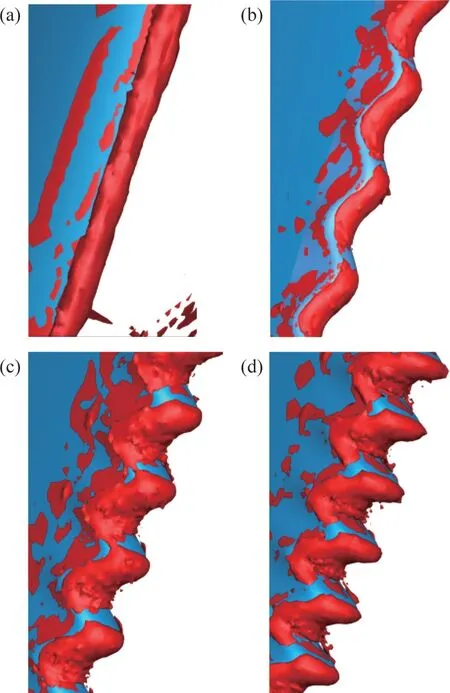
图9 冷却风机叶片前缘处Q=108 s-2的涡结构分布Fig.9 Vortex structure distribution of Q=108 s-2 at leading edge of cooling fan blade

以上分析表明，波浪形前缘结构可以破坏原模型涡核的分布状态，表现为波浪形前缘结构的波长越小(模型A 的波长＞B 的波长＞C 的波长)，破坏性越强，破碎形成的小涡越多。

由于叶片在叶顶(上、下游)两侧存在压差，故在叶顶处会形成泄漏流，随后泄露流在叶片低压一侧卷起形成泄漏涡。当泄漏涡向后扩散并脱落时，会引起较大的涡流噪声[19]。Q准则法只能确定涡的位置和分布，无法表征涡的强度，INOUE等[20]提供了研究叶顶泄漏涡强度和扩散路线的思路：叶顶泄漏涡的涡核处于一个低压区，这个低压区的压力均比周围区域的压力低，低压区的压力越低代表叶顶泄漏涡的强度越大，同时，叶顶泄漏涡沿等压线的波谷由低到高扩散和脱落。

图10所示为距离叶顶2 mm处的柱面内壁面的局部压力分布图，图中红色虚线表征叶顶泄漏涡的扩散路线。由图10可以看出：4种叶片模型低压区的压力由高到低依次为模型C、模型B、模型A、原模型。

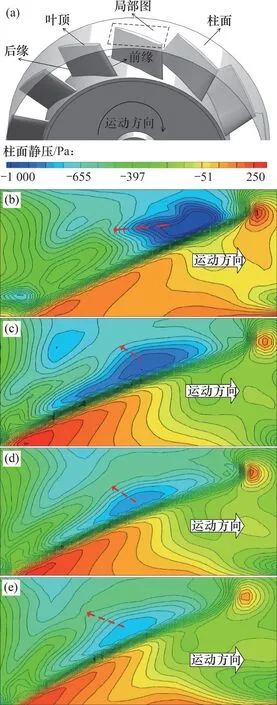
图10 距离叶顶2 mm处的柱面内壁面局部压力分布图Fig.10 Pressure distribution of cylinder 2 mm from blade tip

可以推断，波浪形前缘结构可以降低叶顶泄漏涡的强度，且随波浪形前缘结构波长的减小(模型A 的波长＞B 的波长＞C 的波长)，叶顶泄漏涡的强度降低。这也是波浪形前缘叶片提高轴流风机效率的一个重要原因：轴流风机的效率主要取决于流动损失，而二次流损失在流动损失中占据很大的比例，叶顶泄漏流是由于压差的作用而形成与主流方向不一致的流动，属于二次流范畴，波浪形前缘可以降低叶顶泄漏涡(二次流)的强度，因此，可以提高冷却风机的效率。

其次，还可以看到模型A，B和C的涡核中心相对于原模型向尾缘处偏移，这是因为波浪形前缘改变了叶片前缘的流动状态，随气流向尾缘处流动，涡核中心也发生了偏移。从图10 中的红色虚线可以看到：波浪形结构使叶顶泄漏涡的扩散路线远离尾缘，这样可避免泄漏涡与靠近尾缘的涡发生碰撞产生更加不稳定的流动。

3.3 波浪形前缘结构对冷却风机噪声的影响

通过瞬态计算得到距离出风口1 m处测点的声压级频谱图，再根据频谱图计算得到该测点处的总声压级。图11所示为4种模型噪声测点的A计权总声压级，由图11可见：模型A，B和C相对于原模型的降噪量分别为2.1，3.5和4.5 dB。

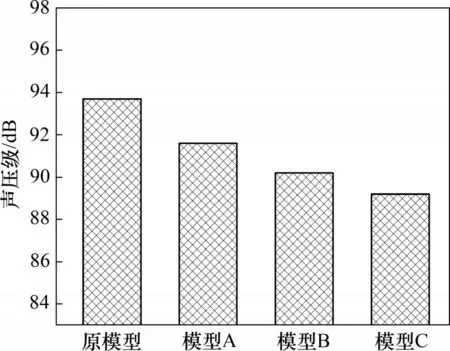
图11 测点(0，0，1.32)m处的A计权总声压级Fig.11 A weighted total sound pressure level at measuring point(0,0,1.32)m

由图11 可知：对出风口叶片前缘波浪形结构进行改造时，可以有效降低冷却风的气动噪声，且波浪形前缘结构的波长越小，降噪效果越好。考虑到实际加工的可行性以及计算资源的有限性，本文并未对更小波长的波浪形结构进行研究。

噪声主要是表面压力脉动产生的，一般用表面压力的变化率的偏导的均方根((∂P/∂t)RMS)表征压力脉动的强度，其定义为[21]

式中：N为采样个数；∂Pi/∂t为第i个采样点的压力变化率，Pa/s；t为时间，s；Pi为第i个采样点的压力，Pa。通过声压对时间的偏导的均方根可以确定声源位置及其强度。

图12 和图13 所示分别为4 种模型表面及其叶顶处的压力变化率的偏导均方根分布云图，图中红色箭头代表旋转方向，由图12 和图13 可以看到：出风口叶片的声源分布主要集中在叶片前缘、后缘、叶顶处。叶片前缘处的气流冲击、叶顶处的泄漏流以及叶片尾缘涡[19]的存在，使叶片局部产生不均匀流动，诱发了较大的压力脉动，因此，这些部分是主要的噪声源。其次，原模型在叶片前缘处和叶顶处的脉动强度最高，在波浪形前缘结构叶片模型中，随波长减小(模型A的波长＞B的波长＞C的波长)，叶片前缘处和叶顶处的压力脉动强度逐渐减小；波浪形结构还降低了尾缘处的脉动强度。

图12 出风口表面声压对时间偏导的均方根云图Fig.12 RMS of sound pressure on surface of air outlet

图13 叶顶表面声压对时间偏导的均方根云图Fig.13 RMS of sound pressure on tip surface of fan

结合3.1节的流场分析，波浪形前缘结构破坏了前缘处的涡结构，使前缘处的压力梯度相对原模型较均匀，因此具有更小的压力脉动强度；波浪形前缘结构还降低了叶顶处泄漏流的强度，改变了其扩散路径，从而使冷却风机叶顶附近的流动相对于原模型变得更稳定，最终降低了叶顶处的声源强度。对于波浪形结构降低了尾缘处的压力脉动强度，这是因为旋转作用的存在，使部分气流从上一个叶片前缘一侧直接作用在下一个叶片后缘一侧，波浪形前缘结构改善了前缘一侧的流动状态，间接影响了后缘一侧的流动，从而降低了后缘一侧的压力脉动强度。

下面分析波浪形前缘结构对冷却风机远场噪声的影响。为了避免谱泄漏对噪声信号频谱图的影响，将数值计算得到的远场噪声时域信号分3段后再对其进行加窗处理，此处的窗函数采取汉宁窗函数，重叠率为50%，然后对信号进行FFT变换得到噪声信号的频谱图。在原模型和波浪形前缘结构模型的频谱图中，超过2 500 Hz频段的声压级差别很小，因此，图14仅给出了0～2 500 Hz范围内噪声测点的A计权声压级频谱图。

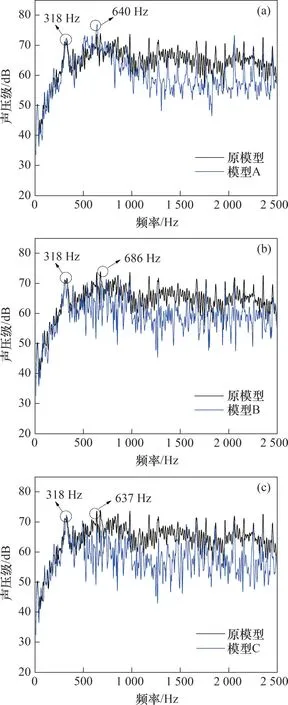
图14 测点(0，0，1.32)m处的A计权声压级频谱图Fig.14 Spectra of A-weighted sound pressure level at measuring points(0,0,1.32)m

由图14 可以看出：冷却风机的噪声属于宽频噪声，且存在与进风口和出风口叶片数及转速相关的离散噪声(各阶叶片通过噪声)；波浪形前缘结构可以降低冷却风机的离散噪声和宽频带噪声，且对宽频带噪声的降噪效果更好。离散噪声降低表明了风机内部气流的不稳定性有所提高，而宽频带噪声的降低表明由于风机表面边界层分离以及旋涡脱落所造成的压力脉动有所降低。结合涡声理论可以得到，波浪形前缘结构通过破坏前缘涡结构和抑制叶顶泄露流的强度，降低动车组轴流冷却风机的宽频噪声。

模型A，B和C降低宽频带的主要范围分别为1 000～2 500，500～2 500 和500～2 500 Hz；模型A，B 和C 在1 000～2 500 Hz 的降噪水平无明显差异，在500～1 000 Hz 范围的降噪量存在明显区别：随着波长减小，在500～1 000 Hz 范围内的降噪量逐渐增加。从图12 和图13 可知，模型A，B 和C 的声源强度的区别主要体现在叶片前缘处，叶顶处及后缘处的声源强度差别较小。因此可以推出：因气流冲击叶片前缘所造成的噪声主要集中在500～1 000 Hz范围内。

图15所示为冷却风机A计权声压级的1/3倍频程频谱图。

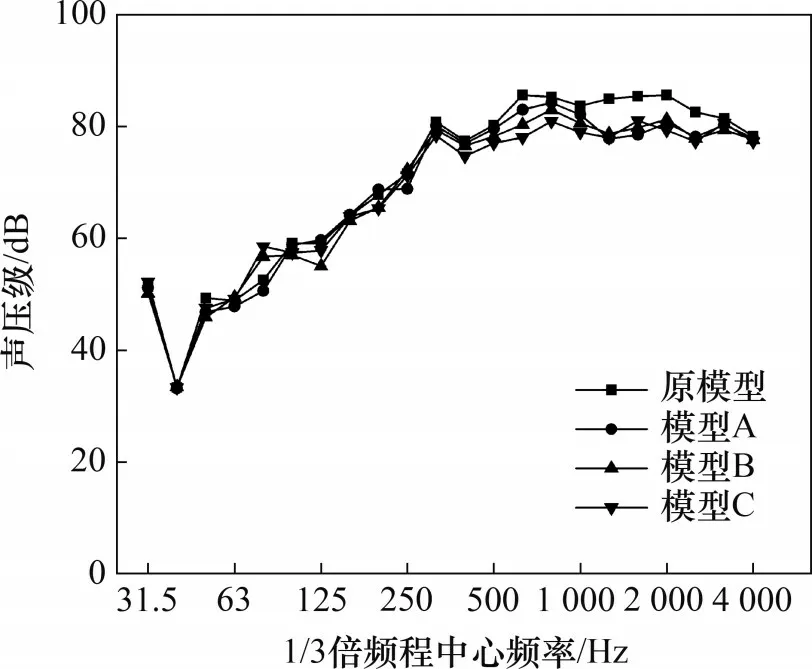
图15 冷却风机A计权声压级的1/3倍频程频谱图Fig.15 1/3 octave spectrum of A-weighted sound pressure level of cooling fan

由图15 可以看出：该风机噪声的声能量主要集中在31～5 000 Hz 频段内，在40～630 Hz 范围内声压级随频率增大而显著增加，峰值出现在中心频率为630 Hz 处；波浪形前缘结构主要降低了500～2 500 Hz 频段内的噪声；在1 250～2 500 Hz 频段内，模型A，B 和C 的降噪量大致相同，为4～8 dB；模型A，B 和C 在500～1 000 Hz 频段内的1/3 倍频程频谱图差异比较明显，其中，C 模型的降噪量最大，约为4.5 dB，其次是B模型，降噪量约为3 dB；A模型的降噪量最小，约为1 dB。

4 结论

1)波浪形前缘结构可提高原风机的气动性能，提高风机的流量和效率。

2)相对于原型风机来说，波浪形前缘结构对冷却风机流场的影响主要体现在3方面：波浪形前缘结构改变了叶片前缘处的压力梯度分布；波浪形前缘结构破坏了涡核的分布状态；波浪形前缘结构影响了叶顶泄漏流的强度和扩散路径。表现为波浪形前缘结构的波长越小，叶片前缘处的压力梯度分布越均匀，破碎形成的小涡越多，叶顶泄漏流的强度越小。

3)波浪形前缘结构通过破坏前缘处的涡结构、降低叶顶泄漏流的强度，从而降低了冷却风机的宽频噪声。本文设计3种叶片较原型叶片最大降噪量可达4.5 dB。