尾矿库漫顶溃坝机理与溃坝过程数值模拟

2022-08-29刘嘉欣阎志坤钟启明陈亮单熠博

中南大学学报（自然科学版） 2022年7期

刘嘉欣，阎志坤，钟启明,3，陈亮，单熠博

(1. 河海大学土木与交通学院，江苏南京，210098；2. 南京水利科学研究院岩土工程研究所，江苏南京，210024；3. 水利部土石坝破坏机理与防控技术重点实验室，江苏南京，210029)

我国采矿业在带来巨大经济效益的同时，也制造了大量废料，其中最主要的是尾矿。目前对尾矿的主流处置方法是筑坝存储，存储形成的结构物统称为尾矿库或尾矿坝。据统计，全国共有14 217座尾矿库，其中铁矿的尾矿库最多[1]。尾矿库运行状况与周围环境及居民生活关系密切，随着社会经济的发展，世界各国也越发重视尾矿库的建设和安全管理。据统计[2]，从2001 年至2015年，我国共发生尾矿库事故99 起，其中由洪水漫顶引发的溃坝事故占溃坝总数的35%。2008年9月8日，山西省襄汾县发生特别重大溃坝事故，造成277 人死亡、4 人失踪、33 人受伤，直接经济损失达9 619.2 万元[3]；2010 年9 月21 日，广东省茂名市信宜紫金矿业有限公司发生尾矿库溃坝事故，造成22 人死亡，523 户房屋倒塌，815 户房屋受损[4]；2019年1月25日，巴西米纳斯吉拉斯州布鲁马迪纽市发生铁矿石尾矿库溃坝事故，造成165人死亡、160 人失踪[5]。目前，对尾矿库溃坝的研究大多借鉴土石坝溃坝的研究成果[6]，但尾矿库的坝料特性和构筑方式均与土石坝的不同，尾矿库溃坝时的溃口下泄物固相含量较高，且其失事概率也比水库大坝的失事概率高10 倍以上[7]。现有的针对尾矿库的模型试验研究主要集中在尾矿库失稳和溃坝后泥石流演进等方面[8-12]，有关漫顶溃坝洪水流量变化过程和溃口发展过程的研究较少。数值模拟也主要集中在对坝体稳定性的研究[13]和溃坝事故后流体运动规律的研究[14-16]，对溃坝过程的精细化模拟方法的研究较少。

综上所述，我国尾矿库存在数量多、事故频发的现状，且人们对尾矿库的溃坝机理的认识不够清晰，考虑流固耦合的尾矿库溃坝过程数值模拟方法较少。为保护环境、保障人民生命财产安全，有必要深入研究尾矿库的漫顶溃坝机理，建立能够有效模拟溃坝过程的精细化数值模拟方法，提高溃口流量过程和溃口发展过程的预测精度，以期为科学制定应急预案提供理论与技术支撑。

1 尾矿库漫顶溃坝机理

物理模型试验是揭示尾矿库溃坝机理的有效方式，但尾矿库溃坝过程的模拟涉及材料力学、岩土力学、流体力学等多个学科，需综合考虑多个物理量的相似关系，在技术上存在一定难度，故有关尾矿库溃坝机理与溃坝过程的模型试验研究仍处于起步阶段。张红武等[17]认为对于尾矿库溃坝模型，设计时应考虑水流重力相似、水流阻力相似、水流挟砂相似、尾矿料悬移相似、河床变形相似及尾矿料起动相似，并提出了模型砂的选择及模型试验方法。武立功等[18]按1∶100的缩尺比探究不同粒径尾砂筑坝的尾矿库发生漫顶溃决时的溃决机理。赵怀刚等[19]将某尾矿库及下游河道整体按1∶400 比例进行缩尺，研究山地复杂地形条件下尾矿库溃决过程及溃后泥石流的演进规律。但现有的模型试验缩尺比例较小，存在重力不相似等问题[20]，使得试验结果与真实溃决机理存在偏差。

离心模型试验通过高速旋转的离心机所产生的离心力大幅提高模型的应力水平，使模型试验结果与原型结果更为接近，因此，离心模型试验在岩土工程中应用较多。陈生水等[21-22]基于南京水利科学研究院研制的溃坝离心模型试验系统开展溃坝离心模型试验，揭示了尾矿库的漫顶溃坝机理和溃口流量过程线，并得到了溃坝过程中的溃口演化规律。

1.1 模型试验设计

1.1.1 溃坝离心模型试验系统

离心机高速旋转所产生的N倍重力加速度场，使得土工构筑物几何尺寸缩小N倍后，模型和原型的应力水平相同。模型与原型之间通过相似准则进行连接，相似准则是用模型试验结果反推原型力学行为的理论依据。溃坝是水土耦合作用过程，需要依据能量守恒定律建立坝料和溃坝水流的离心试验相似准则，本试验中模型参数与原型参数相似比见表1。

表1 溃坝离心模型试验中模型参数与原型参数相似比Table 1 Similarity criterion between model and prototype parameters in centrifugal model test of dam breach

以南京水利科学研究院大型土工离心机(NHRI-400 GT)为基础构建试验系统，该系统主要由离心机大流量水流控制系统、溃坝试验专用模型箱以及数据采集与视频监控系统组成(见图1[23])。

图1 NHRI-400 GT溃坝离心模型试验系统示意图[23]Fig.1 Schematic diagram of NHRI-400 GT dam breach centrifugal model test system[23]

离心机大流量水流控制系统由贮水箱、接水环、伺服水阀、流量计和管路等组成(见图2)。该系统具有如下特点：1)在离心机大臂上设置接水环，解决了固定件与旋转件之间的磨损和渗漏问题，保证了高重力场下接水环内部水流的受力均匀，实现了水流从地面环境到高重力场之间的平稳过渡；2)研发伺服水阀流量控制装置可实现溃坝过程中入库流量的准确控制，实测流量与目标流量最大相对误差控制在1%以内。

图2 离心机大流量水流控制系统Fig.2 Large flow control system for centrifuge

溃坝试验专用模型箱的特点在于将薄壁量水堰内嵌于模型箱端板，实现了溃口流量的精确测量。模型箱内部有效长×宽×高为1 200 mm×400 mm×800 mm，一侧设置有机玻璃，薄壁堰口下游面与上游直立面成30°夹角，堰口宽度为280 mm，堰顶至模型箱底的距离为200 mm(见图3)。为了在超重力环境中测量堰前水头，在模型箱中放置水压力传感器(见图4)。采用动态数据采集与传输技术以及视频实时监测系统和基于粒子图像测量技术(PIV)的图像测量系统，构建数据采集传输与图像监控系统，以实现溃坝过程的多角度监测和摄录。

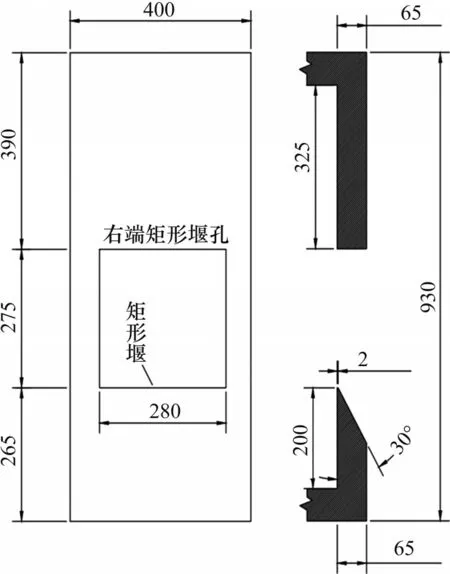
图3 薄壁量水堰尺寸Fig.3 Size of thin-wall water measuring weir

图4 水压力传感器Fig.4 Water pressure sensors

1.1.2 模型试验参数

本次离心模型试验所用尾矿料取自马钢集团姑山矿业公司青山林场尾矿库，通过筛分试验测得模型尾矿料中各粒组质量分数，见表2(其中d为粒径)。模型试验坝料级配曲线如图5 所示，模型试验尾矿料的基本物理力学特性参数见表3。

表3 离心模型试验尾矿料基本特性参数Table 3 Basic characteristic parameters of tailings for centrifugal model test

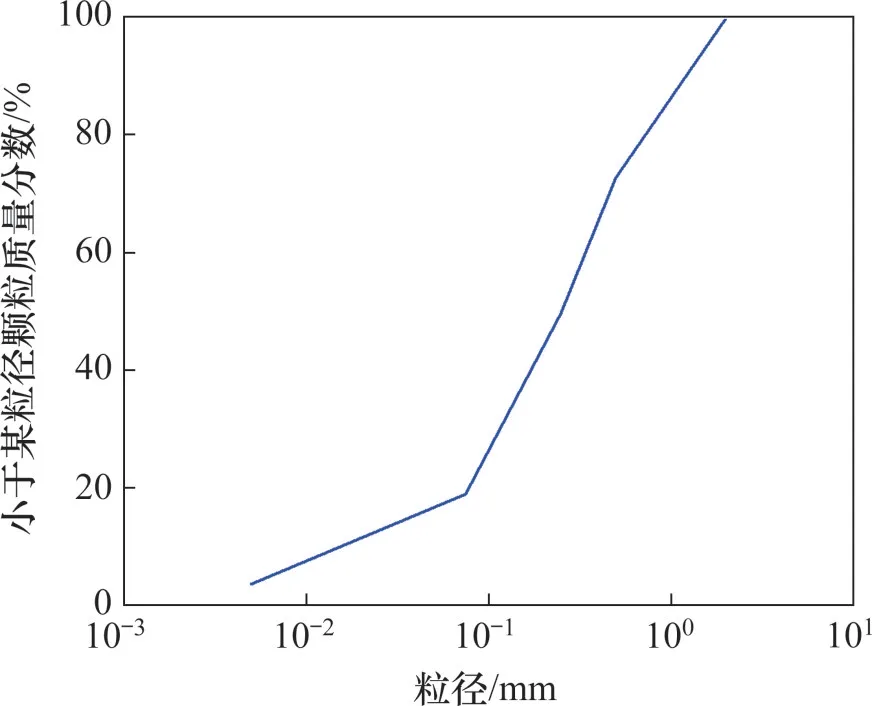
图5 模型试验坝料级配曲线Fig.5 Gradation curve of model test dam material

表2 模型试验坝料各粒组质量分数Table 2 Each granule group of dam material in model tests %

尾矿库不存在显著的上游坝坡，且库区内尾矿料自然沉积时间较短，固结较弱，以水砂混合为主，库容量小。考虑到尾矿库的材料、结构特点以及试验研究内容，模型主要考虑干滩面、坝顶和下游坝坡部分。

离心模型试验主要研究漫顶水流对尾矿库坝顶和下游坡溃口的冲刷影响，测量溃口发展过程和溃口流量变化过程相关参数等。离心模型试验设计A，B 和C 这3 组模型，尾矿库试验坝参数见表4。

表4 尾矿库溃坝离心模型试验坝参数Table 4 Parameter values of tailings dams breaching for centrifugal model tests

模型A 不设初始溃口，用来观察溃口的形成和发展过程；模型B在坝顶靠近模型箱有机玻璃一侧开挖一个顶宽为2 cm、底宽为1 cm、深度为1 cm 的倒梯形凹槽作为初始溃口，用来观测溃口的垂向发展过程；模型C在坝顶中间位置设置初始倒梯形溃口，初始溃口顶宽为4 cm、底宽为2 cm、深度为1 cm，观测溃口横向扩展过程。在模型上、下游设置圆开孔不锈钢板透水支撑边界。模型试验坝干密度为1.80 g/cm3，分层填筑，填筑完成后在上游库区内加水，保持水位在干滩面高度并静置24 h形成初始渗流场。下面选取模型B进行试验结果分析。

1.2 溃口演化规律

模型B成模后引导漫顶水流从右侧初始溃口处的坝顶开始冲刷，试验在50g(g为重力加速度)离心加速度条件下开展，通过对试验视频录像资料进行分帧处理，得到尾矿库溃口发展过程，如图6所示，尾矿库剖面形态演化过程如图7所示。由图7可以看出：溃口的最终深度为23.81 cm。

图7 尾矿库溃坝过程剖面形态演化示意图Fig.7 Profile morphologic evolution diagram of tailings dam breach process

根据尾矿库溃坝模型试验观测资料，可将溃坝过程分为如下3个阶段。

1)下游坡冲蚀(见图6(a)和6(b))。水流漫过坝顶后，沿最易冲蚀的路径运动，冲蚀下游坡面，形成许多细小的初始冲槽，冲槽内水流较小，溃口发展也相对较慢。2)溯源冲蚀(见图6(c)和6(d))。初始阶段的冲槽发展成较大的冲槽，并向上游发展至坝顶，冲槽内同时存在垂直下切和横向扩展现象，但下切速度要大于横向扩展的速度，以下切发育为主。3)沿程冲蚀(见图6(e)和6(f))。溃口水流主要作用于冲槽两侧边壁，侧壁连续冲刷和边坡坍塌交替发生，坍塌体逐渐被水流带走，当水流无法继续冲蚀坝料时溃坝过程停止，3组模型结果均显示溃坝结束时无残留坝高。综合试验模型A和C的结果可以看出：尾矿库溃口发展过程主要包括由水流冲刷引起的溃口快速下切和横向冲刷以及溃口边坡失稳坍塌引起的间歇性横向扩展。

图6 尾矿库溃坝离心模型试验过程Fig.6 Centrifugal model test processes of tailings dam breach

1.3 溃口流量变化过程

在溃坝过程的初始阶段，坝前水位上升，约10 s 后达到最高水位44.56 cm。由于溃口迅速发展，溃坝水流流量持续增加，库水位迅速下降。溃坝开始30 s左右，水位下降速度减缓，这主要是因为库水位已退至干滩面尾部，从模型C的试验结果可以看出，此阶段溃口呈“漏斗状”。40 s 后溃口发展到干滩面尾部，溃口流量迅速增加，库水位又迅速下降。此后，库水位下降速度随溃口发展逐步变缓，过程曲线呈“锯齿状”，这主要是由于溃口边坡大块滑坡导致溃坝水流的流量降低，外部入流作用导致水位短时间内抬升。离心模型试验溃口流量变化如图8所示。

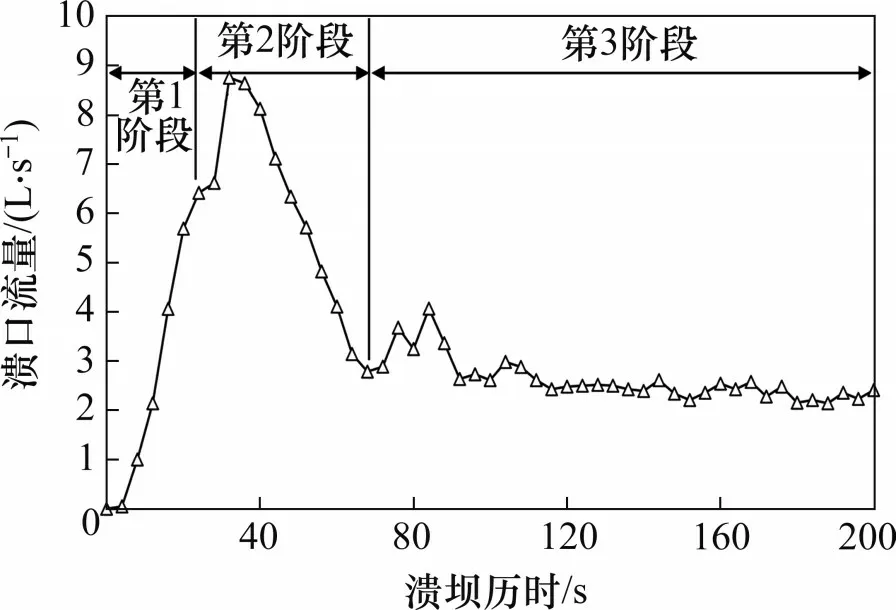
图8 尾矿库漫顶溃坝溃口流量变化Fig.8 Breach flow changes of tailings dam due to overtopping failure

由图8可以看出：溃坝初始阶段溃口流量快速增大，在溃坝32 s 时达到峰值流量8.75 L/s，此阶段溃口快速下切，这主要是因为汇水面积不断增大。在达到峰值流量之后的30 s内，溃口流量迅速下降，上一阶段较大的溃口流量使水位迅速下降至干滩面尾部底床附近，库中没有足够的水流迅速补充到溃口处，因此溃口流量迅速下降。

通过尾矿库溃坝离心模型试验可以看出，在水流作用下，尾矿库与均质土坝漫顶溃坝过程存在一定的相似之处，但由于尾矿库结构、材料的独特性，在溃坝水流作用下形成高浓度水流，溃口下切速度非常快，破坏能力更强，溃口发展规律和流量过程更复杂。因此，针对尾矿库漫顶溃坝的数值模拟要重点考虑水流运动与尾矿料输移的相互作用。

2 数学模型

2.1 数学模型控制方程

基于静水压力假设的二维浅水方程可作为描述溃口流量的控制方程[27-29]。但由于尾矿库溃口下泄物中的固相含量较高，需要考虑挟砂水流的冲蚀对溃口形态演化的影响。因此，在浅水方程中引入挟砂水流的浓度，进而可考虑水流、坝料和溃口底床变化的耦合作用，控制方程如下：

式中：Φ为守恒变量，Φ=[h,uh,vh,hCt]T；F(Φ)和G(Φ) 为单元界面的法向通量，F(Φ)=[uh,u2h,uvh,huCt]T，G(Φ)=[vh,uvh,v2h,hvCt]T；S(Φ)为源项，S(Φ)=[s1,s2,s3,s4]T；s1，s2，s3和s4可分别表示为

其中，h为溃口水深；u和v分别为x和y方向的平均流速；Ct为挟砂水流质量浓度；pm为溃口处坝体孔隙率；U为深度平均流速；mb为溃口底床的坡度系数，mb=[1+(∂zb/∂x)2+(∂zb/∂y)2]1/2；qt*为坝料冲蚀率；L为坝料冲蚀从非平衡到平衡状态的适应长度；ρw为水的密度；ρs为坝料的密度；g为重力加速度。

2.2 数学模型求解

2.2.1 控制方程离散

模型的控制方程采用矩形网格上的Godunov型格式有限体积法计算。式(1)的离散化方程为

由于控制方程中含有考虑流固耦合和河床变化影响的源项，为方便起见，将控制方程分为齐次偏微分方程和常微分方程。

2.2.2 通量计算

本研究通过前瞻性队列研究，在 435例乙型肝炎病毒感染患者中进一步探讨和验证了 2型糖尿病与乙型肝炎病毒相关肝癌发病的关系，并提供了 2型糖尿病与乙型肝炎病毒相关肝癌发病风险的前瞻性研究证据。但本研究也存在一定的局限性，如没有考虑糖尿病病程、糖尿病用药、抗病毒治疗等因素对研究结果的影响，因此尚需纳入相关因素进一步开展更大样本量的研究。总之，在本队列人群中，2型糖尿病和乙型肝炎病毒相关肝癌发病有关，2型糖尿病增加了乙型肝炎病毒感染患者的肝癌发病风险。

有限体积算法的关键是如何计算通过界面的流体的流量通量和动量通量以及尾矿料流量通量。有限体积法不存在守恒误差，其主要误差来自网格单元界面上通量计算误差。对于齐次偏微分方程，采用HLLC黎曼求解器计算流体质量和动量的网格界面通量。

图9 二维有限体积网格Fig.9 Two dimensional finite volume mesh

尾矿料流量通量不采用黎曼求解器，界面上尾矿料通量为水流通量与尾矿料质量浓度的乘积。相邻2个计算单元界面只有一个水流通量，而界面左右两侧存在2种尾矿料质量浓度，尾矿料的界面通量可以通过中波速SM与0的关系来确定[31]：

2.2.3 数值重构

为了在空间上达到二阶精度，选择一种分段线性数值重构的方法(MUSCL 格式)提高解的空间精度[32]。为了避免出现大梯度下的假振荡现象，采用全变分衰减(TVD)格式来描述振荡[33]，利用坡度限制器Δ͂i来控制变量或通量的梯度。

2.2.4 源项离散

由于模型控制方程分解为齐次偏微分方程和常微分方程，所以源项采用直接离散处理。源项离散方式对数值解的精度有很大的影响，模型控制方程中的源项主要包括水面梯度项、溃口底床摩擦阻力项、浓度梯度项等。

溃口底床坡度在静水条件下会产生虚假流动现象，故采用改进的表面梯度法(SGM)计算水面梯度项[35]。

为了得到稳定的计算结果，采用半隐式格式计算溃口底床摩擦阻力项[27,36]。

此外，采用中心差分格式处理浓度梯度项，以获得二阶精度[27,37]。

2.2.5 尾矿料冲蚀率

由式(1)可知：影响冲蚀过程的关键输入参数为L和qt*。L可通过下式[38]确定：

式中：Lb为推移质自适应长度；α为悬移质自适应系数。

尾矿料冲蚀率qt*包括悬移质冲蚀率qs*和推移质冲蚀率qb*这2 个部分，悬移质冲蚀率可通过下式[39]计算：

式中：Φs为量纲一悬移质冲蚀率；γs和γ分别为尾矿料和混合物的容重；d50为尾矿料平均粒径；τ为流体剪应力，τ=γRJ；R为水力半径；J为能坡；τc为尾矿料的临界起动剪应力。

同理，推移质冲蚀率可通过下式[39]计算：

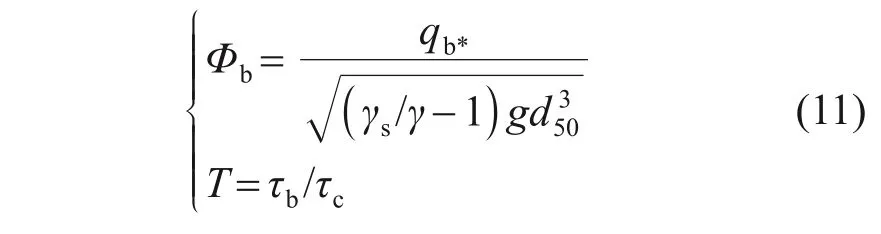
式中：Φb为量纲一推移质冲蚀率；τb为溃口床面的流体剪应力，τb=ρgN2mbU2/h1/3；N为曼宁糙率系数。

当坝体坡度较陡时，需要考虑重力分量对尾矿料起动条件和冲蚀率的影响。采用考虑重力影响的方法对τb和τc进行修正[40]。

式中：τbm和τcm分别为溃口床面的流体剪应力修正值和尾砂料临界剪应力修正值；φ为尾矿料的休止角；θ为坝体边坡坡角；cosωz为平面流动方向上河床高程的梯度。

2.2.6 溃口边坡失稳

随着尾矿库溃坝的持续，溃口边坡可能发生失稳，模型采用矩形网格上二维边坡滑动的数值计算方法[31,37]，即当相邻网格中心点连线的坡角大于尾矿料休止角时，边坡将发生滑坡，形成溃口底床，其方程表达式如下：

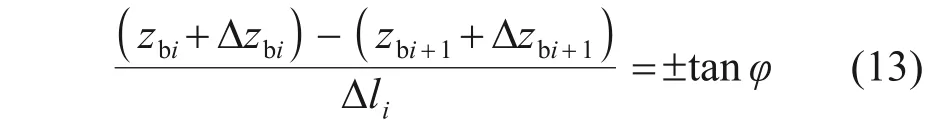
式中：zbi和zbi+1分别为计算点i和i+1的溃口底床高程；Δzbi和Δzbi+1分别为滑坡造成的计算点i和i+1的溃口底床高程变化量；Δli为计算点i和i+1 之间的距离；当计算点i至i+1 为上坡方向时，tanφ取正值，当计算点i至i+1 为下坡方向时，tanφ取负值。

若8 个相邻网格中有1 个以上满足滑坡条件，则将这些网格分为上坡网格和下坡网格。相邻网格的床面高程变化可用下式表示：

式中：Nup和Ndown分别为上坡和下坡网格数。

同时，中心网格与8个相邻单元上滑坡尾矿料总质量应满足质量守恒定律：

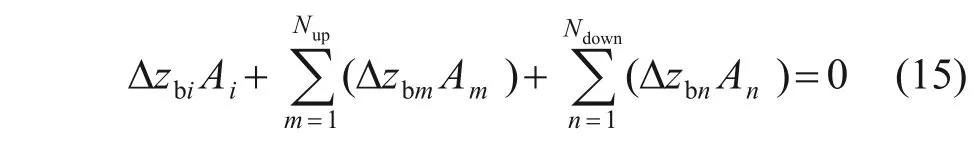
由滑坡条件和质量守恒定律可以得到中心网格底高程变化量的表达式：

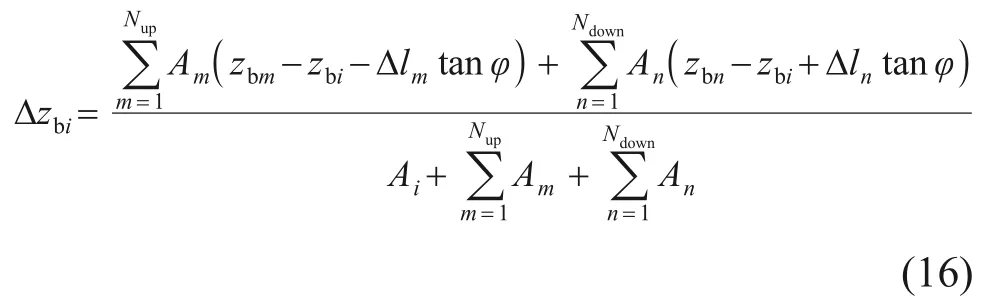
2.2.7 模型稳定性判定

在计算迭代步骤中，若溃口底床高程变化量Δzb过大，则无法保证尾矿料冲蚀率计算结果的准确性[41]；经调试发现Δzb应小于水深的10%。此外，为了保证计算效率，采用动态时间步长方法，即在每次迭代前，模型通过式(17)为迭代计算选择最优时间步长。

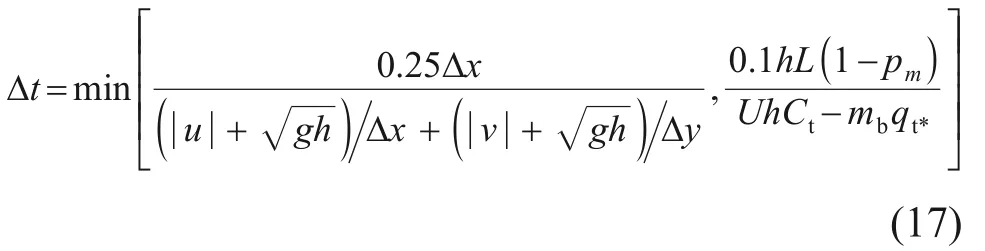
2.2.8 数值模拟流程

尾矿库漫顶溃决过程数值模拟计算流程图如图10所示。

图10 尾矿库漫顶溃决过程数值模拟流程图Fig.10 Numerical simulation flow chart of tailings dam overtopping breach process

3 漫顶溃决过程数学模型验证

为了验证基于尾矿库溃坝机理的数学模型和数值计算方法的合理性，首先选择双侧扩宽水槽中动床模型[42]进行试验，该模型试验常被学者们作为基准试验来验证流固耦合模型的准确性[27,43]。随后，选择尾矿库漫顶溃坝离心模型B进行试验，测试流固耦合模型的合理性。

3.1 双侧扩宽水槽中动床模型试验

本文选用文献[42]中的算例分析动床条件下溃坝水流引起的底床变化。水槽试验参数见表5，试验平面布置示意图如图11 所示。试验通过快速抽起1 m宽的闸门模拟溃坝过程，闸门两侧为不透水块，上、下游宽度均为1.0 m。水槽底床预先铺设饱和砂，铺设范围从溃口上游1 m至溃口下游9 m。以水槽定床为参考面，蓄水池初始水位为0.47 m。在溃口下游处预先布置8 个超声探头测量水位变化，测量点U1～U8具体坐标值见表6。

表5 水槽试验参数Table 5 Parameters for flume experiment

图11 水槽试验平面布置示意图[42]Fig.11 Schematic layout diagram of flume experiment[42]

表6 水位测量点坐标Table 6 Coordinates of water level measuring points

各监测点水位计算结果与实测结果对比如图12所示，最终水位实测值与计算值对比见表7。由图12 和表7 可以看出：数值计算模型较好地预测了各监测点水位变化。监测点U2和U3距离溃口较近，水流出现振荡趋势，结合底床变化来看，可能是由底床高程的剧烈变化所致。监测点U1和U4在水槽扩宽的位置，在初始阶段，水位数值计算结果明显低于实测值，监测点U5和U8的水位变化较为平稳。

表7 监测点最终水位测量值与计算值对比Table 7 Comparison of measured and calculated values of final water level at each monitoring point

图12 各监测点水位实测值与计算值变化过程对比Fig.12 Comparison of measured and calculated water level variations at each monitoring point

数值计算与实测的最终底床厚度对比如图13所示。由图13 可以看出：接近溃口的区域表现出较为明显的冲蚀特征，数值计算结果显示底床泥砂被挟砂水流全部带走，底床泥沙厚度接近于0 m，实测结果也在0.015 m 以下。下游水槽壁都表现出明显的沉积特征，当溃坝波传到水槽两侧，冲击侧壁形成水跃，水流强度降低，在下游和水侧两侧形成沉积特征，底床泥沙厚度为0.125～0.145 m，高于原始高度0.085 m，与实测结果相似。考虑到溃坝水流输砂过程的复杂性，可认为本文的模型较好地反映了挟砂水流作用下的冲蚀与沉积特征。

图13 实测与计算所得最终底床形状对比Fig.13 Comparison of measured and calculated morphologies of final bottom bed

3.2 尾矿库漫顶溃坝离心模型试验

为进一步验证模型计算的准确性，选取尾矿库漫顶溃坝离心模型B进行试验验证，模型B尾矿料特性和试验坝参数分别见表3 和表4，按照表1中的相似准则，将模型试验实测值转化为原型实测值。表8所示为不同参数实测值与计算值的对比结果。由表8可以看出不同参数相对误差均在±5%以内。

表8 尾矿库漫顶溃坝离心模型B不同参数实测值与计算值对比Table 8 Comparison of measured and calculated values of different parameters in centrifugal model B for overtopping breach of tailings dam

图14 所示为尾矿库溃坝溃口流量实测值与计算值对比，图15 所示为坝体纵断面溃口发展过程计算结果。由图14和图15可以看出：在溃坝开始初期，溃口发展缓慢，此阶段主要为下游坡冲蚀；随着溃坝的发展，溯源冲刷发展至坝顶溃口的位置，溃口在挟砂水流和边坡滑坡的交替作用下快速发展，下切速度快于横向发展的速度，此时段水位迅速下降；后续溃口流量逐渐减小，溃口发展速率减缓。由图14和图15可以看出：数值模拟得到的溃坝过程与离心模型试验结果基本吻合，验证了模型的合理性。