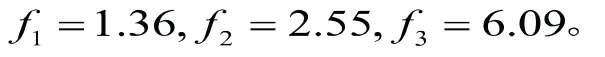基于可能性理论的模糊路径选择

吴祥标，张转周，许光俊

(遵义师范学院数学学院，贵州 遵义 563006)

1 引言

Teodorovic和Kikuchi首先将模糊逻辑用于路径选择，在模型中，他们将出行时间定义为模糊数，对于由两条路径组成的网络，用近似推理机获得每个驾驶员对路径的偏好，并研究了网络加载机制[1-3]。随后，文献[4-11]基于模糊集理论和近似推理，建立路径选择模型。

Henn基于可能性测度提出一个路径选择模型，并且定义了模糊用户均衡条件，即每条被配流的路径都具有几乎最小的近似路径成本，并认为这一条件可视为对UE的一般化[12]。在模糊用户均衡的基础上，本文通过对出行者的模糊路径选择行为的分析，得出了模糊用户均衡的等价条件。

2 可能性理论[13]

定义2.1在模糊理论中，Pos{A}描述了事件A发生的可能性。为了保证Pos{A}在实际中的合理性，它需要满足一些数学性质，其中有三条公理是必须满足的。假设为非空集合，R()表示的幂集：

3 模糊路径选择模型

Henn基于可能性测度提出一个路径选择模型，并且定义了模糊用户均衡条件，即每条被配流的路径都具有几乎最小的近似路径成本。那么，在模糊路径选择问题中，出行者是如何寻找到具有几乎最小的近似路径阻抗的路径呢？本文用可能性表示模糊事件发生的置信水平，则最短路就是几乎最小的近似路径阻抗的路径。

阻抗函数f(x,c)取最小值对应最短路径阻抗。阻抗函数f(x,c)通常定义为，x和c分别为包含决策变量xij和阻抗变量cij的向量。当cij为确定的数时，上述模型就是经典的最短路问题，可用最简单的优化方法求解。但是当cij为模糊变量时，就需要研究相应的建模方法和算法。

本文根据Henn定义的模糊用户均衡条件，将出行者模糊路径选择转化为寻找最短路径的过程。而最短路径问题的机会约束规划模型如下：

混合智能算法步骤如下：

1）用模糊模拟技术为不确定函数产生输入输出数据，

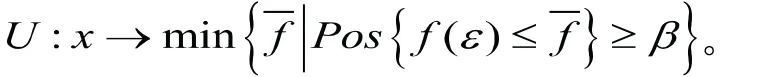
2）根据产生的数据训练一个神经元网络逼近不确定函数。

4）通过交叉和变异操作更新染色体，并利用训练好的神经元检验染色体的可行性。

5）利用训练好的神经元网络计算所有染色体的目标值。

6）根据目标值计算每个染色体的适应度。

7）通过旋转赌轮选择染色体。

8）重复步骤2只步骤7直到完成给定的循环次数。选择最好的染色体作为最优解。

示例3.1

考虑一个如图1所示的具有26个节点和44条弧的路网系统，其模糊路径阻抗（取值均为三角模糊数或梯形模糊数）如表1所示。

图1 路径图

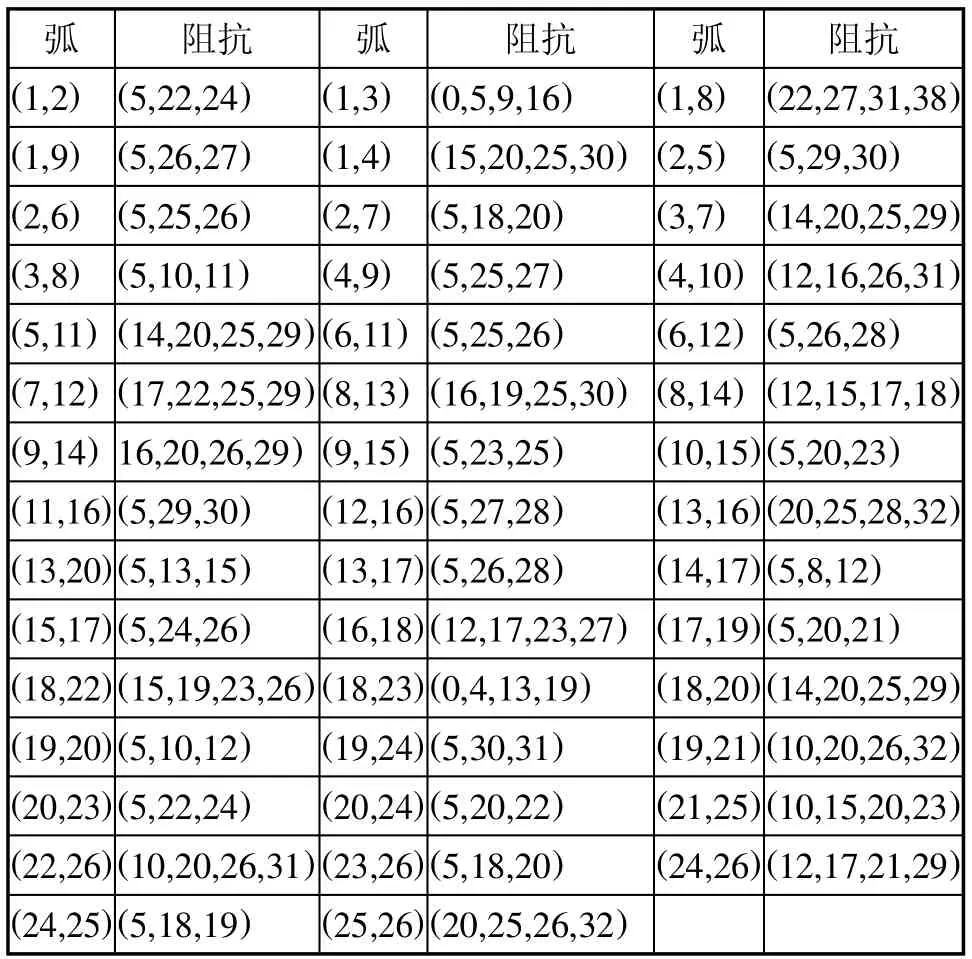
表1 阻抗表

通过运行混合智能算法（8000次循环模拟，1000次遗传迭代），得到如下最短路径：

4 模糊用户均衡

Henn基于可能性测度提出一个路径选择模型，并且定义了模糊用户均衡条件，即每条被配流的路径都具有几乎最小的近似路径成本。

根据上一章提出的FUE，很容易理解，在均衡点，如果路径k上的流量大于0，那么对应的路径感知阻抗“约等于”最小的路径感知阻抗；如果路径k上的流量等于0，则对应的路径感知阻抗可能大于，即

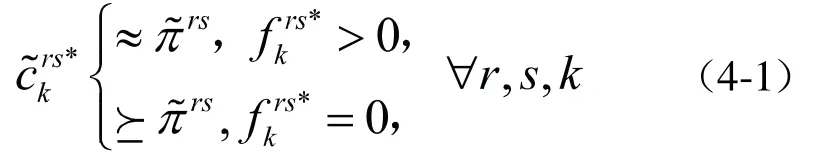
在上节中，讨论了出行者的模糊路径选择模型，即所有出行者都选择了最短路。则对于置信水平，可将条件（4-1）改写成

为了得到模糊用户均衡的解，本文采用如下算法：

下面用一个简单算例来说明本节提出的模糊随机用户均衡算法。

例4.1图2是一个只有一对O-D和三条路径（段）的简单路网。它们的阻抗函数如下：

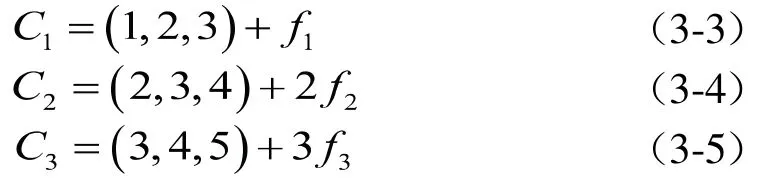
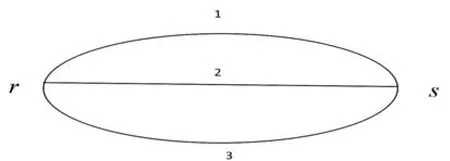
图2 一对O-D路径网

总O-D流量q=10，即：

计算过程如表2：

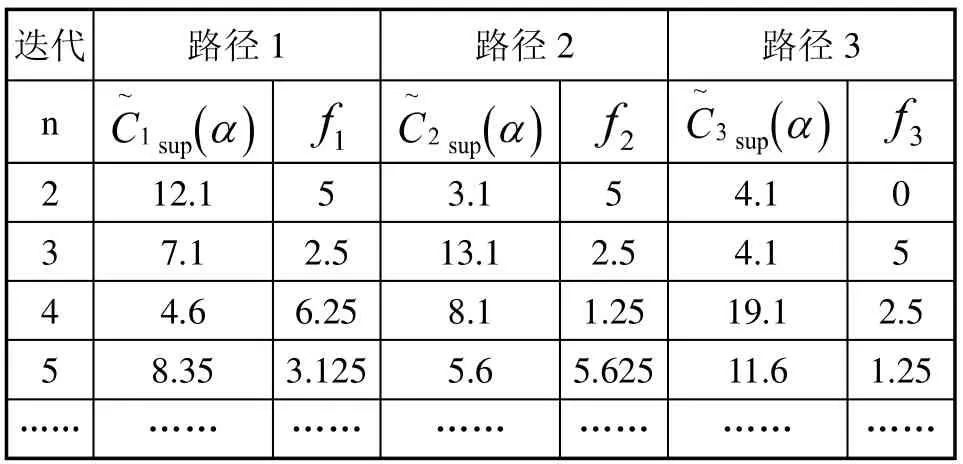
表2 迭代计算过程表

最终得到的解如下：