金属纳米柱的端面修饰对自发辐射增强特性的影响*

苏玉凤 彭金璋 杨红 黄勇刚

(吉首大学物理与机电工程学院,吉首 416000)

金属纳米柱具有优异的光学性能,其表面等离激元共振可通过纵横比灵活地调节,且能将光场局域到亚波长甚至纳米尺度,被广泛应用于自发辐射调控.然而,当纳米柱的端面形貌和材料不同时,附近量子点的自发辐射特性如何变化尚不明确.本文分别采用经典的德鲁德局域响应近似、非局域流体动力学模型和广义的非局域光响应模型,基于有限元方法,系统地研究金属纳米柱结构的端面形貌、尺寸以及材料对附近量子点自发辐射增强特性的影响.结果表明,当端面形貌由尖端逐渐变为圆柱时,自发辐射增强谱发生明显红移,峰值逐渐增大.相比于金纳米结构,当尖端材料由金改为银时,自发辐射增强谱蓝移,峰值略有降低,而当柱身也改为银时,即全银纳米结构,自发辐射增强谱大幅蓝移,峰值急剧增大.对于两种金属构成的核壳结构,壳层金属对内部金属表面等离激元共振具有屏蔽作用,随着壳层厚度的增大,核壳结构中表面等离激元共振逐渐接近壳层金属表面等离激元共振,对金纳米结构包覆银,共振峰蓝移,而对银纳米结构包覆金,共振峰红移.

1 引言

表面等离激元是入射光与金属表面的自由电子相互作用而产生的一种集体振荡,能把光场压缩在突破传统光学衍射极限的纳米尺度[1],被广泛用于减小光学器件尺寸[2]及增强光与物质的相互作用[3]等.随着纳米制备技术的发展[4-7],不同形状、尺寸和材料的金属纳米结构被可控地制备[8-10].相比于其他形貌的金属结构,纳米柱具有优异的光学性能[11-15],其共振特性可通过纵横比来调节,在诸多领域具有重要的应用,包括高灵敏传感器[16]、新型电磁超材料[17]、光学天线[18,19]等.

自发辐射是处于激发态的原子在真空零点场的作用下向基态跃迁辐射光子的过程[20-22],是诸多应用研究的基础.近年来,利用表面等离激元效应增强原子的自发辐射已成为研究热点,各种共振和非共振金属纳米结构被广泛采用[23-37],包括表面等离激元纳米天线、纳米腔、低折射率空隙和尖锐的金属结构等.其中,在金属纳米结构的表面引入大曲率结构来增强自发辐射备受关注,如在金属表面引入原子尺度凸起[35],由于“避雷针”效应,会产生极端局域模式,能获得极大的自发辐射增强;利用银包覆金纳米柱尖角处的局域场增强,已在单量子水平实现光与分子的强耦合[31].此外,Yang等[36]系统研究了针尖表面的原子尺度凸起对附近单分子荧光增强的重要作用,对于未做修饰的针尖,实验上不能观察到单个分子的荧光增强,而当针尖吸附单个银原子或团簇后,单分子荧光信号增强高达1.7×108,且能实现亚纳米分辨率成像.Rosławska等[38]系统分析了银纳米柱端面原子尺度凸起对附近分子兰姆位移和自发辐射增强的重要作用.这些研究表明,对金属表面进行修饰,如引入尖端结构,包覆不同金属等,可调控附近量子辐射体的发光特性.本文研究金属纳米柱表面修饰对附近原子自发辐射特性的影响.

理论上,金属中自由电子的光学响应通常采用基于局域响应近似(LRA)的德鲁德(Drude)模型[31,36-38].外电磁场作用下,感应电荷位于金属表面附近无限薄的区域,对于含有纳米或亚纳米尺度的金属结构,“避雷针”效应导致尖端处的电荷密度急剧增大,量子压效应凸显,由于自由电子气有限的可压缩性,经典局域响应模型有可能失效.借助流体动力学理论,将自由电子的集体运动用电荷密度和电流密度来描述,考虑量子压效应,可得到自由电子的非局域光响应模型[24,35,39,40].当在线性化电荷运动方程中引入Thomas-Fermi(TF)电子压力时,即为通常的非局域流体动力学模型(HDM)[41],利用此模型,可解释表面等离激元共振频率随尺寸减小而蓝移的现象.当纳米结构的尺寸小于电子的平均自由程时,界面散射效应显著,导致表面等离激元共振随尺寸的减小而展宽,通过引入扩散效应,可有效描述该耗散机制[42],此模型即为广义的非局域光响应模型(GNOR)[41].

本文主要运用有限元方法,结合经典的局域响应近似(LRA)、非局域流体动力学模型(HDM)和广义的非局域光响应模型(GNOR),研究金属纳米柱结构的端面修饰对附近二能级原子的自发辐射特性的影响,全文结构安排如下: 第2 节主要介绍了自发辐射的理论研究方法以及相关参数;第3 节研究了不同尖端结构的自发辐射增强特性,其中3.1 节系统研究不同几何参数时的自发辐射增强特性;3.2 与3.3 节中分别考虑了不同端面形貌及材料,在3.4 节进一步研究金属包覆尖端结构对自发辐射增强特性的影响.

2 理论

理论上[43],r处跃迁偶极矩为的二能级“原子”的自发辐射率可表示为

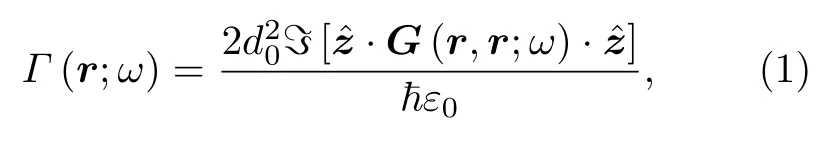
其中,ω为原子跃迁频率,G(r,r;ω)为光子并矢格林函数,可由经典振荡点电偶极子的辐射场表示为

其中,E(r,ω)为r0处的点电偶极子Pcdcδ(r-r0)在r处的辐射场,当经典振荡点电偶极子dc的方向也沿着zˆ 方向时,即dc,将(2)式代入(1)式可得:

此式为本文计算自发辐射率的核心.场E(r,ω),需借助于数值方法,类似于文献[24-26],人工微纳结构中,求解经典振荡偶极子的辐射本文采用基于有限元方法的软件COMSOL Multiphysics 求解.根据流体动力学模型[39],Maxwell 波方程和线性化的电荷运动方程满足:

欧姆电导率为σDiε0σγ/(ω+iγ),取L4,且参数与文献[44]一致,能较好地拟合实验数据.

β和D分别为电子简并压参数和扩散系数.当β0,D0 时,(5)式即为经典的欧姆定律J(r,ω)σDE(r,ω).当0,D0 时,为非局域光响应模型(HDM),本文取β对于金和银,费米速度为νF1.39×106m/s.而当00时,为广义非局域光响应模型(GNOR),金和银的扩散系数D分别为D1.90×10-4m2/s和D3.61×10-4m2/s[45].

3 模型及结果

如图1 所示,金属纳米结构具有旋转对称性,设旋转对称轴为Z轴,二能级辐射体 Q E (原子、分子、量子点等)位于该轴上,离金属表面的距离为h,他们的跃迁偶极矩沿zˆ 方向.由于该系统具有旋转对称性,角量子数守恒,可采用准二维计算方法[26,46],将电磁场分解为不同角量子数m的谐波,在二维横截面上求解.考虑到系统与方位角无关,只包含m0的谐波,因此,该三维问题可简化为二维问题,能极大减小计算量.

本文考虑不同的端面形貌及材料的纳米柱结构,金属选为金或者银,背景的相对介电常数为ε12.25,如图1 所示,设中间金属纳米柱的介电函数为ε2,半径为R,长度为L.图1(a)为纳米柱的上下有尖端结构,尖端高度为d,其介电函数为ε3,分别考虑尖端与柱身为同一金属(ε2ε3)和不同金属(ε2ε3);图1(b)为圆台结构,分别考虑不同的台面半径r(0 ≤r≤R),当r0 时,该结构退化为图1(a)所示的尖端结构,而当rR时,该结构为圆柱;图1(c)为介电函数ε2的双边尖端结构包覆介电函数为ε3、厚度为dceng的金属,研究核壳复合纳米结构的壳层与核的金属种类、壳层厚度等对自发辐射增强的影响;图1(d)为单边尖端包覆结构,内部材料介电函数为ε2,壳层介电函数为ε3、厚度为dceng.

图1 模型结构示意图 (a)双边尖端结构;(b)双边圆台结构;(c)双边尖端包覆结构;(d)单边尖端包覆结构.量子辐射体(Q E)位于纳米结构旋转对称轴上,离金属表面距离为 h,背景的介电常数 ε1=2.25 ,ε2和ε3 为金或者银的局域介电函数Fig.1.Schematic diagrams: (a)Cylindrical nanorod with two conical endcaps;(b)cylindrical nanorod with two truncated conical endcaps;(c)bimetal core-shell nanostructure that has the same shape as that in panel (a);(d)bimetal core-shell nanostructure that has the shape of a cylindrical nanorod with a single conical endcap.A quantum emitter (QE)is located on height h above the metal surface.The relative permittivity for the background is ε1=2.25 .ε2 and ε3 indicate the relative permittivity for two different metals,such as silver or gold.

3.1 双边尖端结构中的自发辐射增强特性

本节研究图1(a)所示的双边尖端结构,柱身和尖端均选为金,即ε2ε3ε金.首先研究柱身长度L对自发辐射增强Γ/Γ0(Γ0为均匀空间自发辐射率)的调控特性,为此,固定R10 nm,d10 nm和h10 nm.当L=40 nm 时,如图2(a)所示,相比于局域情况(LRA),非局域HDM和GNOR 模型下,自发辐射增强谱发生蓝移,其峰位由1.66 eV增大到 1.67 eV,约蓝移 0.01 eV,峰值略微降低,由LRA 模型下的 5 70.15 分别降为 5 32.53 (HDM)和498.67 (GNOR).而当柱身长度减小到L=20 nm 时,如图2(b)所示,相比于局域(LRA),非局域HDM和GNOR 下,峰位蓝移,由 1.99 eV增大到 2.02 eV,约蓝移 0.03 eV,大于L=40 nm 时的 0.01 eV,峰值由313.19 分别降为 2 51.32 (HDM)和2 27.69 (GNOR).

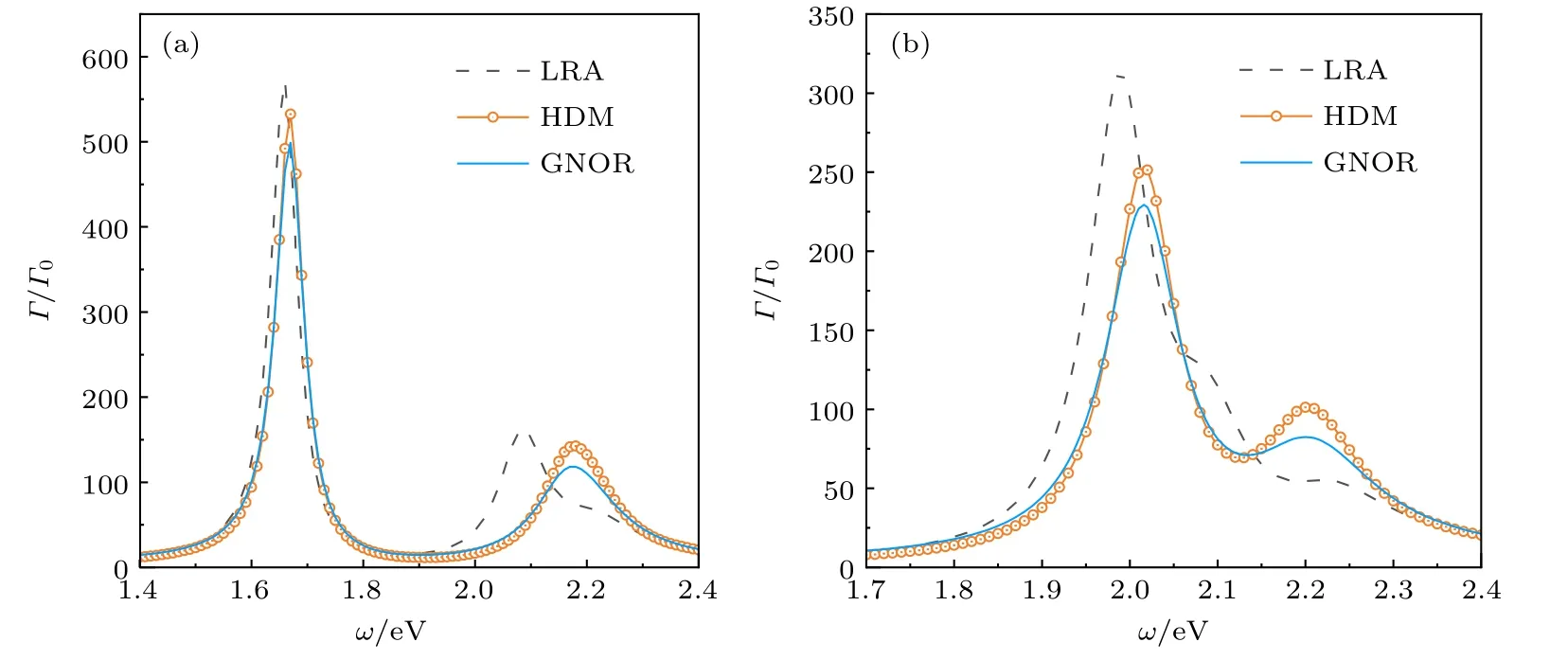
图2 不同长度双边尖端金纳米柱中的自发辐射增强谱 Γ/Γ0 (a)L=40 nm;(b)L=20 nmFig.2.Emission enhancement spectra Γ/Γ0 for nanostructures of two different length: (a)L=40 nm;(b)L=20 nm .The schematic diagram for the nanostructure is shown in Fig.1(a).

物理上,该自发辐射增强峰来源于纵向偶极表面等离激元共振,外电场作用下,纳米柱中的感应电荷在两个端面间来回反射,形成准一维的法珀共振[24],偶极共振条件为

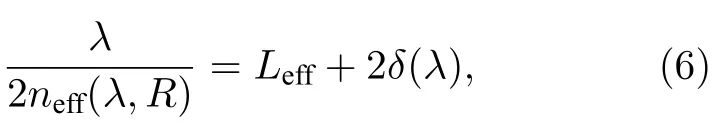
其中,λ为共振波长,neff(λ,R)是当工作波长为λ时,半径为R的波导中最低阶模式有效折射率的实部,Leff为纳米柱的有效长度,对于无端面修饰的圆柱,LeffL,由于端面修饰,Leff略大于L,δ为金属表面外位移电流的衰减长度.非局域量子压力作用下,尖端处的感应电荷向纳米柱中心移动,等效腔长Leff减小ΔL(一般几个埃),导致共振波长减小,共振能量蓝移Δω ∝[24](ω0为局域共振频率).因此,相比于局域LRA,非局域HDM和GNOR中,共振能量蓝移,越短的波导,共振频率越高,蓝移现象越明显.相比于HDM,GNOR 中的扩散作用能较好地描述界面散射效应,表面等离激元耗散增大,峰值降低.此外,等效腔长Leff减小导致感应偶极矩减小,散射场减小,自发辐射增强减弱[24].因此,随着柱身长度的减小,共振频率急剧增大,自发辐射增强急剧减小,非局域效应越来越明显,蓝移越大.

接下来固定L20 nm,进一步研究量子点离金属表面的距离h、尖端高度d和半径R对自发辐射增强的影响.图3(a)和图3(b)分别给出LRA和GNOR 模型下量子点距离h对自发辐射增强Γ/Γ0的影响,此时固定d10 nm,R10 nm .随着量子点接近尖端,如当h由 1 0 nm 变为 6 nm 时,LRA 模型下自发辐射增强峰值由 3 13.19 增加到 1 360.08,GNOR 下峰值由 2 27.69 增加到 8 65.03 .这主要是由于表面等离激元共振的模场被束缚在金属表面附近,远离金属表面(h增大),其模式电场强度呈指数衰减,与原子的相互作用减弱,自发辐射增强效应减小.

图3(c)和图3(d)分别给出LRA和GNOR 下尖端高度d对自发辐射增强特性的影响,此时固定R10 nm,h10 nm.随着d逐渐增大,无论是局域还是非局域,自发辐射增强谱红移,峰值急剧增大.如当d由 0 nm 变为 1 0 nm 时,LRA 模型下,峰位由 2.07 eV降低到 1.99 eV,约红移 0.08 eV,峰值由 3 2.38 增加至 3 13.19,约提高了10 倍.同样地,在GNOR 模型下峰位由 2.11 eV降低到 2.02 eV,峰值由 2 6.95 增加至 2 27.69 .以上结果可由(6)式理解,随着d的增大,等效腔长变长,共振波长变长,散射能力变强,与原子相互作用增强,自发辐射增强峰值增大.

以本院2017年1月到2018年1月收治的78例胸外科患者为研究对象，将所有胸外科患者按照随机数字表随机常规组与实验组，每组39例，所有患者均行右上肺切除术，排除肺部感染、肺心病、胸廓畸形、有胸部手术史的患者。78例胸外科患者在年龄、性别等一般资料方面均无明显差异，不具有统计学意义(p>0.05)。

图3(e)和图3(f)分别为LRA和GNOR 下纳米柱半径R对自发辐射增强的影响,此时固定h10 nm,d10 nm.随着半径R逐渐变小,无论是局域还是非局域,自发辐射增强谱急剧红移,峰值急剧增大.如当R由 1 0 nm 减小到 6 nm 时,LRA 模型下峰位由 1.99 eV降低到 1.63 eV,约红移 0.36 eV,峰值由 3 13.19 增加到 9 08.50 .类似于LRA,GNOR下峰位由 2.02 eV降低到 1.67 eV,峰值由 2 27.69 增加到 5 82.33.这主要是由于随着半径R的减小,纳米柱波导中等效折射率的实部neff急剧增大[24],由(6)式可以看出,共振波长急剧增大.此外,R减小,d不变,尖端结构变尖,避雷针效应更加显著,端面上的感应电荷密度增大,端面附近场增强效应越明显.

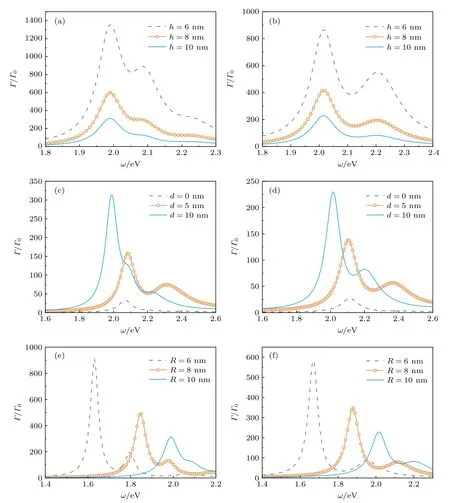
图3 不同几何参数下的自发辐射增强谱 Γ/Γ0 (a),(b)量子点离金属表面的距离 h;(c),(d)尖端高度 d;(e),(f)纳米柱半径R.左栏为LRA,右栏为GNORFig.3.Emission enhancement spectra Γ/Γ0 at different geometrical parameters: (a),(b)different Q E-surface distances h;(c),(d)different cone heights d;(e),(f)different nanorod radius R .The left column is for the LRA and the right column is for the GNOR.

3.2 端面形貌对自发辐射增强特性的影响

本节研究图1(b)所示的双边圆台结构.不同的台面半径r对应不同的端面形貌.图4 分别给出了r0,2,4,6,10 nm 时的自发辐射增强特性.当r逐渐增大,端面由尖端(r0 nm ),变为圆台(r2,4,6 nm ),最终变为圆柱(r10 nm),自发辐射增强谱发生明显的红移,峰值显著增大.LRA 模型下,如图4(a)所示,峰位由 1.99 eV降低到 1.74 eV,峰值由 3 13.19 增大到 7 80.03 .类似于LRA,在GNOR 模型下,峰位由 2.02 eV降低到 1.76 eV,峰值由 2 27.69 增大到 6 88.01 .相比于LRA,非局域自发辐射增强谱发生较小的蓝移,约为 0.03 eV,峰值略微降低.物理上,由于我们考虑的台面半径均较小,端面不足以承载感应电荷[24,47],随着r的减小,台面上的感应电荷急剧减少,散射场减弱,对自发辐射的增强效应降低,纳米柱的有效长度Leff减小,共振峰急剧蓝移.

图4 双边圆台结构的端面半径对自发辐射增强 Γ/Γ0 特性的影响 (a)LRA;(b)GNOR.其中,r为圆台端面半径,当r=0 nm时,该结构为双边尖端结构,当 r=10 nm 时为圆柱结构,当 r=2,4,6 nm 时为圆台结构Fig.4.Emission enhancement spectra Γ/Γ0 for different radius r at the endcaps (see Fig.1(b)): (a)LRA;(b)GNOR.When r=0 nm,the endcaps are of a cone shape.When r=10 nm,the nanostructure becomes a nanorod.When r is between them,the nanostructure is a cylindrical nanorod with two truncated conical endcaps.

3.3 材料对自发辐射增强特性的影响

对图1(a)所示的尖端结构,本节研究金属材料对自发辐射增强特性的影响.金属的介电函数ε(ω)直接影响表面等离激元共振特性,对于形状相同的金、银纳米结构,因其介电函数不同,银纳米结构的共振频率通常高于金.图5 给出了不同材料构成的双边尖端结构对自发辐射增强特性的影响.当尖端和柱身均为金时,如图5(a)所示,局域和非局域下,自发辐射增强谱的低阶峰分别位于 1.99和2.02 eV;当端面材料由金换为银时,如图5(b)所示,局域和非局域峰均稍稍蓝移,分别为 2.04和2.06 eV,峰值均降低,LRA 下由 3 13.19 下降到180.35,GNOR 模型由 2 27.69 下降到 1 46.23;而当柱身也为银,即全银结构时,如图5(c)所示,自发辐射增强峰发生急剧蓝移,局域和非局域模型下,分别增加到 2.40和2.45 eV,相比于图5(a)和图5(b),约蓝移 0.40 eV,自发辐射增强急剧增大,约提高2 倍;当端面材料为金,柱身为银时,如图5(d)所示,自发辐射增强谱与图5(a)类似,局域和非局域下,峰位分别为 2.07和2.17 eV,峰值分别为249.15和1 88.98 .以上结果表明:相比于异种金属,当尖端和柱身为同种金属时,自发辐射增强大,且银纳米结构中的增强效应大于金.

图5 双边尖端结构中,不同金属对自发辐射增强 Γ/Γ0 特性的影响.纳米结构的材料为 (a)金,(b)金柱身银尖端,(c)银,(d)银柱身金尖端Fig.5.Emission enhancement spectra Γ/Γ0 for nanostructure (see the insets)composed of different metal materials.The materials are (a)gold,(b)gold cylindrical nanorod and two silver conical endcaps,(c)silver,(d)silver cylindrical nanorod and two gold conical endcaps.

为理解以上现象,基于局域响应,采用模式分析,研究了半径为R10 nm 的金和银纳米线波导的工作特性.当ω2.0 eV 时,最低阶模式的有效折射率分别为7.41+0.49i (金)和5.09+0.04i (银),相比于金,银波导有效折射率的实部小,由(6)式可知,共振波长短,频率高.对于有效折射率的虚部,银波导远远小于金波导,约小一个数量级,且随着频率的增大,银波导中有效折射率的虚部缓慢增大,而金波导中急剧增大,如当ω2.5 eV时,金波导中,有效折射率的虚部比银大两个数量级,这主要是由于金的带间跃迁频率低[44],当ω＞2.0 eV 时,金的带间跃迁导致欧姆损耗大.由(6)式可知,相同尺寸的金和银纳米结构,银中表面等离激元共振频率大,当频率ω＞2.0 eV 时,金中的欧姆损耗显著.

基于准正则模理论,进一步计算了上述结构的表面等离激元准正则模式.由文献[37]可知,自发辐射增强可归结为一系列准正则模式贡献的和,即

图6 旋转对称轴上,实等效模体积 R e{1/Vk}随着金属表面距离 z 的变化情况.插图为纳米结构中最低阶模式的Ez分量.黑色点划线(Ag)和蓝色实线(Au)分别代表银和金双边尖端纳米结构,红色虚线(Ag-Au-Ag)代表银尖端金纳米柱结构,绿色点线(Au-Ag-Au)代表金尖端银纳米柱结构Fig.6.The effective real mode volume R e{1/Vk}as a function of the distance z between the QE and the metal surface.The inset is for the Ez component of the fundamental quasi normal mode.The black dash-doted line (Ag)and the blue solid line (Au)stand for silver and gold,respectively.The red dashed line (Ag-Au-Ag)stands for the gold cylinder with silver endcaps.The green dotted line(Au-Ag-Au)stands for the silver nanorod with gold endcaps.

3.4 双边尖端包覆对自发辐射增强特性的影响

图7 银包覆金结构中的自发辐射增强 Γ/Γ0 特性 (a)dceng=1 nm;(b)LRA 下,dceng=1, 2, 3, 4 nm;(c)与(d)分别为图(a)结构中的两个表面等离激元准正则模式的 Ez 分量Fig.7.Emission enhancement spectra Γ/Γ0 for a gold nanostructure coated with silver (see the inset in (a)): (a)dceng=1 nm;(b)dceng=1, 2, 3,4 nm under the LRA;(c)and (d)are for the Ez component of the two quasi normal modes on the cross section.

接下来研究金包覆银复合结构.相比于未包覆情况(图5(c)),当金包覆层厚度dceng1 nm 时,如图8(a)所示,自发辐射增强谱发生急剧红移,LRA模型下峰位由 2.40 eV(未包覆)降低到 2.14 eV (包覆),非常接近金纳米颗粒的峰位(2.002 eV),自发辐射增强急剧降低,由 5 84.17 降为 1 17.54,随着金包覆层厚度的增加,如图8(b)所示,共振频率发生缓慢红移.类似于银包覆金结构,金包覆层对内部银纳米结构的表面等离激元共振具有屏蔽效应,随着包覆层厚度的增加,屏蔽效应越来越强,复合纳米结构的表面等离激元共振越来越接近包覆层金.准正则模式分析表明,局域模型下,图8(a)所示的两个峰分别来源于图8(c)和图8(d)所示的表面等离激元准正则模式,其最低阶模式与银包覆金复合结构类似(图7(c)所示),而高阶模式与银包金的高阶模式不同,如图8(d)所示,模场整体上与低阶模式类似,只是在尖端处,模式的Ez分量出现符号的变化,如图8(d)中放大所示,预示着该高阶模式可能来源于尖端处的极端局域模式[35].不同的是,在非局域HDM和GNOR 模型中,自发辐射增强谱中,仅存在一个峰,且位于 2.34 eV,其峰值高于局域情况,这可能是由于当考虑非局域时,图8(c)和图8(d)的模式频率比较接近.对其他的金包覆层厚度,这一现象也存在.

图8 金包覆银结构中的自发辐射增强 Γ/Γ0 特性 (a)dceng=1 nm;(b)LRA 下,dceng=1, 2, 3, 4 nm;(c)与(d)分别为图(a)结构中的两个表面等离激元准正则模式的 Ez 分量Fig.8.Emission enhancement spectra Γ/Γ0 for a silver nanostructure coated with gold (see the inset in (a)): (a)dceng=1 nm;(b)different shell thicknesses with dceng=1, 2, 3, 4 nm;(c)and (d)are for the Ez component of the two quasi normal modes on the cross section.

以上结果表明,包覆层对内部金属表面等离激元共振具有一定的屏蔽作用,包覆层厚度越厚,表面等离激元共振越接近包覆层金属的表面等离激元共振.对银包覆金结构中,包覆层越厚,越接近银纳米结构的共振频率,共振频率越高,而对金包覆银结构,包覆层越厚,越接近金纳米结构中的表面等离激元共振,共振频率越低.

最后研究了单边尖端包覆对自发辐射增强的影响.如图9(a)所示,相比于双边尖端包覆结构(橙色圆圈),单边尖端包覆中,自发辐射增强谱蓝移(蓝色实线),峰位由ω2.1 eV (双边包覆)增加到ω2.14 eV (单边包覆),而自发辐射增强峰值几乎不变.在GNOR 下,如图9(b)所示,与局域模型类似,自发辐射增强谱也稍稍蓝移,峰位由2.11 eV增大到 2.16 eV .相比于双边尖端结构,单边尖端结构的有效长度稍短,由(6)式可知,共振峰蓝移.

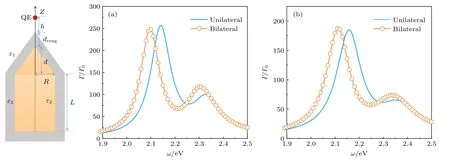
图9 银包覆金单边尖端结构中的自发辐射增强 Γ/Γ0 特性.结构示意图如左图所示,橙色圆圈代表银包覆双边金尖端结构中的结果,即图7(a)中的结果 (a)LRA;(b)GNORFig.9.The enhancement of the spontaneous emission rate Γ/Γ0 for nanostructure composed of gold core coated with silver.The schematic diagram is on the left,where the core is composed of a cylindrical nanorod with a single conical endcap.The orange line with dots represents the results shown in Fig.7(a)where there are two cones on both ends of the cylindrical nanorod: (a)LRA;(b)GNOR.

4 结论

本文系统研究了不同端面形貌、尺寸、材料的纳米柱结构中的自发辐射增强特性.对于双边尖端结构,纳米柱越长,半径越小,尖端越尖时,自发辐射增强谱的峰值频率越小,自发辐射增强峰值越高;当尖端和柱身为同种金属时,自发辐射增强较大,且银结构大于金.对于双边尖端包覆结构,包覆层对内部金属纳米结构的表面等离激元共振具有一定的屏蔽作用,包覆层越厚,屏蔽作用越明显,复合结构的表面等离激元共振越接近包覆层金属.随着包覆层厚度的增加,银包金纳米结构中表面等离激元共振频率蓝移,自发辐射增强峰值降低,而在金包银纳米结构中,共振频率红移,自发辐射增强峰值降低.与双边尖端包覆相比,单边尖端包覆中自发辐射增强谱稍稍蓝移.相比于局域LRA,非局域HDM和GNOR 模型下自发辐射增强谱蓝移.这些结果对于研究纳米柱结构中的自发辐射增强具有重要的指导意义.