气浮过程中气泡的聚并和破碎行为研究
2022-08-27于米满姬爱民
于米满,姬爱民
(华北理工大学 冶金与能源学院, 河北 唐山 063200)
气浮池作为一种有效的净水装置,包括接触区与分离区,其中接触区是气浮池中溶气水(即从饱和装置中流出的加压溶气水)与待处理污水开始相互接触的场所[1-2]。平流式气浮池净水系统示意图如图 1 所示,溶气水中被加压溶解的空气在接触区当中迅速释放出直径约为10~100 μm 的微小气泡,然后这些气泡迅速与污水中的颗粒物进行相互作用,最后气泡携带颗粒物在分离区中实现分离[3-4],达到降低污水中BOD、COD、SS 含量的目的。由于回流比、溶气压力、接触区中气泡的尺寸、浓度等参数对气浮分离效率起到决定性作用,因此需要对接触区中气泡的运动进行研究[5-7]。
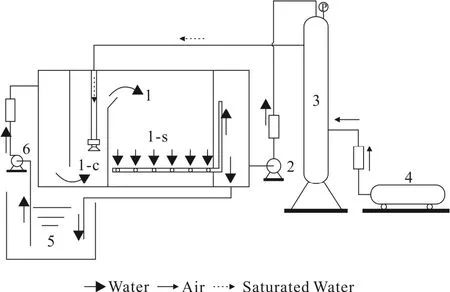
图1 平流式气浮池净水系统示意图[8]
目前关于气浮过程中气泡运动特性研究的焦点主要在于气浮过程的水力工况操作对气泡运动的影响,如陈阿强[9]等在仅考虑气泡聚并行为的前提下从液相速度梯度、污水处理量以及溶气水回流量对气泡聚并行为进行了数值仿真和实验研究;张义科[10]等以实验方法评价了溶气压力、溶气释放器结构、表面活性剂浓度等对接触区气泡直径分布的影响;王晨[11]等从溶气压力、溶气释放器结构及其个数对接触区中气泡的生成规律开展了实验研究。
然而上述仿真和实验研究均缺乏针对接触区中气泡破碎可能性的评估,因此以陈阿强[9]等的数值模拟工况为基础,结合CHEN[8]等关于最小涡尺寸的研究,针对气浮气浮池接触区中气泡聚并行为进行数值仿真,同时对忽略接触区中气泡破碎行为的正确性做出论证。
1 求解方法及设置
1.1 气液物性参数
在几何模型中设置水和空气两相,其中水作为连续分布的主相,空气作为离散分布的次相。水和空气的密度分别为998.2 kg·m-3和1.225 kg·m-3,黏度分别为1×10-3Pa·s 和1.81×10-5Pa·s,表面张力为0.072 8 N·m-1。
1.2 几何模型及网格划分
笛卡尔坐标系中的接触区三维几何模型如图 2所示,包括分离区的一部分,作为延长区,目的是确保接触区内湍流充分发展。根据几何模型设置的网格划分方案如图 3 所示,所得六面体网格数量为256 836,节点数为274 418。

图2 气浮池接触区三维几何模型示意图

图3 网格划分方案
1.3 网格无关性验证
取接触区流域中inlet_1 截面圆心(45 mm、150 mm、175 mm),对该点处不同网格尺寸条件下的气泡直径进行监测可知,采用5 mm 的网格尺寸对几何模型进行结构性网格划分可得网格无关解。气泡直径随网格尺寸的变化如图4 所示。
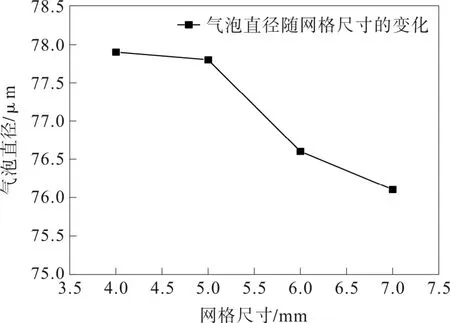
图4 气泡直径随网格尺寸的变化
1.4 边界条件设置
1.4.1 入口边界条件设置
根据文献[9]将入口1 与入口2 的流量分别设置为0.6 m3·h-1和0.3 m3·h-1,由入口1 与入口2 的几何尺寸可得流体速度分别为0.265、0.023 8 m·s-1,其中入口1 处气含率为0.038 5,气泡初始直径分布如表 1 所示。
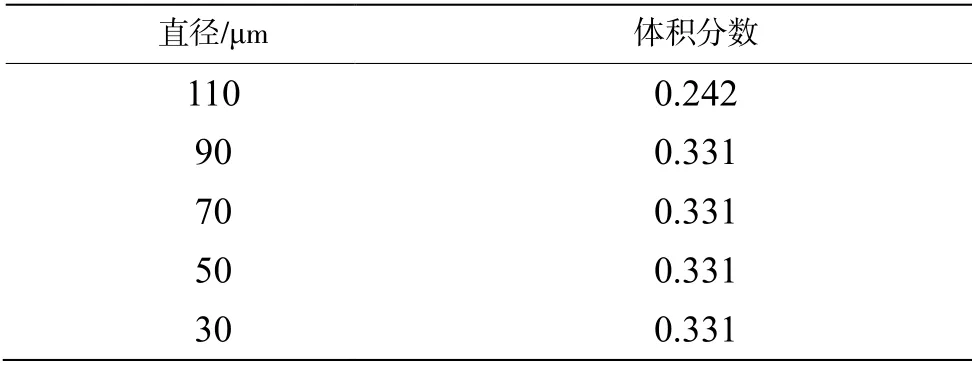
表1 气泡初始直径及其体积分数
为确保计算精确,需要得知入口1 与入口2 处的湍流强度IT。

式中:ρ—流体密度;
u—流体速度;
dv—水力直径;
μ—流体动力黏度。
对于入口2,ρ和μ应按照气液两相的体积分数加权计算,dv可依照式(2)计算,其中l和w分别为入口2 的长度和宽度。

经计算得,入口1 与入口2 处的湍流强度分别为5.48%和6.84%。
1.4.2 出口边界条件设置
气液两相流体从接触区流入气浮分离区,延长区实际上属于气浮分离区,考虑到出口处应满足流体静压强分布规律,且当流动稳定时此处湍流流动已经充分发展,因此将出口设置为outflow 边界条件。
1.4.3 液面(surface)边界条件设置
根据气浮过程中的气液两相流动特征,接触区液面处应当只允许气相溢出,故设置为degassing 边界条件。
1.4.4 壁面边界条件设置
壁面(wall)粗糙度设置为0.5。
1.5 CFD-PBM 模型设置
将气液两相流动时间设定为190 s,数值求解方法与文献[9]一致,仅考虑气浮接触区中气泡的聚并行为,故不做重复性描述。
2 数值计算结果与分析
2.1 科莫微尺度分布
湍流流场中包含许多尺寸各异的涡旋,众多湍流涡旋的运动构成湍流流动。湍流流场中的最小涡的尺寸等于科莫微尺度Kolmogorov microscale,后者可依照式(3)计算,其中ν为液相运动黏度,ε为湍能耗散率。
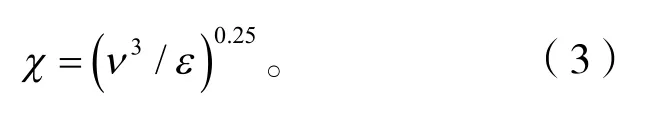
当气泡直径大于科莫微尺度时(即dbχ> )可认为气泡将发生破碎,因此使用科莫微尺度对接触区中气泡破碎行为进行评估,从而进一步验证CFD-PBM 耦合方法中忽略气泡破碎行为的正确性。不同处截面科莫微尺度分布如图5、图6 所示。
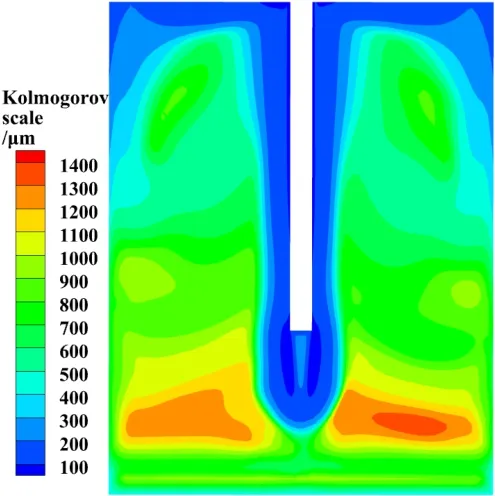
图5 流域中x=45 mm 处截面科莫微尺度分布

图6 流域中z=175 mm 处截面科莫微尺度分布
由图5 和图6 中x=45 mm、z=175 mm 处截面科莫微尺度分布可知,接触区流域中科莫微尺度的值为100~1 400 μm,绝大部分流域中的科莫微尺度的值均超过100 μm,其中大部分流域中的科莫微尺度的值均超过300 μm,考虑到流域中大多数气泡直径为70~100 μm,因此可以忽略气泡的破碎行为。
2.2 气泡直径分布和准确性验证
不同处截面气泡直径分布如图7 和图8 所示。由图7 和图8 中x=45 mm、z=175 mm 处截面气泡直径分布可知,接触区流域中的气泡直径主要分布于70~130 μm 的区间,且100~130 μm 较大直径的气泡分布于接触区上部流域,原因在于气泡上浮并在气浮区上方(参考y坐标轴方向)出现较强烈的聚并行为导致其出现较大直径的气泡。将文献[9]所示的流域中z=175 mm 处截面气泡直径分布(图9)与图8 作对比可知求解结果的正确性。
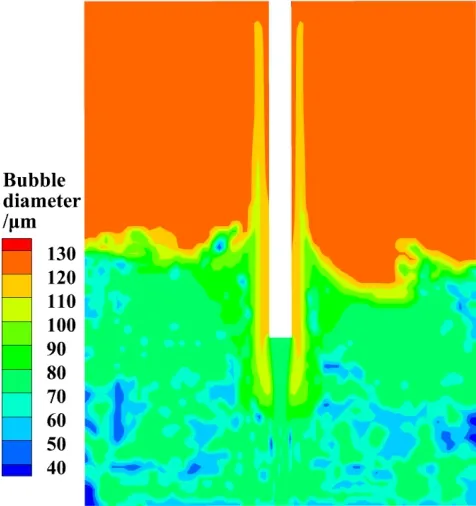
图7 流域中x=45 mm 处截面气泡直径分布
此外,图8 与图9 所示气泡在靠近接触区顶部液面处的分布规律存在差异,原因在于液面边界条件的类型与文献[9]不同。图 8 中液面附近存在明显的气泡聚集且尺寸较大,符合实际状况,而图9 中液面未体现出该现象,因此说明文献[9]当中液面边界条件有待修正。
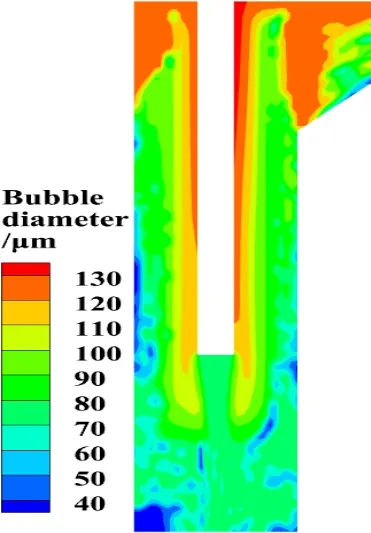
图8 流域中z=175 mm 处截面气泡直径分布

图9 流域中z=175 mm 处截面气泡直径分布[9]
3 结 论
在ANSYS Fluent 软件平台中使用CFD-PBM 耦合方法,在忽略气泡破碎行为的前提下对气浮池接触区气泡运动特性进行数值模拟研究,可得如下结论:
1)接触区流域内溶气水管出口及其外壁附近表现出相对较大的气泡直径,气泡直径的最大值为130 μm,流域中大多数气泡直径为70~100 μm。
2)接触区流域中科莫微尺度值分布于100~1 400 μm 区间,大部分流域中的科莫微尺度的值均超过300 μm,远大于流域中大多数气泡直径,因此可以忽略气泡的破碎行为。
