混合型加载下钢纤维混凝土损伤过程的声发射参数分析

宋水舟， 任会兰， 宁建国

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

0 引言

钢纤维混凝土材料在很大程度上克服了传统水泥基料抗拉强度低和韧性低的缺点，在国民基础性设施和国防工程中有着广泛的应用。长期服役过程中纤维混凝土结构可能经受地震、冲击等复杂载荷作用，其损伤破坏将经历细观尺度的微裂纹成核、扩展、汇合为特征的损伤演化，导致宏观尺度裂纹产生和扩展，最终表现为结构丧失承载能力。

载荷作用下钢纤维混凝土内损伤过程中的裂纹运动将以弹性波的形式释放出来，即产生声发射现象。如图1所示，在钢纤维混凝土损伤过程中，混凝土基体中水泥砂浆内的微裂纹、骨料破坏、骨料与砂浆交界面的裂纹，以及钢纤维运动过程中基体内的微裂纹，都会产生声发射信号。Smedt等基于端钩型钢纤维拉拔实验过程中的声发射监测结果，分析认为无论纤维分布方向如何，端钩型钢纤维运动产生声发射源的主要机制是端钩的塑性变形及伸直，其中，端钩伸直释放声发射信号的主要机理是端钩对混凝土基体造成的破坏。

图1 钢纤维混凝土中声发射来源示意图Fig.1 Schematic of AE sources in the SFRC

声发射信号及声发射参数的特征与损伤源的性质有密切关系，因此可以基于声发射参数对损伤源的性质进行表征。大量研究表明，基于声发射参数，水泥基材料损伤过程中产生的微裂纹可以分为两种类型，即拉伸型裂纹和剪切型裂纹，通过对微裂纹类型的分析，可以对水泥基材料的损伤机理进行表征，并对损伤程度及可能发生的宏观断裂模式进行预测。

当前，基于声发射对微裂纹类型进行判断的方法主要包括两种，一种是基于声发射波形的分析法，以矩张量反演法为代表，另一种是基于声发射参数的分析法，即通过上升角(RA)和平均频率(AF)的相对关系来判断微裂类型，简称RA-AF法。该方法通过一条过零点的直线(在RA-AF图上斜率为AF与RA的比值)来实现对微裂纹类型的判别。Li等在研究弯拉载荷及单轴循环压缩载荷作用下钢纤维混凝土的损伤机理时，将值分别设置为25和14。Banjara等在研究钢筋混凝土承受弯拉载荷时的损伤机理时，则将值设置为1。Ohno等比较了矩张量结果与RA-AF法所得的裂纹分类结果，并依据矩张量的结果，建议应该取值为200，一些研究以此来确定对微裂纹类型进行判断。显然，直线的斜率，即比值的选取对微裂纹类型判别具有显著的影响，但公开文献中并没有针对混凝土材料给出一种令人信服的的取值方法。

此外，以高斯混合模型方法为代表的概率统计方法在裂纹源的判别中得到了一些应用。Prem等和Farhidzadeh等运用高斯混合模型，分别对钢筋混凝土梁弯曲断裂和混凝土剪力墙在循环载荷作用下的破坏进行了研究，通过高斯概率密度云图，对主导各自研究对象破坏过程的微裂纹类型进行了评估。采用上述方法，可以对主导宏观破坏的微裂纹类型进行初步估计，但并不能得出拉伸型裂纹与剪切型裂纹的精确比值。Suthar等和 Das等运用高斯混合模型和支持向量机(SVM)研究了混凝土单轴压缩破坏和SHCC单轴拉伸破坏，给出了主导混凝土破坏的微裂纹模式。

钢纤维混凝土作为一种典型的非均质材料，水灰比、骨料粒径、钢纤维配比、复杂载荷情况等因素都会对声发射信号造成影响，因此，结合声发射信号的参数特征，采用一种更准确和有效的方法来研究混凝土类材料内声发射源机制，对纤维混凝土类结构的健康监测和损伤评价具有重要的意义。基于此，本文采用声发射技术，基于高斯混合聚类和SVM方法，对钢纤维混凝土在混合型载荷下的损伤破坏特性开展研究，揭示混合载荷下钢纤维混凝土的损伤机理。

1 实验方法

1.1 试件设计

钢纤维混凝土类结构在工程应用中常常会承受拉伸型载荷(I型)和剪切型载荷(II型)的混合作用，本文选择BDCN劈裂实验来研究钢纤维混凝土在Ⅰ-Ⅱ混合型载荷作用下的破坏。

实验所采用的混凝土基体配合比(水∶水泥∶砂∶碎石)为1∶2.5∶2.38∶5.55，其中，水泥使用42.5普通硅酸盐水泥，细骨料选用河砂，粗骨料为5～10 mm的连续级配石灰岩，钢纤维含量为60 kg/m。从外形上看，常用的钢纤维包括端钩型、波浪型及直线型，已有研究表明，单根波浪型钢纤维与混凝土基体间的粘结力最强，端钩型钢纤维次之，直线型钢纤维最弱，但端钩型钢纤维对混凝土抗断裂性能的提升效果最为显著。结合依据中国工程建设协会标准CECS13: 2009的建议，在粗骨料最大粒径为10 mm的情况下，钢纤维的长度宜大于20 mm。因此，本文选择长度为30 mm、表面不镀锌的端钩型钢纤维来制作钢纤维混凝土试件，钢纤维实物如图2所示。钢纤维的物理及力学性能参数如表1所示。

图2 钢纤维Fig.2 Steel fibers

表1 端钩型钢纤维物理及力学性能参数

钢纤维混凝土制备过程参照建工行业标准JG/T 472—2015钢纤维混凝土中建议的方法及相关经验，先将粗骨料、砂子和水泥在搅拌机中干拌2 min，之后将水分两次加入拌合物中并持续搅拌，为避免钢纤维结团，在搅拌过程中将钢纤维均匀撒布在拌合物中。均匀搅拌3 min后，将拌合物装入模具并于振动台振动2～3 min。静置24 h后脱模并放入养护室养护28 d。

试件半径=50 mm，厚度=50 mm，预制中心裂纹长度为28 mm，宽度为1 mm。为保证试件从预制裂纹尖端处起裂，并保持稳定的加载形式，在试件与压头之间加入弧形垫块，使载荷在试件表面均匀分布。为使试件将处于Ⅰ-Ⅱ混合型载荷条件下，本文选择的夹角为20°，试件及加载方法示意图如图3所示。

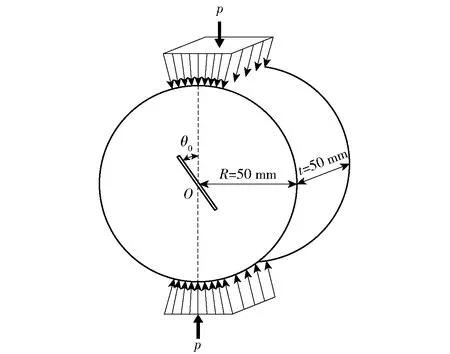
图3 加载形式Fig.3 Loading

1.2 实验方案

采用长春科新公司生产的WDW-300材料试验机对试件进行加载，通过位移控制加载，加载速度为0.05 mm/min，保持准静态加载条件直至试样破坏。

实验过程中产生的声发射信号通过美国PAC公司生产的PCI-2声发射信号采集系统进行采集。系统采样频率为1 MHz，波形长度为1 024(1 024 μs)，包含1 024个采样点，预触发长度设置为256 μs，撞击闭锁时间设置为2 000 μs。实验开始前在每个传感器附近进行5次断铅实验，以检测传感器灵敏度。依据噪声测试结果，噪声门槛设置为45 dB。传感器采用Nano30谐振式传感器，频率范围为125～750 kHz。传感器布置形式如图4所示。

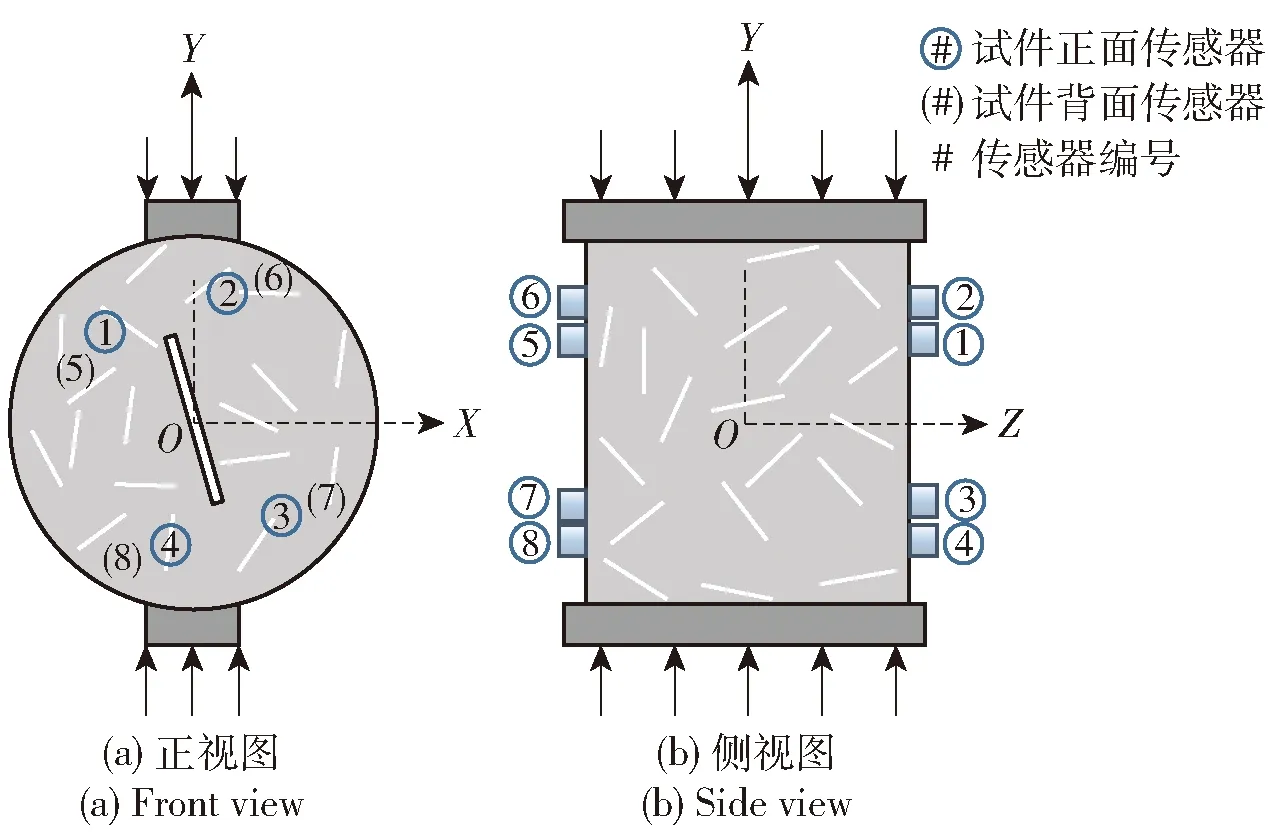
图4 声发射传感器布置形式Fig.4 AE sensor layout

加载过程中，用相机对混凝土断裂过程进行拍照记录。实验设置如图5所示。

图5 实验布置Fig.5 Experimental setup

2 分析方法

2.1 RA-AF微裂纹分类法

钢纤维混凝土破坏过程中释放的声发射信号一般为突发型。典型的突发型信号如图6所示，其中为幅值，是指波形的最大幅值，为声发射计数，是指越过门槛的波峰个数，为信号持续时间，是指从信号第1次超过门槛对应时刻到最后一次越过门槛对应时刻之间的时间间隔，为上升时间，是指信号第1次越过门槛的时刻与最大振幅对应时刻之间的时间间隔。在基本声发射参数的基础上，可以定义和。如图6所示，的定义是上升时间与幅值的比值，的定义是计数与持续时间的比值。值及可以通过(1)式和(2)式计算得到：

=

(1)

=

(2)

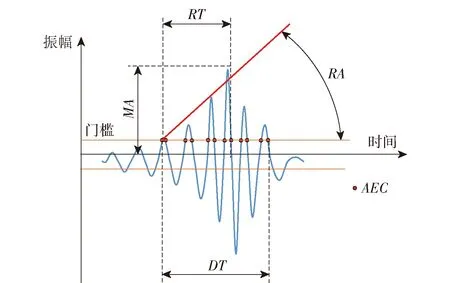
图6 典型突发型声发射信号Fig.6 A typical burst AE signal

文献[28]的研究结果表明，拉伸型裂纹具有值低值高的特点，剪切型裂纹具有值高值低的特点。因此，可以依据值和值对微裂纹的类型进行判别。据此得出的判别方法如图7所示。

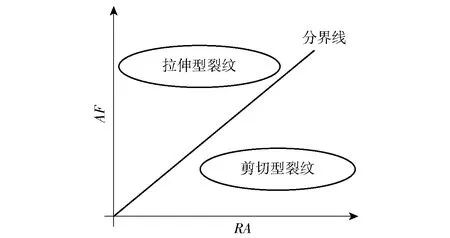
图7 微裂纹分类Fig.7 Conventional microcrack classification method

2.2 高斯混合聚类

如前所述，当前-法存在的主要问题是拉伸型裂纹与剪切型裂纹边界的不确定性。相关文献中的方法只是依据拉伸型裂纹及剪切型裂纹值及值的特点来对裂纹类型进行判断，判断结果的精确性会受到影响。而高斯混合聚类算法作为一种基于统计学知识的算法，可以依据数据分布特点对数据进行分类，划分结果可以反映数据的内部特征。

高斯混合聚类方法是一种无监督学习算法，依据数据集中样本属于各个类别的高斯概率实现对样本所属类别的划分。设数据集由类样本组成，样本总数为，每个样本用表示，其中=1, …,。的特征维度为，每个类中的样本在统计规律上都满足高斯分布，其概率密度为

(3)

式中：为维均值向量；为×阶协方差矩阵。

但是，当所有样本在样本空间中混合分布时，形成的数据集并不满足单一的高斯分布，其概率密度可以用个独立高斯分布概率密度函数的加权形式进行表示，即

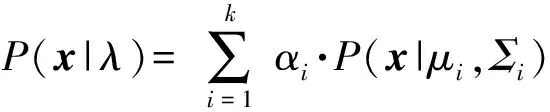
(4)

式中：为每个独立高斯分布的权重，满足

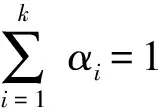
(5)

表示混合高斯密度中所有参数的合集，可以记为

=(,,)

(6)

当确定后，可以求出样本属于第个类的概率，据此将样本划入最大的一个类。

进行计算时，首先对进行初始化，之后采用期望最大化算法，对(4)式的最大化(对数)似然形式进行迭代计算。当期望最大化算法满足迭代停止条件(最大迭代次数或似然函数增长很少或不再增长)时，记录此时的及，完成对数据的分类。

如图8所示，在本文实验条件下得到的-图呈现如下特征：数据分布在两个近似椭圆的簇中。在图8中，每一个点代表一个微裂纹，因此非常适合用高斯混合聚类算法对微裂纹进行分类。

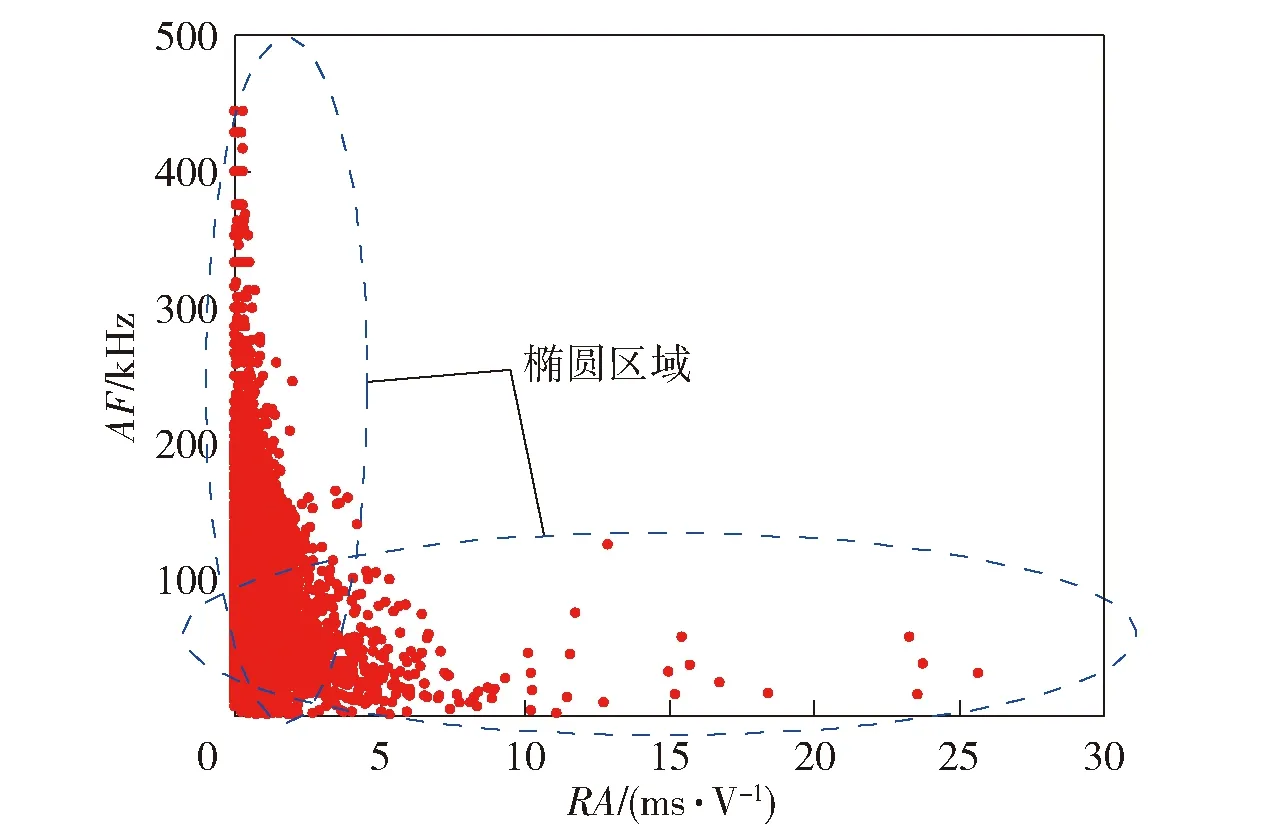
图8 数据分布形状示意图Fig.8 Diagram of data distribution

2.3 SVM理论

SVM的功能是为两类数据寻找一个合适的分界面，使两类数据能够被最完整地区分开，此时的分界面被定义为最优超平面。将数据与其标签构成一个新的向量，=(,)，对于个数据，可以构成维向量空间=(, …,, …,)。在向量空间中，超平面可以用如下方程来进行描述：

+=0

(7)

式中：为超平面法向量，用于描述超平面的方向，=(,, …,)；为超平面位移项，用于描述超平面与原点之间的距离。故可将超平面记为(,)，两类向量中距离超平面最近的几个向量被称为支持向量，两个异类支持向量到超平面的距离之和为

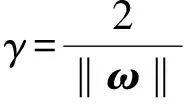
(8)

求取最优超平面，即计算和使得最大，若考虑数据线性不可分的情况，则求解的目标函数为

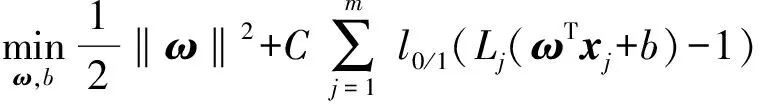
(9)

此时允许一部分点不满足约束条件：

(+)≥1,=1, 2, … ,

(10)

式中：01(·)为“01损失函数”；为一个大于0的常数，当取有限值时，允许一些数据不满足约束条件，取无穷大时，将迫使所有数据满足约束条件。

3 实验结果及讨论

3.1 损伤过程

基于声发射参数，可以对钢纤维混凝土的损伤过程进行定性描述。在众多声发射参数中，声发射幅值及累积声发射信号强度(CSS)都可以反映声发射活动的剧烈程度。两个参数已经广泛应用于对混凝土类材料损伤过程进行研究。

声发射信号强度是指持续时间范围内，声发射信号波形对时间的积分。对声发射信号强度在时间序列上累加，即可得到CSS随时间变化的曲线。

本文实验中共设置8个传感器，对于同一声发射事件，8个传感器采集到的声发射波形如图9所示。由于弹性波到各个传感器的传播距离及传播路径不同，导致波的衰减程度不同，造成采集到的信号有差异。图10给出了试件3中8个传感器测到的CSS值随时间的变化曲线。

图9 1～8号传感器记录到的波形Fig.9 Waveforms recorded by AE sensors 1-8

图10 从不同传感器计算得到的CSS值Fig.10 CSS values obtained by sensors 1-8

各传感器记录到的CSS值表现出类似的规律，因此选择任意一个传感器记录到的数据都可以对实验中钢纤维混凝土的损伤过程进行分析。本文选择5号传感器记录到的数据来对钢纤维混凝土的损伤过程进行分析。

3个试件对应的CSS曲线及声发射信号幅值分别如图11和图12所示，图12中每个点代表一个声发射信号。从图11和图12中可以看出，3个试件的载荷曲线及声发射活动整体相似。依据CSS曲线的变化情况，时间- 载荷曲线可以分为3个阶段：

1)阶段：从图11中可以看出，CSS值保持在非常低的状态，表明这一阶段中声发射活动并不强烈；图12显示该阶段内产生少量的声发射信号，幅值均在70 dB以下。

图11 CSS与载荷曲线 (5号传感器)Fig.11 Load and CSS versus time (Sensor 5)

2)阶段：如图11所示，从点对应的时刻开始，CSS值以近似线性的形式开始增长，表明此时试件内部产生的声发射信号强度较为均匀，点对应的载荷约为峰值载荷的50%～60%。图12显示，与阶段相比，这一阶段声发射信号的数量明显增多，但大多数信号幅值仍在75 dB以下。结合图13(a)观察到在试件表面预制中心裂纹尖端产生了两条宏观裂纹，而由于钢纤维发挥了对裂纹的桥接作用，这两条宏观裂纹扩展比较缓慢。因此，可以认为声发射源主要是混凝土基体内的微裂纹以及裂纹的稳定扩展。

3)阶段：由图13(b)可以看出，当载荷达到峰值(点)时，在阶段出现的宏观裂纹扩展至垫块附近，同时在垫块附近又出现一条新的宏观裂纹。由图11和图12可以看出，在这一时刻，载荷出现明显的下降，CSS值出现大幅度的突跃增长，且幅值高于70 dB的声发射信号密集出现，甚至还有一些幅值达到100 dB的信号。载荷在点突降到一定程度后呈现缓慢下降的态势，CSS值持续增大，测到的声发射信号数量也在持续增加。在这一阶段中，声发射信号的主要来源是钢纤维端钩的伸直过程造成的混凝土基体破坏以及混凝土基体中已有裂纹的扩展。

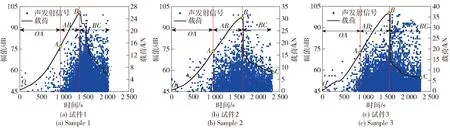
图12 声发射信号幅值与载荷曲线 (5号传感器)Fig.12 Load and AE amplitude versus time (Sensor 5)

图13 钢纤维混凝土试件3断裂过程中典型时刻试件宏观裂纹图Fig.13 Macro-cracks observed on the surface of Sample 3 at a specific time

3.2 聚类结果

为保证分析的可靠性，只选取在20 μs时间范围内被至少两个传感器采集到的信号作为分析对象，因为这些信号中的绝大多数都是来自于传感器阵列内的声发射事件。在此基础上，采用Swansong Ⅱ法对声发射信号进行滤波，以排除噪声信号的干扰。

经过滤波处理后，计算每一个声发射信号的值及值，并将一个声发射信号用向量=(,)表示。假设有个声发射信号用于分析，则可以形成维向量空间=(, …,, …,)。为将声发射信号划分为拉伸型裂纹和剪切型裂纹，将类别数设置为2。结合高斯混合聚类原理编写程序，计算每一个信号属于两个类别的概率，再结合值和值的特点，判断该信号对应的微裂纹类型。

表2中给出了试件1中阶段4个典型信号的裂纹聚类结果。信号1是该阶段中值最高的信号，信号2为该阶段中值最高的信号，信号3和4则为任意的两个信号。依据拉伸型裂纹和剪切型裂纹值和值的特点及高斯后验概率值，可以判断出信号1和信号2所属的类别分别是拉伸型裂纹和剪切型裂纹。因此，与信号1同属一个类别的信号是拉伸型裂纹，如信号3；与信号2同属一个类别的信号是剪切型裂纹，如信号4。

表2 典型信号分类结果

3个SRFC试件声发射源的聚类结果如图14～图16所示。从图14～图16中可以看出，拉伸型裂纹的值较高、值较低，剪切型裂纹的值较低、值较高。这一结果符合拉伸型裂纹及剪切型裂纹的特点。

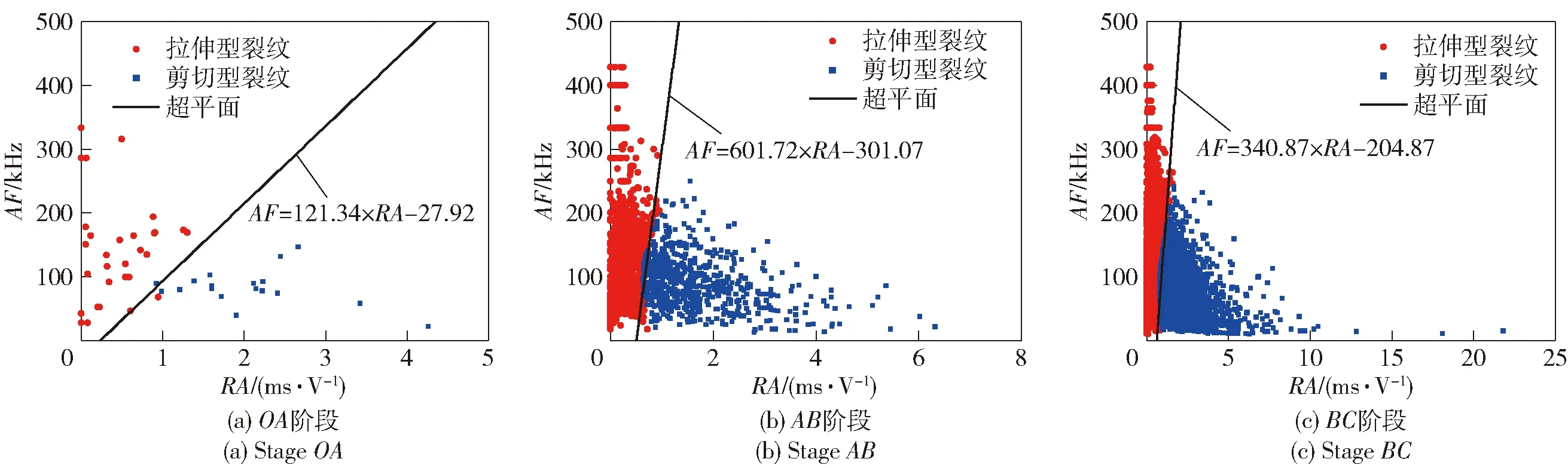
图14 试件1分阶段求超平面Fig.14 Calculation of the hyperplane for each stage in Sample 1

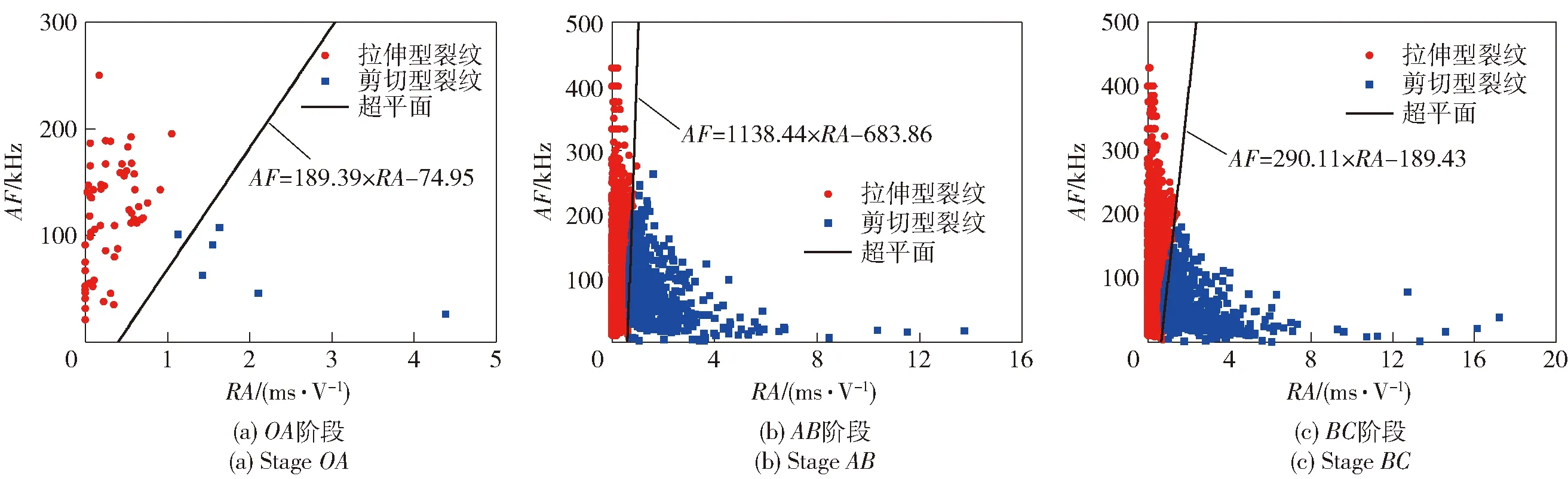
图15 试件2分阶段求超平面Fig.15 Calculation of the hyperplane for each stage in Sample 2

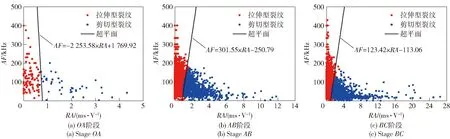
图16 试件3分阶段求超平面Fig.16 Calculation of the hyperplane for each stage in Sample 3

运用高斯混合聚类判断出裂纹的类型，可以视作对每一个裂纹赋予了一个标签，运用SVM的识别分类功能，可以求得两类裂纹的分界线，实现对拉伸型裂纹及剪切型裂纹对应-关系的定量化描述。

运用SVM，可以求出不同试件在不同损伤阶段拉伸型裂纹与剪切型裂纹之间的超平面。计算时，为兼顾计算效率与计算结果的精确性，将常数设置为10。超平面计算结果如图14～图16中直线所示，从中可以看出，不同试件、不同阶段拉伸型裂纹与剪切型裂纹的分界线并不相同。

采用交叉验证法测试超平面对两类裂纹分界线描述的准确性。

对进行分层采样，将分为10个数据量基本类似且互斥的子集，将其中9个子集的并集作为训练集，剩余的1个子集作为测试集，形成一个验证数据集，进行10次采样后可以得到10个验证数据集。计算每个验证数据集被准确分类的概率，进而可以得出验证集被准确分类的平均准确率，准确率越高，则证明该超平面对分界线方程的描述越准确。

如表3中所示，3个试件各阶段分类的平均准确率均达到95%以上，表明超平面可以用于准确描述拉伸型裂纹与剪切型裂纹的分界线，超平面的方程可以被视为拉伸型裂纹与剪切型裂纹的分界线方程。

表3 十折交叉验证结果

从图14～图16中可以看出，拉伸型裂纹与剪切型裂纹的分界线并不一定是一条过原点的直线。相关钢纤维混凝土研究直接将分界线方程设置为一条过原点的直线，而不同研究人员对分界线的斜率并不相同，有较大的随意性。本文通过机器学习算法对声发射信号数据集进行运算，进而得出了分界线方程，计算结果充分反映了数据集的数学特性，克服了文献中对比值选取的任意性，更有效地揭示了钢纤维混凝土中损伤演化的力学机理。

3.3 损伤机理

宏观裂纹是由微裂纹汇聚产生的，因此统计拉伸型裂纹及剪切型裂纹的数量，可以得出主导损伤的细观裂纹类型，进而从细观上表明混凝土的损伤机理。

分别对3个试件不同阶段拉伸型裂纹和剪切型裂纹的数量进行统计，结果如图17所示。图17中：在阶段，3个试件中的裂纹数量都较少，其中拉伸型裂纹的数量明显多于剪切型裂纹的数量，在这一阶段中，3个试件中拉伸型裂纹的占比分别为792、908和692，表明在阶段中产生的微裂纹多为拉伸型裂纹；在阶段，拉伸型裂纹和剪切型裂纹的数量都急剧增多，3个试件中拉伸型裂纹的数量分别增长到992个、1 408个和2 558个，占裂纹总数的比例分别达到648、701和679；进入阶段后，裂纹数量继续增多，试件1中裂纹数量的增多最为明显，与阶段类似，拉伸型裂纹数量占优。该阶段中拉伸型裂纹的占比分别为64、734和691。

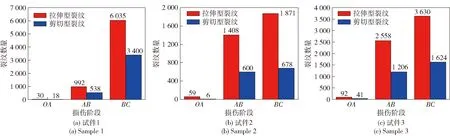
图17 各阶段裂纹数量Fig.17 Number of microcracks in each stage

钢纤维混凝土的损伤过程中既产生拉伸型裂纹又产生剪切型裂纹，拉伸型裂纹与剪切型裂纹的汇聚形成了宏观裂纹(见图13)。微裂纹数量的统计结果表明，拉伸型裂纹在数量上占优，因此在细观层面上拉伸破坏是产生损伤的主要机制。

4 结论

本文进行了带预制中心裂纹的钢纤维混凝土巴西圆盘劈裂实验，采用多通道声发射系统对试件断裂过程进行了全程监测。结合声发射参数的变化特征，基于高斯混合聚类算法和SVM方法研究了钢纤维混凝土在Ⅰ-Ⅱ混合型载荷条件下的损伤机制。得到主要结论如下：

1)依据载荷和声发射累积信号强度(CSS)随时间的变化曲线，试件损伤破坏过程中3阶段的声发射特点有：加载初期，试件微裂纹成核，产生了少量低幅值的声发射信号；裂纹稳定扩展阶段，大量较高幅值(75 dB)的声发射信号产生，CSS急剧增加；峰值载荷之后，试件内有大量高幅值(>75 dB)的声发射信号，宏观裂纹扩展汇合最终导致试件破坏。

2)采用高斯混合聚类方法，基于声发射信号的和值，将损伤过程中的声发射源划分为拉伸型裂纹和剪切型裂纹。从裂纹分类结果可知，拉伸型裂纹主导了3个阶段中混凝土的损伤演化过程，剪切型裂纹则对钢纤维混凝土的破坏起到了促进作用。

3)运用SVM方法给出了3组钢纤维混凝土试件不同损伤阶段中拉伸型裂纹与剪切型裂纹之间的超平面方程，并采用十折交叉法验证了超平面结果的准确性。由边界方程得出，拉伸裂纹和剪切两类裂纹的边界并不总是一条通过原点的直线。