基于信源数目估计的超定盲信号分离*

马 诚，李云红，陈锦妮

(西安工程大学 电子信息学院 西安 710048)

0 引 言

信源数目估计是盲信号分离算法应用的前提，也是一个技术难点[1-2]。盲信号分离[3-6]也一直是信号处理领域的研究热点，其可以根据混合信号和源信号的维数分为欠定[7]、适定[8]、超定[9]三种情况。目前，大多数盲信号分离算法属于适定盲分离[10-11]，即源信号维数与混合信号维数相等，然而在实际应用中，源信号维数往往未知且处于动态变化中，并且信号在传播过程中易受噪声的干扰，因此，信源数目准确估计的难度大幅度提高，并直接影响盲信号分离效果。

随着盲信号分离算法的发展，出现了一些性能较好的盲信号分离算法。主分量分析[12]作为其中分离性能较好的方法之一，其假定信号服从高斯分布，只考虑信号的二阶统计特性，而无法描述信号的概率分布特性。非线性主分量分析[13](Nonlinear Principle Component Analysis)方法通过在算法中添加非线性函数，使得变换后的信号服从高斯分布，因而算法实质上考虑了信号的高阶统计特性。核主分量分析方法的提出，进一步拓展了其应用范围。

目前，盲信号分离主要面临两个主要难题：一是传感器接收到的信号会受到信道噪声的影响；二是混合信号的维数不一定和源信号的维数相等。这就使得信道噪声去除和源信号维数估计显得尤为重要。因此，针对上述问题，本文提出基于信源数目估计的超定盲源信号分离方法，能有效去除信道中的噪声，并对源信号维数准确估计，实现盲信号的准确分离。

1 数据预处理

1.1 含噪数据的预白化处理

含信道噪声的盲信号分离的数学模型如下：

X(m×N)=A(m×n)·S(n×N)+ξ(m×N)。

(1)

式中：S=[s1,s2,…,sn]T为n维源信号，A是m×n维混合矩阵，ξ表示信道噪声，N代表信号样本个数，X=[x1,x2,…,xn]T表示传感器观测的m维数据向量即混合信号。

白化是有效的盲源分离预处理方法。白化不仅可以消除原数据之间的相关性，而且一定程度上可以抑制噪声。

当样本个数N足够大时，并且假定源信号S已经经过单位化处理，根据中心极限定理观测信号的协方差矩阵Σ可以表示为

Σ=AAT+ψ。

(2)

式中：Σ=XXT/N，噪声协方差矩阵ψ=ξξT/N是对角矩阵。

标准主分量分析算法用于预白化处理，当公式(1)的噪声为零时或者信噪比非常高时C-AAT应该趋近于零。根据主分量分析思想，可将AAT进行特征值分解，如公式(3)所示：

(3)

式中：Λn表示由矩阵C的前n个最大的特征值组成的对角矩阵，Un是其对应的特征向量。则有

(4)

令

z=Λn-1/2UnTX，

(5)

则有E(zzT)=In，代表z各个分量之间相互正交，即各维信号之间不相关。

对于包含信道噪声的数据，特别是当信噪比较低时，公式(2)中的噪声协方差矩阵ψ无法忽略，上述方法无法直接应用。

采用类似于标准主分量分析方法，由公式(2)可发现，C-ψ应该与AAT相等。式(2)中假定噪声协方差矩阵ψ是已知的，然而实际上噪声协方差矩阵ψ未知，因此必须估计噪声协方差矩阵。建立如下的评价函数：

J(A,ψ)=tr[AAT-(C-ψ)][AAT-(C-ψ)]T。

(6)

很显然，评价函数越小，C-ψ应该与AAT越接近。评价函数的微分为

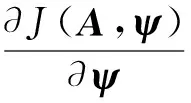
(7)

则可得到

(8)

1.2 噪声协方差矩阵的估计

设x=Af+ε，其协方差矩阵具有结构Σ=AAT+ψ。这里A是n×m阶矩阵，rank(A)=m，则A和ψ的极大似然估计满足下面的方程组：

(9)

式中：矩阵S满足

(10)

公式(9)方程组的解并不唯一，并且迭代法求解方程组时算法也有可能不收敛。Joreskog提出了一种求解方法，同时满足解的唯一性条件和算法的收敛性要求。

假设A和ψ满足唯一性条件ATψ-1A=Δ，则A和ψ的极大似然估计满足

(11)

而且tr[(AAT+ψ)S-1]=n。通过公式(11)可得到ψ的估计。

2 源信号维数估计

(12)

则变换完后新的数据为

z=Qx。

(13)

交叉验证法(Cross-validation)是多变量统计技术常用的一种方法，其基本思想是，一组数据用来提取特征，另一组数据来对数据进行验证。本文也将采用该方法对源信号的维数进行估计。

(14)

根据上述描述方法，用于噪声去除和源信号估计的方法的简要步骤如下：

Step1 根据信号X计算其协方差矩阵C，并设置噪声协方差矩阵ψ的初始值。

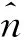
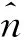
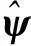
Step5 重复Step 3和Step 4，直至估计值收敛。

3 仿真实验

为了验证本文方法的性能，选择盲信号分离中常用的信噪比作为评价指标，其计算方式如式(15)所示：

(15)

3.1 轻拖尾与轻拖尾混合信号的源信号维数估计

图1是由Matlab的系统函数生成的正弦波信号，周期分别为20 s和80 s，采样点数为1 000，归一化峭度分别为-1.297和-1.521。

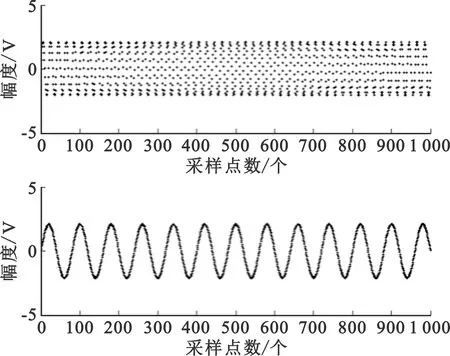
图1 源信号

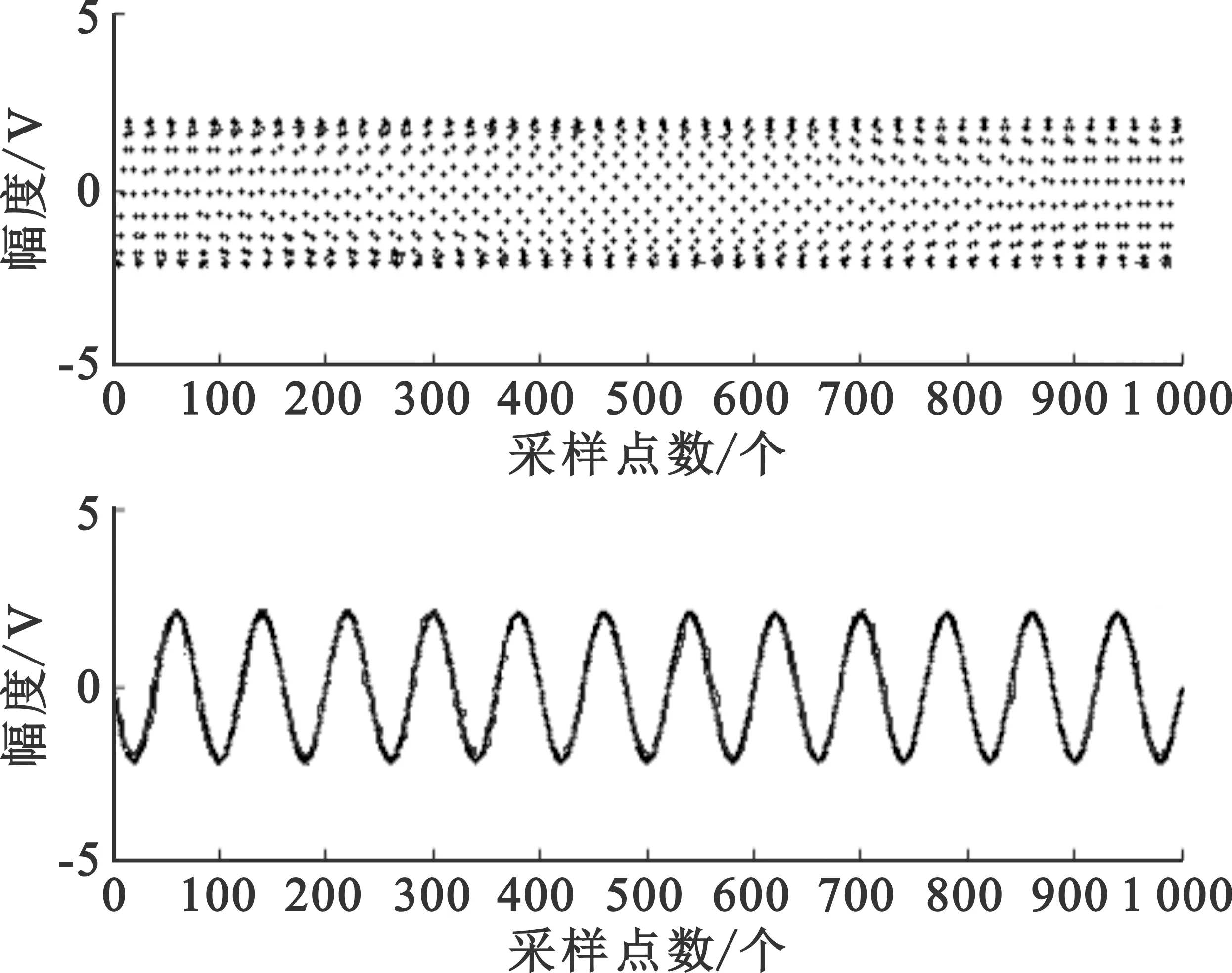
图2是线性混合后的信号。混合矩阵A服从区间[0,1]上均匀分布的6×2随机矩阵，并在信道中添加高斯噪声，信噪比为-10 dB。从图2可看出，经过线性混合之后，由于包含较强的高斯白噪声，源信号已经淹没在噪声信号中，无法看出原始信号。

图2 线性混合信号

图3 源信号维数估计

图4是针对轻拖尾与轻拖尾混合信号采用扩展最大熵、Kernel ICA与高斯混合模型三种盲信号分离算法的信号分离结果。图4(a)为扩展最大熵的信号分离效果，图4(b)为Kernel ICA的信号分离效果，图4(c)是经过数据预处理后采用基于高斯混合模型盲信号分离算法的分离结果。通过对比可看出，经过预处理后，可以很好地分离信号，并且分离信号与源信号较为接近。

(a)扩展最大熵分离信号

表1为三种方法的分离性能、运算时间的对比。从表中可知，高斯混合模型盲信号分离方法的信噪比最高，说明该方法的分离效果最好；同时，该方法运算时间也较少。

表1 三种方法分离轻拖尾与轻拖尾信号实验结果

3.2 重拖尾与轻拖尾混合信号的源信号维数估计

图5是两个正弦波信号和一段真实语音信号，三个源信号的归一化峭度分别为0.373 9、-1.297和-1.521，样本点个数为1 000个。

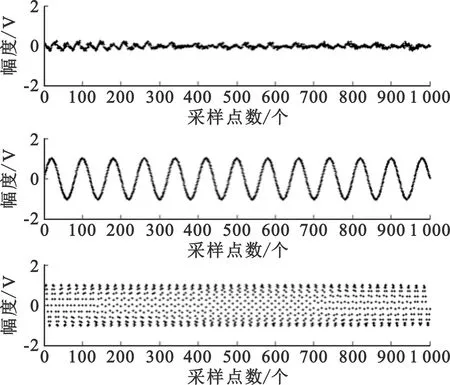
图5 源信号

图6是线性混合后的信号，混合矩阵A为服从区间[0,1]上均匀分布的6×3随机矩阵，并在信道中添加高斯噪声，信噪比为-12 dB。从图中可看出，经过混合之后，各维信号混合较为明显，已经无法看出原始信号。

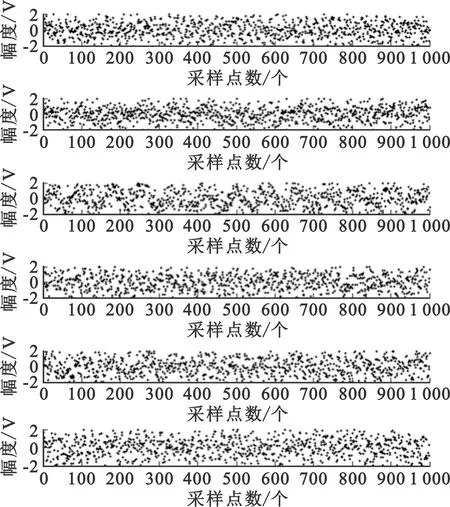
图6 线性混合信号

图7是采用本文预处理方法对源信号维数进行估计的结果，横坐标为源信号数目的估计值，范围为1～6。从图中可以看出，当估计的维数为3时误差值最小，也就是源信号的维数为3，这与真实信号数目是一致的。

图7 源信号维数估计

图8是针对重拖尾与轻拖尾混合信号采用扩展最大熵、Kernel ICA与高斯混合模型三种盲信号分离算法的信号分离结果。图8(a)为扩展最大熵对重拖尾与轻拖尾混合信号的分离效果，图8(b)为Kernel ICA的分离结果，图8(c)是经过数据预处理后采用基于高斯混合模型盲信号分离算法的分离结果。从图中可看出，采用基于高斯混合模型盲信号分离算法经过预处理后可以很好地分离信号，并且分离信号与源信号较为接近，该方法还可以有效地恢复出源信号。

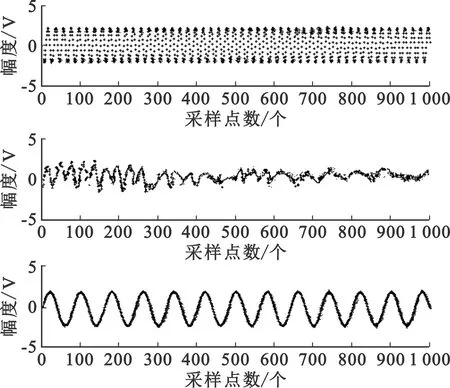
(a)扩展最大熵分离信号

表2为三种方法的实验对比结果。从运算时间和恢复效果来看，本文方法能在相对较短的时间内对信号进行有效恢复。

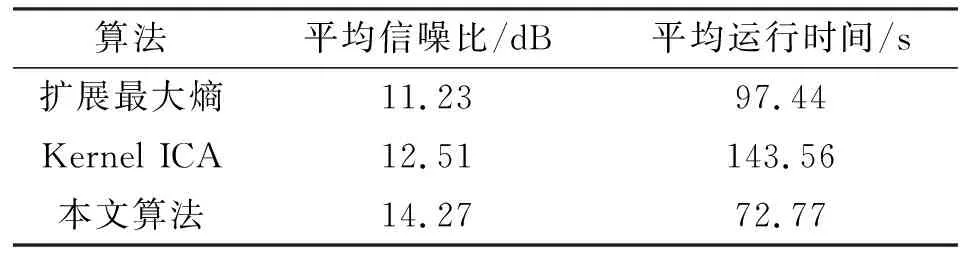
表2 三种方法对比实验性能

从两组实验的仿真结果可得出，对于多种类型的混合信号，本文提出的噪声去除和源信号维数估计方法能对源信号维数准确估计，根据估计结果可对盲信号准确分离。

4 结束语

本文提出了一种用于信道噪声去除和源信号维数估计的数据预处理方法。采用本文算法对含噪声的轻拖尾与轻拖尾、重拖尾与轻拖尾两组混合信号的源信号个数进行估计，仿真结果表明，该算法能去除信道中的噪声并准确估计盲源个数，平均信噪比增加了2.4 dB，平均运行时间提高了近50%。但是，该方法主要适合于服从高斯分布的噪声，对于其他分布类型噪声去除效果并不理想，这一点还有待进一步改进。