基于多特征SSA-ELM的调制识别*

肖 潇，谢跃雷,2

(1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；2.认知无线电与信息处理省部共建教育部重点实验室，广西 桂林 541004)

0 引 言

通信信号识别在通信电子对抗、无线电信号管理等领域有着重要的地位和作用，多年来一直是非协作通信领域共同关注的研究课题。目前，信号调制方式识别在军事和民用领域得到了广泛运用，如无线电管理、无线信号监控、认知无线电以及电子侦察、通信对抗等领域。经过几十年的发展，信号识别方法逐渐分为两类：基于极大似然的决策论方法和基于特征提取的模式识别方法[1]。

决策论方法具有优秀的识别和分选性能，但计算量过大，在实际工程应用中非常受限，而基于特征提取的识别方法具有计算复杂度低、工程效率高、对各种模型匹配的优点[2]，近年来得到了较大发展。目前常用于调制识别的特征主要有瞬时特征[3]、星座图聚类特征[4]、循环谱[5-6]等，但瞬时特征及星座图特征易受噪声干扰，循环谱特征具有噪声抑制性但计算较复杂。高阶累积量由于鲁棒性较强、适用范围广，近年来应用广泛，但仍然存在问题，如低信噪比下识别率不高、调制类型受限等。

为此，本文提出构造一个基于分数阶小波变换的特征参数与高阶累积量特征组成三维特征向量，扩大识别信号的调制类型。同时，为提高低信噪比下识别率，采用麻雀搜索算法优化极限学习机后对信号进行分类，并利用仿真数据和LabVIEW控制USRP(Universal Software Radio Peripheral)硬件平台采集数据对算法性能进行验证。

1 信号模型及高阶累积量特征

1.1 信号模型

本文所提算法属于基于特征提取的模式识别方法，整个算法结构如图1所示。

图1 调制识别算法结构图

根据图1所示，假设经信道后接收端的已调信号经载波、相位、定时同步、下变频等预处理后得到的复基带信号可表示为[7]

(1)

式中：ak为码元序列，k=1,2,…,N，N为发送码元序列长度；p(t)为码元波形；Ts为符号周期；E为平均功率；Δθ为载波相位差；n(t)为高斯白噪声。

1.2 基于高阶累积量的特征参数

高阶累积量具有一定抑制高斯噪声的特性且比高阶矩更适合用作随机信号的高阶统计应用，因此常应用于信号识别领域。对于上述信号x(t)，其p阶混合矩为

Mpq=E[x(t)p-qx*(t)q]。

(2)

式中：x*(t)表示函数x(t)的共轭，p为阶数，q为共轭位置。

根据Mpq可定义x(t)的各阶累积量表达式为

C20=Cum(x,x)=M20，

(3)

C21=Cum(x,x*)=M21，

(4)

(5)

(6)

C63=Cum(x,x,x,x*,x*,x*)=

(7)

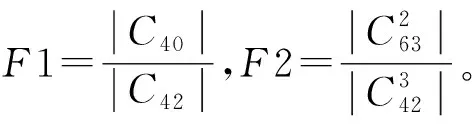
由于MFSK及8PSK、2ASK和2PSK的各阶累积量均相同，无法利用高阶累积量进行分类，故本文提出对信号进行分数阶小波变换后构造一新的特征参数。

2 基于分数阶小波变换的特征参数

分数阶小波变换(Fractional Wavelet Transform,FRWT)将传统小波变换时间-频率域分析方法推广至时间-分数域，可体现信号时间-分数域的局部化特征[9]。本文基于分数阶小波变换构造的特征参数，其计算步骤如下：

Step1对信号x(t)进行功率归一化后计算其分数阶傅里叶变换：

(8)

式中：Xp(u)表示分数阶傅里叶变换函数;p为变换阶次;变量u为分数阶频率;Kp(t,u)为变换核函数,

(9)

式中：n为自然数取值，δ(t)表示冲激函数。

Step2 对式(9)计算其分数阶小波变换：

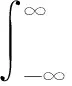
(10)

φp;v,τ(u)有如下定义：

(11)

式中：α为分数域和时域的夹角；p为变换阶次；v和τ分别为尺度因子和时移因子。

Step3 构造特征值。经过分数阶小波变换后得到小波系数S，若其长度为L，则其细节分量为

(12)

式中：{h0,h1,…,hN}为分数阶小波变换的低通滤波器系数，dm为分解水平为m的细节分量。设分解层数为N，特征参数构造如下所示：

(13)

3 基于麻雀搜索算法优化的极限学习机

极限学习机(Extreme Learning Machine,ELM)是Huang等人[10]提出的一种机器学习系统，由于其输入层权值ω和隐含层阈值b是随机初始化设置的，无需多次迭代来调整权值参数，具有训练时间短、计算量小的优点，但缩小计算量的同时也带来一些弊端——当训练样本中存在若干偏差较大的样本时，会造成矩阵病态[11]，影响网络分类性能。

针对ELM网络存在的问题，本文采用麻雀搜索算法(Sparrow Search Algorithm,SSA)对ELM进行参数优化。SSA是2020年由Xue[12]等人提出的新型群智能优化算法。首先设置适应度函数如下：

fitness=arg min(TrainErrorRate+TestErrorRate)。

(14)

适应度函数设计为追求训练集错误率与测试集错误率和的最小值。根据适应度函数，SSA算法的优化流程如图2所示。

图2 SSA算法优化流程图

SSA算法具体步骤如下：

Step1 设置SSA种群数量为20，种群中个体是待优化参数，即ELM的输入权值和隐含层阈值，初始化种群随机分为发现者及追随者。

Step2 根据适应度函数计算初始适应度值并评估，保留最优适应度值。

Step3 计算预警值，根据式(15)更新发现者位置：

(15)

Step4 发现者位置更新后，跟随者位置根据式(16)进行调整：

(16)

Step5 随机选择警戒者并发出警戒，种群做出反捕食行为，如下式所示：

(17)

式中：Xbest为当前全局最优位置；β为服从均值为0、方差为1的正态分布随机数，是步长控制参数；K∈[-1,1]随机数，表示麻雀移动方向同时也是步长控制参数；ε为最小常数避免分母为0；fg和fw分别为当前全局最优和最差的适应度值。

Step6 经过式(15)～(17)的位置更新后，计算当前种群个体的适应度值，并与原来的最优值进行比较，更新全局最优信息。

Step7 判断是否达到最大迭代次数(本文设置为50)，满足则停止迭代得到SSA-ELM网络，反之则重复Step 2～6。

4 基于多特征SSA-ELM的调制识别算法流程

基于多特征SSA-ELM的调制识别算法步骤如下：

Step1 对每类信号进行功率归一化后计算其基于高阶累积量的特征参数F1、F2和基于分数阶小波变换的特征参数F3。

Step2 将所提取的特征组成维数为3的特征向量F=[F1,F2,F3]T，并分为训练集及测试集。

Step3 利用SSA算法对ELM进行参数优化，得到SSA-ELM。

Step4 将训练集输入SSA-ELM进行训练。

Step5 将测试集输入训练好的SSA-ELM分类器，得到最终分类结果。

5 算法验证及仿真

5.1 特征参数仿真

算法所研究的调制类型共10种，分别为2ASK、4ASK、2PSK、4PSK、8PSK、2FSK、4FSK、8FSK、16QAM和32QAM，将信号在-4～20 dB带内信噪比范围内每隔2 dB进行100次蒙特卡洛仿真，其中载波频率为4 kHz，采样频率16 kHz，符号速率为2 000 b/s，噪声为高斯白噪声。根据式(10)～(13)可知，基于分数阶小波变换的特征值F3的主要参数为变换阶次p、小波基函数和分解层数N，经多次实验，设置变换阶次p=1，N=7，小波基函数为Haar小波，得到特征参数值随信噪比变化曲线，如图3所示。

(a)特征参数F1随信噪比变化曲线

由图3可知，F1可把10种信号分成2PSK、4PSK、2ASK、4ASK、16QAM和MFSK、8PSK两类以及32QAM信号，F2对4PSK、16QAM和4ASK有较好区分度，最后利用F3完成剩余信号分类。通过图3变化曲线可知，各信号间的特征值区别明显，且具有一定抗噪性，尤其是特征参数F3，即使在-4 dB时依然对信号有较大区分度。这是由于本文采用每层分数阶小波变换细节分量的最大模值进行求和来构造特征值，最大值的选取使得该特征可滤除大量信号的噪声干扰。

5.2 识别率仿真

训练集及测试集样本的带内信噪比范围为-10～20 dB且每隔2 dB产生300组信号并提取特征，其中200组作为SSA-ELM网络训练集，100组为测试集，得到各信号在信噪比为-4 dB、0 dB、4 dB、6 dB下的识别率混淆矩阵如图4所示。

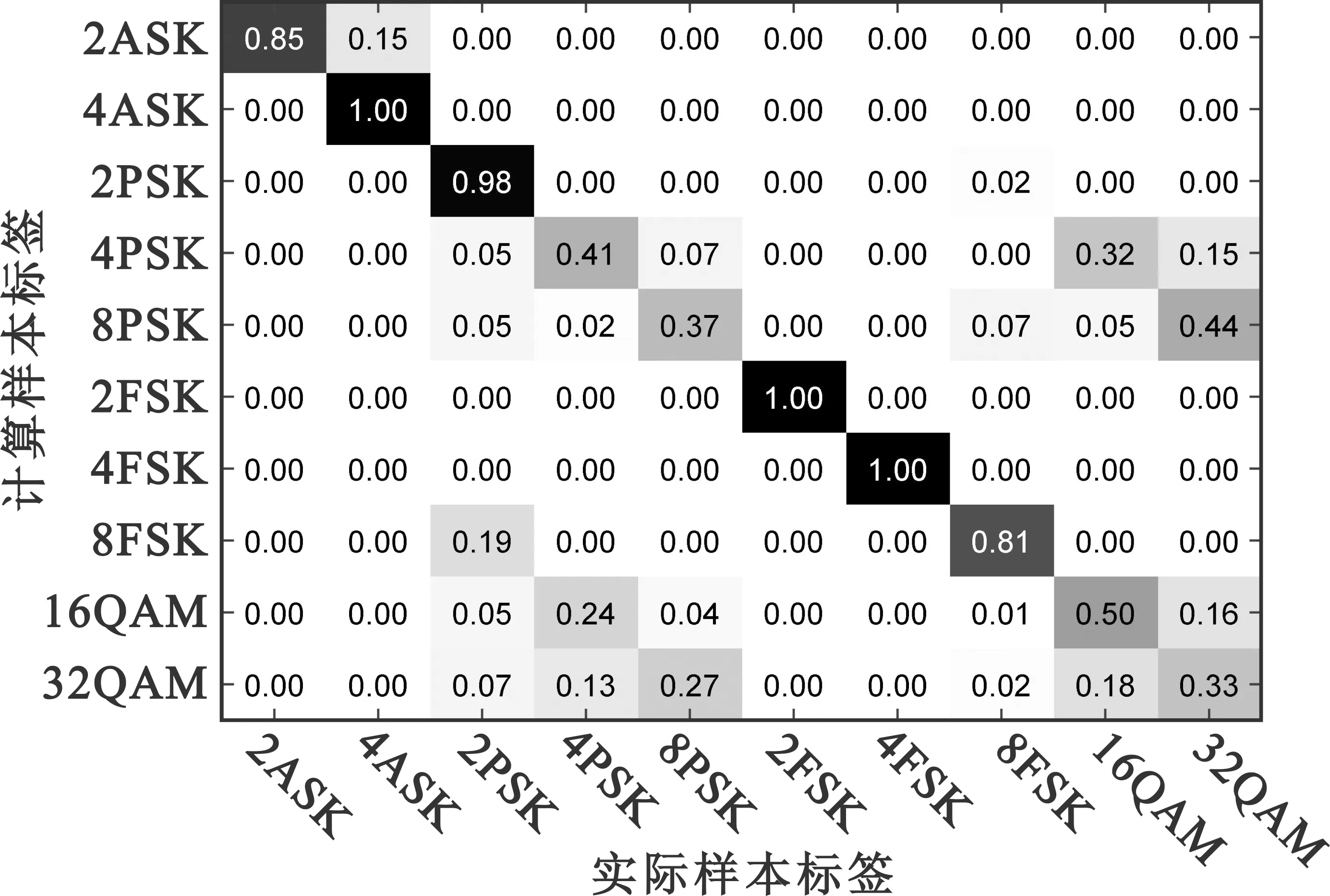
(a)-4 dB时混淆矩阵

由图4可知，在SNR为-4 dB时，4PSK、8PSK、16QAM及32QAM这四种信号受信噪比影响较大，同时也有部分2ASK信号被误识别为4ASK信号、8FSK信号被误识别为2PSK信号的情况，而SNR为0 dB时，除16QAM和32QAM的误识别率仍较高以外，其余信号均有明显提高，在信噪比达到4 dB后，16QAM及32QAM信号识别率分别为94%和87%。由上述分析可知，本文算法对16QAM和32QAM的识别性能不及其他信号，但如图4(d)所示，在SNR≥6 dB时，所有信号识别率均达到98%以上。

5.3 性能对比

图5所示为本文算法与文献[7]、文献[13]及文献[14]方法的识别率性能对比，其中文献[13]中针对MFSK信号与8PSK信号累积量相同的问题选择对其进行微分后提取累积量特征，文献[7]同样仅使用3个特征参数完成了10种信号的分类，文献[14]将MFSK信号进行傅里叶变换转到频域再提取高阶累积量特征。同时为研究SSA优化算法对于ELM网络性能的提升效果，利用训练样本分别输入SSA-ELM及ELM网络，并用相同测试集进行测试，结果如图5所示。

图5 不同信噪比下各方法识别率对比

由图5可知，本文算法的抗噪性能最为突出，在信噪比为4 dB时本文算法的综合识别率已达98%以上，而其他三种方法在4 dB时的识别率分别为92.3%、76.8%和63.4%，在信噪比小于4 dB情况下差距更加明显。通过ELM方法识别率曲线可看出，即使是未经优化的ELM网络在信噪比低于-2 dB时识别率也较高，而其他三篇文献所提方法都是利用高阶累积量特征结合其他特征参数进行识别，说明本文所提取的基于分数阶小波变换的特征参数鲁棒性强，即使在低信噪比下也有较好识别效果，且经SSA算法优化后的ELM网络性能有了明显提高。

在优化算法方面，文献[15]和文献[16]都进行了参数优化，所使用的是较为经典的遗传算法(Genetic Algorithm,GA)。图6为迭代次数为50次的SSA-ELM网络识别率与迭代次数为50和100次的GA-ELM网络的识别率对比，可看出迭代次数为50次时，整体上GA-ELM网络识别率都低于SSA-ELM，两者在SNR为6 dB时识别率都接近100%；当迭代次数为100次时，在信噪比大于-6 dB后GA-ELM的性能有了大幅度提高，甚至在2 dB时已经略微超过本文方法，但低信噪比下仍不及SSA-ELM。

图6 不同信噪比下各网络识别率对比

在相同训练与测试集条件下，使用CPU为i5-9500、内存8 GB的电脑记录以上3种情况的运行时间，结果如表1所示。经50次迭代优化的GA-ELM网络所用时间少于相同迭代次数的SSA-ELM，这说明GA算法单次迭代的计算量较少，花费时间短，但其寻优能力不如SSA算法，若想继续提高GA-ELM网络的分类性能，需要增加迭代次数，但100次迭代所用时间已经超过了SSA算法。这说明了本文所用的较为新颖的SSA算法与传统GA算法相比具有寻优能力强、优化速度快等优点。

表1 运行时间对比

5.4 基于USRP采集数据的验证

为验证算法在工程实践中的可行性，本文利用LabVIEW控制USRP硬件平台进行信号的收发，模拟现实电磁空间的信号数据，以该数据作为算法验证的数据源更具有实际工程应用参考价值。由LabVIEW软件产生同仿真数据相同的10种调制信号，硬件平台为USRP2954，在定时同步条件下设置信号载波频率为915 MHz，符号速率为62.5 kb/s，对每个码元进行8倍过采样，IQ采样速率为500 kHz，硬件采集环境如图7所示。

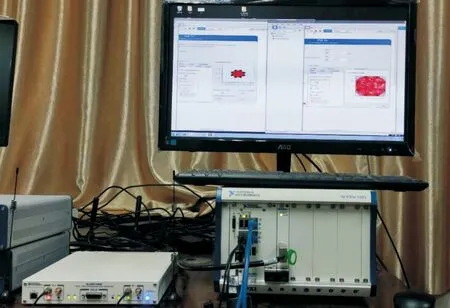
图7 硬件采集环境图

将采集数据的I、Q两路各提取1 024个采样点作为信号序列，并在实测数据的基础上添加高斯白噪声，带内信噪比范围为[-10∶2∶20] dB，每类信号在每个信噪比下共生成200组样本，按1∶1的比例分为训练集和测试集，分别输入SSA-ELM和ELM网络，得到基于USRP采集数据的识别性能曲线，如图8所示。

图8 基于采集数据的识别性能曲线

通过使用采集数据对本文算法进行验证，说明了本文算法所提的特征参数对于实测信号的适用性较好。由于硬件采集数据过程中会受到实际电磁环境干扰及硬件性能影响，基于硬件采集数据的识别结果未能接近100%的识别率，但在SNR等于6 dB时两种方法识别率均达到90%，且最高识别率达到94%，证明了本文算法的有效性。

6 结束语

本文提出了一种基于多特征SSA-ELM的信号调制识别方法，将信号进行分数阶小波变换后构造一种新的特征参数，与传统高阶累积量进行结合，采用SSA-ELM网络进行分类，实现了仅用3个特征参数就完成对调制集{2ASK、4ASK、2PSK、4PSK、8PSK、2FSK、4FSK、8FSK、16QAM、32QAM}10种信号的分类识别。经仿真及USRP硬件平台采集数据的验证，所提特征区分度高、鲁棒性强，且SSA算法与传统优化算法相比具有良好的寻优能力，优化所得SSA-ELM网络分类性能得到大幅提高，在低信噪比下效果尤为明显。

本文只研究了高斯白噪声情况下的算法性能，后续可考虑衰落信道等更加复杂的信道环境，并研究工程实现。