弹性高超声速飞行器可调Tube-MPC容错控制

米涵芃，胡超芳，杨晓荷，胡永太

1.天津大学，天津 300072

2.航空工业西安飞行自动控制研究所 飞行控制航空科技重点实验室，陕西 西安 710065

高超声速飞行器具有飞行速度快、生存力高以及灵活性强等优点，近年来逐渐成为各国发展的重点[1-2]。但其强非线性、强耦合性[3]、快时变以及不确定性等特点，为控制系统的设计带来了极大的挑战[4]。同时，由于飞行环境复杂多变和硬件限制，飞行器还要面临执行器故障[5]与输入饱和[6]等问题。除此之外，高速飞行时气动热会导致飞行器结构发生形变[7]，降低机体固有频率，激发弹性模态，从而影响飞行器的气动力和飞行状态[8]。因此，设计有效的控制策略，保证飞行器稳定飞行，具有十分重大的研究意义。

反馈线性化通过状态或输入输出的变换与反馈，处理系统中的非线性部分，从而得到期望的线性系统，是解决高超声速飞行器模型非线性问题的有效手段，受到诸多学者的青睐。如Ding 等[9]基于反馈线性化技术，针对弹性高超声速飞行器，提出了一种连续滑模控制器。An等[10]研究了一类反馈线性化系统，用于研究外部扰动和输入受限下的抗饱和控制问题。Yang等[11]通过反馈线性化将存在参数不确定的纵向非线性模型，转化为带有附加扰动的线性参变模型，并设计了预测控制器。

针对输入饱和问题，通常是研究实际输入受限下的抗饱和方法。如Chen等[12]利用双曲正切函数，解决了高超声速飞行器在再入阶段的舵偏角输入饱和问题。Xia 等[13]提出了基于积分滑模和自适应动态规划的控制律，以处理舵偏角输入饱和。但对于反馈线性化模型，实际控制输入约束会在线性化过程中转换为与状态相关非线性函数形式的虚拟输入约束，这就给控制器的设计带来了挑战。

基于以上问题，本文针对弹性高超声速飞行器反馈线性化后具有的状态依赖输入饱和特性，提出了一种基于可调Tube 预测控制（Tube-MPC）的容错控制方法。首先，采用反馈线性化建立多胞线性参变模型。其次，对于执行器卡死或随机漂移故障，在传统Tube-MPC基础上，引入了调节因子，改变鲁棒正不变集大小，以降低保守性，实现系统控制性能和鲁棒性的折中。对于状态依赖输入饱和，将标称控制律设计为凸组合形式。同时利用平方和（SOS）技术，将多项式形式的虚拟输入约束转换为线性矩阵不等式，进行控制律求解。最后，进行了仿真验证。

1 弹性高超声速飞行器模型

1.1 纵向动力学模型

本文所使用的纵向弹性高超声速飞行器动力学模型[14]如下

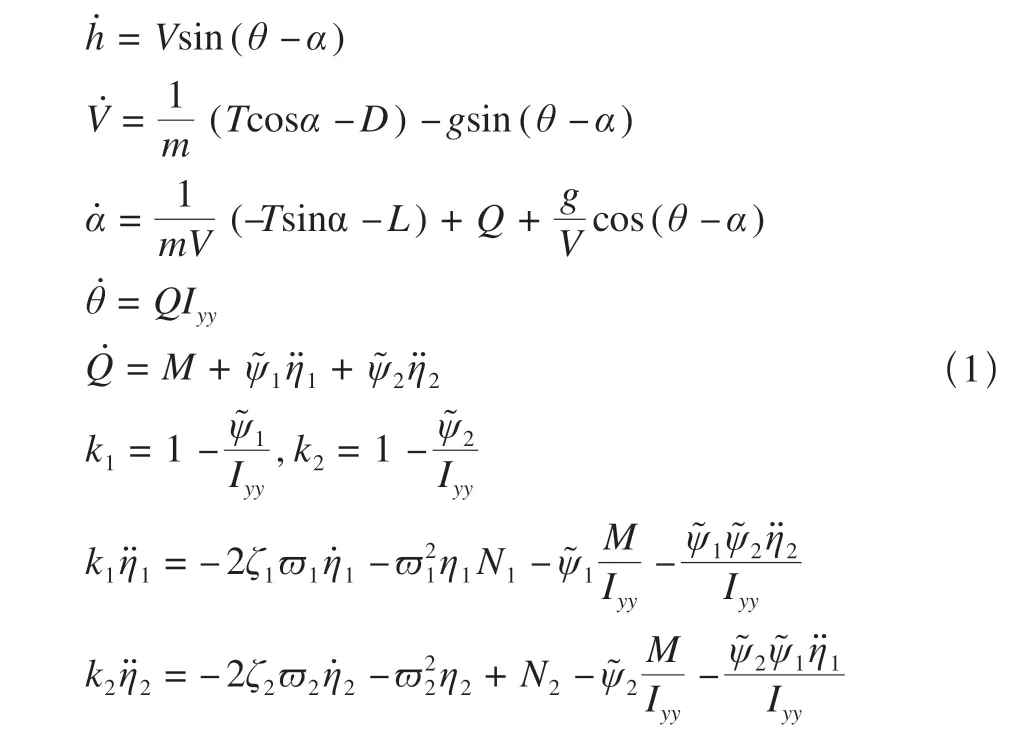
式中：飞行状态h,V,α,θ,Q,η1,2分别为飞行高度、速度、迎角、俯仰角、俯仰率和一、二阶弹性模态。m为飞行器的质量，g为重力加速度，Iyy为转动惯量。L,D,T,M,N1,2为升力、阻力、推力、俯仰力矩和弹性模态广义力。ϖ1,2为弹性模态自然振荡频率，ζ1,2为弹性模态阻尼。ψ͂1,2为约束梁耦合常数。

考虑刚体、弹性、气动系统、推进系统互相耦合，气动参数表示如下式

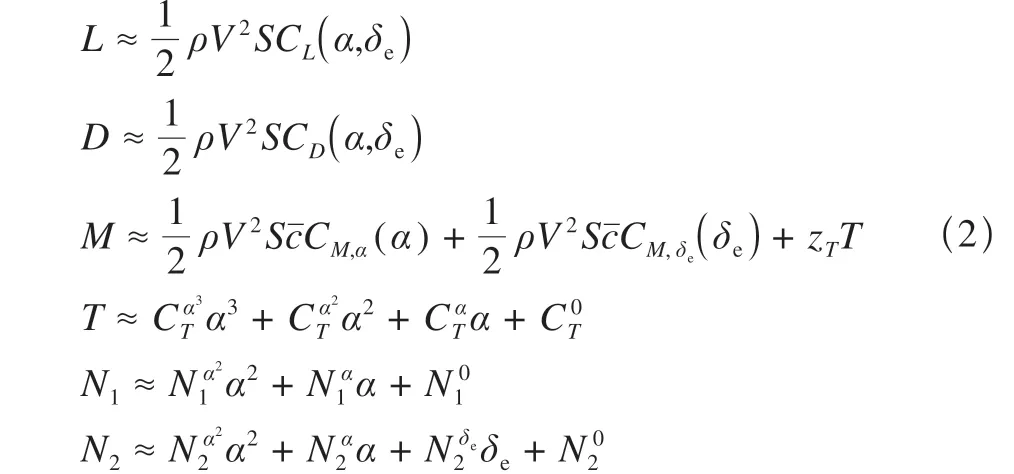
中：ρ为空气密度，S为参考面积，zT为推力力矩耦合系数，cˉ为平均气动弦长，δe为升降舵偏转角。CL,CD,CM,CT,N1,2为气动参数的拟合系数。二阶发动机系统模型如下

式中：Φ为空气当量比，Φc为空气当量比控制量，ϖe为发动机自然频率，ξ为发动机阻尼比。

1.2 反馈线性化模型

式中：A,B分别为状态矩阵和输入矩阵。

进而可以得到标称系统模型如下

以及参考点处的飞行器模型如下

考虑参数不确定，将式（4）转换为如下等效线性形式

式中：B(ΔB(t)),Bω((t)),ω(t)为由参数矩阵构成的仿射形式矩阵与矢量。

1.3 故障模型

当执行器发生失效或随机漂移故障时，实际输入变为如下

式中：ρl为执行器的有效系数，Δδe(t)为故障舵随时间变化的随机漂移量。将式（7）转换为有执行器故障和参数不确定的线性模型

式中：f为故障附加等效项，即

式中：N0(x,p0)为与实际状态和标称参数相关的矩阵。

2 状态依赖输入饱和

在实际飞行过程中，受限于执行器的具体物理结构，控制输入u=[δe,Φc]T的变化范围是有限的，其中包括舵面饱和限制和空气当量比控制量限制。具体形式如下

式中：umin,umax分别为实际输入的上下限。

由此得到虚拟控制输入的饱和函数形式如下

式中：vmin,vmax分别为虚拟输入的上下限，其具体形式如下

式中：p0为飞行器模型的标称参数，x=[h*,V*,h,V,α,θ,Q,Φ，]T为飞行状态，M0(x,p0)同样为标称参数下与实际状态相关的矩阵。

可见虚拟输入的上下限是与实际飞行状态相关的非线性函数，为了简化计算，将其拟合成关于状态误差的线性多项式。首先构建状态误差，将式(5)与模型(6)相减，并进行离散化可得到

式中：状态误差ze1与输入误差ve1形式如下

ze1(k)=z0(k)-zm

ve1(k)=v0(k)-vm

拟合后的虚拟输入上下限如下

式中：κ0∈R2×1,κ1∈R2×9为拟合系数。

因此，虚拟输入饱和可表示如下

3 Tube-MPC控制器设计

为使实际系统跟踪上标称系统，还需要构建实际系统与标称系统的误差模型。将模型(9)与模型(5)相减，离散化可得误差模型如下

式中：d=B′ω(Δω(k))ω(k) +f∈W为由参数不确定和故障转化而来的有界附加扰动，W为扰动集，B′ω(Δω(k))为由参数矩阵构成的仿射形式矩阵，状态误差与输入误差形式如下

ze2(k) =z(k) -z0(k)

ve2(k) =v(k) -v0(k)

传统的Tube-MPC控制律形式如下

式中：K为Tube-MPC的辅助反馈控制律，F为标称控制律。

本文在传统方法基础上，引入调节因子，通过调节实现控制性能和鲁棒性折中。同时，将标称控制律构造为无约束的标称控制律与约束下控制律的凸组合形式。具体设计过程如下。

3.1 辅助反馈控制律设计

定义矩阵Qm,Qn，通过求解以下线性矩阵不等式可以求得辅助鲁棒反馈控制律K=QmQ-1n。

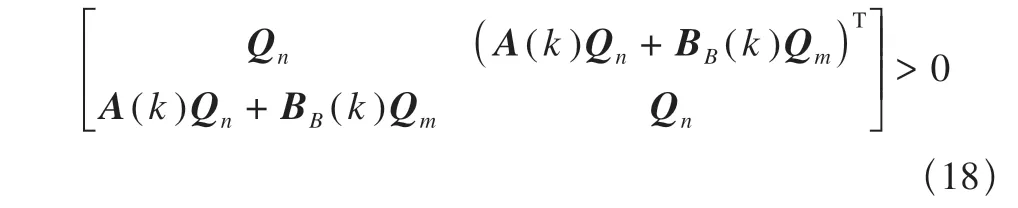
3.2 调节因子

在传统Tube-MPC 控制中，利用最小鲁棒正不变集Z来表示“Tube”的大小。为保证控制器的稳定性，通常会针对故障最严重的情况来设计控制律，但这会导致控制器的保守性过强，从而降低控制性能。考虑到实际飞行中不一定发生最坏情况，可以适当降低系统鲁棒性，以提高控制性能。因此，不必使用完全故障情况下扰动集W所对应的Z。

基于上述思想，本文借鉴参考文献[16]的思想，引入了调节因子τ∈[0,1]，用于调节不变集的大小。当故障并非完全发生时，即W变为不完备扰动集W′时，由于不变集与所发生的故障程度成正比，通过改变τ，可以将Z变为不完备扰动最小鲁棒正不变集Z′。由于τ的引入，不变集的各个维度以一定的比率缩减，因此两种不变集的关系可表示为Z′=τZ。

为简化起见，在本文中我们假设W和Z在每一个维度都缩小同样的比率，因此τ可以取一个定值。为了有效求解对应于W′的Z′，采用参考文献[17]的方法进行计算。

由此，引入调节因子的控制律如下

接下来分析τ对控制性能和鲁棒性的影响。传统Tube-MPC的标称控制律要满足

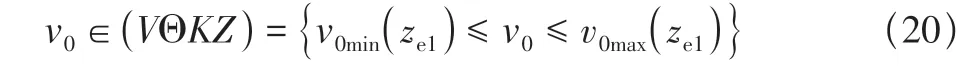
式中：Θ为集差，v0min,v0max为标称虚拟输入的上下限。

引入τ后约束条件则变为

式中：v′0min,v′0max为经τ调节后的上下限。

可见τ的引入扩大了标称控制输入约束范围。随着τ减小，标称系统约束放松，控制性能变好，而鲁棒性则变差。反之，随着τ增大，标称系统约束变严格，控制性能降低，但系统的鲁棒性会有所提升。

3.3 标称控制律设计

本文设计的标称控制律为

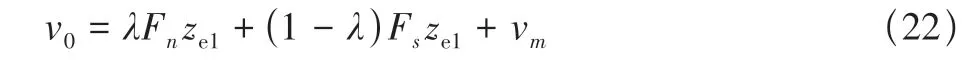
式中：Fn,Fs为无约束和约束下的标称控制律，λ∈[0,1]为权重系数。

在求解标称控制律时，需要考虑输入饱和问题，从式（15）中可以看出，M0,N0是复杂非线性函数，而且vmin,vmax是多项式形式，这使得饱和约束难以求解。因此考虑到SOS技术处理多项式约束的优势，引入SOS 将上述多项式转化为线性矩阵不等式约束，以便于控制律的求解。

定义1[18]

针对多项式H(x)，假设它可以表示为如下一组多项式gi(x),i= 1,…,m平方和的形式。

则H(x)∈∑[x]就是SOS 多项式，其中∑[x]为SOS多项式集合，且H(x)≥0,∀x∈Rn。

对于带有状态依赖输入约束的误差系统(13)，给定合适的系统状态权重矩阵ψ∈R9×9，控制输入权重矩阵σ∈R2×2，约束控制下影响不变集的参数κ∈R9×9。如果存在正标量γn，正定对称矩阵Ys和Yn，可以使辅助SOS 多项式s1(ze1(k)),s2(ze1(k)),s3(ze1(k)),s4(ze1(k))满足以下优化问题，则本文所设计的标称增益Fs=YsQ-1,Fn=YnQ-1可以保证误差系统(13)的稳定。

式中：*代表线性矩阵不等式中对称的部分，其余部分如下

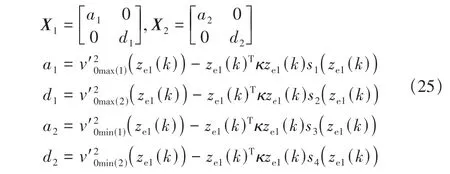
由此，可以求得虚拟控制律，经过式（26）转换后可得到实际控制输入如下

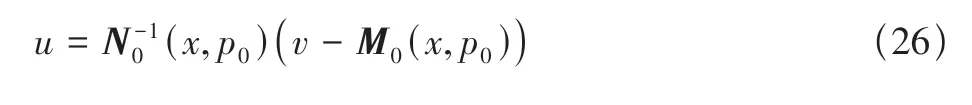
4 仿真验证与分析

仿真条件：初始高度为25908m，初始速度为2347m/s，期望高度为29184.6m，期望速度为3017.5m。故障在350s时发生，为10%失效故障。为验证本方法的有效性，与传统Tube-MPC控制器进行对比。

首先，选取τ= 1，即不引入调节因子，仅对控制器的容错以及抗饱和能力进行验证，仿真结果如图1和图2所示。

图1 飞行状态Fig.1 Flight states

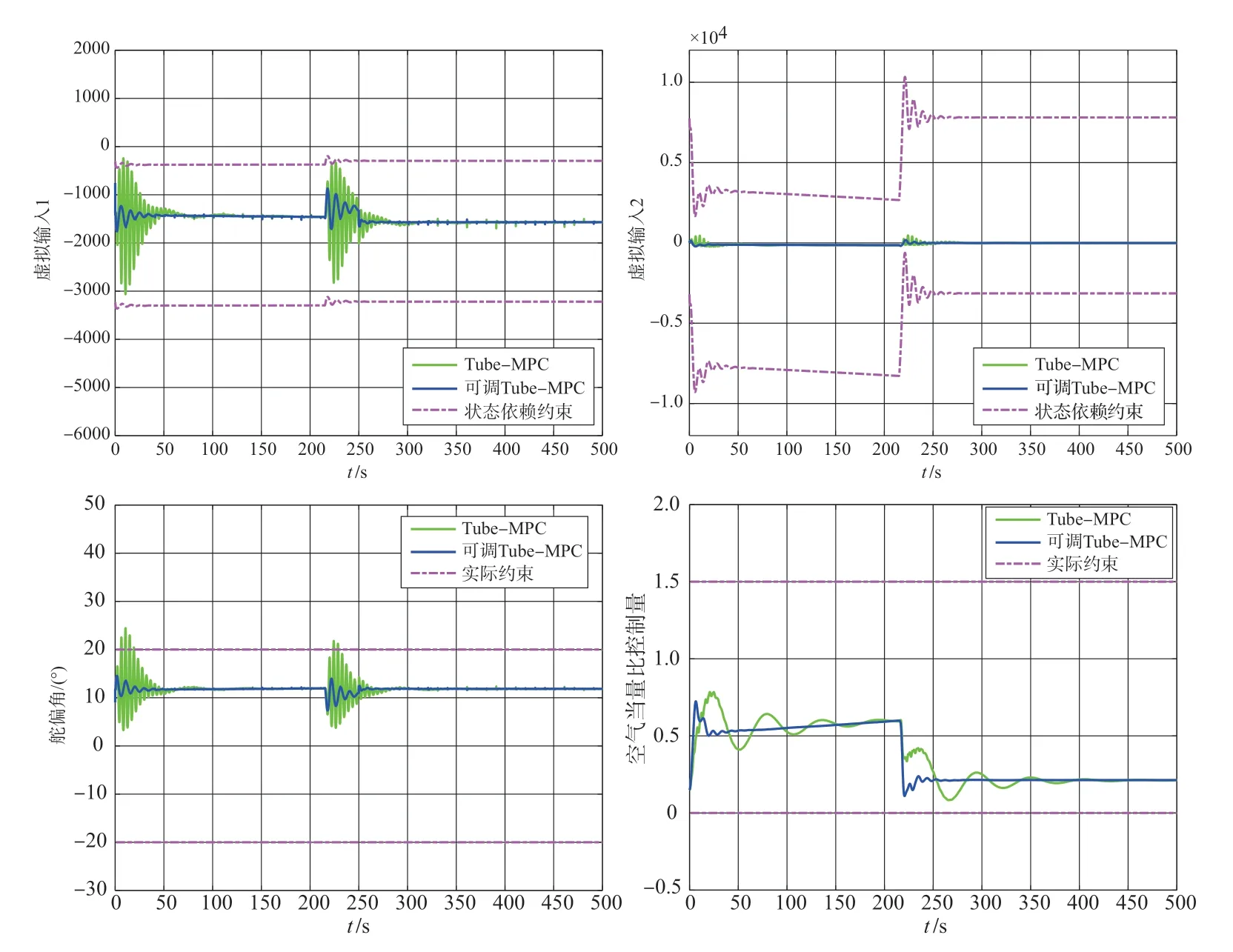
图2 控制输入Fig.2 Control inputs

由图1 可知，本方法能使弹性高超声速飞行器在故障发生时，精确完成跟踪任务。由图2可知，虚拟和实际控制输入均在约束范围内。在相同仿真条件下，分别选取τ为1和0.7进行仿真，仿真结果如图3～图5所示。由图3～图5可知，减小调节因子至0.7后，与调节因子为1时相比，系统的响应速度变快，超调量减小，控制性能提升。但故障发生后，飞行状态和控制输入的抖动变大，证明鲁棒性降低。因此选择合理的调节因子，可以既保证系统鲁棒性，也可以提升控制性能。

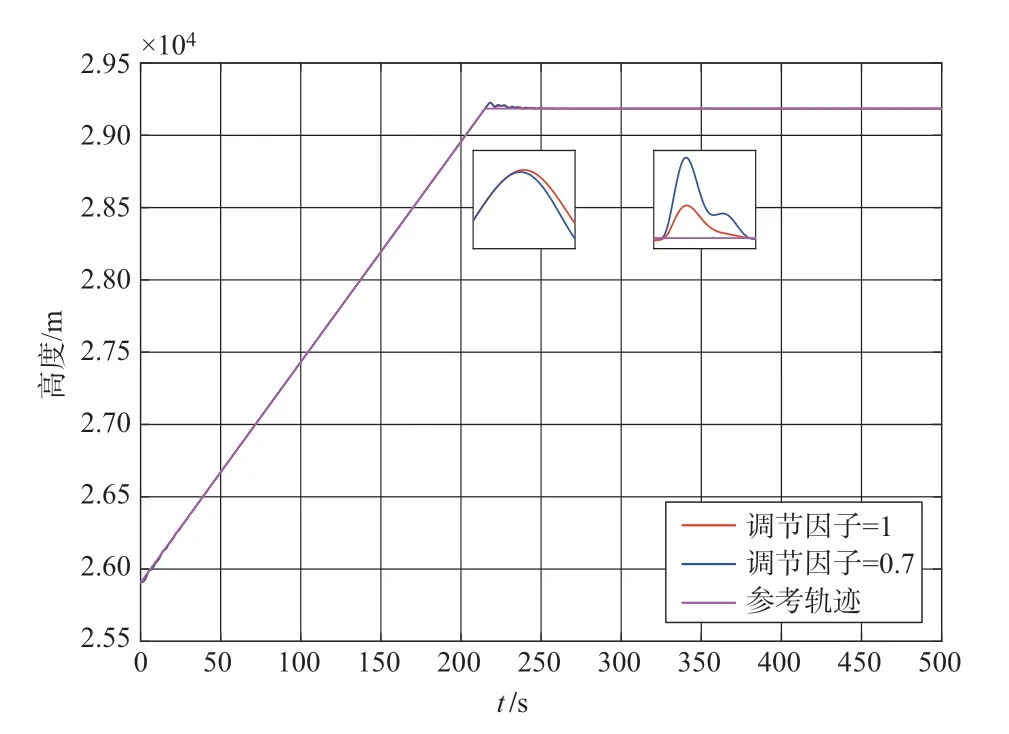
图3 加入调节因子的高度Fig.3 Altitude with adjustable factor

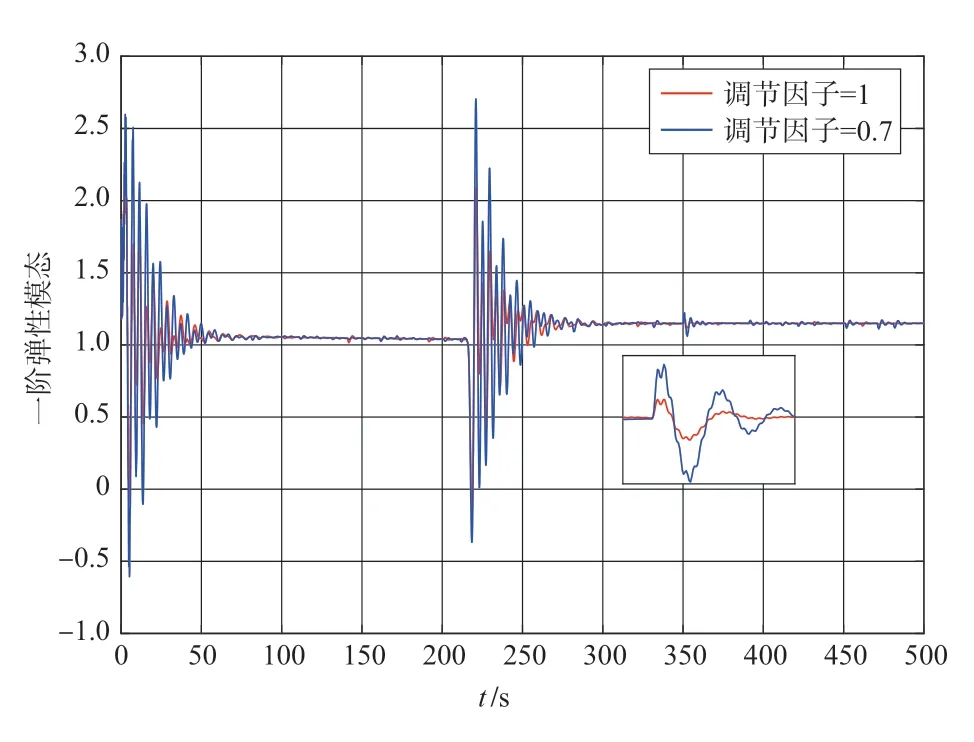
图4 加入调节因子的一阶弹性模态Fig.4 First order elastic mode with adjustable factor

图5 加入调节因子的舵偏角Fig.5 Elevator deflection with adjustable factor

5 结论

本文针对状态依赖输入饱和、参数不确定和执行器故障下的弹性高超声速飞行器，设计了基于可调Tube-MPC的容错控制器。在多胞线性参变模型基础上，针对反馈线性化后形成的状态依赖输入饱和问题，将虚拟输入约束上下限拟合为线性多项式，并通过SOS技术将多项式约束转化为线性矩阵不等式约束。考虑到故障发生的程度不同，为改善控制系统的保守性，引入了调节因子，改变不变集大小，以提升系统的控制性能。同时，将传统标称控制律设计为无约束与约束下的加权凸组合形式，使得虚拟输入满足约束。