基于ED-LSTM 的智能汽车神经网络横向动力学建模与控制1)
2022-08-26方培俊蔡英凤孙晓强
方培俊 蔡英凤 , 陈 龙 , 孙晓强 王 海
* (江苏大学汽车工程研究院,江苏镇江 212013)
† (江苏大学汽车与交通工程学院,江苏镇江 212013)
引言
随着驾驶员对车辆的安全性、机动性和乘坐舒适性要求的不断提高和控制理论的日益成熟,汽车智能化技术研究受到学者的广泛关注.由于智能汽车可以实现更好的道路利用率和更高的安全性,逐渐成为近年的研究热点之一[1-3].
轨迹跟踪控制是智能汽车行驶过程中一种应用广泛的重要技术,利用控制算法计算调节前轮转角,并在底层执行装置的作用下,使得车辆在沿着期望路径行驶过程中的横向位置偏差和航向偏差尽可能小,同时保证车辆具有一定的稳定性和行驶安全性[4].控制算法设计大多依赖被控对象的系统模型,因而,建立智能汽车动力学模型往往是控制系统设计的第一步.Jazar[5]将整车看作是一个刚体,建立了经典的2 自由度车辆动力学模型.Segel[6]将车辆当作一个线性的动力学系统,建立了包含横摆运动、侧向运动和侧倾运动的3 自由度车辆模型来描述转向响应.文献[7]采用魔术公式轮胎模型建立了非线性7 自由度车辆模型,研究了后轮转向系统对车辆操纵稳定性的影响.文献[8]建立了17 自由度模型,该模型对轮胎、悬架的非线性特性进行了充分描述.在控制算法中,许多方法都是通过基于理论推导的车辆动态数学模型计算出如车辆横摆角速度等描述车辆运动的物理量,然后设计反馈控制系统以进行跟踪.Liu 等[9]分析指出常规工况下使用线性2 自由度车辆模型的控制效果与14 自由度模型相当,但是极限工况下轮胎非线性与载荷转移在建模时不可忽略.Aouaouda 等[10]提出一种非线性模型预测控制方法,主要采用2 自由度线性车辆模型和魔术公式经验轮胎模型,设计了自动调节的模糊控制器,并结合带约束的迭代遗传算法,不断迭代调整模糊控制器的隶属函数和规则库以对车辆的转向进行控制,进而满足控制要求.王家恩等[11]基于7 自由度非线性车辆动力学模型设计滑模控制器,通过跟踪期望横摆角速度来保证车辆稳定地跟踪目标路径.文献[12-13]基于3 自由度非线性车辆动力学模型设计线性时变模型预测控制算法,以解决实时性差的问题,具有较好的控制效果.
实际上,智能汽车是一种复杂动力学系统,但基于理论推导的车辆动态数学模型通常在建模时进行了一定的理想化假设来简化车辆模型,这就导致无法通过实验数据来准确计算出车辆在行驶过程中的真实动力学响应,如车辆负载转移耦合效应、轮胎力耦合效应等.特别是在极限工况下,车辆系统和相关子系统会表现出高度非线性和强耦合特征.扩张模型维度虽然可以提高模型精度,但同时会增加建模难度,也给算法的快速求解带来了挑战,所以对其建模时需要权衡考虑模型的复杂度和保真度.此外,基于模型的轨迹跟踪控制方法通常受模型参数摄动、不确定性干扰、时滞以及执行机构饱和约束等影响[14-15],如果处于非线性区域中的轮胎被视为线性模型或驾驶环境突然变化,车辆的行为可能变得无法控制,导致智能汽车将失去路径跟踪能力和稳定性,进而导致车辆运行过程中路径跟踪精度低,稳定性差的问题.
近年来,随着深度学习和数据驱动技术的发展,多个研究领域产生了巨大进步,这一技术在智能汽车中同样得到了广泛应用.例如可以用来执行目标检测[16-18]、图像分割[19-20]、轨迹预测[21-22]等感知任务.有团队提出利用深度学习设计“端到端”控制算法,端到端[23-24]的方法由输入端的图像信息直接得到输出端的执行器指令,虽然可以实现从原始传感器数据直接得到车辆所需的控制量,但可解释性很低.Kabzan 等[25]采用相对简单的名义模型并通过高斯过程回归进行模型误差的在线学习,利用数据建立了机理混合模型,试验结果表明模型学习方法可以有效改善模型不确定性.神经网络具有很强的非线性建模能力,能够模拟不同类别的非线性代数方程和微分传递函数的解,许多学者研究用于动力学建模方面.文献[26]等研究并总结了建模所需的网络规模,结构和初始权重,并考虑了融合权重网络的影响,提出了一种在线培训方法和一种误差度量,这些误差度量代表了网络在一系列运行条件下的并行建模能力.Ji 等[27]提出组合基于Lyapunov稳定性理论和径向基函数神经网络的自适应控制机制.利用ANN 来近似估计轮胎转弯刚度的不确定性,结合车辆运动学、动力学模型确保轨迹跟踪控制时的鲁棒性和偏航稳定性.为提高赛车的圈速成绩,文献[28]利用赛车驾驶过程中车辆生成的大量数据,设计从数据中学习以提高性能的无人驾驶车辆模型和控制策略.但在车辆动力学应用中,大多数神经网络车辆动力学模型在学习完成后用于车辆状态估计和运动策略生成,且只关注神经网络对动态系统建模的能力和模型精度的提高.文献[29]指出,就他们所查阅的文献中还没有将深度神经网络用于轮式车辆的耦合控制,因此如何将学习的神经网络模型与无人驾驶控制算法相结合的研究较少.
本文基于数据驱动方法建立了一种用于轨迹跟踪控制的新型神经网络车辆动力学多步预测模型.分析车辆单轨模型并考虑轮胎非线性和纵向负载转移,基于编码器-解码器结构,采用串行排列来扩展微分方程进而设计模型,并对模型精度进行比较评估.根据车辆稳态转向假设,动力学前馈控制利用提出的模型计算所需的前轮转向角和稳态侧滑角.将稳态侧滑角纳入基于路径误差的转向反馈中,实现参考轨迹跟踪控制.最后,通过仿真验证了所提模型及算法的准确性及可靠性.
1 车辆横向动力学建模
车辆在地面运动的动力学变化过程十分复杂,建立合理的车辆动力学模型是实现智能汽车轨迹跟踪功能的基础.
1.1 单轨模型
汽车(前轮驱动、转向)具有纵向、横向、垂直方向的平动以及侧倾、俯仰、横摆3 个方向的转动.其中,横向运动和横摆运动基本上是由转向操纵产生的.为了较为准确地反映车辆运动特性的同时考虑减少基于模型的控制算法的计算量,通常进行适当的理想化假设以简化车辆模型.当横向及速度和横摆角加速度较小时,常采用简化的车辆单轨模型(single track model,STM),如图1 所示,U为车辆质心处的速度;Ux,Uy分别为质心处沿车体坐标系x,y方向的速度;αf,αr分别为前后轮侧偏角;β为质心侧偏角;r为横摆角速度;a,b是质心距前后轴的距离;Fyf,Fyr分别为前、后轴轮胎受到的横向合力;Fxf为前轴轮胎受到的纵向合力;δ为前轮转角.该横向动力学模型可用微分方程表示为

图1 物理车辆单轨模型Fig.1 Physical vehicle single-track-model
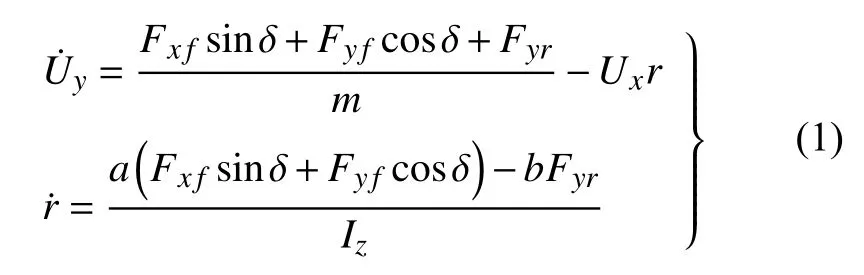
实际上,车辆在不同路况下的行驶过程中产生的非线性特征是由于轮胎在转弯时引起的,所以为了拓展车辆模型的适用范围,引入轮胎的非线性模型,即

其中,Cα和μ是轮胎侧偏刚度与路面附着系数;Fz是轮胎垂向载荷;αsat是轮胎饱和侧偏角.前后轮胎侧偏角计算公式为
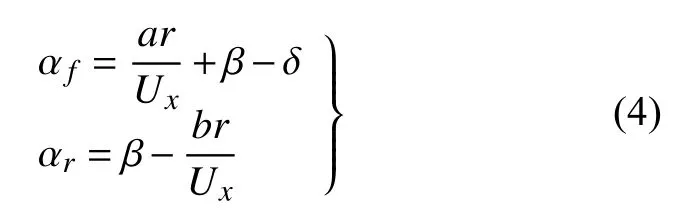
当车辆处于高性能行驶时,由于车辆加速或制动而增加或减少在每个轮胎上承受的垂向力,进而产生的纵向重量传递也影响着车辆的横向动力学.其中hCG是到车辆重心的高度,g是由于重力引起的加速度,L是车辆轴距.与非线性轮胎模型结合使用时,重量传递会增加或减小轮胎所受垂向力的大小,进而影响轮胎横向力的大小,前后轴垂向力Fzf,Fzr的计算公式为

1.2 编码器-解码器结构
深度学习理论中的编解码结构(encoderdecoder,ED)的具体运行机理为:首先使用编码器把原始数据处理成一种上下文张量,然后将其输入到解码器中,最终输出所需要的结果形式.长短时记忆网络(long short term memnory,LSTM)是循环神经网络的一种变体,相比前馈网络,计算效率较高,能够提取数据的时序特征,可以处理时序预测建模问题.相比一般的神经网络来说,不仅拥有非线性建模能力,还解决了训练过程中存在的梯度消失和梯度爆炸的问题.假设训练样本充足且良好,LSTM 可以利用记忆单元和遗忘门揭示时间预测问题中的长期依赖关系.由于其良好的性能,LSTM 在驾驶员辅助系统的时间序列预测中得到了广泛应用.行人轨迹预测、公路轨迹预测等示例应用已经显示出能够模拟交通参与者的横向和纵向动力学.
时下解决预测任务最为流行的框架是基于LSTM 的编码器-解码器框架,车辆的动力学状态变化由于具有很强的时序相关性,因此这种基于LSTM 的编-解码器结构可以用来解决车辆动力学变化预测任务.图2 中的示例显示了该结构的具体计算细节,编码器是一个时间维度为4 的LSTM,每个时步的隐藏状态用(h1,h2,h3,h4)表示.(x1,x2,x3,x4)为4 个观测时步LSTM 编码器的输入,编码器通过内部计算得到中间语义向量c;而解码器是一个时间维度为4 的LSTM,该解码器获取中间语义向量,并在每个时步的隐藏状态 (h'1,h'2,h'3)中传递,最终获得(y1,y2,y3)3 个预测时步的输出.
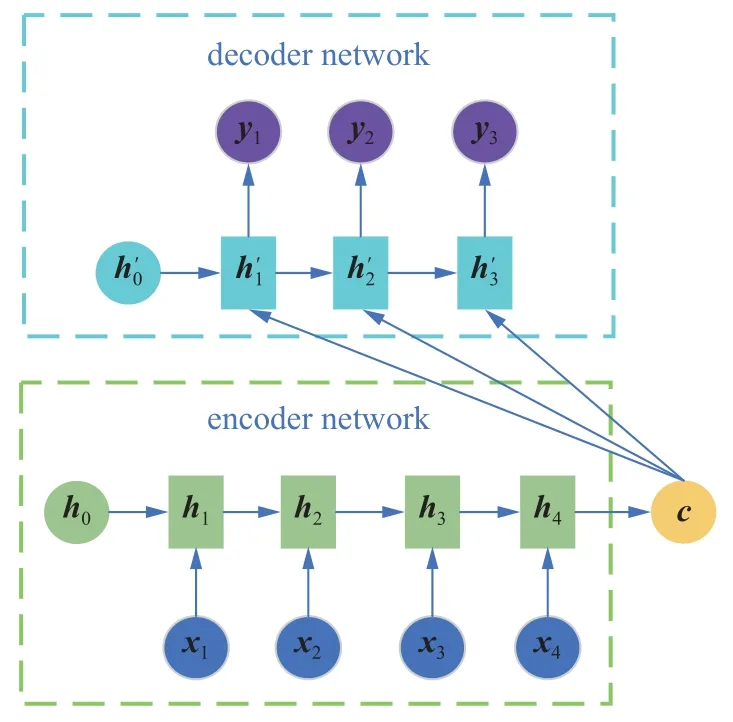
图2 基于LSTM 的编-解码器框架结构Fig.2 Encoder-decoder framework based on LSTM
1.3 ED-LSTM 车辆横向动力学多步预测模型
基于上述分析设计ED-LSTM 车辆横向动力学多步预测模型,具体的模型结构如图3 所示.EDLSTM 车辆横向动力学多步预测模型输入端为4 个时步的车辆控制与状态数据,输出端是计算当前时刻和预测未来4 个时刻的车辆横摆角速度和横向速度的微分.单轨模型具有确定性和可解释性,神经网络用来检测单轨模型的不足,优化补全单轨模型初始输出所丢失的信息,通过合并这两个协作的模型,以实现改进的全局性能.其具体原理为:输入特征向量输入到前文建立的车辆单轨模型中,在考虑轮胎非线性及负载转移效应的前提下,计算提供基于单轨模型的数据前处理提供4 个时步的的物理基准信息.与输入特征向量进行级联合得到新的4 个时间步长的车辆状态与控制数据组合,并采用文献[30]提出的串行排列,车辆运行历史时步的状态及控制数据(r,Uy,Ux,δ,Fxf)和物理基准信息()输入到LSTM 神经网络中,通过第一层编码器对数据时序特征进行编码,获得车辆历史横向动力学的高级语义表达c,第二层解码器实现特征解码,计算并预测得出车辆在当前时刻和未来时刻的横向动态变化量.具体地,ED-LSTM 车辆横向动力学多步预测模型的前向计算过程如式(6)所示
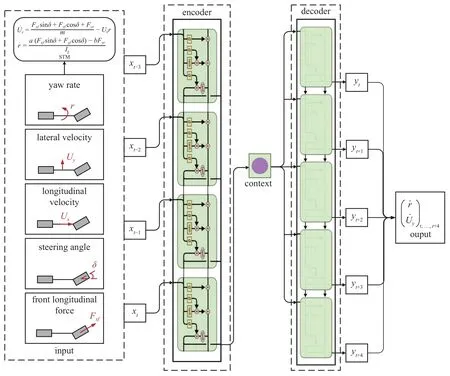
图3 ED-LSTM:车辆横向动力学多步预测模型Fig.3 ED-LSTM:Multi step prediction vehicle lateral dynamics model
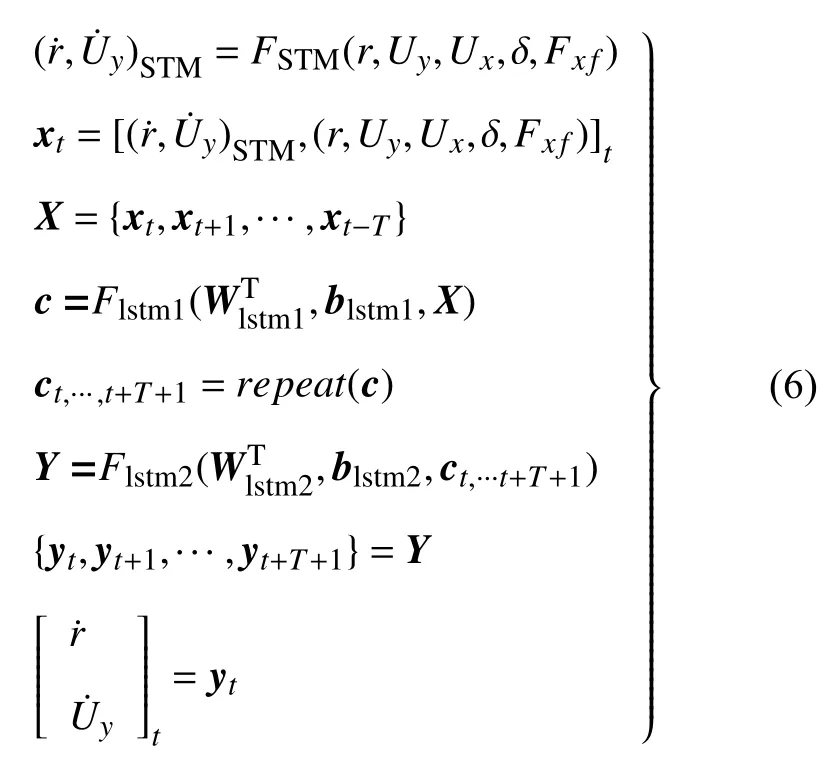
式中,xt表示各时步状态和控制输入数据,X表示状态和控制输入的历史信息组合,yt表示模型计算输出的车辆横摆角速度和横向速度的微分,Y表示模型预测输出的未来信息组合,Wlstm{1,2},blstm{1,2}表示LSTM 网络的权重参数.
与拟合基于物理分析的单轨模型中的参数不同,通过在数据中包含车辆未知或未建模的车辆动力学信息,使得该模型可以学习到车辆的全局动力学状态变化,例如轮胎非线性效应、负载转移等潜在或物理模型未考虑建模的部分.模型训练完成后,提取网络权重参数组合,将式(6)简化如式(7)所示

式中,θ表示训练得到模型权重参数组合,fED-LSTM是所提出模型的缩写.
2 数据获取及模型训练
本文主要研究一种能在不同驾驶条件下准确计算并预测车辆横向动力学响应的神经网络动力学模型.为充分描述车辆的横向动力学特性,将从仿真环境和实际环境中通过输入车辆操作信号来产生车辆响应,进而收集所需的输入和输出数据来对表示车辆横向动力学的神经网络进行训练,并对比不同模型的计算结果.
2.1 数据集制作
2.1.1 仿真数据获取
从仿真环境中收集了许多驾驶场景的数据.在这个过程中,Crasim 软件提供高保真动力学模型及用于渲染道路环境,采用Logitech G29 转向踏板系统输入控制车辆的操作信号,Simulink 与Carsim 联接,前者接受来自底层的控制信号,后者通过其动态模型执行并反馈相关动力学操作,获取其中的通信来收集数据.仿真数据采集系统结构如图4 所示.
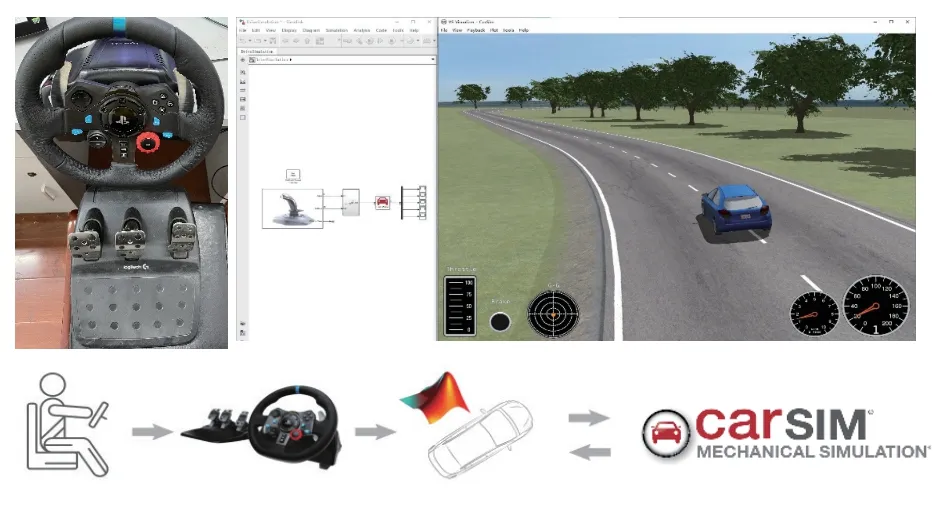
图4 仿真数据采集系统结构Fig.4 Structure of simulation data acquisition system
由于路径轮廓对车辆的操控性能有显著的影响,为了收集数据,车辆在多种不同的道路类型上多次行驶,主要包括直路(高速公路)、弯路(赛道)、城市街区(不同转弯的混合).在不同的路况下,也经常进行不同的操作,如单车道、双车道变换,避障,掉头等.为了测试神经网络横向动力学模型对不同参数变化的能力,采集了良好干燥路面μ=0.85 和湿路面μ=0.5 不同条件下的数据.此外,还考虑了不同负载条件下的数据.为了模拟这种情况,车辆的质量会因车辆上有乘客而变化.在没有乘客的情况下,考虑车辆的整备质量.对于单乘客情况,车辆的质量增加70 kg.为简单起见,假设附加质量均匀地分布在车辆上.
2.1.2 实车数据获取
为了证明利用实际车辆收集到的动力学数据进行神经网络车辆动力学模型的建模可行性,并验证在实际道路中不同路面条件下该模型的计算和预测效果,利用智能驾驶平台“奇瑞艾瑞泽”采集了大约行驶时间为1 小时的有效轨迹样本.采集到的数据涵盖了实际情况下智能汽车在不同驾驶风格、不同温度时行驶在干燥、潮湿沥青路面条件下的动力学响应数据,并保证试验数据在高、低附着系数下大致平均分配.该试验平台如图5 所示,包括了环境感知系统、惯性导航定位系统、决策控制模块和底层线控执行机构,并安装有车轮力传感器、S-Motion DTI 和MSW DTI 传感器,并接受来自CAN 总线的数据.

图5 实车数据采集车Fig.5 Real vehicle data acquisition system
2.2 模型训练
为了对比神经网络横向动力学模型和简化的单轨模型的建模能力,使用上述数据用来训练网络和识别确定单轨模型的最佳拟合物理参数.将收集到的数据集分为三个部分.划分总数据的70%用于训练,15%用于验证,其余15%用于测试.并对数据进行随机化抽取处理以打破数据集的时间相关性,保证每个数据样本均由与时间相关的状态轨迹组成,但任何给定的两个数据样本间无相关性.
在配备英特尔i9 处理器和64 GB 内存的计算机器上,使用基于Pytorch 的学习框架,并使用Nvidia 1080 Ti 图形处理单元并行化加速训练.基于梯度的优化技术“Adam”用于训练多层网络.对于每个N=64 单位的隐藏层,使用Relu 激活函数.使用1000 个小批量,学习速率为0.001.训练NN 进行10 000次迭代.训练损失函数定义为
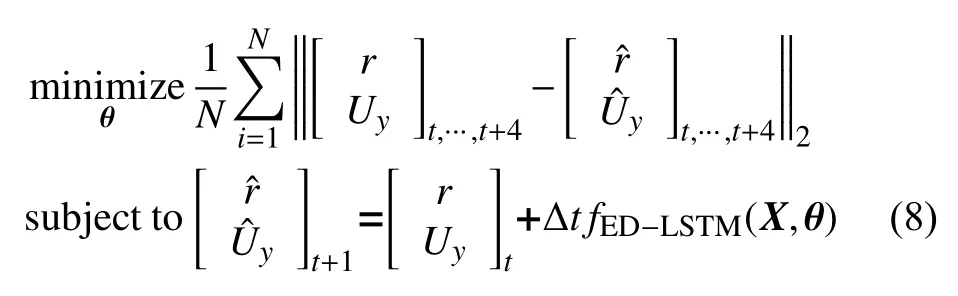
2.3 训练结果
2.3.1 仿真数据模型训练结果
混合不同道路摩擦系数下的仿真数据来训练所提出的神经网络车辆横向动力学模型的过程如图6(a)所示.使用训练完成的模型对未知数据(测试集)进行泛化能力的测试.图6(b)显示了该模型应用测试集数据计算并预测不同时步的横摆角速度及侧向速度微分的均方误差(MSE).
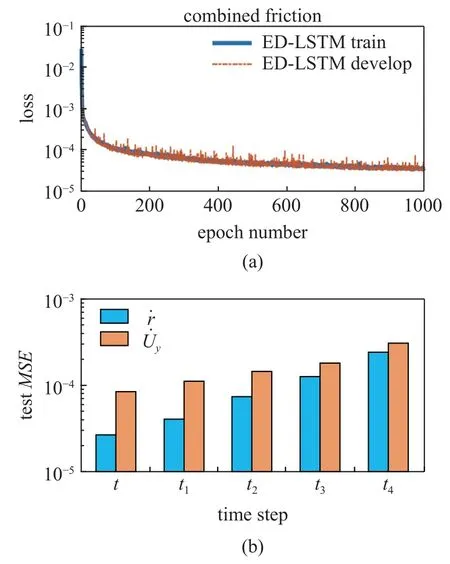
图6 模型训练、验证及测试结果Fig.6 Model training,validation and test results
设置不同的摩擦系数,采集车辆分别在不同速度下跟踪双移线轨迹的动力学状态数据,并对比评价所提出的神经网络模型与不同自由度的物理车辆模型输出精度.车辆物理模型进行大量简化且仅由牛顿力学分析表示,通过车辆当前状态及控制数据来计算状态变化量,故不适用于多步预测.神经网络模型使用编码器-解码器结构,可以实现对车辆状态及变化量未来多个时步的准确预测,其预测值及预测趋势如图7(b)和图7(c)中的局部放大图所示.
在图7 中,不同摩擦系数的测试结果使用虚线垂直线进行划分.第一部分为μ=0.85 时的路面摩擦系数计算结果,第二部分为μ=0.5 时的路面摩擦系数计算结果.对比神经网络模型和物理模型的第一时步计算精度,神经网络模型的精度明显优于物理模型,原因在于使用高保真度的车辆模型生成数据集时,神经网络车辆横向动力学模型可以通过其隐藏节点单元来学习车辆在较低速度下进行转弯操作时由于轮胎产生弹性迟滞现象而产生的侧偏角高阶动态效应和由于急加、减速或急转弯时的纵横向重量转移效应等非线性现象.
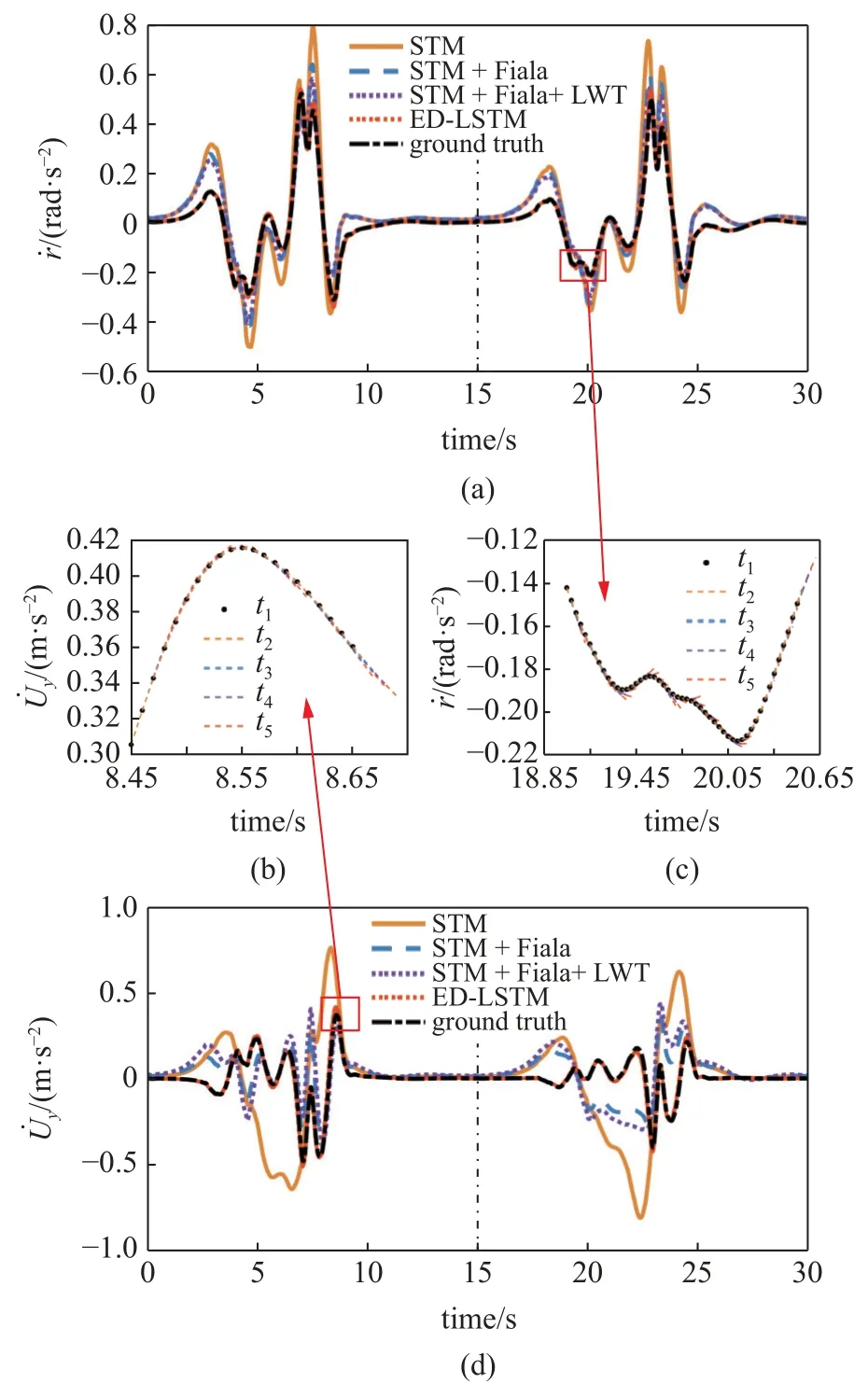
图7 模型精度对比Fig.7 Model accuracy comparison
图7(a)和图7(d)显示了四个模型的横摆角速度微分计算值、横向速度微分计算值和真值的对比.当摩擦系数变化时,识别出的物理车辆模型仅能通过当前的输入和状态来计算车辆的动态变化,其拟合得到的车辆参数近似表示了路面的平均状态,而神经网络模型通过包括状态和输入的多个延迟时步信息可以隐式地学习和应用于不同的道路条件下的车辆动力学响应.车速和摩擦系数会对横向速度微分值计算产生较大的联合影响,但神经网络模型可以较好地包含这些因素的影响,从而准确计算车辆在不同运行速度及路面条件下的动力学状态变化.
2.3.2 实车数据模型优化结果
选取混合摩擦系数仿真数据预训练完成的模型,结合实车数据进一步优化神经网络车辆横向动力学模型权重参数,使得模型输出更适合实际车辆的动力学变化响应.实车数据也用来识别物理车辆模型的相关参数,其中包括非线性轮胎和纵向负载转移的影响.实际车辆测量得到的数据相对嘈杂,采用截止频率为3 Hz 的二阶Butterworth 低通滤波器进行数据平滑,滤除悬架振动等高频行为对车辆动力学的影响.
图8 以相关图的形式显示了两个模型在不同路面条件下使用车辆状态数据的计算结果比较.在图8中,点离直线越近,模型拟合越好.物理车辆模型的测试误差较大.原因是其仅围绕单个操作点进行显示计算,无法捕捉不同摩擦条件对物理参数的影响.神经网络模型的计算精度显著提高,该模型对不同路面的数据具有良好的适应和预测性能.因此,所提出的模型具有良好的实车数据建模可行性,可以对车辆行驶的路面上提供适当的预测,而无需进行明确的道路附着系数估计.

图8 实车数据验证相关图Fig.8 Correlation diagram of real vehicle data test
3 算法设计及控制结果分析
3.1 基于ED-LSTM 的智能汽车轨迹跟踪控制器设计
基于车辆稳态转弯运行条件的假设下,给定参考路径的曲率和车辆的纵向速度,利用单轨模型可得到前馈轮胎横向力,结合轮胎模型可将这些稳态轮胎力转换为所需的前馈转向角,通过横向偏差e和航向偏差 Δψ 计算反馈转向角,相加得到最终的转向命令.以基于单轨模型控制算法所提供的控制精度为基准进行比较,利用训练完成的ED-LSTM 车辆横向动力学多步预测模型进行轨迹跟踪控制算法使用相同的稳态假设,训练及控制流程如图9 所示.

图9 基于神经网络车辆动力学模型横向控制流程图Fig.9 Lateral control flow chart of vehicle dynamics neural network model
为了得到前馈转向角和质心侧偏角,利用二阶非线性优化方法求解神经网络横向车辆动力学模型的平衡点.测量的车辆纵向速度和参考路径曲率作为优化求解器的输入,以计算正确的前馈转向命令.
基于车辆稳态转弯假设

结合运动学原理,得到
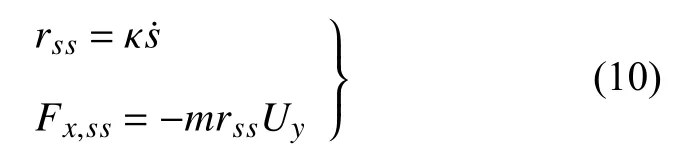
如前所述,车辆运行过程中的历史3 时步及当前时刻的状态及控制数据信息输入模型后即可得到当前时刻及未来4 时步的横摆角速度和横向速度的微分变化量,即

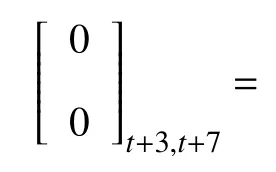

为计算合适的控制输入,具体使用带约束的二阶内点法来求解式(14)所示的非线性优化问题,将基于运动学原理的稳态转向角作为 δffw的初始值进行优化迭代,最终计算得到在转向极限约束 (δu,δl)范围内的稳态平衡时的 δffw,Uy,ffw.

利用稳态前馈横向速度和纵向速度计算得到稳态前馈质心侧偏角,即

为了补偿前馈转向产生的误差和扰动,同时使用基于路径的转向反馈控制器来补偿跟踪期望的轨迹.将车辆稳态质心侧偏角纳入反馈控制可以提高路径跟踪的效果,且保持预瞄转向反馈的鲁棒稳定性.该反馈控制转向角最终基于稳态前馈质心侧偏角,车辆偏离期望轨迹的横向偏差e和车辆偏离期望轨迹的航向偏差 Δψ,即

因此,将得到的前馈转向角和反馈转向角相加得到最终的横向路径跟踪转向角,即

3.2 联合仿真分析
为验证基于ED-LSTM 的轨迹跟踪控制算法的有效性,提取训练完成的模型权重,调整仿真车辆参数,搭建Simulink/CarSim 联合仿真模型.
双次换道轨迹[31]是车辆在完成第一次由本车道换道至临近车道后,再次换道回至本车道的曲线.在实际车辆行驶中该轨迹较为常见,是国内外研究学者用于验证智能汽车中高速工况下轨迹跟踪控制性能的典型工况之一.双次换道轨迹由两条换道曲线组成,以第一次换道曲线为例,换道曲线方程为

式中,d为换道的横向距离,即为常规车道宽度,取d=4 m;l为换道任务完成后车辆在纵向方向上运动的距离,考虑一种较为紧急的换道状况,取l=40 m.
仿真工况设置为路面附着系数为μ=0.85,车速为Ux=20 m/s 的双次换道轨迹跟踪控制.基于EDLSTM 和STM 的轨迹跟踪控制效果如图10 所示.两种控制方法实现基于模型的动力学前馈控制和基于路径误差的反馈控制,可以有效跟踪参考轨迹,完成车辆在中高速下紧急换道任务.由图11(a)和图11(b)可知,两种控制算法在路径曲率较大处的横向位置偏差和航向误差较大.
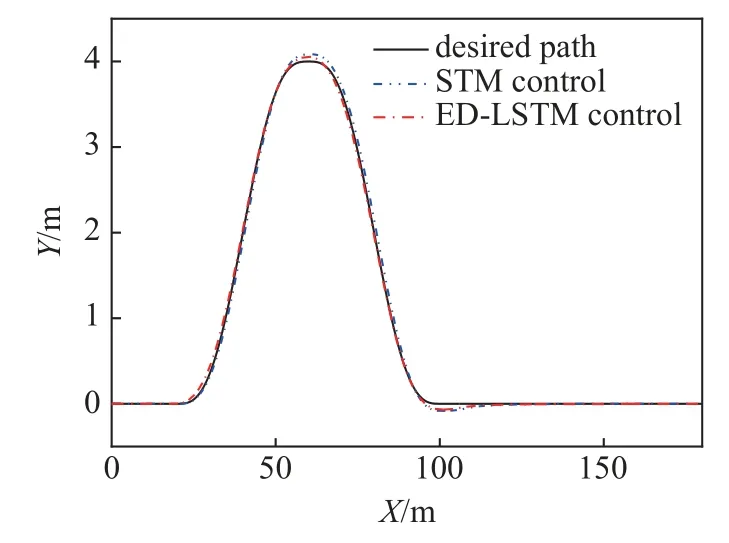
图10 双次换道曲线轨迹跟踪仿真对比Fig.10 Trajectory tracking simulation comparison in double-lane change
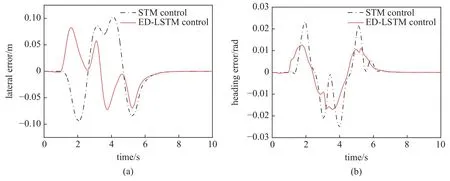
图11 横向跟踪误差、航向误差对比Fig.11 Lateral errors,heading error comparison
如表1 所示,基于ED-LSTM 的轨迹跟踪控制的横向误差为-0.082 5~0.072 6 m,航向误差为-0.017 0~0.012 6 rad.相比于基于STM 的轨迹跟踪控制峰值横向误差降低19.49%,峰值航向误差降低32.45%.
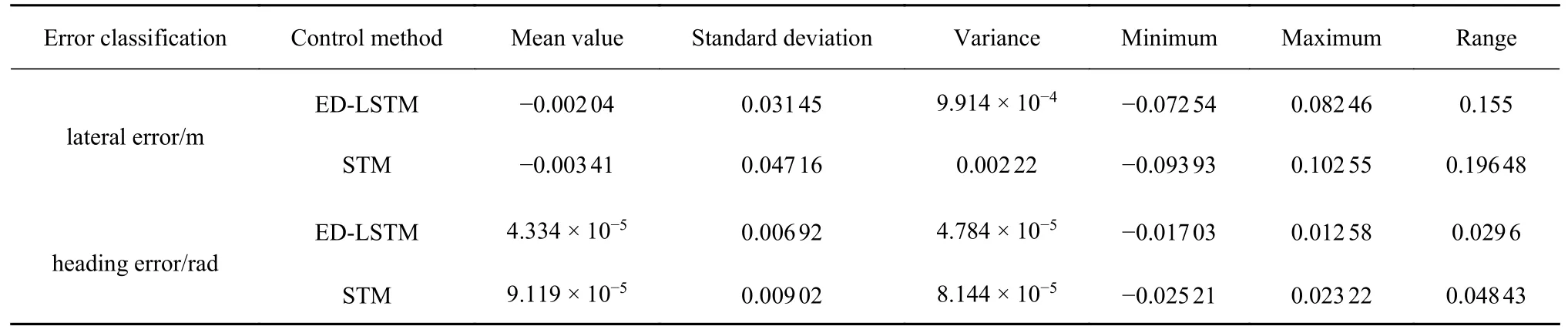
表1 跟踪误差评价指标Table 1 Evaluation indexes of tracking error
图12 所示为两种算法在轨迹跟踪过程中的车辆控制量,在相同的稳态假设和控制体系结构下,由于ED-LSTM 比STM 具有更好的模型保真度,且将对未来路径及状态的预测应用于动力学前馈控制中,从而降低了转弯中段的跟踪误差.此外,反馈控制算法主要受控制增益、前视距离等转向反馈参数的影响,车辆在整体运行过程中特别是当运行至双次换道工况结束出口时,由于其横向位置偏差和航向误差较小,更加接近所期望的路径,所以前轮转角输入值稳定平顺,在一定程度避免了控制量超调抖动的问题,进而减少了车辆双次换道工况结束时的横摆振荡,确保了轨迹跟踪控制的局部稳定性.图13(a)~图13(c)所示为应用两种控制方法的车辆动力学状态,包括车辆横向加速度、质心侧偏角及横摆角速度.结果表明,基于ED-LSTM 的峰值横向加速度为5.38 m/s2,基于STM 的峰值横向加速度为5.93 m/s2,基于ED-LSTM 控制的质心侧偏角和横摆角速度峰值均明显小于基于STM 的控制方法,证明车辆运行在强非线性区域时依然获得了更好的动态性能,且无质心侧偏角及横摆角速度抖动现象,实现了轨迹跟踪控制精度和稳定性的同时提升,获得了更优的轨迹跟踪性能.

图12 前轮转角输入对比Fig.12 Steer angle input comparison

图13 横向加速度、质心侧偏角、横摆角速度对比Fig.13 Lateral acceleration,sideslip angle,yaw rate comparison

图13 横向加速度、质心侧偏角、横摆角速度对比(续)Fig.13 Lateral acceleration,sideslip angle,yaw rate comparison(continued)
3.3 HiL 实验测试
为进一步验证本研究提出的控制方法的有效性,搭建硬件在环(hardware in the loop,HiL)仿真测试平台,如图14 所示.该平台主要包括上位机系统、实时仿真机系统以及整车控制器.

图14 HiL 测试平台架构Fig.14 HiL test platform architecture
HiL 测试工况设置为路面附着系数μ=0.85 的变速“8”字形轨迹跟踪控制,8 字形路径由两条直线和两条曲率为0.01 的平滑曲线组成,其中曲线部分车速为80 km/h.
如图15 所示,在真实的控制器当中,所提出的基于ED-LSTM 的控制方法可以在较高的车速下较好地完成轨迹跟踪任务,具有良好的控制精度.分析图16 可以看出,车辆的横摆角速度与质心侧偏角很好地控制在稳定范围内,但由于控制算法是在真实控制器中计算运行,且控制器存在运算速度限制、CAN 信号传输延迟,实时仿真机内数据采集与处理的迟滞等因素影响,所以存在一定的时滞效应,且在转弯处由于曲率突变会导致相对较大状态量幅值变化,但仍在可接受的控制范围内.
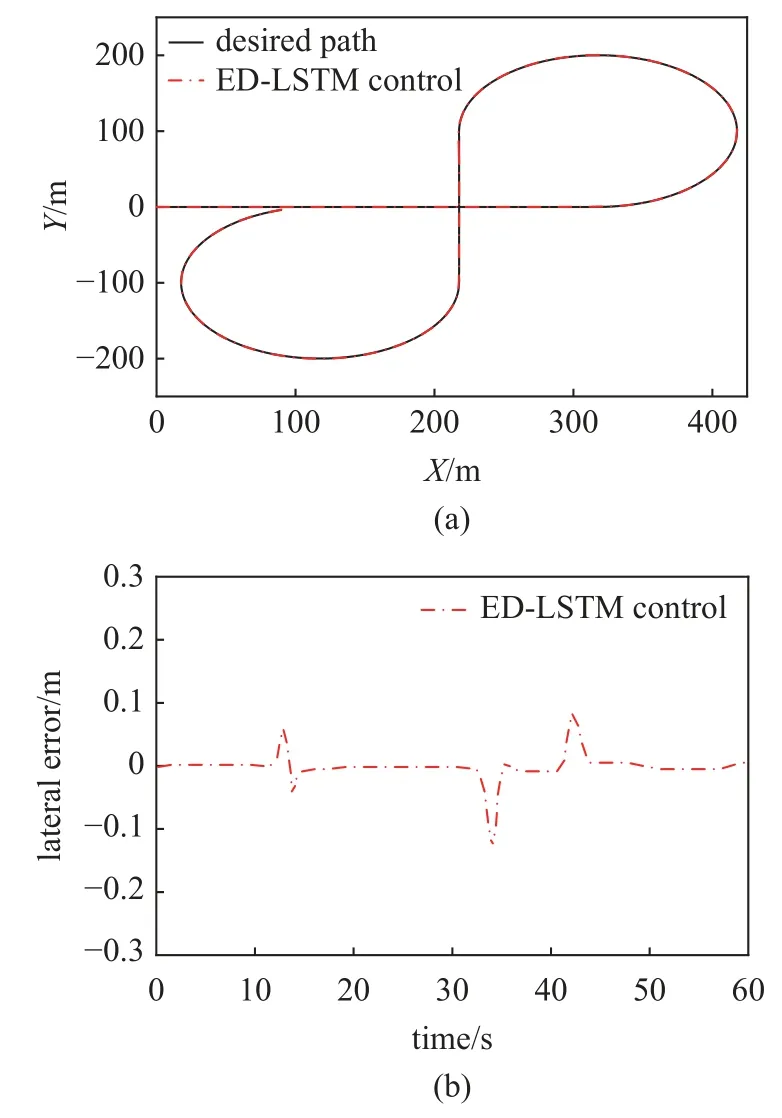
图15 “8”字形曲线轨迹跟踪控制效果Fig.15 “8” shape curve trajectory tracking control effect

图16 车辆动力学状态Fig.16 Vehicle dynamics status
4 结论
本文基于数据驱动方法研究车辆横向动力学建模与控制问题.引入轮胎非线性模型且考虑纵向负载转移效应来建立物理车辆单轨模型,基于编码器-解码器框架设计神经网络横向动力学多步预测模型,该模型采用LSTM 用来提取数据的时序特征以解决时序数据建模预测问题.使用串行排列来扩展微分方程描述不完全的动力学信息,兼顾物理模型的可解释性和神经网络的非线性,进而提高该模型的全局计算精度.通过在制作的数据集中包含不同摩擦系数路面条件下车辆的动力学状态信息,提出的模型可以利用其隐藏节点、状态和控制的多个时间步长输入时序特征来学习车辆的非线性和耦合性,并可对路面条件做出适当的预测,而不需要进行明确的路面附着系数估计.此外,轨迹跟踪控制由基于ED-LSTM 的前馈算法和基于路径反馈算法组成.根据车辆稳态转弯假设,利用训练完成的模型计算前馈前轮转角和稳态质心侧偏角,将稳态质心侧偏角纳入基于路径的反馈控制,在提高路径跟踪的效果同时,保证转向反馈的鲁棒稳定性.实验证明了仿真及实车数据驱动建模可行性和控制有效性,同时对比基于单轨模型的轨迹跟踪控制算法,所提出的控制策略可以实现更高的轨迹跟踪精度和更好的横向行驶稳定性.
