基于FFUKF 路面附着系数估计的汽车牵引力控制1)

汪洪波 王春阳 高 含 徐世寒

(合肥工业大学汽车与交通工程学院,合肥 230009)

引言

汽车牵引力控制系统 (traction control system,TCS)是汽车主动安全控制关键技术之一,TCS 系统通过发动机输出转矩控制和主动制动控制调节驱动轮滑转率在最优范围内,在实现驱动稳定性前提下提高汽车的加速性能[1].汽车—驾驶员—道路组成的系统具有瞬变的特点,若想达到较好的控制效果,对其关键状态参量的估算尤其是对路面状态的估计至关重要[2].

国内外诸多学者对路面附着系数的估计做了广泛的研究工作[3-5].王博等[6]指出目前路面附着系数估计主要分为Cause-based 和Effect-based 两类.Causebased 主要使用传感器(光学、声学、微波等)测量影响路面附着系数的主要因素,通过经验模型估计附着系数[7-8],但此方法受工作环境等影响较大,并且成本较高,难以商用.Effect-based 主要通过建立观测器分析附着系数,对车轮或车身运动响应进行估计,目前多数研究属于Effect-based 方法.基于Effectbased 的附着系数估计算法主要有基于 μ-s曲线斜率的估计方法[9-10]、卡尔曼滤波[11-13]等.与扩展卡尔曼滤波(extended Kalman filter,EKF)相比,无迹卡尔曼滤波(unscented Kalman filter,UKF)采用真实的非线性模型,用随机变量逼近状态分布,而不是将非线性函数线性化,可以处理不可导的非线性函数,保证了轮胎在非线性情况下的滤波精度[14],适用于轮胎-路面附着系数这种强非线性系统.Chen 等[15]基于改进的Dugoff 轮胎模型,利用无迹卡尔曼滤波和MSE 加权融合获得道路附着系数,但传统的UKF具有记忆性,如果过滤器的初始化不够接近实际状态,它可能会发散,同时旧数据的累积会减小新获得的数据对滤波的更新作用,因此导致UKF 无法快速跟踪系统参数的变化[16-18].

在TCS 控制器方面,对控制方法研究集中在 PID、逻辑门限、模糊逻辑、神经网络以及滑模控制等[19-20],而以路面附着系数估计为基础进行TCS 控制能够实现更好的控制效果.Ding 等[21]提出了一种基于模糊逻辑理论的轮胎-路面附着系数估计方法,在此基础上综合PID 控制器对车轮滑转率进行控制,实现了良好的控制效果.在多数研究中TCS 控制依赖路面附着系数估计,一旦路面附着系数估计不准确,控制效果会急剧下降.

高精度、快收敛的路面附着系数估计算法能够有效提升TCS 控制效果,本文将模糊控制和衰减记忆滤波思想引入UKF,设计基于模糊遗忘因子的无迹卡尔曼滤波估计算法,以提高滤波算法的跟踪性.在TCS 设计方面,本文根据车辆行驶状态和路面状态,应用可拓理论,将基于附着系数和基于车辆加速度计算的基础扭矩进行可拓融合得到目标基础扭矩,之后以实际滑转率和目标滑转率之间的误差作为输入,设计模糊自整定PI 控制器得到反馈扭矩,控制驱动轮滑转率接近其目标滑转率,以避免因附着系数估计不准确而导致TCS 控制变差的问题.

1 车辆和轮胎模型

1.1 五自由度整车动力学模型

本文研究的牵引力控制只考虑车辆水平直线行驶的情况,不涉及车辆横向运动和横摆运动,试验车型为4×2 后驱牵引车.因此,考虑模型精度和计算量,本文采用五自由度整车动力学模型来描述车辆运动状况,分别为车身的纵向运动和四个车轮的转动.五自由度整车动力学模型简图如图1 所示,OX正方向为车辆行驶方向,其中O为车辆质心位置,车轮顺时针旋转方向定为正方向,下标fl,fr,rl,rr分别表示车辆的左前轮、右前轮、左后轮和右后轮.

图1 五自由度车辆动力学模型简图Fig.1 Diagram of 5-DOF vehicle dynamics model

整车的纵向运动方程

式中,m为车辆质量,单位为kg,ax为纵向加速度,单位为 m/s2,Fw为空气阻力;Fx,ij为各轮处纵向轮胎力,单位为N.

对于空气阻力Fw,计算公式如下

式中,CD为空气阻力系数,A为车辆迎风面积,单位为 m2,vx为纵向车速,单位为km/h.

车轮旋转运动微分方程

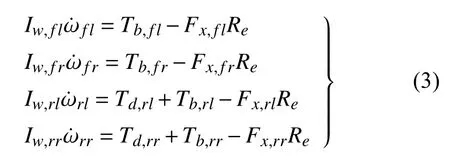
式中,Iw为车轮转动惯量,单位为 kg·m2,ω 为车轮转速,单位为 rad/s,Tb为作用于车轮的制动力矩,单位为 N·m,Td为作用于车轮的驱动力矩,Re为车轮有效转动半径,单位为m.

进一步地,当车轮未打滑或滑转率较小时,有

式中,Ft为驱动力,Fj为加速阻力,Ff为滚动阻力.

对于Ft,Fj,Ff,计算公式如下

式中,Te为发动机扭矩,ig为变速器当前传动比,i0为主减速器传动比,ηT为传动效率,δ 为车辆旋转质量换算系数,f为滚动阻力系数.

考虑加速、制动过程中的纵向载荷转移,各个车轮所受到的地面法向反作用力近似计算公式如下

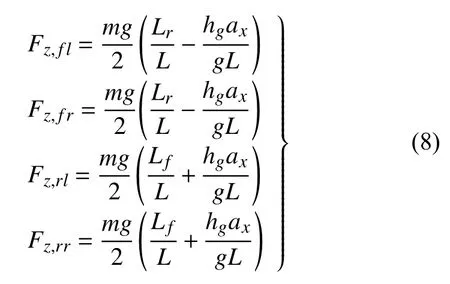
式中,L为轴距,Lf为车辆质心到前轴距离,Lr为车辆质心到后轴的距离,hg为质心高度.

1.2 轮胎模型

Dugoff 轮胎模型[22]是一种应用广泛的半经验轮胎公式,具有近似高精度的特点.为了准确地表达轮胎的非线性力学特性,该轮胎模型引入了边界值L对模型进行了修正,从而可以得到描述轮胎纵向力和侧向力与路面附着系数之间的函数表达式.Dugoff 轮胎模型的输入输出如图2 所示.

图2 Dugoff 轮胎模型输入和输出Fig.2 The input and output of Dugoff tire model

对于单个轮胎受力分析,在轮胎坐标系下经过受力分解得到纵向力与侧向力的表达式如下

其中

式中,Fz,kN=,μ为路面附着系数,ε 为速度影响系数,可通过仿真和实车试验标定得到,L为边界值,主要用于轮胎非线性区间轮胎力的拟合;Cx和Cy分别为轮胎的纵向刚度和侧偏刚度,其与轮胎结构、材料和轮胎垂直载荷有关.通过仿真与实车试验,本文得到轮胎参数Cx=76.8 kN/rad,Cy=103 kN/rad,ε=1.16.

由Dugoff 轮胎模型公式可知,路面附着系数与公式中其他参数没有关联,因此可将Dugoff 轮胎模型中的路面附着系数分离出来,式(9)和式(10)修改如下

2 路面附着系数估计

2.1 基于模糊遗忘因子的无迹卡尔曼滤波

传统路面附着系数算法常常选取需要估计的状态变量为四个车轮处路面附着系数,而对于本文所研究的后驱商用车TCS 来说,其控制对象为驱动轮,同时车辆处在均一和对开路面需要采取不同的控制策略,所以状态向量选取左右两侧驱动轮下的路面附着系数 μl和 μr,这样可以简化模型,减小计算量,同时也满足TCS 控制的设计要求.车辆的纵向加速度和左、右驱动轮轮速对路面附着系数比较敏感,因此,量测变量选取ax,ωrl和 ωrr.本文采用的基于离散非线性系统的无迹卡尔曼滤波,其实现步骤较长,由于篇幅限制,在此不再赘述.

对于时不变系统,传统无迹卡尔曼滤波能够实现较高的估计精度[23],但随着无迹卡尔曼滤波过程的进行,获得的数据不断增加,旧数据的累积对协方差矩阵P的影响逐渐增大,使之趋于稳定,这导致无迹卡尔曼滤波无法快速准确地跟踪参数变化.路面附着系数是时变参数,路面附着系数随时可能发生突变,而在这时新数据比老数据更能反应参数变化的情况.在估计算法中引入遗忘因子可以用来确定数据更新的权重,算法的收敛速度和跟踪速度受遗忘因子的影响[24].对于常遗忘因子f来说,其主要用于决定新老数据的权重,f越小,加强新数据弱化老数据的程度就越强,系统的跟踪能力越强,但是对噪音越敏感,收敛性较差;f越大,加强新数据弱化老数据的程度相对较弱,系统跟踪能力就越弱,对噪声越不敏感,收敛性较好[25].因此常遗忘因子难以快速且准确地追踪路面附着系数这种时变参数.如果能够综合f在较大时的收敛性和f在较小时的跟踪性,那算法的性能就能得到很大的提升.于是本文引入了模糊遗忘因子的概念,通过模糊控制动态地调整遗忘因子的大小,使估计算法在不同情况下都能有较好的收敛性和跟踪能力.

在路面附着系数发生突变时,实际量测向量z=[axωrlωrr]会产生明显变化,实际残差协方差矩阵rk也会产生明显变化,而旧数据的累积使得无迹卡尔曼滤波理论差协方差矩阵Pzkzk趋于稳定,这种情况导致的算法跟踪能力变差,能够通过e(理论差协方差矩阵与残差协方差矩阵之差矩阵的迹)很好地体现出来.但是三个量测变量ax,ωrl,ωrr的量纲不一样,不能直接将方差的偏差相加得到e,因此采用归一化处理对e进行修改.本文采用最大-最小归一化方法对方差进行处理,将方差归一化到区间[0,1]上.

通过仿真和实车试验数据分析可知方差D(ax),D(ωrl),D(ωrr)最小值为0,最大值分别为D(ax)max=9,D(ωrl)max=400,D(ωrr)max=400,从而得到归一化矩阵N,表示如下

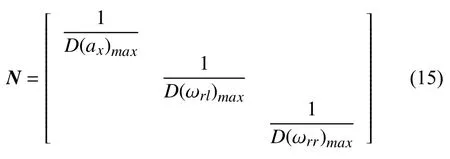
得到归一化后的e,表达式如下

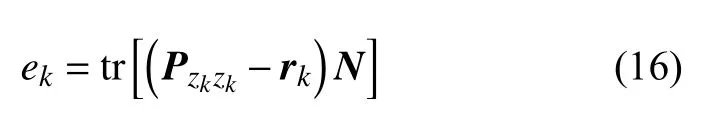
对遗忘因子f模糊控制调节,具体设计如下.

输入量e的模糊论域设定为[-3,3],ec的模糊论域为[-10,10],e和ec的模糊子集均为{NB,NM,ZO,PM,PB}.输出量f的模糊论域为[0.95,1],模糊子集为{LL,LM,M,BM,BB}.模糊控制的隶属度函数如图3 所示.

图3 模糊控制的隶属度函数Fig.3 Membership function of fuzzy control

本文以e及其变化率ec作为模糊控制的输入,输出为遗忘因子f.具体步骤如下.

①输入/输出量的模糊化.

②模糊推理规则设计

当 |e| 较大时,应取较小的f,以提高滤波算法对系统参数变化的跟踪性能.

当 |e| 较小时,应取较大的f,以提高滤波算法的收敛性能和抗噪性能.

当ec·e＜0时,|e| 有减小的趋势,故此时 |ec| 越大应取较大的f.

当ec·e＞0时,|e| 有增大的趋势,故此时 |ec| 越大应取较小的f.

根据以上结论设计模糊规则表如表1 所示.

表1 模糊推理则表Table 1 Fuzzy inference table

③解模糊

利用MATLAB 的fuzzy 工具,选择重心法进行解模糊.常用的解模糊法有最大隶属度法、加权平均法和重心法,由于重心法具有更加平滑的输出推理控制[26],因此采用所示重心法[27]进行解模糊得到遗忘因子f,从而获得修正的协方差矩阵为

式中,ωc为协方差权值,为状态预测值;Q为W的方差矩阵,Q=E(WkWkT),W为系统噪声.

2.2 路面附着系数估计仿真分析

为验证路面附着系数估计算法的有效性,本研究以传统UKF 路面附着系数估计算法为对照组,采用Simulink/TruckSim 联合仿真平台进行对接路面和对开路面仿真试验,对所设计的路面附着系数估计算法的有效性进行验证.

工况一:对接路面工况

设置路面模型为对接路面,车辆从静止开始加速,车辆先进入附着系数为0.75 的高附着路面然后进入附着系数为0.3 的低附着路面,路面附着系数估计结果如下图所示.

由图4(a)和图4(b)可以看出,在估计的初始阶段传统UKF 算法收敛速度较慢且估计偏差较大,在高附着路面上估计最终偏差超过10%,而FFUKF 算法在初始阶段能够在0.5 s 内快速收敛到真实值附近,在高附路面上最终偏差不超过5%.当路面附着系数突然发生变化时,传统UKF 算法不能快速跟踪真实值,在路面附着发生突变近3 s 后估计偏差仍超过50%.FFUKF 算法通过引入模糊遗忘因子能够根据滤波器输出的误差值动态地调整协方差矩阵,估计算法能够自适应地跟踪路面附着系数的变化,结果显示在路面附着系数发生变化的0.5 s 左右FFUKF 算法收敛到真实值附近,在低附路面最终估计偏差不超过5%.

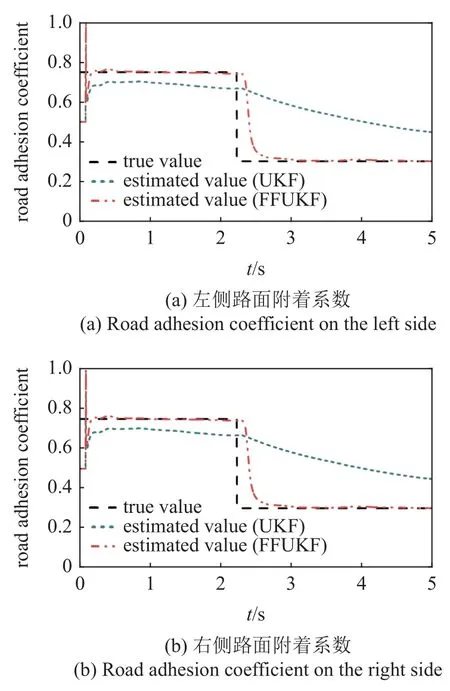
图4 对接路面仿真结果Fig.4 Simulation results of joint road

工况二:对开路面工况

设置路面模型为对开路面,左侧为高附侧,路面附着系数为0.75,右侧为低附侧,路面附着系数为0.3,车辆从静止开始加速,路面附着系数估计结果如图5 所示.

图5 对开路面仿真结果Fig.5 Simulation results of split road

由图5(a)和图5(b)可以看出,传统UKF 算法需要2.5 s 左右才能收敛到真实值附近,且估计误差较大,左侧附着系数最终误差为10%左右,右侧附着系数最终误差为20%左右.而FFUKF 估计算法在0.5 s 内就能够收敛到真实值附近,左、右侧附着系数最终估计误差均小于5%.

3 TCS 控制器

3.1 TCS 基础扭矩

根据上文得到的左右路面附着系数 μl和 μr,计算路面附着所能提供的最大驱动力Ftmax和所需的发动机净输出扭矩TB1为

式中,i0为主减速器传动比,ig为变速器传动比,ηT为传动系统传动效率.

在一般路面上通过路面附着系数 μl和 μr计算得到的基础扭矩TB1较为准确,但当车辆在不平道路上加速行驶时,车轮将会产生振动和轮速波动,这将影响路面附着系数估计效果和基础扭矩TB1的计算准确度,从而降低了TCS 的控制效果.因此针对不平路面驱动工况,本文提出了路面不平参量B的概念,用以表征车辆在当前路面上行驶时路面附着系数估计的准确度.

研究表明路面不平会对轮加速度信号的振动幅值和周期产生影响[28],因此可以设定加速度门限值,记录单位时间内驱动轮加速度穿越此门限的次数,如图6 所示,该方法称为“穿越计次法”[29],单位时间内的穿越次数即为路面不平参量B,具体实现步骤如下.

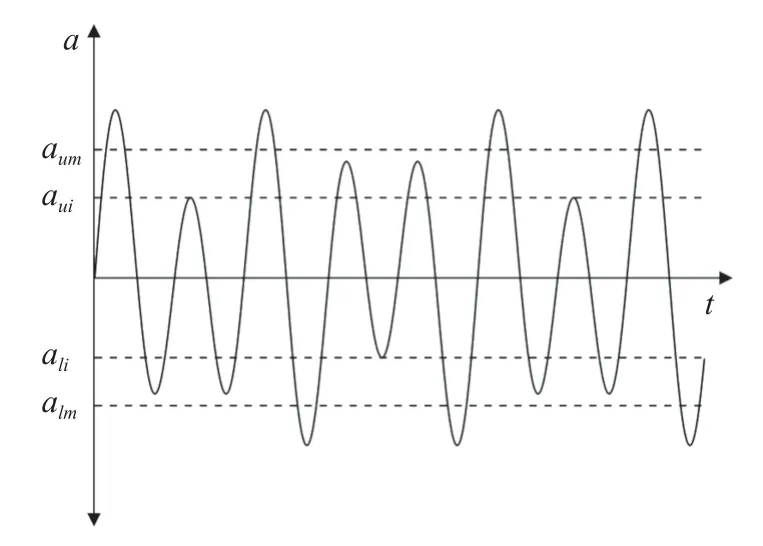
图6 穿越计次法示意图Fig.6 Schematic diagram of traverse method

(1)设定m组穿越门限aui和ali(i=1,2,···,m,au表示上限,al表示下限).

(2)设定m个不平度累加值pi(i=1,2,···,m),驱动轮加速度波动的幅度越大,其能够穿越的门限值越大,每次穿越门限值所加的不平度累加值pi越大.

(3)驱动轮的加速度每穿越一次门限值累加一次pi,记录一定时间T内总的累加值,记为路面不平参量B,B每过T时间更新一次.

由以上可知,在不平路面上路面附着系数估计不准确,这导致基于路面附着系数计算得到的基础扭矩TB1不准确.为解决以上问题,可以驱动轮滑转率在目标滑转率附近时记录此时车辆加速度作为车辆在该路面上的目标加速度,以此加速度计算目标基础扭矩,计算公式如下

式中,ar为目标加速度.

此方法计算的基础扭矩TB2受路面不平影响较小,计算较为准确.但在路面附着系数发生突变,驱动轮滑转率可能不在目标滑转率附近时,此时目标加速度保持上一次的值,没有更新,导致基础扭矩TB2计算不准确.针对以上问题,本文基于可拓控制理论划分经典域、可拓域和非域,通过可拓关联函数得到动态权重系数,将上述两种方法计算得到的目标基础扭矩TB1和TB2进行可拓融合,以提高目标扭矩的准确度.具体实现步骤如下.

(1)特征量的选取

基于上文分析可将路面不平参量B作为一个特征量.另外,当车辆起步,车速较低时,路面附着系数估计算法还未收敛,估计不准确.同时,在低速时轮速传感器误差影响较大,这也会使估计不准确,导致TB1的计算也不准确.而基于轮速加速度计算得到的TB2在低速时较为准确,且反应迅速.故同时选择车速v作为另一特征量,为方便可拓集的划分,将特征量重新定义为v′=.基于以上考虑本文选取的特征量为S(R,v′).

(2)可拓集合划分

可拓集合划分如图7 所示.根据仿真和实车调试选取路面不平度的经典域和可拓域的边界值B1=20,可拓域与非域的边界值B2=40.v′的经典域和可拓域的边界值=0.4,可拓域与非域的边界值=0.7.

图7 可拓集合划分Fig.7 Extension set division

(3)关联函数计算

P0表示当前特征量的值.将P0与原点O相连并延长,直线OP0与经典域边界交于P1,与可拓域边界交于P2.根据可拓理论定义,P0到经典域与可拓域的可拓距为d(P0,〈O,P1〉)和d(P0,〈O,P2〉).可拓距和关联函数的计算公式如下,其中i=1,2

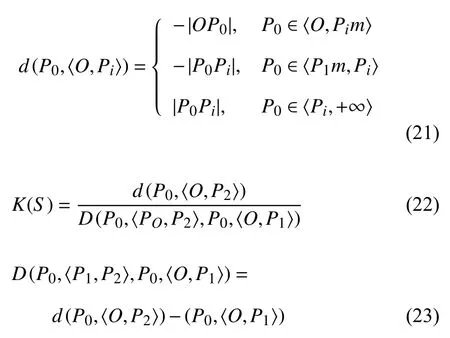
式中,P1m为线段OP1的中点,P2m为OP2的中点.

(4)测度模式判别

测度模式M1:当K(S)≥1时,特征量S(R,v′)在经典域内,路面附着系数估计较为准确,TB1计算准确,所以权重系数 ξ=1.

测度模式M2:当 0＜K(S)＜1时,特征量S(R,v′)在可拓域内,权重系数 ξ=K(S).

测度模式M3:当K(S)≤0时,特征量S(R,v′)在非域内,路面附着系数估计有较大误差,TB1计算不准确,此时基础扭矩采用TB2,权重系数 ξ=0.

(5)基础扭矩计算

根据可拓融合理论,得到的基础扭矩为

3.2 TCS 反馈扭矩

TCS 的设计目标一般是将驱动轮的滑转率控制在0.1～0.2 之间,然而当车辆起步时,由于此时车速很小,轻微的轮速波动会导致滑转率的值出现很大的变化.本文目标驱动轮轮速的设计思路为:车速较低时维持一定滑转量,随着车速增长不断减小滑转量,车速达到一定程度时,再将驱动轮滑转率维持在10%～20%范围内.基于上述分析得到目标驱动轮轮速计算公式如下

式中,vtar为目标驱动轮轮速.

在PID 控制中,微分控制项需要误差的微分,而在实际控制系统中误差的微分往往波动很大,并且会有突变的现象,如果对误差的微分做滤波处理又会产生延迟,失去了微分控制项能够进行“预测控制”的效果.因此在实际工程中有时会摒弃微分控制项,转而采用前馈+PI 控制器,在上节已经介绍了基于前馈思想的基础扭矩设计,因此,PI 控制器更适合本文中反馈扭矩的设计.传统PI 算法参数固定,难以适应复杂多变的情况,模糊自整定控制技术是具有自学习功能的模糊控制类技术[30],模糊自整定PID 控制能通过使用模糊推理实时对PID 控制器的参数进行自整定[31],算法的适应性强.

模糊自整定PI 控制算法中模糊控制以驱动轮轮速误差的绝对值 |E| 为输入,PI 控制的两个参数kp,ki为输出.E为驱动轮目标轮速与实际轮速之差,左、右驱动轮轮速的平均值作为实际驱动轮轮速vact,vact和E的计算如下

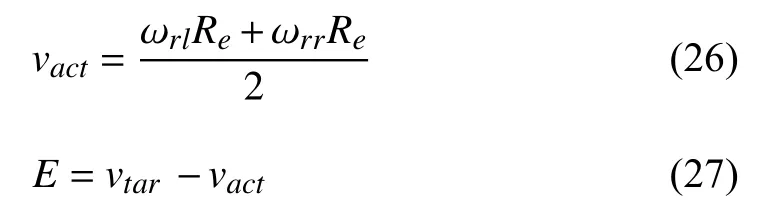
模糊自整定PI 控制具体实现步骤如下.

(1)输入/输出量的模糊化

输入量 |E| 的模糊论域设定为[0,10],模糊子集为{LL,LM,M,BM,BB}.输出量kp的论域为[400,600],模糊子集为{LL,LM,M,BM,BB}.输出量ki的论域为[100,200],模糊子集为{LL,LM,M,BM,BB}.模糊控制的隶属度函数如图8 所示.

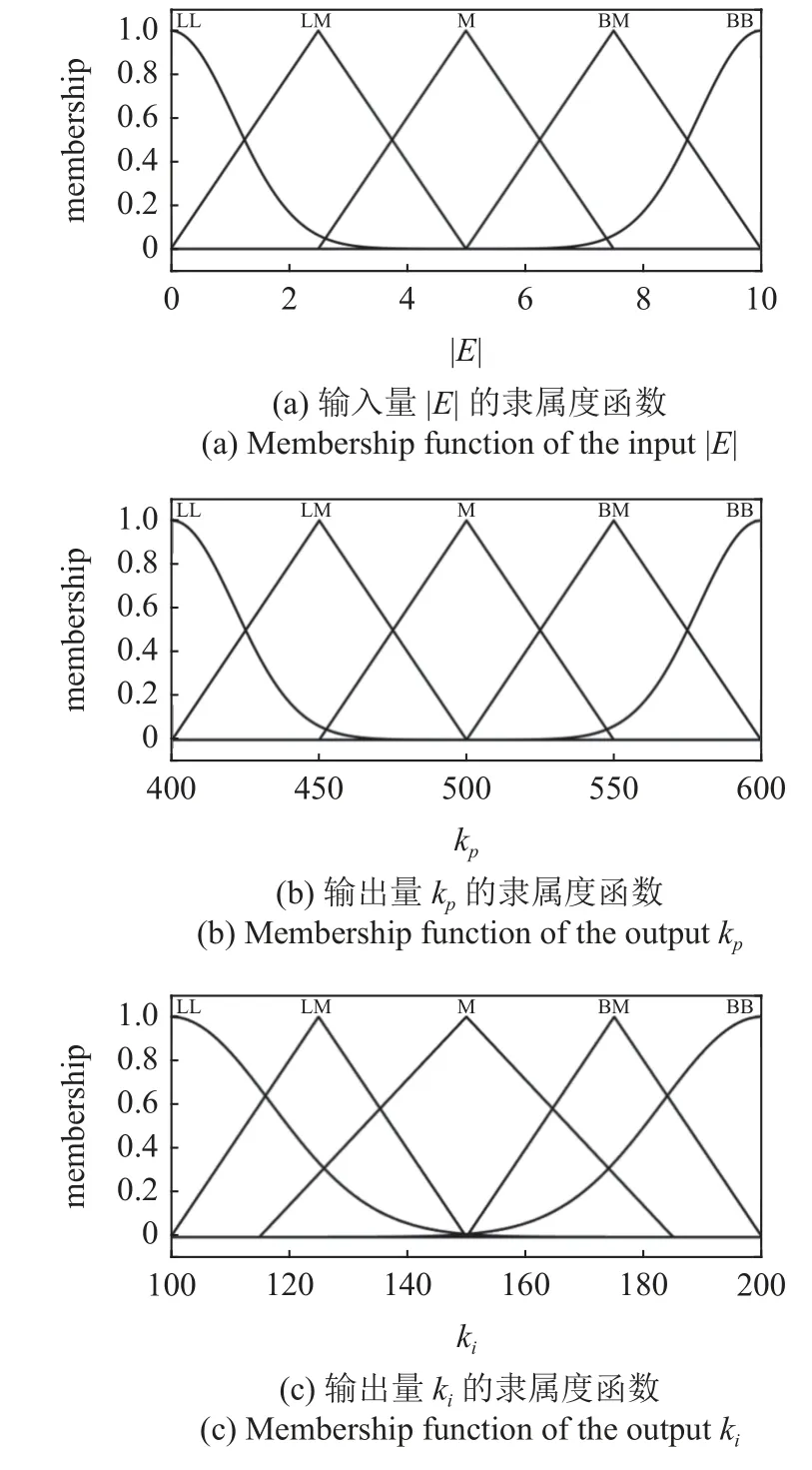
图8 模糊自整定PI 隶属度函数Fig.8 Membership function of the fuzzy adaptive PI

(2)模糊推理规则设计

根据参数kp和ki的作用特点,设计模糊规则如表2 所示.

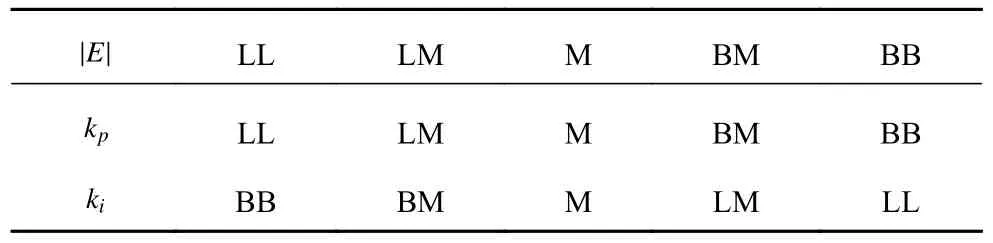
表2 模糊自整定PI 的模糊规则Table 2 Fuzzy rules of fuzzy adaptive PI

(3)解模糊

采用重心法进行解模糊得到kp和ki.

(4)反馈扭矩计算

根据以上得到的PI 控制参数kp,ki计算反馈扭矩,计算公式如下

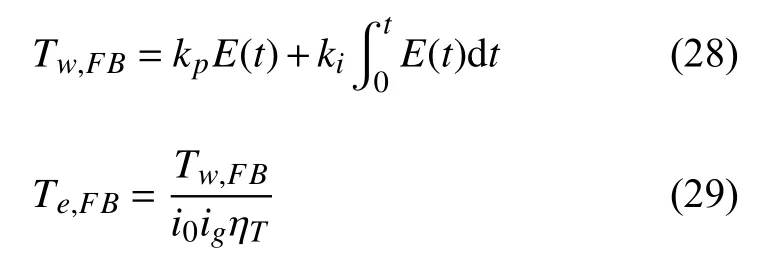
式中,Tw,FB为轮端反馈扭矩,Te,FB为发动机端反馈扭矩.

3.3 制动控制器

本文所设计的制动控制结构框图如图9 所示.TCS 制动压力控制在均一和对开路面上采取不同控制策略.在均一路面上,制动控制的主要作用是保持左右驱动轮轮速一致,因此在均一路面上以左右驱动轮轮速差为输入采用PI 压力控制得到PP,适时的压力控制保证左右驱动轮轮速保持一致.而在对开路面上,由于平衡式差速器平分扭矩到两驱动轮上的特点,这会导致低附侧驱动轮发生较大滑转,而高附侧车轮几乎不滑转,无法充分利用高附侧附着力,因此需要对低附侧驱动轮施加克服两侧附着差的附着差压力Pμ,保证高附着车轮得到充足动力性,同时以左右驱动轮轮速差为输入采用PI 压力控制得到的PP作为补偿制动压力.

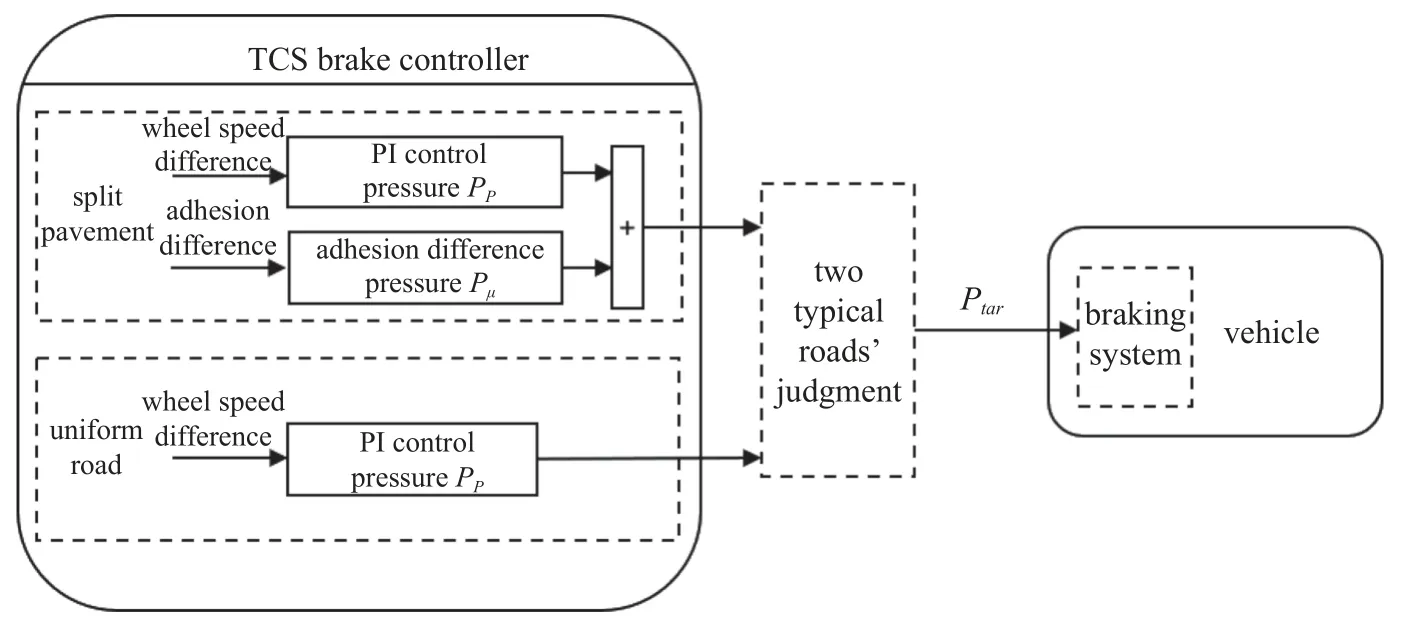
图9 制动控制结构框图Fig.9 Block diagram of brake control structure

(1)压力PI 控制

在所设计的PI 控制器中,输入量为两驱动转速度差,以两驱动转速度差等于零为控制目标,计算公式如下

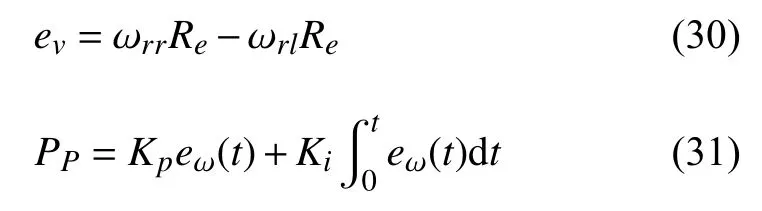
式中,Kp和Ki为PI 控制器的参数.

当Pω＞0 时,说明右侧驱动轮速比左侧快,故对右侧驱动轮施加制动压力Pω,当Pω＜0 时,说明左侧驱动轮速比右侧快,故对左侧驱动轮施加制动压力 -Pω.

(2)附着差压力

对开路面驱动轮受力情况如图10 所示,假设左侧为高附侧,右侧为低附侧.当TCS 扭矩控制介入后,由于降扭控制的作用,高附侧驱动轮不会出现过度滑转的情况,而低附侧驱动轮可能还在滑转,此时高附侧和低附侧驱动轮能够达到最大的轮端驱动力矩,分别为

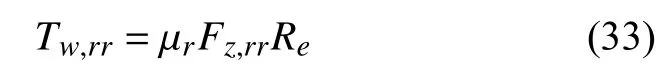
式中,Te,act为当前发动机实际扭矩.

从图10 可以看出,要想高附侧驱动轮达到最大驱动力,充分利用高附侧驱动力,就必须对低附侧驱动轮施加 ΔTw的制动力矩,以克服平衡式差速器的作用,以此制动力矩计算得到的制动压力即为附着差压力,再通过两种典型路面判断即可知道制动力需要作用于哪侧驱动轮上.当然,施加 ΔTw的制动力矩是理论值,在实际情况中可能会因为路面附着估计误差以及发动机扭矩信号误差等导致 ΔTw计算不准确.因此,为了防止过度制动引起的驱动能力和舒适性降低,将在车轮上施加 0.7ΔTw的制动力矩,剩下的制动力可通过PI 控制压力补偿.附着差压力计算公式如下

图10 对开路面驱动轮受力分析Fig.10 Force analysis of drive wheel on split road

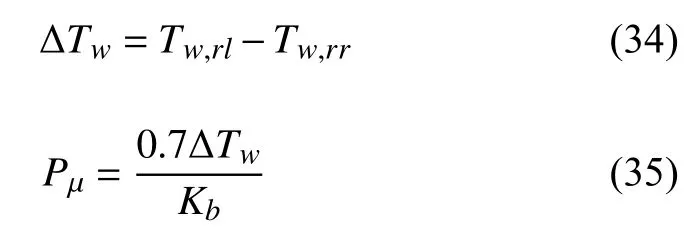
式中,ΔTw为附着差引起的两侧驱动轮扭矩差,Pμ为附着差压力,Kb为制动器系数.

需要说明的是,为了防止制动控制的过度介入,在均一路面上制动控制介入的门限设置为15 kPa.另外,制动控制的精度为10 kPa.

4 实车试验

本次实车试验场地为黑龙江省的北安市极地汽车高寒试验场,设计了均一低附路面、对接路面和对开路面这三种路面试验工况,实车试验所选择的车辆为解放JH6 牵引车头(长宽高为6.165 m×2.495 m×3.91 m),轴数为2,后驱4×2,车辆相关配置参数如表3 所示,其中Pm为发动机最大输出功率,Tm为发动机最大扭矩.试验过程中开启TCS,驾驶员快速踩下加速踏板至100%开度并保持,车辆由静止开始直线加速行驶,换挡逻辑为车辆自身变速器换挡逻辑,从一挡开始自动换挡.

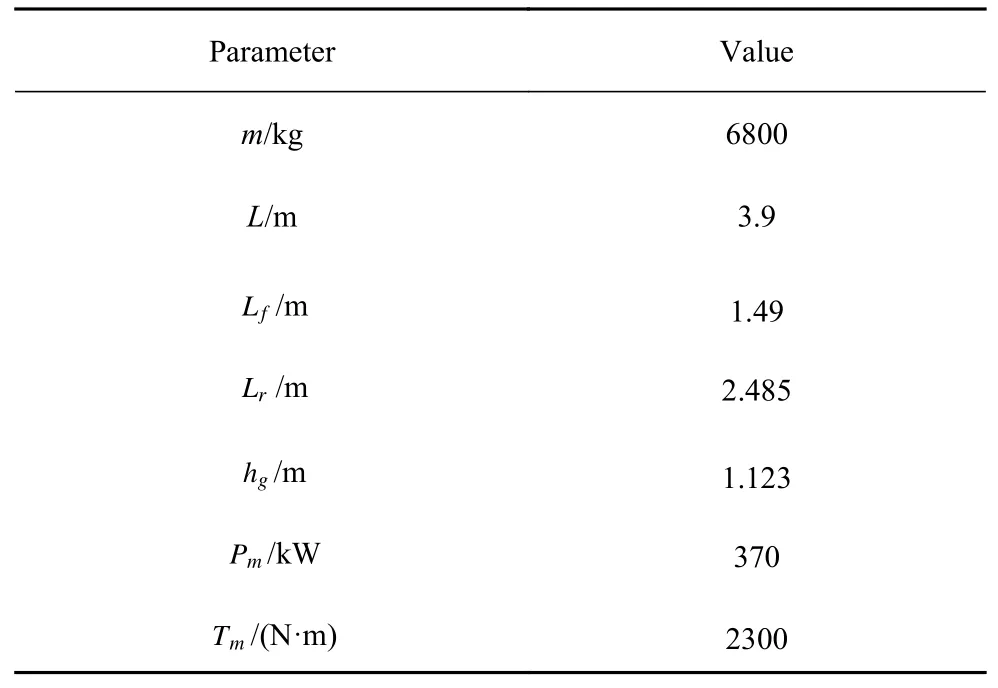
表3 试验车辆参数配置Table 3 Vehicle parameters

4.1 均一路面试验

均一低附路面实车试验结果如图11 所示.从图11(a)可以看出,在车辆速度大于0 后,估计算法开始进行估计,本文所设计的FFUKF 路面附着系数估计算法的估计值能够在1 s 内快速收敛到0.2 左右并保持稳定,其估计值在冰面路面附着系数参考值为0.1～0.25 内,说明本文设计的算法能够快速和准确地对路面附着系数进行估计,为TCS 控制算法提供了有力的支持,提高了TCS 控制效果.

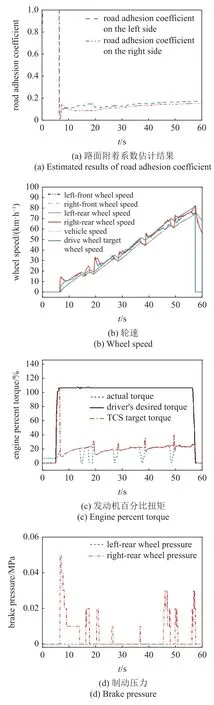
图11 均一低附路面实车试验结果Fig.11 Real vehicle results on the uniform road with low road adhesion coefficient

结合图11(b)～图11(d)可以看出,在5 s 左右车辆开始起步,此时驱动轮还未出现过度滑转,TCS 未介入,TCS 目标扭矩为驾驶员期望扭矩,2 s 后右后驱动轮出现过度滑转,7 s 左右TCS 系统开始介入,立即进行了降扭控制,驱动轮滑转程度迅速减小.同时,制动控制适时进行单侧驱动轮制动,使左右两侧驱动轮轮速保持一致.在10 s 到20 s,30 s,40 s 和50 s 左右驱动轮轮速并不能很好地收敛到目标值附近,这是由于在起步加速阶段换挡导致的,商用车发动机扭矩大,离合器分离时驱动轮失去动力导致驱动轮轮速下降至车速附近,离合器结合时产生冲击造成驱动轮轮速突然增大和波动,但是在整个控制过程中驱动轮并未出现过度滑转和过大的轮速波动.除去换挡阶段,TCS 能够将驱动轮轮速控制在目标值附近,整个过程中平均加速度为0.4m/s2左右,车辆有较强的加速能力,TCS 控制效果良好.

4.2 对接路面试验

对接路面实车试验结果如图12 所示.从图12(a)可以看出,在车辆速度大于0 后,FFUKF 估计算法开始进行路面附着系数估计,在1 s 内左右两侧附着系数估计值达到0.5 左右,7.5 s 时收敛到了0.7 左右,由于车辆在高附路面时驱动轮滑转率非常小且车辆进行换挡导致识别速度较慢,准确度不够高.但是本文路面附着系数算法主要用于TCS 控制,在驱动轮滑转率非常小时TCS 未介入,另外TCS 基础扭矩通过可拓融合得到,并非只依赖于路面附着系数,因此这对TCS 控制影响较小.在10 s 左右车辆驶入低附路面,FFUKF 算法能够快速准确地跟踪路面附着系数的变化,2 s 内快速收敛到冰面附着系数参考值附近且保持稳定.

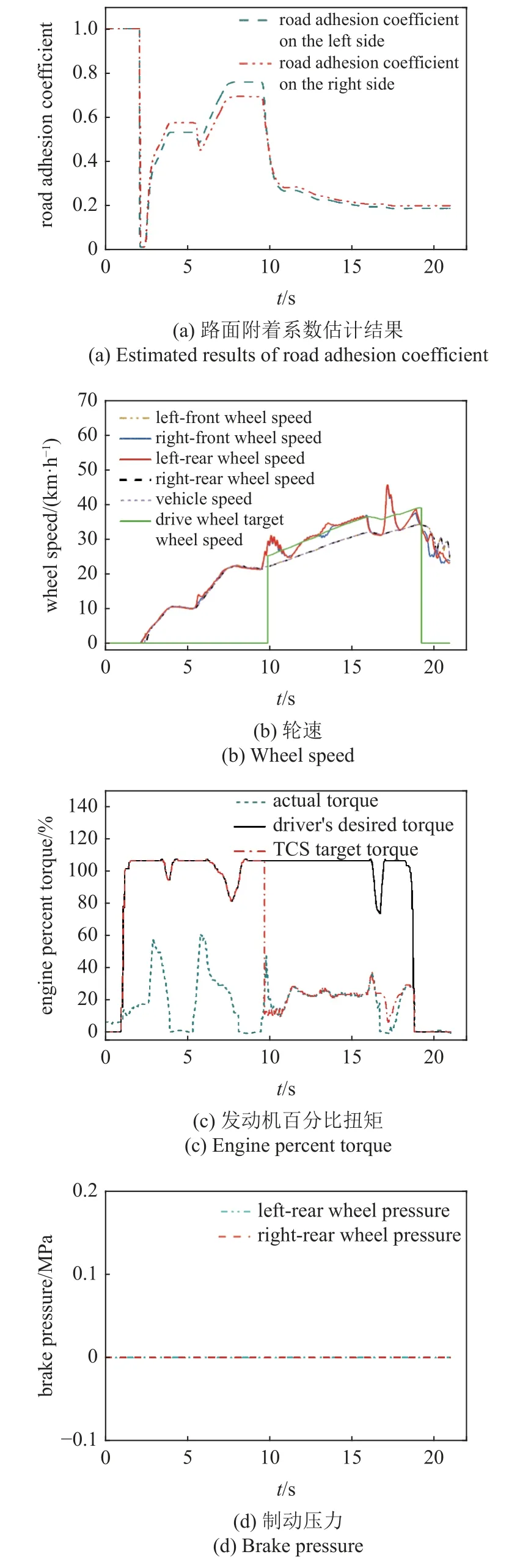
图12 对接路面实车试验结果Fig.12 Real vehicle test results on joint road

结合图12(b)～图12(d)可以看出,在2 s 左右车辆开始起步,驾驶员期望扭矩快速上升,10 s 之前车辆行驶在高附路面上,驱动轮并未出现过度滑转,TCS 未介入,TCS 目标扭矩为驾驶员期望扭矩.在10 s 左右车辆由高附路面行驶至低附路面,驱动轮出现过度滑转,此时TCS 迅速介入,立即进行了降扭控制,在13 s 左右驱动轮轮速被控制在目标轮速附近.同样地,在10 s,17 s 和18 s 左右由于换挡的原因出现了轮速的突然增大,在TCS 的控制下驱动轮轮速很快降了下去,但是由于过度降扭导致17～19 s 左右驱动轮轮速并不能很好地收敛到目标值附近,这是需要优化的方向之一.总的来说在对接路面上TCS 能够在驱动轮出现过度滑转时迅速介入抑制驱动轮的滑转,在冰面加速阶段车辆的平均加速度为0.37 m/s2左右,车辆加速能力较强,TCS 控制效果较好.

4.3 对开路面试验

对开路面实车试验结果如图13 所示.从图13(a)可以看出,在车辆速度大于0 后,估计算法开始进行估计,左侧车轮在水泥石板路面上,本文所设计的FFUKF 估计算法在1 s 内达到0.4 左右,在之后10 s内收敛到石板路面附着系数参考值0.75～0.85 左右,高附侧估计值收敛速度较慢,原因是高附侧驱动轮滑转率非常小且车辆进行换挡导致估计速度较慢,准确度不够高,这是算法优化方向之一.右侧车轮在冰面上,估计值在2 s 内收敛到冰面附着系数参考值0.1～0.25 附近,估计快速且准确.

结合图13(a)～图13(c)可以看出,在2 s 左右车辆开始起步,驾驶员期望扭矩快速上升,此时驱动轮还未出现过度滑转,TCS 未介入,TCS 目标扭矩为驾驶员期望扭矩,之后2 s 内实际扭矩增大,右后驱动轮出现过度滑转,4 s 左右TCS 开始介入,立即进行了降扭控制,驱动轮滑转程度迅速减小,TCS 制动控制持续对右侧车轮施加制动压力,以保证高附侧驱动轮能够充分利用路面附着,当进行换挡时,两侧驱动轮失去了动力,故此时不进行制动.综合来看,TCS 通过扭矩控制和对低附侧车轮进行制动控制抑制了驱动轮的过度滑转,整个过程中车辆的平均加速度为0.6 m/s2左右,提高了车辆的动力性,控制效果较好.

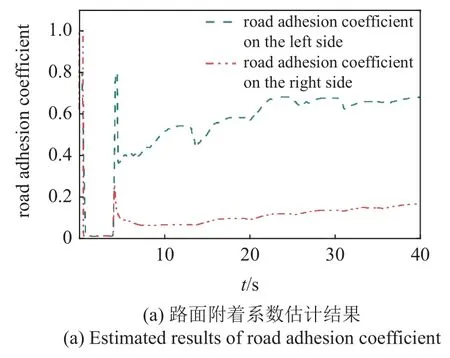
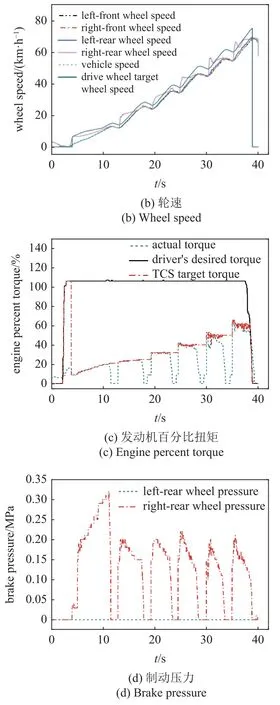
图13 对开路面实车试验结果Fig.13 Real vehicle test results on split pavement

5 结论

本文以后驱牵引车为研究对象,设计了基于路面附着系数估计的牵引力控制系统.

(1)在影响牵引力控制的路面附着系数估计方面,设计了基于遗忘因子的无迹卡尔曼滤波估计算法,通过模糊控制动态地调整遗忘因子的大小,解决了传统无迹卡尔曼滤波无法快速跟踪时变非线性系统的问题.

(2)TCS 扭矩控制器采用基础扭矩加反馈扭矩控制的设计思路.在TCS 基础扭矩设计方面,通过可拓融合将两种计算基础扭矩的方法进行加权融合计算,提高了基础扭矩计算的准确性.

(3)TCS 制动控制器在均一和对开路面上采取不同的压力控制策略.在均一路面上,以两侧驱动轮轮速差为输入利用PI 控制算法得到均一路面目标制动压力,控制左右两侧驱动轮轮速保持一致;在对开路面上,利用路面附着系数和发动机当前扭矩计算附着差压力,以两侧驱动轮轮速差为输入利用PI 控制计算补偿压力,两者相加得到对开路面目标制动压力.该方法提高了制动控制的准确性,防止制动控制过渡介入,提高了舒适性.

(4)实车试验结果表明路面附着系数估计算法在不同路面状态下收敛迅速,估计结果较准确,满足TCS 控制使用要求,提高了TCS 控制效果;在三种路面状态下TCS 控制都能够有效地提高车辆的动力性和横向稳定性,控制效果良好.