基于Cardinal样条的车道偏离预警测评关键参数估计

李宏海，陆红伟，卢立阳，徐启敏

(1.交通运输部公路科学研究院，北京 100088;2.东南大学 仪器科学与工程学院，江苏 南京 210096)

0 引言

智能车路系统(Intelligent Vehicle and Infra Structure System，IVIS)是目前交通领域的科技前沿，是为了实现车车和车路全方位多角度的协同互动，从而提高行车和行人安全，减少交通事故的发生和提高道路通行效率。为了有效实现上述目标，智能车路系统采用了先进的通信技术和全时空高度统一的多传感器融合采集技术等，能够对道路和车辆信息进行高精度实时可靠的信息采集和融合通信，对保障道路安全和提高出行效率具有十分重要的意义。当前欧美日等发达国家均在实施和推进IVIS发展的相关行动计划，我国智能汽车和智能路侧设备等产业也发展迅速[1-3]。

先进驾驶辅助系统(Advanced Driver Assistance System， ADAS)是智能车路系统的重要组成部分，对于智能车路系统的发展具有十分重要的意义，目前也被广泛应用于各种车辆上。ADAS是利用安装于车辆端的各种传感器进行车辆行驶过程中环境的感知和数据采集分析，如利用卫星导航进行车辆实时高精度的定位，利用惯导进行车辆姿态的识别和速度、加速度的采集，利用雷达(毫米波雷达、激光雷达等)和摄像头进行环境的感知和监测等，然后将这些传感器信息进行融合处理后，进行系统化分析处理，给出合理的驾驶建议，提高驾驶的安全性和舒适性。据维基百科的定义，ADAS包括自适应巡航、车道偏离预警系统、车道保持系统等在内的多个系统及功能。本研究主要研究车道偏离预警系统(Lane Departure Warning System,LDWS)，在车辆行驶过程中，LDWS会利用相关传感器(如摄像头等)实时监测车辆与车道的相对位置情况，当检测到车辆偏离车道并且有一定的危险时，会采取相应的音视频手段提醒驾驶员，为其提供充足的反应时间。车道偏离预警系统能够极大地提高行车安全，减少因驾驶员疲劳驾驶从而导致车道偏离乃至发生交通事故的风险，在智能车路系统中具有十分重要的地位和意义[4-6]。

目前国内外针对LDWS均进行了相关研究。在国外，许多发达国家都投入大量资金以及人才进行LDWS的研究，比较具有代表性的LDWS有美国卡内基梅隆大学研发的AURORA系统，该系统采用车载高性能工作站进行图片的实时处理，最大处理速率达60 Hz以上，能够很好地满足车辆行驶中对于预警系统实时性的需求[7-8]；美德两国联合研发了AutoVue系统[9]，该系统主要面向营运卡车并获得实际应用，获得了较好的社会效益和经济效益；荷兰研发了Mobileye_AWS系统[10]，该系统相对于其他系统优点突出，既可以用于结构化道路的车道线检测和车道偏离预警，也可以用于没有车道线的非结构化路面，利用车道的路肩来判断车辆的位置；日本三菱汽车公司设计和研发了DSS，并在模型车上进行实际工况应用[11]，在国际上获得了诸多安全奖项。在国内，近些年来针对LDWS的研究也很多，如清华大学智能技术与系统国家重点实验室研制的“THMR-V”智能车[12]，浙江大学针对自主智能车辆引进的分布式测试系统IVD (Intelligent Vehicle Detection-bed)[13-14]，国防科技大学研发的CITAVT系列智能车[15-16]，吉林大学开发的JLUVA-1系统[17-18]和由东南大学基于DSP技术开发的车道偏离报警系统[19-20]，除此之外国内其他一些科研单位和高校在LDWS方面的研究也在如火如荼地进行中。

当前，虽然包括LDWS在内的先进驾驶辅助系统发展迅速，各个汽车厂家均推出了高智能度辅助驾驶的汽车产品，但近年来不管是特斯拉、谷歌还是Uber等都出现了很多交通事故，而且Uber还在2018年3月发生了第1起自动驾驶汽车致死事故。这些都说明当前在大力发展高智能ADAS的同时，对系统的测试和评价也至关重要，如何科学地判别智能汽车的安全性和可靠性，也是当前面临的一个重要问题。对于车道偏离预警系统(LDWS)的测评，目前我国已有标准《智能运输系统 车道偏离报警系统 性能要求与检测方法》(GB/T 26773—2011)，但在该标准中仅列出测评场景及流程，未给出车道线距离等测评指标的具体计算方法，在实际应用中，依然会遇到计算方法不明、指标不够定量化等问题。因此，对于LDWS的测评，亟需一种行之有效的测评方法和测评指标。

针对上述问题，本研究提出了一种基于Cardinal样条的车道偏离预警测评关键参数估计方法。该方法首先利用高精度差分组合导航分别从车道线以及测试车辆上获取测评所需基础参数数据，然后对采集到的车道线坐标进行Cardinal样条拟合，从而提高车道线的测量精度，减小测评误差；在得到高精度车道线的基础上，利用车道线信息和车载采集信息，结合牛顿迭代算法，进行关键参数的解算。

1 基础参数采集

精确的基础参数采集是进行LDWS测评的基础，本研究采用基于GNSS/INS的组合导航系统来实现位置、速度等基础参数信息的准确采集。

1.1 全球导航卫星系统

全球导航卫星系统(Global Navigation Satellites System，GNSS)是以接收和播发电磁波信号来达到导航、定位、授时(简称PNT)的目的。其依赖于高轨道的卫星播发的导航电文和载波信号，在大地测量、车联网、自动驾驶等领域发挥着重要作用。

长期以来，一直以美国的GPS为代表的卫星导航具有全天候、全天时的优势。随着欧盟Gallieo、俄罗斯GLONASS以及中国BDS的发展，多频率、多系统的卫星导航定位已经成为现实。就目前而言，卫星导航的发展已久，前景无量，尤其是以北斗3组网完成为标志，研究北斗与其他GNSS的组合，在我国具有非常重要的意义和价值。

除此之外，卫星导航高精度定位已经成为现实，如发展相对成熟的RTK技术、PPP技术等，相对于其他导航系统的优势在于误差不会随着时间累积。但是其研究也存在瓶颈，如PPP技术不能快速收敛、模糊度固定问题、复杂环境下信号缺失问题、模糊度重固定问题、高精度的动态定位问题等，而这些问题就目前而言仅仅依赖卫星导航是基本不可能得到有效解决的，因此需要将卫星导航同其他导航系统相结合，来弥补GNSS卫星导航的先天性不足。

1.2 惯性导航

惯性导航系统(Inertial Navigation System，INS)是一种相对独立自主的导航系统，不与外界发生任何信号交换便可完成导航和定位。随着计算机技术的发展，基于捷联技术的惯导因具有结构简单等优点，逐步取代了平台式惯导，成为目前应用最广泛的INS，简称SINS。

由于惯性导航自身的独特性质，使其在定位过程中的误差会随着时间逐渐累积，单靠INS完成长时间导航定位的结果是非常不可靠的，因此其并不具备高精度的长期导航定位的能力。

1.3 GNSS/INS组合导航

综上所述，GNSS和INS各有优缺点，但同时能够优势互补，因此目前多将其进行组合使用，这对于提高导航性能和精度有着重要的意义，其优势主要体现在：

(1)可以对惯性导航系统误差进行估计和校正，提高组合导航精度；

(2)可以弥补卫星导航信号缺损问题，提高组合导航能力；

(3)可以提高卫星导航接收机对卫星信号的捕获和跟踪能力，提高整体导航效率；

(4)可以增加观测信息冗余度，提高系统容错能力；

(5)可以提高导航系统的抗干扰性，提高组合导航的完好性。

根据应用要求及参与组合观测量的深度，GNSS/INS组合的模式可分为松组合、紧组合和深组合。3种组合模式的对比示意图如图1所示，从图中可以直观地区分3种组合模式的层次。

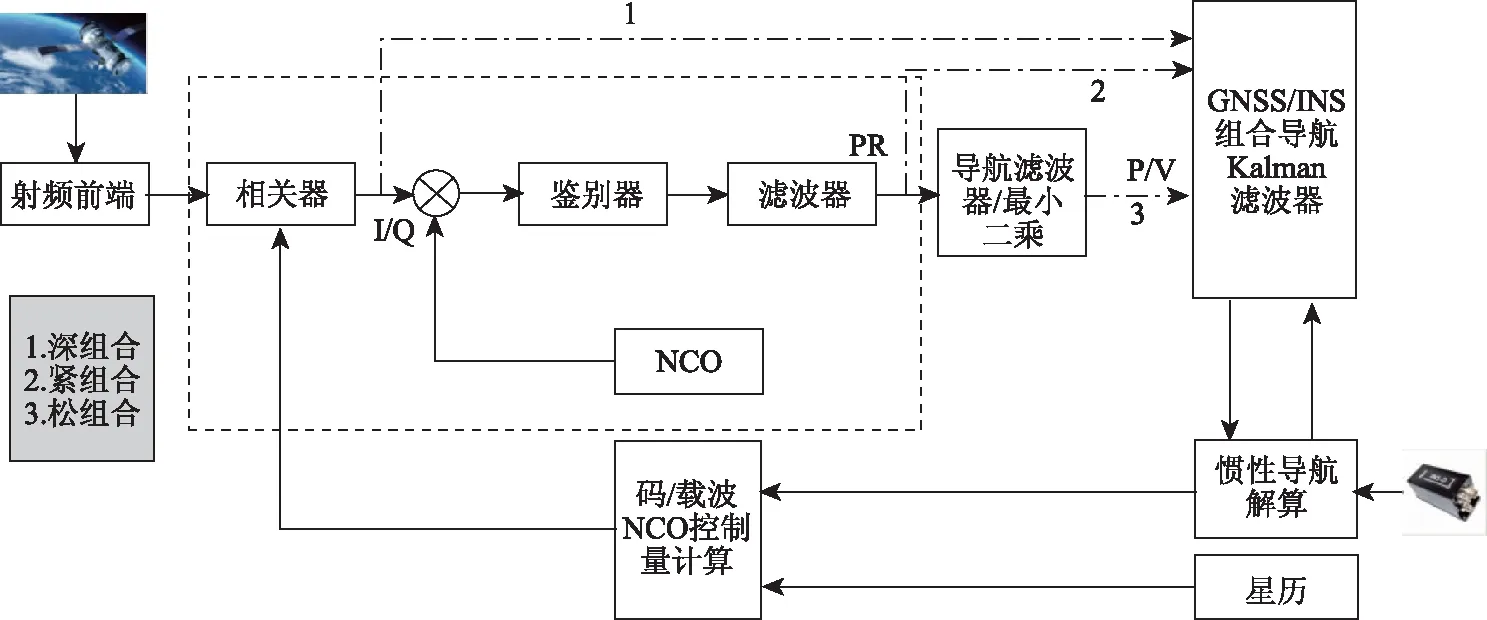
图1 GNSS/INS组合示意图

在图1中，分别用1，2，3代表深组合、紧组合和松组合。对于松组合来说，是利用GNSS接收机输出的位置、速度信息和INS输出信息进行组合，两者共用1个滤波器进行数据融合。由于GNSS接收机的导航解是作为观测量输入滤波器的，所以GNSS接收机必须能够同时捕获并跟踪到4颗以上的卫星才能获得导航解。因此，在GNSS信号遮挡或受干扰时，系统在INS独立导航的状态下，长时间工作会导致导航精度有所降低。与松组合不同，紧组合是利用GNSS接收机输出的伪距、伪距率等观测量，与INS结合星历反算得到的伪距、伪距率进行组合。这种参与组合的方式，使得GNSS接收机输出了原始信息进行参与组合，伪距和伪距率这些基本观测量的相关性低，从而具有较大的优势，一方面可以在卫星少于4颗时正常工作，另一方面定位的精度相比于松组合也得到了较大的提升。上述松组合和紧组合两种组合模式本质上都是利用GNSS接收机的输出信息来辅助INS，在解算的过程中，GNSS接收机依然保持独立，因而接收机本身的抗干扰能力并未得到本质的提升。

针对上述两种组合方式存在的不足，近年来又开发了一种新的组合模式：深组合，是一种深层次的、涉及到硬件层面的组合模式。从图1中可以看出，与前两种组合模式相比，深组合取消了独立不相关的码和载波跟踪环路，直接将相关器输出的I/Q数据作为输入信息，输入到组合导航的卡尔曼滤波器中，然后将融合后的信息控制调整码/载波数控振荡器(Numerical Controlled Oscillator，NCO)。从信息处理流程分析可知，相关器输出的I/Q信息在理论上满足观测噪声相互独立的特性，因此深组合模式具有理论上的“全局最优”特性。深组合模式便于GNSS接收机与INS进行一体化设计，实现了GNSS接收机和INS两者之间的相互辅助，可以降低对INS的精度要求以及组合导航系统的成本和体积，这也为IMU参与高精度组合提供了可能。3种组合模式的性能比较如表1所示。

表1 不同组合模式性能比较

本研究基础参数采集中使用的算法即为上述深组合算法，为车道偏离预警测评提供精准的位置、速度、航向角等信息。

2 Cardinal样条车道线拟合

利用上述组合导航系统进行道路基础位置坐标的采集之后，由于采集到的点较为稀疏，无法准确表征道路的实际情况，因此还需要利用拟合算法对车道离散点进行插值拟合，从而更好地估计车道线的参数信息，为后续的测评参数解算打下良好的基础。在此采用Cardinal样条对离散车道坐标点进行拟合。

2.1 Cardinal样条车道线拟合模型

采集得到的某段独立道路轨迹数据为T={T0(c0,z0),T1(c1,z1),…,Tn(cn,zn)}，其中，cn，zn分别为道路轨迹点的北向位置坐标和东向位置坐标;n为轨迹数据点的个数。

利用Cardinal样条曲线对组合导航采集到的轨迹数据进行插值，样条曲线受坐标集T中的控制点控制，独立的单侧车道数据块中，除去两端的控制点T0(c0,z0)，Tn-1(cn-1,zn-1)，Tn(cn,zn)后，对剩余的n-3个控制点，三次Cardinal样条曲线可由任意4个连续控制点确定。设P(u)是两控制点Tk和Tk+1间的拟合曲线的三次函数式，其中u为参变量，0≤u≤1；k=2,3,…,n-2；则取从Tk-1到Tk+2间的4个控制点用于建立拟合车道线的边界条件：

P(0)=Tk，

(1)

P(1)=Tk+1，

(2)

(3)

(4)

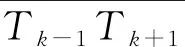
将上述边界条件转换成矩阵形式为：

(5)

其中Cardinal矩阵为：

(6)

式中，s=(1-t)/2。

将上述矩阵方程展开成多项式形式，则有：

(7)

进一步将Tk-1，Tk，Tk+1，Tk+2分解成二维平面上x，y方向上的分量，得到控制点Tk，Tk+1之间的曲线段的参数三项函数式在x，y方向上的表达式如下：

(8)

展开后按u的升幂排列，得到控制点Tk，Tk+1之间的三次Cardinal样条曲线参数形式如下：

(9)

式中参数如下：

(10)

定义参数矩阵：

(11)

经由上述过程，得到了独立的单侧车道数据T1(c1,z1)到Tn-2(cn-2,zn-2)之间，经过三次Cardinal样条插值的车道线拟合方法，曲线参数集合Q=(t,Y2,…,Yk,…,Yn-2)，其中t为张量参数，k=2,3,…,n-2；由于Cardinal样条法生成的曲线必定经过原始控制点，因此利用高精度的车道线位置信息便可以精确地反映出车道线的位置与形状；对于具体的原始车道位置数据，可由u在[0,1]上的取值步长控制每段(两个控制点之间)的插值个数，由t控制每段(两个控制点之间)的曲线松紧程度，可以形成任意形状的曲线，来满足特定路段的控制要求与精度要求。

2.2 Cardinal样条车道线拟合性能评价

为了充分验证本研究所提出的车道线拟合算法的有效性和通用性，选择一段实际的直道弯道组合的道路进行试验。首先利用第1节所述的组合导航系统进行车道线位置点的采集，共采集40个离散的路径点，如图2所示。

图2 离散路径点采集

然后建立三次Cardinal样条曲线，对上述离散车道线进行拟合插值，为了充分验证算法的优势，将其与常用的Hermite样条曲线的拟合结果进行对比，得到的拟合结果如图3所示。从平均位置误差和算法时间两个维度来评判算法的有效性，具体比较结果如表2所示。从图3和表2中可以看出，在拟合的效果上Cardinal样条要明显优于Hermite样条，并且有着更快的拟合速度。

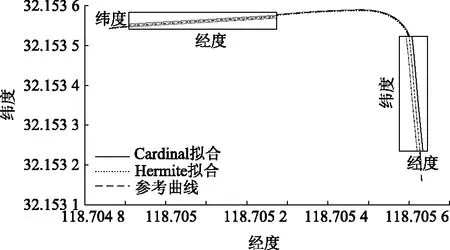
图3 车道线拟合结果

表2 不同样条函数拟合结果对比

3 关键参数估计方法

3.1 基础参数预处理

对于车道偏离预警测评场景，车道偏离的界定标准为车辆前轮的外缘是否将要超出车道边线，而组合导航系统记录的车辆位置实际为系统主天线的位置，因此需要先将记录的主天线运动轨迹转换成主车(Host Vehicle,HV)前轮的运动轨迹，其过程如下：

假定该时刻为tc，tc时刻对应的经纬度坐标为(xc,yc)，若组合导航信息的采集时刻没有tc的对应值，可采用线性插值计算得出经纬度坐标为(xc,yc)，xc为纬度，yc为经度；若进行插值操作，其余测量参数也应进行插值处理。然后将其转换为高斯投影坐标(xu,yu)(东向位置、北向位置确定的平面投影坐标系)。

如图4所示，假设主天线安装在HV中轴线上，与两前轮外缘处的纵向距离为d，横向距离为L，车辆航向角为H，H∈[0,360°]，定义北向为起始方向，顺时针方向为正，由图4可得：

图4 车辆前轮位置解算

(12)

β=π-α，

(13)

(14)

d3=d1·cosβ，

(15)

d4=d-d3，

(16)

d2=d4·cosβ，

(17)

式中，α是车辆航向与正东的夹角；β是α的补角；d1，d2，d3，d4是车辆的几何参数。

局部切平面直角坐标系坐标左前轮外缘处的位置坐标Pl为：

(18)

类似的，可以根据几何关系计算出右前轮外缘处的位置坐标Pr：

(19)

对组合导航系统中记录的HV位置均作以上处理，即可得到任意时刻HV前轮外缘的运动轨迹。

3.2 车辆与车道线的距离解算

车道偏离预警测评过程中，采用横向距离来衡量车辆与车道线的距离，以上一节中计算所得的两前轮外缘位置作为该特定部位，分别计算与两侧车道边界的距离，以左侧车轮外缘为例，计算过程如下：

假定该时刻仍为tc，局部切平面直角坐标系坐标左前轮外缘处的位置坐标已知，为Pl；左侧车道线拟合C1上，Pl位于控制点Tc和Tc+1之间确定路段的横向区域内，该路段对应拟合曲线为：

(20)

式中，s=(1-t)/2；其本质上对应1个关于u∈[0,1]的多项式：

考虑到拟合实际车道线的情况下，两控制点Tc和Tc+1之间拟合曲线斜率变化不大且较平缓，用点Pl到三次曲线P(u)的最短距离代替横向距离，采用求解速度较快的牛顿迭代法求解：

设点Pl到曲线P(u)的距离为D(u)，

(D(u))2=|Pl-P(u)|2=

[xl-P(u)x]2+[yl-P(u)y]。

(22)

为求解min(D(u))2,u∈[0,1]，即求解(D(u))2在[0,1]上的极小值，问题转化为求极值问题。(D(u))2的极值出现在其导数值为0的点，即：

2[xl-P(u)x]P(u)′x+2[yl-P(u)y]P(u)′y=0。

(23)

令：

f(u)=2[xl-P(u)x]P(u)′x+2[yl-P(u)y]P(u)′y，

(24)

(25)

用牛顿迭代公式求解：

(26)

选取曲线边缘u=0或u=1为初值进行迭代计算，得到的距离偏差D(uk+1)-D(uk)<0.02 m时停止迭代，取uc=uk+1，时刻tc对应的距离为D(uc)，特别的，当车辆轮胎外缘位于车道边界线外侧时，车辆与车道线距离D取负值。

3.3 偏离速度解算

车道偏离预警测评过程中，假如twarn时刻车道偏离报警被触发，此时HV接近车道边界的速度的垂直分量定义为偏离速度，以左偏情况为例，计算过程如下：

局部切平面直角坐标系下，twarn时刻车辆左侧附近车道线斜率为kwarn，kwarn由距离计算过程中迭代得出的插值点P(uk+1)处的切线斜率确定，车道线切线对应角度为：

θ=arctan (kwarn)。

(27)

此时HV航向角为H，对应角度为：

(28)

此时HV速度为v，对应偏离速度为：

(29)

4 试验验证

针对上述提出的车道偏离预警测评关键基础参数解算方法，利用实际测试数据进行解算验证，以评价车道偏离预警有效性为例。

实际测试过程中，无论HV系统内部如何设置报警触发点，报警临界线都应位于最迟报警线内侧，因此选用最迟报警线作为偏离预警及时性的测评基准。设最迟报警线位于车道边界线外侧距离为dlast处(乘用车dlast取0.3 m；商用车dlast取1 m)，当HV有向车道边界线偏离的趋势时，该趋势会反映在车辆与最迟报警线距离Dd、偏离速度vd和预计越界时间tcross的变化上，通过为其设定界限值分别可测评本次测试的有效性与预警情况的有效性。假定安全情况下车辆轮胎外缘与最迟报警线距离下限为D0，偏离速度上限为v0，预计越界时间下限为t0，界定条件如下：

Dd=D+dlast

(30)

(31)

(32)

当预警时刻偏离速度vd、预计越界时间tcross满足上述条件时，可认定本次测试是有效的，即HV在测试中发生了偏离；在测试有效的前提下，HV偏离车道时，当车辆位于临界报警线之外时，系统应持续报警，即当HV与最迟报警线距离Dd

试验测试所得结果如图5所示，图中实线为利用采集的基础数据拟合后的车道线，虚线为车辆行驶轨迹，五角星为标注的预警点。根据上述提出的计算方法，分别利用Cardinal样条和Hermite样条进行车道线的拟合，计算车道偏离预警时车辆位置与车道线的距离，并与实测真值进行对比，结果如表3所示。表中，Cardinal样条和Hermite样条分别利用40个简化后的离散路径点拟合曲线，再分别计算车道偏离预警发出时的车辆位置与拟合曲线的距离；真值为车道偏离预警发出时的车辆位置与4 000个原始路径点的最短距离。可以看出，相对于Hermite样条，Cardinal样条拟合后的计算结果更加准确。

图5 实际测评结果

表3 关键参数解算结果对比

同时利用上述计算方法计算可得vd为1.28 m/s，tcross为0.21 s。这也验证了本研究所提出的测评方法可以准确测量出测评所需关键参数，为开展定量化测评和判断测试结果提供准确依据。

5 结论

本研究首先分析了当前智能驾驶及车道偏离预警系统测评的必要性，指明了当前缺乏有效的测评方法和指标的现状。然后，提出了一种基于Cardinal样条的车道偏离预警测评关键参数估计方法，该方法首先利用高精度差分组合导航分别从车道线以及测试车辆上获取测评所需基础参数数据，然后对采集到的车道线坐标进行Cardinal样条拟合，并且与Hermite样条拟合方式进行对比，拟合精度和速度均优于后者。在得到高精度车道线的基础上，利用车道线信息和车载采集信息，结合牛顿迭代算法，进行关键参数的解算。