基于粒子群算法的单壁钢围堰加固施工优化

钟正强，刘卓泽，彭建新，陈敬智

(长沙理工大学 土木工程学院,湖南 长沙 410114)

0 引言

近年来，我国的深水大跨桥梁建设取得一系列重大突破，与陆地桥梁不同，深水大跨桥对墩台基础施工提出了更高的要求。单壁钢套箱围堰作为一种高效能的阻水结构，被广泛应用。它一般适用于水深6～10 m范围内，其整体性强，分块装配简单，便于循环使用[1]。目前，单壁钢套箱围堰在低桩承台施工[2]、旧桥桥墩加固[3-4]等方面应用较为广泛。但是，当它被应用于深水基础施工时，就会出现用钢量大、安全风险高、造价提升等问题，这些问题聚焦在围堰抽水施工工况。在该工况下，单壁钢围堰结构最不稳定，安全性能差，是控制围堰结构设计关键的一环。因此，在抽水工况下，对单壁钢围堰的质量、安全和成本管控就显得尤为重要。

一般来说，围堰这一临时性结构面临着施工环境复杂、不确定性等问题[5]。因此，国内外许多学者对特定工况下围堰的安全性、施工工艺流程、结构优化设计等方面进行了大量研究。遆子龙等[6]基于三维绕射理论模拟钢围堰表面所受波浪压力分布，对实测波浪压力峰值分布规律进行验证。郭智杰等[7]对围堰断面进行优化，建立断面优化模型，提高了围堰的稳定性。陈家海等[8]采用拉丁超立方抽样生成钢套箱结构计算参数，通过灰色关联分析，以钢套箱总重为目标，对构件尺寸进行优化设计研究；刘丹娜等[9]运用有限元对单壁有底钢套箱围堰侧壁各构件进行了拓扑优化，并成功应用于工程实际；王明慧等[10]考虑钢护筒不同位置的影响，通过设置栓钉连接件的方式，对双壁钢套箱围堰封底混凝土厚度进行了修正和优化；高文波等[11]对应用于深水桩基加固的单壁钢套箱进行结构设计，开发出模板化单壁钢围堰和抱箍式吊装装置，形成了应用于深水桩基的增大截面法加固施工工艺；肖世波[12]通过在钢套箱内设置限位装置，满足了防浪抗渗的要求。孙小力等[13]对单壁钢围堰的内支撑和侧壁砸箍数量、布置方式进行了研究，表示增加内支撑数量能有效减小围堰变形，增加其稳定性。然而，目前对钢套箱围堰的研究大都体现在结构受力这一单目标分析上，而忽略了经济性、安全性、稳定性等其他重要因素上的考虑。

鉴于此，本研究结合贵州省清水江白市库区某大桥2#桥墩加固工程实例进行相关计算。该桥作业区水深达30.5 m，加密内支撑与加劲肋对围堰整体刚度的提高有限，因而采用在封底混凝土基础上继续浇注填充混凝土的新工艺来增强围堰的整体刚度。通过将不同内支撑间距和混凝土厚度设置成混合型变量，并以材料费用、重量以及抗浮稳定性为目标，对抽水施工工艺流程进行粒子群算法优化，得出一组最优解。在节省材料、降低造价的前提下，有效地将施工过程中围堰最不利位置的应力变形控制在容许值范围内，对同类型结构的优化设计具有一定的参考和借鉴意义。

1 多目标优化模型

1.1 力学模型

贵州省清水江白市库区某大桥为预应力混凝土连续梁桥，桥长128 m，桥宽7.8 m，是出入白市水电站库区的关键路段，交通量大。主梁为4 m×30 m组合T梁，桥墩采用矩形实体重力板式墩。该桥2#桥墩经钻心取样检测，结果表明：2#墩大里程侧28～32 m节段内混凝土抗压强度仅19.5 MPa，32～35 m节段为27.97 MPa，不满足设计要求。该墩采用了扩大基础，分3级台阶，阶宽与竖高均为1 m，基底尺寸为10.5 m×8.5 m，第2级台阶顶面距水面30.5 m，属于深水基础[14]。为了更好地适应现有的基础条件，经方案比选后，决定采用单壁无底钢套箱围堰对2#桥墩进行加固。

单壁无底钢套箱围堰受自重荷载、静水压力、水浮力、风荷载、流水压力、波浪力以及流动混凝土对围堰面板的侧压力等作用效应。其中，静水压力和浮力在抽水工况下会产生较大变化，根据其变化规律，可大致分为两种工况：(1)围堰浇注完混凝土后，边抽水边搭设内支撑。(2)抽水完毕，边凿除填充混凝土边搭设内支撑，直至填充混凝土凿除完毕。围堰不同工况下的竖向受力情况见图1。

图1 围堰不同工况下的竖向受力情况

在第1工况下，钢套箱围堰内壁分布有加劲肋和连接件分割的槽口，使得钢套箱与混凝土之间黏结紧密。故可将钢围堰、填充混凝土以及封底混凝土作为整体，则其竖向受到无底钢套箱围堰的重力Gg、封底混凝土重力Gt、填充混凝土重力Ggt、强风化板岩基面对钢围堰的支撑力Fc、钢围堰承受的浮力Ff1以及填充混凝土顶面静水压合力Gs共同作用，其竖向受力分析见图1(a)。设抽水深度为h，围堰顶部超出水面高度为h0，则水的浮力标准值：

Ff1=γVω=γSh。

(1)

由竖向受力平衡可得：

Fc+Ff1=Gg+Gt+Ggt+Gs。

(2)

则Fc=Gg+Gt+Ggt+(H-h0-2h-x1-x2)γS，抽水深度h越大，越容易发生抗浮失稳。

如图1(a)所示，钢套箱围堰大体上可分为内空腔段，填充混凝土段和封底混凝土段3个部分。取单位板宽，抽水工况下围堰内空腔段静水压力增量分布见图2，其中，内支撑用链杆表示，填充混凝土对钢套箱的约束作用简化为固定约束。

图2 前后两次抽水工况下静水压合力及合力增量分布

连续抽水过程中，内空腔段前后两次抽水静水压合力增量呈梯形分布，可采用多个不同编号的表明效应单元逐级加载来模拟抽水工况下静水压力变化。前一次抽水深度hi处静水压为：

Pi=0。

(3)

后一次抽水深度hi+1处以及填充混凝土顶部的静水压均为：

Pi+1=γω(hi+1-hi)，

(4)

式中γω为水的相对密度。

如图1(b)所示，在第2工况下，填充混凝土凿除完毕，将钢围堰与封底混凝土视为整体，则该整体竖向受到无底钢套箱围堰的重力Gg、封底混凝土重力Gt、钢围堰承受的浮力Ff2以及封底混凝土与墩柱之间的握裹力Fm共同作用。当封底混凝土与墩柱间的握裹力失效时，围堰发生上浮失稳。

设抽水深度与凿除的填充混凝土厚度之和为h，发生上浮失稳时，Fc=0，钢围堰承受的浮力达到最大值，由竖向平衡方程可得：

Ffmax=Ff2=Gg+Gt+Fm。

(5)

此时，抗浮稳定系数达到最小值：

(6)

1.2 优化模型

(1)设计变量：同时以连续变化的封底混凝土厚度x1、填充混凝土厚度x2以及呈离散分布的内支撑间距Χ=[d1,d2,…,di,…,dn]作为混合型设计变量。

(2)状态变量：强度约束条件，按容许应力法，钢材应力σ≤[σ]，混凝土应力σc≤[fc]；刚度约束条件，围堰刚度主要由构件的挠度体现。主跨绝对挠度[δ]≤L/400，次跨挠度[δ]≤L/250，L为计算跨径长。围堰水平位移[υ]≤H/2 000，H为围堰高度。

(3)多目标函数

①总重量目标：假设存在一个过程变量C：

(7)

C0=E(C)=max{n∈Z|n≤C}，

(8)

式中，x1为封底混凝土厚度；m为不等间距内支撑的层数；di为不同内支撑间距；Z为整数。

可得围堰内支撑层数：

(9)

以围檩和内支撑最小质量为目标函数：

(10)

式中，λi为长度相同的同种型号钢材的根数；Wi为单位长度不同型号钢材的质量；Li为不同型号钢材的长度。

②工程成本目标

以最少材料费用为目标函数：

(11)

式中，x1为封底混凝土厚度；x2为填充混凝土厚度；S为封底混凝土或填充混凝土底面积；αi为单位体积不同强度等级混凝土的价格，C30，C20混凝土单价分别按340，227/(元·m-3)计算；βi为单位质量不同型号钢材的价格，平均价格按4.0 元·kg-1计算；Zi为围檩或内支撑的质量。

③风险损失目标

采用抗浮稳定系数，作为最大浮力致险指标：

(12)

1.3 求解算法

1.3.1 算法概述

采用粒子群优化算法(PSO)对单壁钢围堰进行优化，该算法是一种概率型的全局优化算法，它通过模仿鸟群或鱼群的航行和觅食行为，在整个搜索空间中进行迭代寻优，可以较好地处理离散型和连续型设计变量。在粒子群算法中，通过全局极值Gbest或个体极值Pbest传递信息给其他粒子，属于单向信息流动，具有良好的记忆功能，当前最优解信息影响着整个搜索更新方向。因此，粒子群算法拥有相对于其他全局搜索算法更快的收敛速度[15]，以及在不同条件和环境下良好的实用性和有效性。但是现有粒子群算法的数学理论基础还不够牢固，其算法的收敛性还需进一步讨论。对于可行设计，当粒子群算法收敛或者设置的优化次数达到最大值，即可得出变量空间范围内满足约束条件的目标函数最优解。考虑多目标函数问题时，粒子群算法一般通过取多目标函数的加权平均作为适应度函数。无量纲适应度函数为：

minF(x)=∑(Wif(x))/SFi，

(13)

式中,W为权重系数；SF为比例因子。

1.3.2 算法模型

假设一个种群有n个粒子，每个粒子代表一组设计变量，每组设计变量记录着粒子的位置信息。用D维列向量来表示，Χj=(xj1,xj2,xj3,…,xjd)T，每个粒子在不同迭代次数下又有相对应的速度，Vj=(νj1,νj2,νj3,…,νjd)T，其位置和速度均需满足：xmin,i≤xji≤xmax,iνmin,i≤νji≤νmax,i,1≤j≤d,1≤i≤n。

从本质上来说，粒子群算法是一种迭代算法，粒子每迭代一次，就计算出相应的适应度值。粒子群在每一次迭代过程中，粒子需要找到个体所经历的位置以及种群所有粒子中适应度值最优的位置，分别记为个体极值Pbest和全局极值Gbest。然后通过比较新粒子、个体极值以及全局极值位置代入计算的适应度值，对个体极值和全局极值位置进行更新，进而迭代计算出粒子群中每个粒子新的位置和速度[16]。

(14)

(15)

(16)

2 结构优化分析

2.1 参数标定

单壁无底钢套箱围堰由面板、加劲肋、连接件、围檩、内支撑、封底混凝土以及填充混凝土组成。围堰高31.5 m，每节段2.25 m，共计14节段。所加固2#墩柱为4.5 m×2.5 m矩形截面，为预留足够的施工场地，套箱内轮廓尺寸相比于墩柱尺寸，外扩了1.75 m。施工水位按设防水位300.5 m计算，每抽水或凿除填充混凝土di为一次计算工况。选取不同的封底混凝土厚度进行多次试算，当封底混凝土厚度为x1=3.15 m时，抗浮稳定系数kmin=P抗/P浮>1.3，满足抗浮稳定性要求[17-18]。将前5层不同内支撑间距d1，d2，d3，d4，d5，其余相同内支撑间距d6=d7=…=dn=x0以及填充混凝土厚度x2作为设计变量。质量和造价是呈正相关的目标变量，由试算结果，取权重系数比值为0.05，将质量和造价目标函数值化为同一数量级。

表1 围堰部分结构参数

根据《无缝钢管尺寸、外形、重量及允许偏差》(GB/T 17395—2008)和《热轧型钢》(GB/T 706—2008)可知钢管、槽钢的理论质量分别为：

W1=πρ(D-S)S/1 000=71.514 kg/m,

(17)

W2=0.007 85[hd+2t(b-d)+

0.349(R2-r2)]=25.777 kg/m。

(18)

由此计算得围檩、内支撑和混凝土质量目标函数以及按材料采购价格计算得材料费用目标函数分别为：

(19)

minM=3.85C+47.78x2+150.49，

(20)

minf(x)=1.92C+0.84x2+3.94。

(21)

2.2 优化过程及结果分析

采用Isight与ANSYS联合仿真，通过运行Windows批处理文件直接调用围堰命令流，进行粒子群算法的优化。优化过程中材料质量与费用随迭代次数变化见图3。通过粒子群算法进行100次迭代计算后，得出一组最优解。在变量寻优过程中，虽然局部变化较大，但是优化结果满足设计要求，这是混合型变量组的部分离散性所致，不影响最优解的出现。

图3 目标函数迭代寻优过程

在围堰抽水工况下，随着抽水深度的增加，静水压强会逐渐增大。同时，越靠近填充混凝土，受到的约束效应越强。所以在该过程中，会产生一个最不利截面位置。为了充分考虑内支撑间距对围堰最不利位置的影响，采用控制变量法，将等间距内支撑围堰作为优化前的对照组，参数设置详情见表2。在各抽水工况下，优化前后围堰整体最大应力和位移随内空腔高度变化曲线见图4。

图4 优化前后围堰空腔高度-位移/应力变化曲线

计算结果表明，优化前围堰对照组的整体最大应力为196.6 MPa，小于强度设计值215 MPa，最大水平位移，[υ]≤15.75 mm，满足围堰强度和刚度设计要求。位移和应力拟合曲线的最大值点分别为4.33 m，5.20 m，水面以下空腔段高度为12.95 m。当抽水至水位线以下空腔段的1/3处时，位移达到峰值，位移峰值发生在水位线以下空腔段3/5处。空腔高度-位移变化曲线的上升段较陡，少量抽水能够引起较大的位移变化，所以应在该阶段加密内支撑，以降低位移变化幅值。由图4 (b)可知，当抽水至水位线以下空腔段2/5处时，整体应力达到峰值，应力峰值发生在水位线以下空腔段3/5处。抽水完成后，开始边凿除混凝土边搭设内支撑，直至填充混凝土凿除完毕。在该过程中，随着各工况下混凝土的凿除，应力发生了重分布，填充混凝土段应力和位移不断增大，但由于填充混凝土相比于内支撑能够提供给围堰更强的约束作用，故整体最大应力和位移均依旧发生在空腔段。综上所述，当抽水至水位线以下空腔段1/3～2/5处时，围堰最不利位置出现，应力和位移峰值出现在水位线以下空腔段3/5处左右，应着重加密水位线以下空腔段1/3～2/5处的内支撑。另外，虽然填充混凝土段刚度大，内力变形较小，但考虑到混凝土凿除施工引起的振动效应，不利于围堰稳定，故填充混凝土段内支撑间距也不宜过大。

由表2可知，通过粒子群算法计算得出的最优组参数分布，与上述规律较为相符，证明了单壁钢围堰优化方法的有效性。优化后的围堰在各工况下位移峰值为10.274 mm，相比于设置等间距支撑的围堰，整体最大位移下降了7.39%，峰值位置沿水深方向下移。优化后应力峰值为209.488 MPa，低于设计强度值。优化后钢套箱围堰整体位移峰值和混凝土应力峰值分布形式见图5和图6。位移是深水围堰设计计算的主要控制指标，位移过大将直接导致围堰结构失稳。在最不利抽水工况下，通过加密内支撑优化围堰的同时，还可以通过改变截面惯性矩来加强内支撑抗侧移刚度。由图6可知，混凝土应力均低于设计强度值，其中，混凝土最大应力为σmax=7.21 MPa，发生在填充混凝土顶面处，小于C20混凝土轴心抗压强度设计值，fc=9.6 MPa。

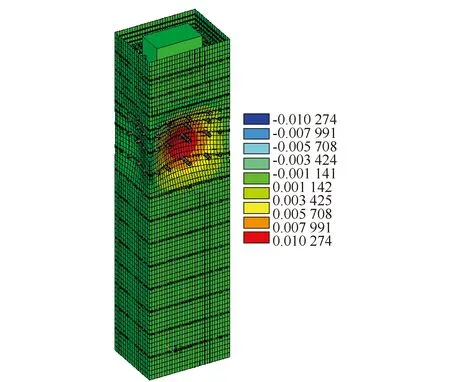
图5 优化后围堰位移峰值图(单位：m)

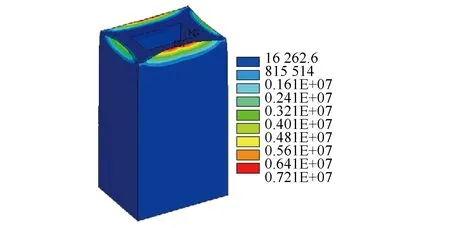
图6 优化后混凝土冯·米塞斯应力峰值图(单位:Pa)

表2 优化设计结果

3 结论

(1)根据深水区桥墩基础加固施工的主要特点，分析了钢套箱围堰的施工工艺流程，建立起两种典型工况下的力学模型，进而推导出最不利工况下围堰抗浮稳定系数的计算公式。

(2)深水单壁无底钢套箱围堰整体刚度主要受混凝土填充高度和内支撑间距的影响，且其最小抗浮稳定系数取决于封底混凝土质量。由此，本研究提出了一种围堰结构优化方法，即以材料费用、质量以及抗浮稳定系数为优化目标，通过改变封底混凝土的厚度进行多次试算，在保证抗浮稳定的前提下，调用粒子群算法进行优化，确定出一组最优的填充混凝土厚度与支撑间距，使得结构受力更加合理，在提高结构安全性的同时大大降低了工程造价，为深水区桥墩基础加固施工提供了参考与借鉴。

(3)通过采用多变量多约束多目标优化技术，对钢套箱围堰最不利受力变形位置出现的规律进行验证，同时避免了只考虑单一因素引起的局部优化，对指导实际加固工程施工更具有应用价值。