开链机械臂的反馈Hamel变分积分子*
2022-08-25沈伟清王本亮史东华
沈伟清 王本亮 史东华
(北京理工大学数学与统计学院,北京 100081)
引言
机械臂传统运动规划算法大致可分为路径规划和反应规划两种方式.路径规划通常由随机采样生成树、最优控制等方法得到可行或最优的避障路径,如Kuffner和La Valle等[1]提出的快速随机生成树法(Rapid Exploring Random Trees, RRT),Junge和Marsden等[2]提出的离散力学与最优控制方法(Discrete Mechanics and Optimal Control,DMOC),以及其他学者对上述方法一系列的改进,如RRT-connect,RRT,Batch Informed Trees等[3,4].这些算法用于机械臂路径规划时存在难以实时实现,计算复杂度高等缺陷.反应规划则通常由操作空间中引入的虚拟势场产生的力实现避障,如Khatib[5]提出的人工势场法,Chang和Marsden提出的回转力方法[6],以及改进的人工势场法[7]等.这些算法主要应用于移动机器人领域.
机械臂精确高效的反应规划往往要求解正向动力学问题.即在给定机械臂状态变量以及关节力或力矩的前提下确定其加速度[8].解此问题的多数方法使用Lagrange形式,并通过变分原理推导Euler-Lagrange方程,由给定初值的微分方程积分得到任意时刻的系统状态.在需长时间进行高精度控制机械臂场景中,其控制算法如何长时间保持系统守恒量,进而能定性准确地反应连续系统行为仍然是关键挑战.对于离散时间仿真,一些先进的微分方程数值算法也会因误差积累使系统产生耗散.为了解决这一问题,Kane等[9]说明了Newmark算法在某种意义上是离散力学的变分版本,可以保辛结构和动量,拥有较为出色的全局能量行为.Marsden和West[10]提出了变分积分子(VI),通过对 Lagrange函数离散变分得到的离散Euler-Lagrange(DEL)方程进行求解,构造了一种应用广泛的保辛算法.在此基础上出现的李群/李代数变分积分子已应用于诸多动力学建模与控制研究中[11-14].虽然基于DEL方程的变分积分子保辛,但仍然存在一定的计算复杂性.变分积分子将动力学方程的积分转化为代数方程组寻根,计算复杂性主要体现在计算DEL方程和雅可比逆矩阵两方面.在递归动力学的启发下,Lee等[15]提出了多体系统的一种李群变分积分子,将DEL的计算转化为求解离散逆动力学问题,并借助铰接体惯性算法(Articulated Body Inertial Algorithm,ABI)近似计算雅可比逆矩阵,得到了一种计算复杂度只有O(n)的算法.
通常情况下,机器人最显著的物理特征由几何来自然描述.Brockett[16]基于刚体运动的李群结构展示了如何用几何方式来描述运动链.关于用微分几何和李群语言研究机器人系统的表述参见文献[8,17].本文使用几何力学框架建立开链机械臂动力学模型并处理运动规划问题,建立了适用于开链机械臂多体系统的Hamel变分积分子,并引入反馈控制实现Hamel积分子寻根计算,使算法计算复杂度为O(n);此外将上述算法应用于反应规划的正向动力学计算,提出回转力与人工势场法的实时避障轨迹规划算法,可以克服传统人工势场法中易陷入势场局部极小的缺点.
本文其余部分安排如下:首先,利用旋量理论及指数积(Product of Exponentials,POE)公式,对开链机械臂正运动学建模,并在Lagrange力学框架下推导了其递归动力学及带反馈的Hamel变分积分子;其次,将回转力引入人工势场法中,通过回转力改进势场法中的斥力,实现机械臂整臂的实时避障轨迹规划;最后,通过两个数值仿真验证了上述所提算法的有效性.
1 基于POE公式的正运动学建模
本节给出机械臂正运动学建模方法.

2 开链机械臂的Hamel变分积分子
为模拟开链机械臂多体系统,本节给出开链机械臂的Hamel变分积分子,通过建立在每个杆上的活动标架描述运动,并采用变分原理推导开链机械臂Hamel方程,由此得出逆动力学方程.最后将上述过程离散化,将正向动力方程的积分问题转化为DEL方程的寻根问题,并将文献[14]中得到的开链机械臂Hamel变分积分子进一步简化更新,应用于冗余机械臂路径规划与反应规划中.
首先,我们通过Lagrange力学框架推导开链机械臂的递归动力学方程.考虑n连杆,关节位形θ=(θ1,…,θn) ∈ Tn.在第 i个杆的质心处建立随体标架{i},记gi-1,i∈ SE(3)为标架 {i}相对于标架{i-1}的位姿表示,g0,i简记为gi,则有


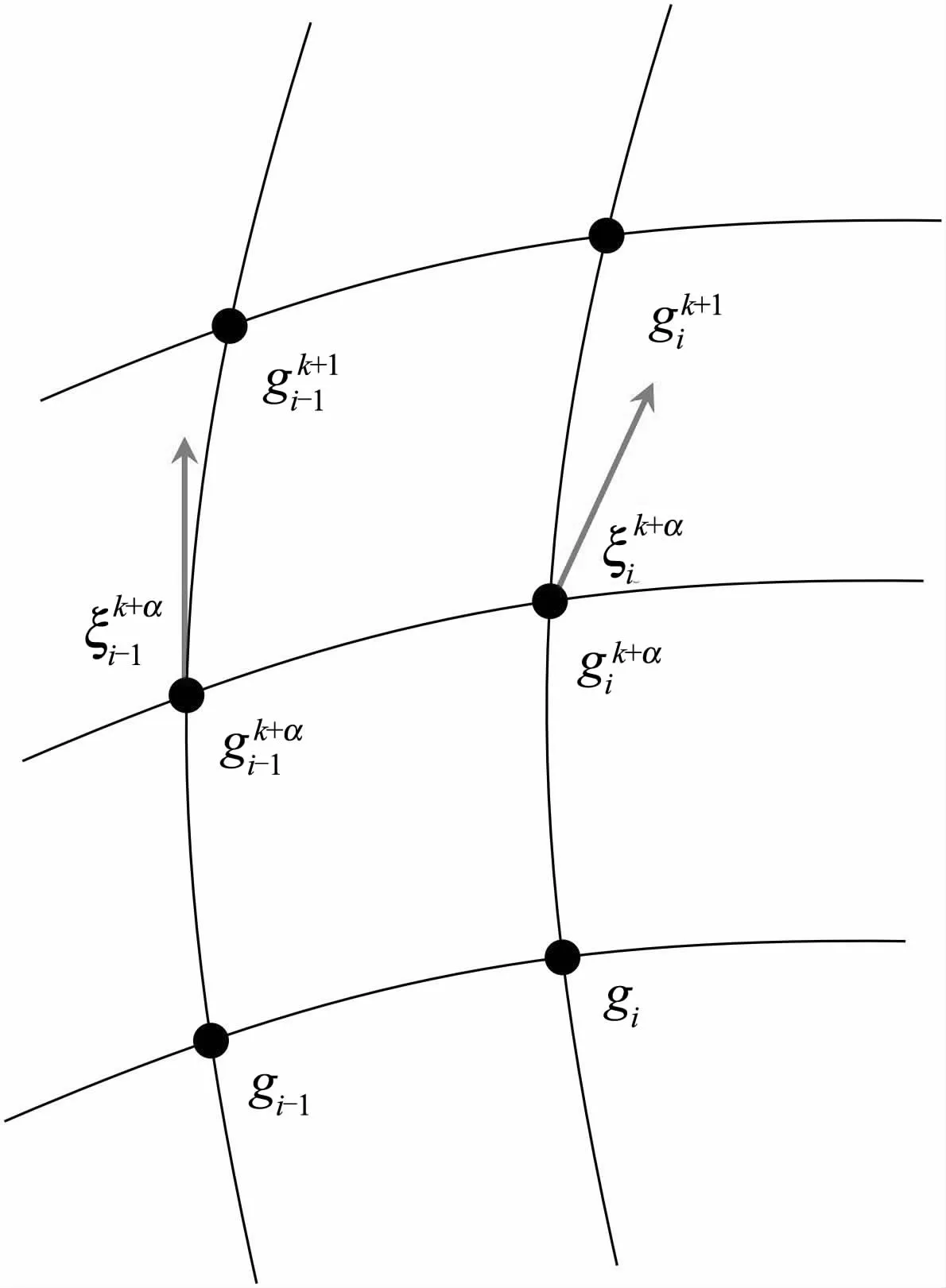
图1 离散积分子网格Fig.1 Discrete-time integrator grids


注 文献[14]已有上述定理类似的陈述和证明,本文利用引理1对其进行了更新和简化.
由此,我们给出开链机械臂的离散递归逆动力学算法Ⅰ.逆动力学方程一般用于最优控制问题中力矩约束的计算.

A l g o r i t h mⅠD i s c r e t e R e c u r s i v e I n v e r s e D y n a m i c s I n p u t: M a n i p u l a t o r p a r a m e t e r s S i,T st(0),I i,g i-1,i(0) a n d θ k,θ k+1,t i m e s t e p Δ t O u t p u t:m o m e n t τ 1:f o r i=1→ n d o 2:g k i-1,i=g k i-1,i(0)e A i θ k i 3: ξ k+α i=A d g-k i-1,i ξ k+α i-1+A i·θ k+1 i-θ k i 4:e n d f o r 5:f o r i=n→1 d o 6:f k i← b y f o r m u l a(1 3)7:τ k i← b y f o r m u l a(6)8:Δ t e n d f o r
3 Hamel方程寻根过程
本节我们通过反馈控制实现Hamel积分子的寻根计算.
DEL方程定义了系统的离散演化过程,若已知开链机械臂广义坐标为θk,为计算下一时刻满足约束流形(13)的解 θk+1,从控制观点看[15,19],可由DEL方程所得的 τe=h(qk,vk+1) (由算法 Ⅰ 定义)作为反馈控制引入机械臂运动方程,若‖τe‖小于某收敛阈值ε,则将θk+1视为下一时刻满足DEL方程的解,否则可利用τe构造迭代策略更新计算θk+1直到满足DEL方程.
机械臂封闭形式的动力学为
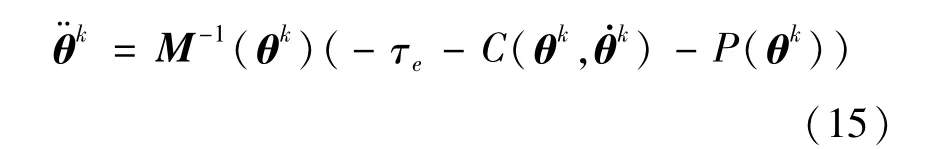

此迭代过程如图2所示.
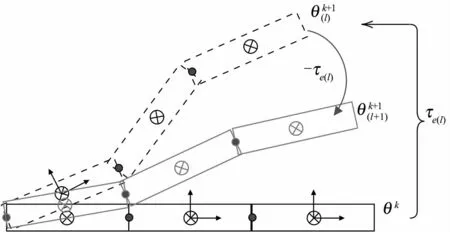
图 2 由反馈 τe(l) 进行迭代Fig.2 Iteration with feedback-τe(l)
4 回转力改进人工势场法
直接在关节空间中设计控制律并不直观.操作空间控制的思想是在需要执行任务的操作空间中设计控制律f,由雅可比矩阵将其转化为关节空间力矩τ.
由Khatib[5]提出的人工势场法常用于机器人操作空间中设计反应控制律,其关键在于将机器人放入一个虚拟的势场中,根据目标点产生的引力fatt和障碍物产生的斥力frep综合作用在机器人上实现避障目的.对机械臂而言,考虑机械臂末端位置为xe,目标点位置为 xd,kp,kv为控制系数,则施加在机械臂末端的引力取为

为简单起见,考虑球形障碍物O,当机械臂进入避障范围(|ρ|≤ρ0),假设机械臂连杆i距离障碍物最近一点为xi∈R3,则施加在连杆i上的斥力
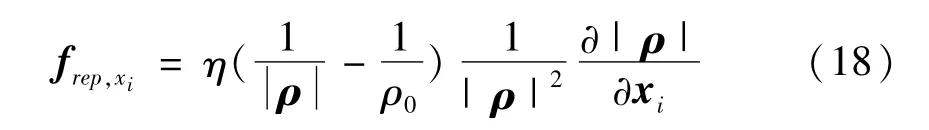
其中,η为增益项,ρ为xi指向障碍物最近点向量,ρ0为安全距离.
若目标点对机械臂的引力与障碍物对机械臂的斥力合力为0,那么机械臂将陷入人工势场法的局部极小点.我们提出一种改进策略如下:当机械臂进入避障范围(|ρ|≤ρ0)且ρ·>0,通过引入回转力取代式(18):

可将操作空间中的控制律转化为关节空间等效力矩,其中操作空间惯性矩阵,这里Jx为与f在同一个标架下描述的雅可比矩阵.下面给出改进人工势场法算法Ⅱ:

A l g o r i t h mⅡR e a c t i o n P l a n n i n g I n p u t: M a n i p u l a t o r p a r a m e t e r s S i,θ i,T st(0),I i,g i-1,i(0) ,O b s t a-c l e a v o i d a n c e c o e f f i c i e n t k p,k v,ρ 0,k obs a n d T a r g e t p o i n t x d 1:w h i l e M a n i p u l a t o r e n d-e f f e c t o r p o s i t i o n x e h a s n o t a r r i v e d x d d o 2: τ att=J T xe M xe[-k p(x e-x d)-k v ˙ x e],τ rep=0 3: i f|ρ|≤ρ 0 a n d ρ·˙ x i>0 4: c a l c u l a t e f*rep,xi b y f o r m u l a(2 0)5: τ rep=∑n J T x i M x i f*r e p,x i,τ a t t=0 6: τ=τ att+τ rep 7:i=1 e n d w h i l e
5 数值计算与分析
本节我们通过平面三连杆正向动力学和四连杆反应规划两个例子验证所提算法.
5.1 正向动力学
考虑除重力作用外不施加额外力矩的平面三连杆,其各关节为旋转关节,每根杆杆长为0.1m,质心取在各杆的几何中心,惯性矩阵Ii=diag(1,1,1,1,1,1),i=1,2,3.初始位形 θ=(0,0,0)T,重力矢量 e3=[0,0, -9.81,0]T,时间步长 Δt=0.01s.将标架取在关节质心处描述动力学,采用Hamel变分积分子,式(16)中初值取为 θk,ε取10-8,三连杆运动100s中各时间步寻根迭代次数及反馈误差力矩 τe分别如图5(a)和图5(b)所示,由其可见:Hamel积分子寻根计算迭代数小于等于4,且τe一直保持在10-8数量级范围内.三连杆质心轨迹见图3,末端y轴轨迹如图4所示,结果表明反馈Hamel变分积分子与作为基准算法的半隐式欧拉法[8]所得轨迹轨迹基本一致.

图3 三连杆各杆质心轨迹Fig.3 The trajectory of the center of mass of each link of the three-link manipulator

图4 三连杆末端y轴轨迹对比Fig.4 Comparison of y position at end-effector of the three-link manipulator

图5 Hamel积分子寻根计算迭代次数及反馈误差力矩τeFig.5 The number of iterations of the root-finding of Hamel's integrators and feedback error τe
5.2 改进人工势场法
考虑基本参数如表1所示的平面四连杆,第i杆的旋量轴Si:

表1 平面四连杆旋量参数Table 1 The screw axes and inertia matrix of the planar four-link manipulator

其中,ωi为旋转轴,qi和ci分别为关节i及质心i的位置向量.
平面四连杆初始位姿为

将标架取在关节质心ci处描述机械臂动力学,考虑平面四连杆整臂反应规划,用算法Ⅱ 所得仿真结果如图6所示.其中位置为(2.4,2.2,0)、半径为0.25的内侧圆圈表示障碍物,半径为0.75的外侧虚线圆圈外表示避障的安全区域,位置(2,3,0)的小圆圈表示目标吸引点,曲线为四连杆末端轨迹.当平面四连杆靠近障碍物时,由于传统人工势场法中目标点产生的吸引力和障碍物产生的斥力平衡而使平面四连杆陷入静止.经回转力改进,可使四连杆运动方向偏离障碍物而顺利避障,其轨迹如图6所示.结果表明相比于式(18)中的斥力形式,式(19)在一定程度上可以克服机械臂陷于势场局部极小的缺点.

图6 四连杆避障Fig.6 Avoidance of planar four-link manipulator
6 总结与展望
本文在Lagrange力学框架下推导了机械臂的递归动力学及带反馈的Hamel变分积分子,并将回转力引入传统人工势场法中改进斥力设计方式,实现机械臂整臂的实时避障轨迹规划.下一步将探究Hamel变分积分子保动量、保能量等保结构性质,并进一步构造多体系统的Hamel场变分积分子,利用场积分子分布式计算特征得到可用于实时并行计算的反应规划算法.
